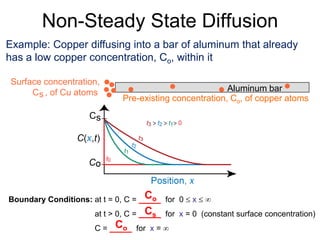
This document discusses diffusion, including: 1) Steady-state diffusion is when the rate of diffusion is independent of time and follows Fick's first law. Non-steady state diffusion follows Fick's second law, where concentration depends on both position and time. 2) The diffusion coefficient D increases exponentially with temperature and can be calculated from an Arrhenius equation. 3) Examples are provided to demonstrate calculating D at different temperatures and solving diffusion problems involving concentration gradients over time.

1. Before class, pass out photocopy of Callister Tables 5.1 and 5.2EM321: Lesson 8aChapter 5.4-5.5: Diffusion (part 2)

2. Review from Last Timeincreasing elapsed timeTypes of diffusionInterstitialVacancyExamples of diffusionRate of diffusion

3. Diffusion: Calculating FluxHow do we quantify the amount or rate of diffusion?J slopeM =massdiffusedtime

4. Steady-State Diffusion: Calculating FluxC1C1C2x1x2C2 xFor Steady-State Diffusion, the rate of diffusion is independent of timeFlux is proportional to concentration gradient =Fick’s first law of diffusionJ = fluxD = diffusion coefficient (Table 5.2)dC = change in concentrationdx = change in linear distance

5. Steady-State Diffusion and TimeDiffusion Coefficient, D, increases with increasing Temperature, TThe higher the Diffusion Coefficient, the more _______ atoms will diffuse across a given concentration gradient, such that:D1 t1 = D2 t2 Example: The diffusion coefficient for Copper in Aluminum is D = 4.15 * 10-14 m2/s at 500oC and D = 4.69 * 10-13 m2/s at 600oC. What time will be required at 600oC to produce the same diffusion result (in terms of concentration at a specific point) as for 10 hours at 500oC?quickly

6. Diffusion and Temperatureæ ö ç =DDoexpè ø QdD= diffusion coefficient [m2/s]-DoRT= pre-exponential [m2/s]Qd= activation energy [J/mol or eV/atom] R= gas constant [8.314 J/mol-K]T= absolute temperature [K]Diffusion Coefficient, D, increases with increasing T.

7. Diffusion and TemperatureT(C)1500100060030010-8D (m2/s)C in g-Fe C in a-FeD>> Dinterstitial substitutionalC in a-Fe Al in AlC in g-FeFe in a-Fe10-14Fe in g-FeFe in a-Fe Fe in g-Fe Al in Al10-201000K/T0.51.01.5D has an exponentialdependence on TFrom the graph of D vs. T, what can you conclude about Dinterstitial vs. Dsubstitutional?

8. transform dataln DDTemp = T1/TExample: Diffusion and TemperatureExample: At 300ºC the diffusion coefficient and activation energy for Cu in Si are D(300ºC) = 7.8 x 10-11 m2/sQd = 41.5 kJ/mol What is the diffusion coefficient at 350ºC?Note: You were not given thePre-Exponential, Do

9. T1 = 273 + 300 = 573KT2 = 273 + 350 = 623KD2 = 15.7 x 10-11 m2/sExample (cont.): Diffusion and Temperature

10. Another Example: Diffusion CoefficientExample: What is the Diffusion Coefficient, D, for theinterdiffusion of carbon in α-iron (BCC) at 900oC?(Note: Use data in Table 5.2 to find the Pre-Exponential, Do.)6.2 * 10-7From Table 5.2, Do = ________m2/s for carbon in α-FeQv = ____ kJ/mol = ___________ J/mol 8080,000Dα = 5.86  10-12 m2/s

11. Steady-State vs. Non-Steady StateUp until now, we have been looking at Steady-State diffusionWhat does “Steady-State” mean?- Concentration of diffusing species is a function of position only. Not a function of time (does not change over time). C = C(x)What do we do if our concentration gradient is “Non-SteadyState” (C is a function of both both position and time)?(e.g. when a material is first introduced to a concentration gradient and the impurity atoms begin to diffuse through it)- Use Fick’s Second Law (remainder of this lecture). Second order equation with C = C(x,t)

12. Non-Steady State DiffusionThe concentration of diffusing species is a function of both time and positionC = C(x,t)In this case Fick’s Second Law is usedFick’s Second Law

13. Non-Steady State DiffusionSurface concentration,Aluminum barCC, of Cu atomsssPre-existing concentration, Co, of copper atoms Example: Copper diffusing into a bar of aluminum that already has a low copper concentration, Co, within itCoBoundary Conditions:at t = 0, C = _____for 0  x   at t > 0, C = _____for x = 0 (constant surface concentration)C= _____for x = CsCo

14. Solution to Fick’s Second Law: CSC(x,t) = Conc. at point x at time terf (z) = error function erf(z) values are given in Table 5.1C(x,t)CoUsing Table 5.1:What value of z gives an error function of erf(z) = 0.4755?What value of z gives an error function of erf(z) = 0.9592?What value of z gives an error function of erf(z) = 0.3400?z = 0.45z = 1.45z = 0.3112

15. Example: Non-steady State Diffusion erf(z) = 0.8125Example: An FCC iron-carbon alloy initially containing 0.20 wt% C is carburized at an elevated temperature and in an atmosphere that gives a surface carbon concentration constant at 1.0 wt%. If after 49.5 h the concentration of carbon is 0.35 wt% at a position 4.0 mm below the surface, determine the temperature at which the treatment was carried out.Solution: uset = 49.5 h x = 4 x 10-3 m

16. Cx = 0.35 wt% Cs = 1.0 wt%

17. Co = 0.20 wt% Example (cont.): Non-steady State Diffusionzerf(z)0.90 0.7970z 0.81250.95 0.8209 Now solve for DWe must now determine from Table 5.1 the value of z for which the error function is 0.8125. An interpolation is necessary as followsz= 0.93

18. Example (cont.): Non-steady State Diffusionfrom Table 5.2, for diffusion of C in FCC FeDo = 2.3 x 10-5 m2/s Qd = 148,000 J/molT = 1300 K = 1027ºCTo solve for the temperature at which D has the above value, we use a rearranged form of the Diffusion Coefficient equation

19. Example: Chemical Protective ClothinggloveC1paintremoverskinC2x1x2Methylene chloride is a common ingredient of paint removers. Besides being an irritant, it also may be absorbed through skin. When using this paint remover, protective gloves should be worn.If butyl rubber gloves (0.04 cm thick) are used, what is the breakthrough time (tb), i.e., how long can the gloves be used before methylene chloride reaches the hand?Datadiffusion coefficient in butyl rubber: D = 110x10-8 cm2/sDiscussion Questions:How would you go about solving this problem? (Do not solve it.)Do you need to know the surface concentration of methylene chloride in order to solve this problem? Why or why not?