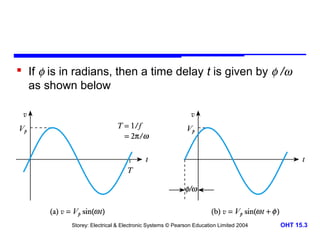
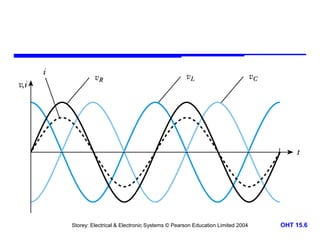
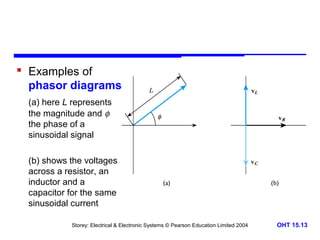
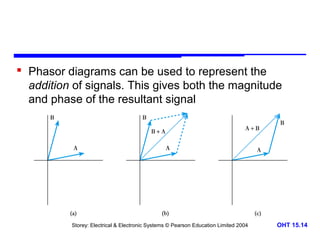
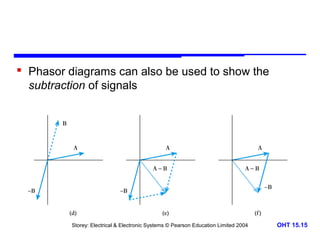
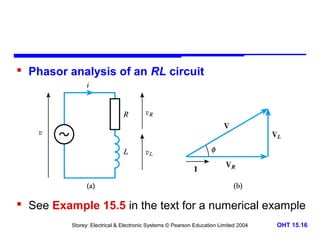
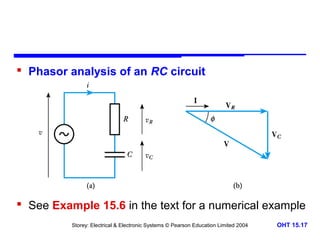
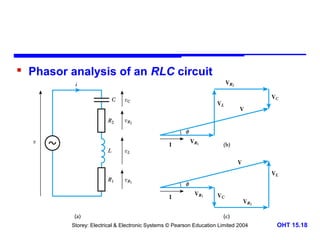
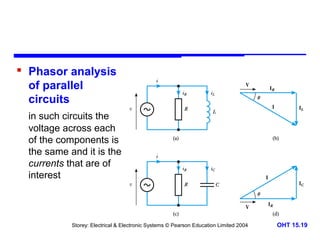
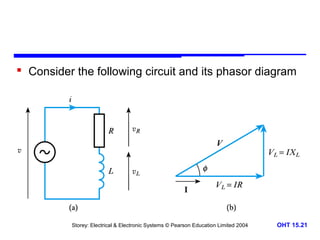
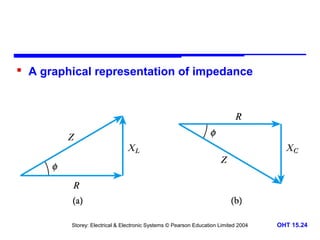
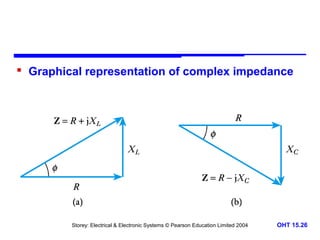
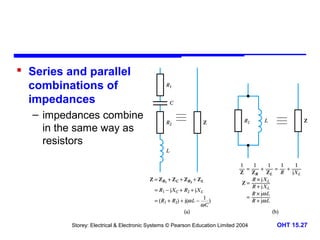
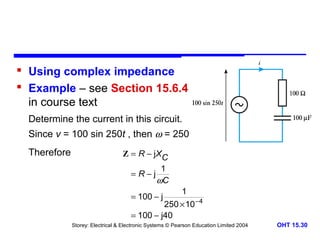
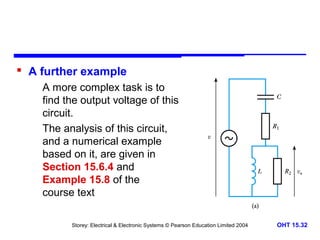
This document discusses alternating voltages and currents in electrical circuits. It introduces key concepts such as reactance of inductors and capacitors, phasor diagrams, impedance, and complex notation. Specific topics covered include defining sinusoidal voltages and currents, voltage-current relationships for resistors, inductors, and capacitors, defining reactance, using phasor diagrams to analyze circuits, defining impedance as the ratio of voltage to current in reactive circuits, and representing impedance using complex notation.