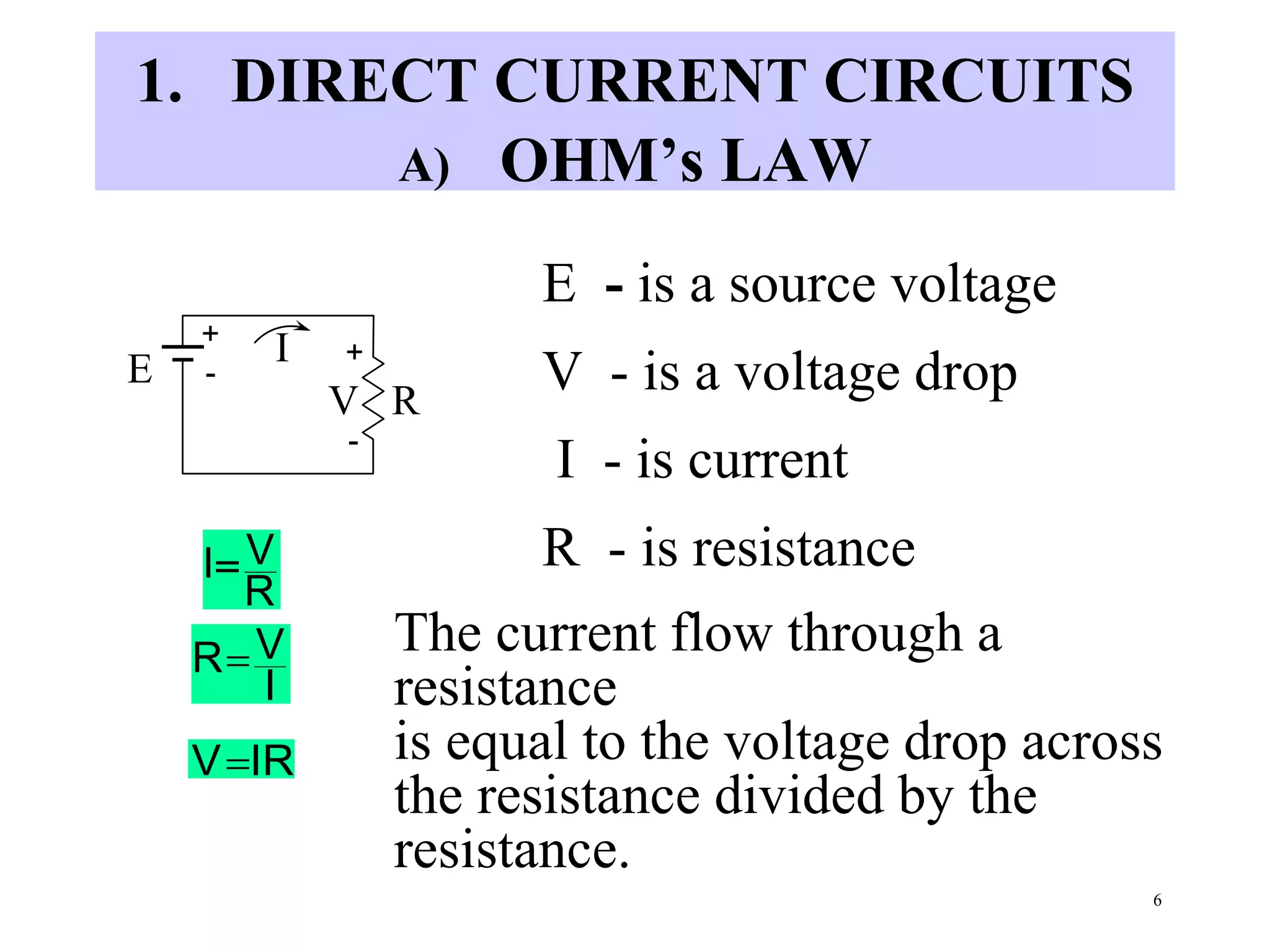
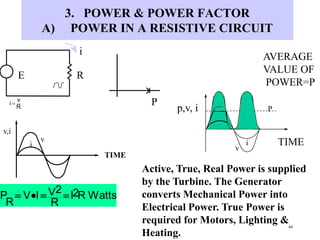
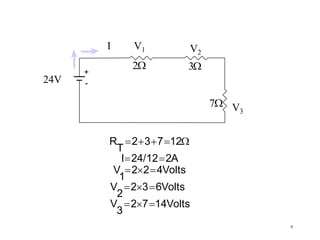
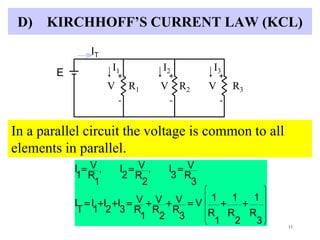
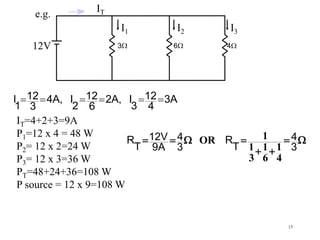
This document discusses direct current (DC) and alternating current (AC) circuits. It covers Ohm's law, power dissipation, Kirchhoff's laws, capacitive and inductive reactance, phasors, and RLC circuits. Key points include: - Ohm's law defines the relationship between current, voltage and resistance in a DC circuit. - Kirchhoff's laws allow analysis of voltage and current in series and parallel circuits. 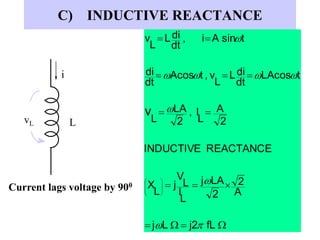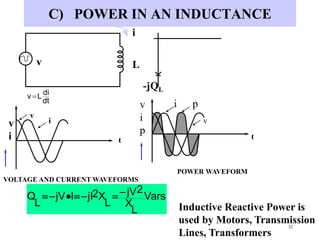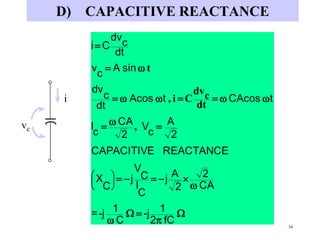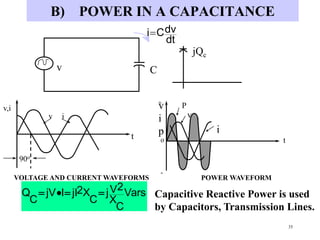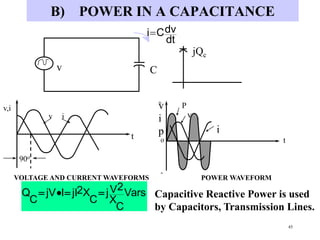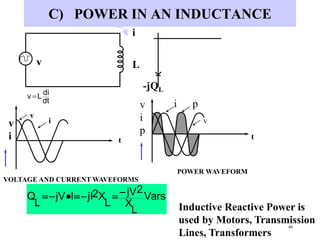- Inductive and capacitive reactance define how inductors and capacitors respectively impede alternating current in an AC circuit. 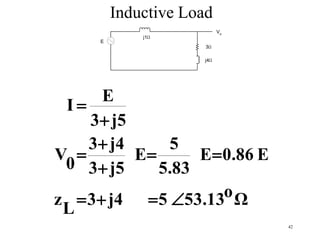- Phasors represent AC voltages and currents using complex numbers to facilitate circuit analysis. 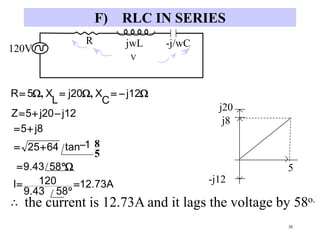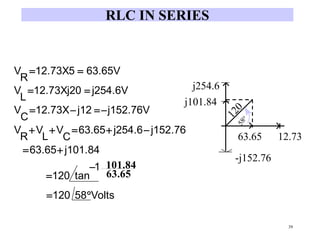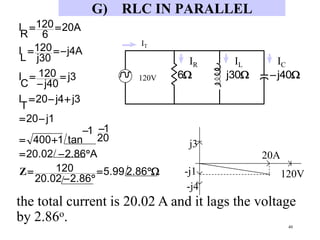- RLC circuits combine resistors,

1. 6
1. DIRECT CURRENT CIRCUITS
A) OHM’s LAW
+
-
-
+
E
I
V R
E - is a source voltage
V - is a voltage drop
I - is current
R - is resistance
The current flow through a
resistance
is equal to the voltage drop across
the resistance divided by the
resistance.
R
VI
I
VR
IRV

2. 7
B) POWER DISSIPATED IN A RESISTANCE
+
-
-
+
312V
e.g.
12V
Watts
Second
Joules
Second
Coulomb
Coulomb
JoulesVIP 
IRV
R2IIIRP  Watts
also I V
R

P V V
R
V
R
2
   Watts
4A
3
12I 
Watts48
3
212324412P 

3. March, 1998 (R-?)
vol10/auth/bb/intr/sf/22103/wc/electricity.ppt 8
C) KIRCHHOFF’S VOLTAGE LAW (KVL)
In a series circuit the
current is common to all
the elements in series.
KVL - The sum of the
voltage drops around a
closed electric circuit is
equal to the source
voltage.
+
-
+
-
+ - + -
+-
E
I
R1
R2
V3
E q u a t i o n
4
R
3
R
2
R
1
R
T
R
T
IR)
4
R
3
R
2
R
1
I(RE
4
IR
4
V,
3
IR
3
,V
2
IR
2
V,
1
IR
1
V
4
V
3
V
2
V
1
VE




V1
V2
V4
R4
R3

4. 9
I V1 V2
+
-24V
2 3
7 V3
Volts1472
3
V
Volts632
2
V
Volts422
1
V
A224/12I
12732
T
R






5. 10
Watts4828128
3
P
2
P
1
P
T
P
Watts28
2
7
14722142
3
P
Watts12
2
3
632262
2
P
Watts8
2
2
422242
1
P




P source = 24 X 2 = 48 Watts

6. 11
D) KIRCHHOFF’S CURRENT LAW (KCL)
+
-
+
-
+
-
IT
E
V R1 R2 R3
I1 I2 I3
V V
In a parallel circuit the voltage is common to all
elements in parallel.


















3
R
1
2
R
1
1
R
1
V
3
R
V
2
R
V
1
R
V
3
I
2
I
1
I
T
I
3
R
V
3
I,
2
R
V
2
I,
1
R
V
1
I

7. 12
KCL-The current flow towards a point is equal to
the current flow away from the point.
    R
T
V
I
T
1
R1
1
R2
1
R3
1
2 Resistors in Parallel
R1 R2
1

8. 13
IT
3A
4
12
3
I2A,
6
12
2
I4A,
3
12
1
I 
IT=4+2+3=9A
P1=12 x 4 = 48 W
P2= 12 x 2=24 W
P3= 12 x 3=36 W
PT=48+24+36=108 W
P source = 12 x 9=108 W



3
4
T
R
3
4
9A
12V
T
R
4
1
6
1
3
1
1OR
e.g.
12V
I1 I2 I3
3 6 4

9. 14
Current
(milliamps)
Effects
0 to 2 Threshold of sensation
3 to 8 Mild to painful sensation
9 to 19
Can not release grip due to muscular
contraction
20 to 69
Severe shock and risk of breathing
difficulties
Over 70 Risk of death from ventricular fibrillation
200
Risk of exit and entry point burns along
with severe burns to the skin
Source: Canadian Occupational Safety, January/February
1988
Effects of Electricity

10. 15
2. A.C. CIRCUITS
A) SINUSOIDAL VOLTAGE AND CURRENT
v +A
-A
t
SINE FUNCTION
A = AMPLITUDE
w = 2pf RADIANS/SECOND
v = A sin w t
0

11. 16
COSINE FUNCTION
v
-A
A
t v = A cos w t
t
v v=A sin w t v=A cos w t

12. 17
B) ROOT MEAN SQUARE (RMS) VALUE
The use of RMS values allows one to analyze an
A.C. circuit as if it were a D.C. circuit.
+
-
D.C. CIRCUIT A.C. CIRCUIT
I i
E V R v=f(t) v R

13. 18
T
P
P
V
t
P P
v
t
dt
R
2v
T
1avg
AC
Pavg
AC
P
DC
P
R
2v
AC
P
R
2V
DC
P
T



2
A
=wtsinAOFVALUERMSdt
2
v
T
1
=V
dt2v
T
12V,dt
R
2v
T
1
R
2V
T
TT





14. 19
MAGNETIC FLUX & INDUCTANCE
L - Henries
I - Amperes
N - Turns
 - Webers
The voltage induced in a coil is due to the time rate of change
of flux encircled by the coil. e = N * d /dt. But the flux is
produced by the current in the coil.
Therefore e = L*di/dt = N * d /dt or Li = N.
L = N / I

15. 20
Magnetic Flux In A Coil

16. 21
INDUCED VOLTAGE BY A MOVING
MAGNETIC FIELD

17. 22
VOLTAGE INDUCED IN A COIL

18. 23
TRANSFORMER ACTION

19. 24
MOTOR ACTION

20. 25
BASIC AC MOTOR

21. 26
INDUCED VOLTAGE IN A
ROTATING COIL

22. 27
INDUCED VOLTAGE IN A ROTATING COIL

23. 28
INDUCED VOLTAGE BY ROTATING FIELD

24. 29
3 PHASE AC GENERATOR

25. 30
AC GENERATOR WITH IMBEDDED WINDINGS
CLof Stator & Rotor
Voltage E being induced in
stator conductors
FluxRotor
Conductors
Rotor
Direction
of
Rotation
of
Rotor
F

26. 31
C) INDUCTIVE REACTANCE
i
vL L













fLj2Lj
A
2
2
LAj
L
I
L
V
j
L
X
REACTANCEINDUCTIVE
2
A
L
I,
2
LA
L
tLAcos
dt
diL
L
v,tAcos
dt
di
tsinAi,
dt
diL
L
v
v
pw
w
w
wwww
w
Current lags voltage by 900

27. 32
C) POWER IN AN INDUCTANCE
v L
i
v L di
dt

-jQL
v
i
v
i
VOLTAGE AND CURRENT WAVEFORMS
t
v
i
p
i p
v
POWER WAVEFORM
Vars
L
X
2jV
L
X2jIIjV
L
Q 
t
Inductive Reactive Power is
used by Motors, Transmission
Lines, Transformers

28. March, 1998 (R-?)
vol10/auth/bb/intr/sf/22103/wc/electricity.ppt 33
CAPACITOR

29. 34
D) CAPACITIVE REACTANCE
i
vc

p

w
w

w
wwww
w







,
dt
cdv
Ci,
t
fC2
1-j
C
1-j=
CA
2
2
Aj
C
I
C
V
j
C
X
REACTANCECAPACITIVE
2
A
c
V
2
CA
c
I
tCAcostAcos
dt
c
dv
sinA
c
v
dt
c
dv
Ci

30. 35
B) POWER IN A CAPACITANCE
v C
jQc
dt
dvCi
t
v,i
v i
90o
VOLTAGE AND CURRENT WAVEFORMS
o t
POWER WAVEFORM
+
-
v
i
p
P
v
i
Vars
C
X
2Vj
C
X2jIIjV
C
Q  Capacitive Reactive Power is used
by Capacitors, Transmission Lines.

31. 36
E) PHASORS
PHASORS ARE OF THE FORM a+jb
+j
(a+jb)
(a-jb)-j
a
a + jb represents the
addition of two vectors at
right angles.
2b2ajba  The angle that a + jb is tan-1
a
b
2b2ajba  tan-1
a
b
similarly 2b2ajb-a  tan -1
a
b-

32. March, 1998 (R-?)
vol10/auth/bb/intr/sf/22103/wc/electricity.ppt 37
When solving for currents and voltages in A.C.
circuits use is made of complex numbers.
When a resistance is added to a reactance the resultant
is called impedance.
(3+j4)
e.g.




53.13
,
5
2423
j43
L
XR
j4
L
X3R
tan -1 3
4

33. 38
F) RLC IN SERIES
120V
R jwL
V
-j/wC
-j12
j20
j8
5









5
8
,,
12.73A
589.43
120I
589.43
1tan6425
j85
j12j205Z
j12
C
Xj20
L
X5R
the current is 12.73A and it lags the voltage by 58o.

34. 39
RLC IN SERIES
Volts58120
1
tan120
j101.8463.65
j152.76j254.663.65
C
V
L
V
R
V
j152.76Vj1212.73X
C
V
j254.6V12.73Xj20
L
V
63.65V12.73X5
R
V








63.65
101.84
j254.6
j101.84
-j152.76
63.65 12.73

35. 40
G) RLC IN PARALLEL
IT
IR IL IC
120V  j40j306
j3
-j4
20A
120V












2.865.99
2.8620.02
120
A2.8620.02
20
11
tan1400
j120
j3j420
T
I
j3
j40
120
C
I
j4A
j30
120
L
I
20A
6
120
R
I
Z
the total current is 20.02 A and it lags the voltage
by 2.86o.
-j1

36. 41
Resistive Load
Vo
E
j1
I
5
E0.98
o11.315.1
E5
E
j15
5
I5
0
V
j15
E
I








37. 42
Inductive Load
Vo
E
j1
j4
3
Ωo53.135j43
L
z
E0.86E
5.83
5
E
j53
j43
0
V
j53
E
I








38. 43
Capacitive Load
j1
3
-j4
Vo
E
o53.135
j43
L
z
E18.1E
4.24
5
E
j33
j43
0
V
3j3
E
I









39. 44
3. POWER & POWER FACTOR
A) POWER IN A RESISTIVE CIRCUIT
E R
i
i
v
R
 P
v,i
i
v
TIME
p,v, i P
TIMEv
i
AVERAGE
VALUE OF
POWER=P
WattsR2I
R
2VIV
R
P 
Active, True, Real Power is supplied
by the Turbine. The Generator
converts Mechanical Power into
Electrical Power. True Power is
required for Motors, Lighting &
Heating.

40. 45
B) POWER IN A CAPACITANCE
v C
jQc
dt
dvCi
t
v,i
v i
90o
VOLTAGE AND CURRENT WAVEFORMS
o t
POWER WAVEFORM
+
-
v
i
p
P
v
i
Vars
C
X
2Vj
C
X2jIIjV
C
Q  Capacitive Reactive Power is used
by Capacitors, Transmission Lines.

41. 46
C) POWER IN AN INDUCTANCE
v L
i
v L di
dt

-jQL
v
i
v
i
VOLTAGE AND CURRENT WAVEFORMS
t
v
i
p
i p
v
POWER WAVEFORM
Vars
L
X
2jV
L
X2jIIjV
L
Q 
t
Inductive Reactive Power is
used by Motors, Transmission
Lines, Transformers

42. 47
D) POWER IN RESISTANCE & REACTANCE
VOLTAGE AND CURRENT WAVEFORMS
v
i
t
v
i
POWER WAVEFORM
v,i,p
v
i p
t

43. 48
-jQL
P
VA2Q2PZ2I
Z
2VIVU
VarssinZ2Isin
Z
2VsinIVQ
WATTScosZ2Icos
Z
2VcosIVP




44. 49
4. THREE PHASE STAR CONNECTION
A) CURRENT IN STAR CONNECTION
RED PHASE
CURRENT IR RED PHASE
WINDING
R
IR
RED PHASE
WHITE PHASEWHITE PHASE
WHITE PHASE
CURRENT IW
BLUE PHASE
R
BLUE
PHASE IB
BLUE PHASE
CURRENT
IB IW
R
3 PHASE GENERATOR OR SOURCE 3 PHASE LOAD







45. 50
WAVEFORMS OF BALANCED CURRENTS
+Im
-Im
-.5 Im
.866 Im
.5 Im
.866Im
iR iW iB
t
t1 t2 t3

46. 51
RED
PHASE
WHITE
PHASE
NEUTRAL
WIRE
BLUE
PHASE
R1 R2 R3
iR=Imax
iW=.5 Imax
iB=.5 Imax
iN=-IR +.5 Iw+.5 IB
STAR SOURCE USING 4 WIRES TO SUPPLY A
BALANCED THREE PHASE LOAD, AT TIME t1
IN= 0

47. 52
R
N
B W B W
N
RIR
R1
R2
R3
IB
IW
IR
IW
IB
LOAD


A) THREE PHASE 3 WIRE STAR SYSTEM

ILINE = IPHASE
SOURCE

48. 53
B) VOLTAGES IN STAR CIRCUITS
V = VNR
N
V = VNW
V = VNB
VBR=VLINE



= VNB -VNR
R
W
B

49. 54
VNR
-VNR
VNB
120o
30o
30o
haseV3VLine P

50. 55
5. THREE PHASE DELTA CONNECTION
A) CONNECTION
BLUE
PHASE
WHITE
PHASE
RED
PHASE
BLUE
PHASE
RED
PHASE
WHITE
PHASE
SOURCE LOAD

51. 56
B) WAVEFORM OF VOLTAGES GENERATED IN
THE DELTA CONNECTED WINDINGS
TIME
Vr Vw Vb
t1 t2

52. 57
C) PHASE AND LINE VOLTAGE
R
B
W
V PHASE
V PHASE
V PHASE
B R
W
V LINE
V LINE
V LINE
V PHASE =VLINE

53. 58
D) CURRENTS IN A DELTA SYSTEM
IB
IW
IR
R
W
B
W
B
R
SOURCE
LOAD
IR
IW
IB




54. 59
PHASE AND LINE CURRENTS IN A DELTA
-IW
IW
IR
-IR
IB
-IB
30o
30o
30o
IR
IB
IW






haseI3I pLine 

55. 60
6. POWER IN THREE PHASE CIRCUITS
A) POWER IN A STAR CONNECTION
2
T
Q2
T
P
T
U
V.A.
L
I
L
V3
T
U
Varssin
L
I
L
V3
T
Q
WATTScos
L
I
L
V3
T
Pcos
L
I.
3
L
V
3.
T
P
3
L
V
V,
L
II
cosI3V
T
PcosIVP














,
,
QT

PT
UT

56. 61
B) POWER IN A DELTA CONNECTION
V.A.
,.
I
,
2
T
Q2
T
P
L
I
L
.V3
T
U
Varssin
L
I
L
.V3
T
Q
WATTScos
L
I
L
V3
T
Pcos
3
L
I
L
3.V
T
P
3
L
I
cosI3V
T
PcosIVP












PT
UT
QT

57. 62
MACHINE INSULATION FAILURE
EXCESSIVE MOISTURE & HEAT
•MOISTURE WILL SEEP INTO THE HAIRLINE CRACKS OFAGING
INSULATION AND CREATE SHORT CIRCUIT BETWEEN WINDINGS
CAUSING SEVERE DAMAGE.
•TRANSFORMER OIL MUST BE KEPT DRY TO MAINTAIN ITS
INSULATION STRENGTH.
•PROLONGED HIGH TEMPERATURE OPERATION CAUSES
INSULATION TO BECOME BRITTLE AND CRACK & MOISTURE
PENETRATION RESULTS OR PHYSICAL CONTACT BETWEEN
CONDUCTORS.
•CHEMICALAGING OF OIL OCCURS RAPIDLY AT HIGH
TEMPERATURES. A DAILY RECORD OF THE OPERATING
TEMPERATURES IS MAINTAINED.