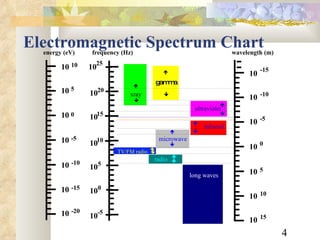
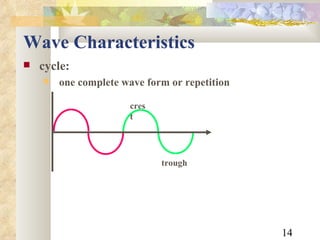
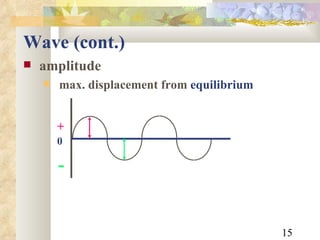
This document discusses electromagnetic radiation and its wave-particle duality. It covers key topics such as: 1) The electromagnetic spectrum ranges from radio waves to gamma rays, with different wavelengths and frequencies. Shorter wavelengths correspond to higher frequencies and energies. 2) Electromagnetic waves exhibit both wave and particle properties. The particle view is that radiation consists of discrete photon packets with energy directly proportional to frequency. 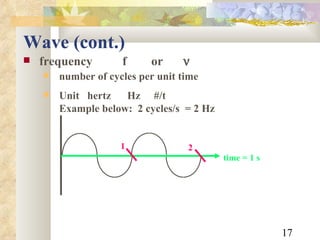3) Key relationships allow converting between wavelength, frequency, and photon energy, using constants like Planck's constant and the speed of light. Shortcut formulae allow quick calculation of photon wavelength from energy in keV or vice versa.

1. Physics Applied to Radiology Chapter 5

2. Electromagnetic Energy Spectrum continuous range of energy spectrum indicates that the distribution of energies exist in an uninterrupted band rather than at specified levels released by accelerating charged particles moves through space or matter as oscillating magnetic & electric fields needs no carrier medium but can have one can penetrate or interact with matter

3. Electromagnetic Spectrum transverse energy waves traveling as magnetic & electric fields  to each other maxima and minima of wave occur simultaneously unlike other waves, needs no carrier

4. Electromagnetic Spectrum Chart light

5. EMS Relationships Which of the following has the highest energy? Radio waves or visible light  frequency = 3.2x10 19 Hz or 4.9x10 14 Hz  wavelength = 8.5x10 -6 m or 4.2x10 -12 m 

6. EMS Relationships (cont.) Which of the following has the longest wavelength? microwave or ultraviolet waves  energy = 2.3x10 -5 eV or 57keV  frequency = 3.1x10 8 Hz or 8.9MHz 

7. EMS Relationships (cont.) Which of the following has the lowest frequency? Red light or yellow light  energy = 980 eV or 6.25x10 -2 keV  wavelength = 8325 mm or 4.78x10 -3 m 

8. General Characteristics of EMS no mass or physical form travel at speed of light ( c ) in a vacuum (or air) c = 3 x 10 8 m/s travel in a linear path (until interaction occurs) dual nature: wave vs. particle unaffected by electric or magnetic fields gravity

9. Characteristics (cont.) obeys the wave equation c =    obeys the inverse square law I 1 d 1 2 = I 2 d 2 2

10. EM Interactions with Matter sections may overlap general interactions with matter include scatter (w or w/o partial absorption) absorption (full attenuation)

11. EM Interactions (cont.)  probability if matter size  the wavelength examples: radiowaves vs. TV antena microwaves vs. food light vs. rods & cones in eye x rays vs. atom ionization occurs only EM energy > 33 to 35 eV high ultraviolet, x-ray, gamma

12. Dual Nature of EM Radiation continuously changing force fields energy travels as sine WAVE macroscopic level photon or quantum small bundle of energy acting as a PARTICLE microscopic level

13. PARTICLE vs. WAVE (in general) Wave extended in space always in motion repeating Particle (mass) localized in space moving or stationary

14. Wave Characteristics cycle: one complete wave form or repetition crest trough

15. Wave (cont.) amplitude max. displacement from equilibrium + - 0

16. Wave (cont.) wavelength  distance traveled by wave  = d/cycle Unit meter  m

17. Wave (cont.) frequency f or  number of cycles per unit time Unit hertz Hz #/t Example below: 2 cycles/s = 2 Hz time = 1 s 1 2

18. Wave (cont.) For the wave depicted below, determine the frequency and wavelength. t = 25 ms d = 58 nm cycles = 4.5 f = #/t = 4.5 cycles/25 ms = 4.5/25 x10 -3 = 180 Hz  = d/cycle = 58 nm/ 4.5 cyc. = 58 x 10 -9 /4.5 = 1.3 x 10 -8 m time = 25 ms d = 58 nm

19. Wave (cont.) velocity v (general) c (EM radiation) speed each cycle travels Unit m/s total distance wave moves in time period v of EM radiation always = c

20. Mathematical Relationships for EM Waves wave equation general: v =  f  or  v  EM radiation: c =  f  or c     constant velocity at c v = c = 3x10 8 m/s  of EM are inversely proportional       f    or vice versa 

21. Inversely Proportional as one goes up other goes down v =   f same    100 = 1 100 100 = 2 50 100 = 4 25 100 = 5 20 100 = 10 10

22. Example An x-ray photon has a wavelength of 2.1nm. What is its frequency? f    = 2.1x10 -9 m c = 3x10 8 m/s c =   f f  = c /  = [3x10 8 m/s] / [2.1x10 -9 m] = 1.428571428571 x 10 17 /s = 1.4 x 10 17 Hz

23. Example #2 A radio station broadcasts at 104.5 MHz. What Is the wavelength of the broadcast?  = ?? 104.5 x 10 6 /s =  [c = 3 x 10 8 m/s] c =  f     = c / f  = [3 x 10 8 m/s] / [104.5 x 10 6 /s] = 0.028708134 x 10 2 m = 2.871 m

24. Example #3 What it the frequency of microwave radiation that has a wavelength of 10 -4 m? f  = ?? 1 x 10 -4 m =   [c = 3 x 10 8 m/s] c =   f  = c /  = [3 x 10 8 m/s] / [1 x 10 -4 m ] = 3 x 10 12 Hz

25. Particle Nature (Quantum Physics) Photon (quantum) view as if a single unit of EM radiation indivisible Views EM radiation as a particle "bundle of energy" acts like a particle (but is not particle) relates E to  (direct relationship) "count" # of photons per unit time   f =  E

26. Mathematics E  f E = h f   h = Planck’s constant = 4.15 x 10 -15 eVs units usual energy units = J EM energy units = variation of J [eVs][/s] = eV x rays & gamma rays usually in keV or MeV

27. Example What is the energy (keV) of an x-ray photon with a frequency of 1.6 x 10 19 Hz? E = ?? 1.6x10 19 Hz = f [h = 4.15 x 10 -15 eVs] E = h f = [ 4.15 x 10 -15 eVs] [ 1.6 x 10 19 Hz] = 6.64 x 10 4 eV = [6.64 x 10 4 eV] / [10 3 ev / keV ] = 6.64 x10 1 keV = 66 keV

28. Example #2 What is the energy in MeV of an x-ray photon with a frequency of 2.85 x 10 21 Hz? E = ?? 2.85x10 21 Hz = f [h = 4.15 x 10 -15 eVs] E = h f = [4.15 x 10 -15 eVs] [2.85 x 10 21 Hz] = 11.8275 x 10 6 eV = [11.8275 x 10 6 eV] / [10 6 ev / MeV ] = 11.8 MeV

29. Wave & Particle Theories Combined    = inverse relationship   =   E &  = direct relationship   =  E E &  should have ??? . inverse relationship   =  E

30. Combination of Wave & Practical Theories combine formulas: c =    E = h   solve wave wave equation for frequency:  = c /   insert solution in quantum formula: [4.15 x 10 -15 eVs] [3 x 10 8 m/s]  m [12.4 x 10 -7 eVm]  m hc  m E eV =

31. Shortcut Formulae E eV = hc/  = [12.4x10 -7 eVm] /  m by incorporating changes in prefixes you can arrive at the following shortcut formulae: nm = 10 -9 m  [12.4 keV A]  A  E keV = A = 10 -10 m  [1.24 keVnm]  nm E keV =

32. Example What is the  of an 85 keV x-ray photon?  ?? 85 keV = energy need h & c E eV = hc  m  m = [4.15 x 10 -15 eVs] [3 x 10 8 m/s] E eV = [12.4x10 -7 eVm] 85 x 10 3 eV = 0.1458823529412 x 10 -10 m = .15 x 10 -10 m or .15A 

33. Shortcut method  ?? 85 keV = energy shortcut h & c E keV = 12.4 /  A  A = 12.4 / E keV = 12.4 / 85 = 0.1458823529412 = .15 A    E keV = 1.24 /  nm  nm = 1.24 / E keV =1.24/ 85 = 0.01458823529412 = .015 nm

34. Example #2 What is the energy of a .062nm x-ray photon? keV = ?? .062 nm =  nm shortcut h & c for nm E keV = 1.24 /  nm = 1.24 / .062 nm = 20 keV

35. Matter and Energy Relativity Formula Enables calculation of matter equivalence for any photon Must convert E in keV to E in J 1 J = 6.24x10 18 eV

36. Relativity problem example: What is the matter equivalence of a 86keV x-ray photon? ? = mass E = 86keV [c = 3x10 8 m/s]

37. Relativity problem example: How many electron-volts are contained in .25kg of matter? ? = E m = .25 kg [c = 3x10 8 m/s]