Tokyo.R #57 の発表資料です。

1. RとStanで
クラウドセットアップ時間を
分析してみたら
2016/9/24 Tokyo.R #57
中谷 秀洋(@shuyo, サイボウズ・ラボ)

2. MCMCサンプラー

3. いびつなサイコロの設計図
• 目が出る確率の分布を知りたい！
重心とか計算して
確率の理論値を求める？

4. 組み立てて、いっぱい投げる
１ ２ ３ ４ ５ ６

5. MCMCサンプラーとは
• サイコロの設計図（モデルファイル）を渡す
と、サイコロを作っていっぱい投げてくれる
data {
int<lower=0> N;
int<lower=0> M;
matrix<lower=0,upper=1>[N, M] z;
real<lower=0> jtime[N];
}
parameters {
real mu[M];
real<lower=0> sig[M];
matrix<lower=0>[N, M] y;
real c;
real<lower=0> s;
}
model {
for (n in 1:N) {
jtime[n] ~
normal(c + dot_product(y[n], z[n]), s);
for (m in 1:M) {
y[n, m] ~ lognormal(mu[m], sig[m]);
}
}
// 事前分布
for (m in 1:M) {
mu[m] ~ normal(0, 1);
sig[m] ~ gamma(1, 0.1);
}
c ~ normal(0, 1);
s ~ gamma(1, 1);
}
かなり複雑な
設計図でもOK!

6. Stan
• 代表的なMCMCサンプラーのひとつ
– 条件付き確率で記述されたモデルを MCMC
で解く
• 推定したい「値」は確率変数(ベイズ！)
– 点推定ではなく分布を推定
– 推定値が欲しいときは平均をとる
• というあたりを実例で説明

7. 参考文献
岩波データサイエンス vol.1 StanとRでベイズ統計モデリング

8. （サイボウズのサービスの説明が
少々続きますが
分析動機に関係するためであり
けっして宣伝ではありません）

9. サイボウズのクラウドって
申し込んだら
すぐ使えるんだって！（ステマ

10. cybozu.com のお試し/購入
はじめてcybozu.comを購入する | 購入方法 | サイボウズ製品サイト cybozu.com
https://www.cybozu.com/jp/buy/first/

11. 試用するサービスの選択
チェックを入れた
サービスが利用可能に

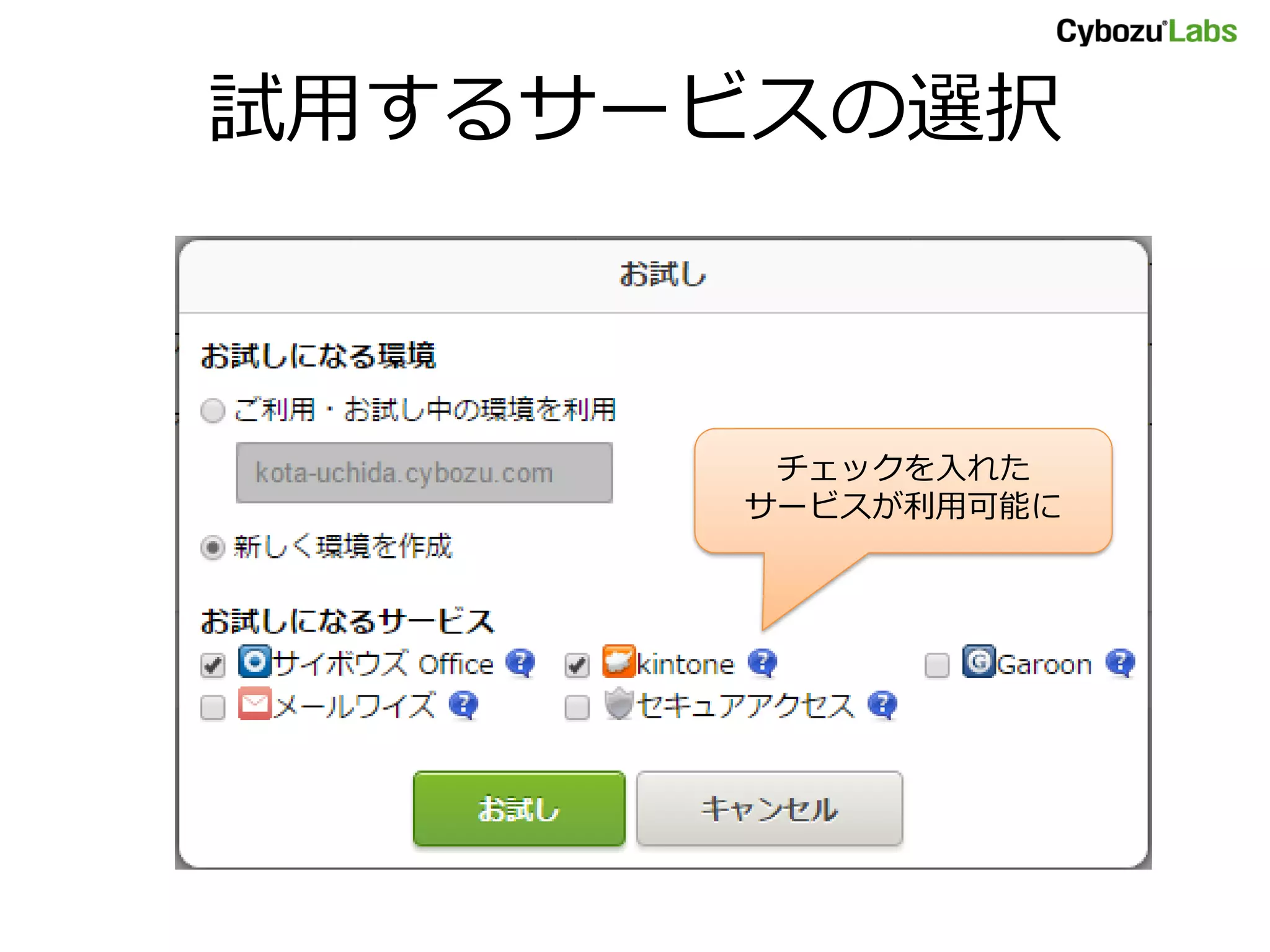
12. cybozu.com の 5つサービス
• kintone Webデータベース
• サイボウズ ガルーン (garoon)
• サイボウズ オフィス (office)
• メールワイズ (mailwise) メール共有
• セキュアアクセス (skylab)
グループウェア

13. セキュアアクセス(“skylab”)
• 安全な接続を提供するオプションサービス
– クライアント証明書によるアクセス制限
– https://www.cybozu.com/jp/service/option/
• 単機能のアプリケーション
– 規模は office などより かなり小さい
– skylab 単独で使用されることは基本ない

14. 申し込みから５分で使える
• 小人さん(という名の担当者)が24時間待機
• 申し込みの通知が来たら
• 急いでセットアップしてお客さんにメール
– なわけなく、自動化されている

15. “village” : 自動セットアップ
• 申し込まれたサービスを自動的にセット
アップする仕組み
– ７割のジョブは１分以内にセットアップ完了
– 99% は４分以内
– 0.25% が５分以上
• 「ご発注から5分～10分程度」と歌ってお
り、5分以内が望ましい

16. 何に時間がかかっている？
• village の履歴ログ(抜粋)
– jtime ＝そのセットアップジョブの合計実行時間(秒)
– kintone ～ skylab ＝各サービスがセットアップ対象(=1)
か、対象外(=0)か
• 分析すれば、各サービスごとのセットアップ時間がわ
かる？
> head(village)
jtime kintone garoon office mailwise skylab
1 3.6307 1 0 0 0 0
2 18.1070 0 0 0 1 0
3 13.5170 0 0 1 0 0
4 13.3591 1 0 0 0 1
5 8.7739 0 0 1 0 0
6 2.8032 1 0 0 0 0
kintone と skylab の
セットアップに
13.4秒かかった

17. R で分析

18. lm 関数で重回帰
> summary(lm(jtime~1+kintone+garoon+office+mailwise+skylab, data=village))
Call:
lm(formula = jtime ~ 1 + kintone + garoon + office + mailwise +
skylab, data = village)
Residuals:
Min 1Q Median 3Q Max
-21.525 -2.746 -1.746 2.254 86.841
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.2244 0.1172 36.04 <2e-16 ***
kintone 1.5214 0.1245 12.22 <2e-16 ***
garoon 31.1726 0.1518 205.32 <2e-16 ***
office 6.7723 0.1223 55.37 <2e-16 ***
mailwise 8.4679 0.1480 57.20 <2e-16 ***
skylab 5.3662 0.1781 30.13 <2e-16 ***

19. 分析完了
jtime = 4.2 + 1.5𝑧kintone + 31.2𝑧garoon +
6.8𝑧office + 8.5𝑧mailwise + 5.4𝑧skylab + 𝜖
– 𝑧サービス名はそのサービスを選択していれば 1、非選択なら 0
– office を選択すると6.8秒、skylab を選択すると 5.4秒追加される
• skylab のセットアップは office と同等の時間
– アプリ規模に比べて遅い。高速化はきっと容易だろう……
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.2244 0.1172 36.04 <2e-16 ***
kintone 1.5214 0.1245 12.22 <2e-16 ***
garoon 31.1726 0.1518 205.32 <2e-16 ***
office 6.7723 0.1223 55.37 <2e-16 ***
mailwise 8.4679 0.1480 57.20 <2e-16 ***
skylab 5.3662 0.1781 30.13 <2e-16 ***

20. 分析完了？
jtime = 4.2 + 1.5𝑧kintone + 31.2𝑧garoon +
6.8𝑧office + 8.5𝑧mailwise + 5.4𝑧skylab + 𝜖
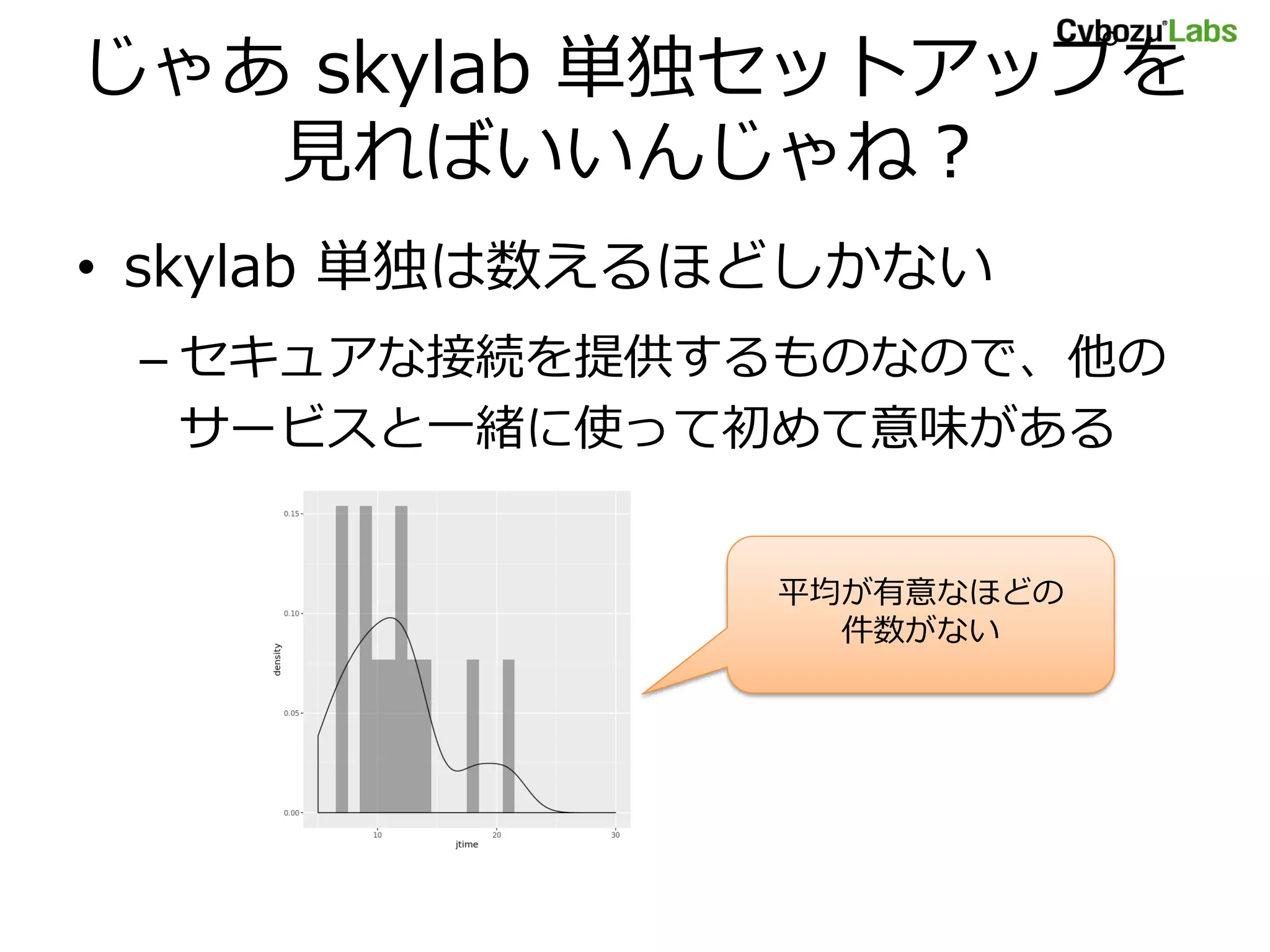
• skylab 遅すぎない？
– アプリの規模がぜんぜん違うのに……
• モデルに問題があるとすれば、
– 残差 𝜖 がサービスによらず共通
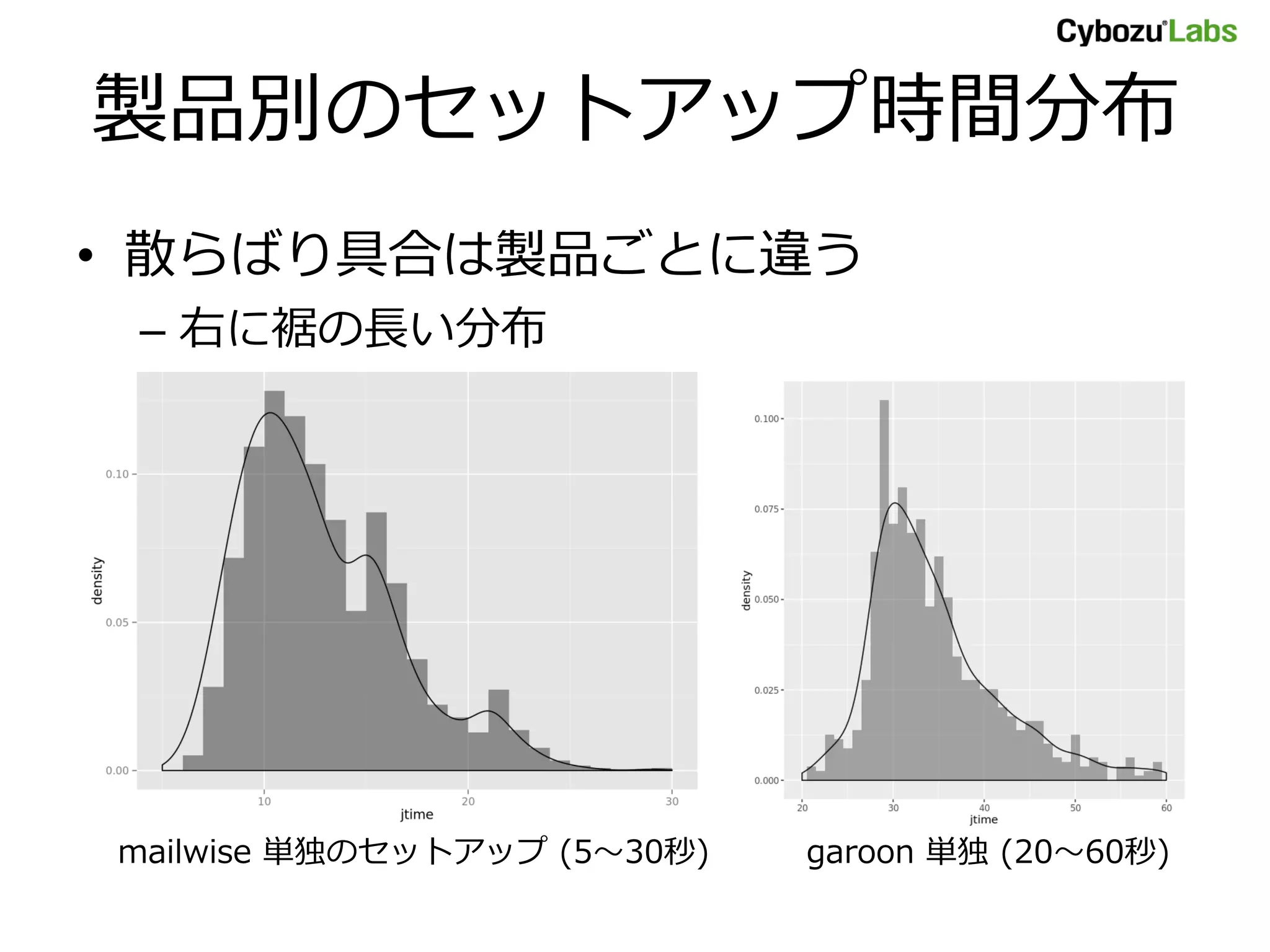
• garoon の分散 >>> office の分散 > kintone の分散
• garoon と一緒に選択されることが多い skylab が分散を吸収？
– 右に裾が長い分布なのに、考慮してない
• 残差 𝜖 が大きく負になると、jtime も負に！

21. モデルを改良しよう！

22. 製品別のセットアップ時間分布
• 散らばり具合は製品ごとに違う
– 右に裾の長い分布
mailwise 単独のセットアップ (5～30秒) garoon 単独 (20～60秒)

23. 対数正規分布
• 対数が正規分布に従う分布
– 右に裾が長い
– いい感じにフィッティング
jtime の対数の平均と標準
偏差をパラメータとする
対数正規分布でフィッティ
ング

24. じゃあ skylab 単独セットアップを
見ればいいんじゃね？
• skylab 単独は数えるほどしかない
– セキュアな接続を提供するものなので、他の
サービスと一緒に使って初めて意味がある
平均が有意なほどの
件数がない

25. 改良モデル
• 各サービスのセットアップ時間 𝑦 がそれ
ぞれの対数正規分布に従う
𝑦𝑛𝑚|𝜇 𝑚, 𝜎 𝑚 ~ ℒ𝒩(𝜇 𝑚, 𝜎 𝑚)
𝑦
𝑀
𝜇
𝜎
Log-Normal=対数正規分布
𝑚 =
𝑦 𝑚 =

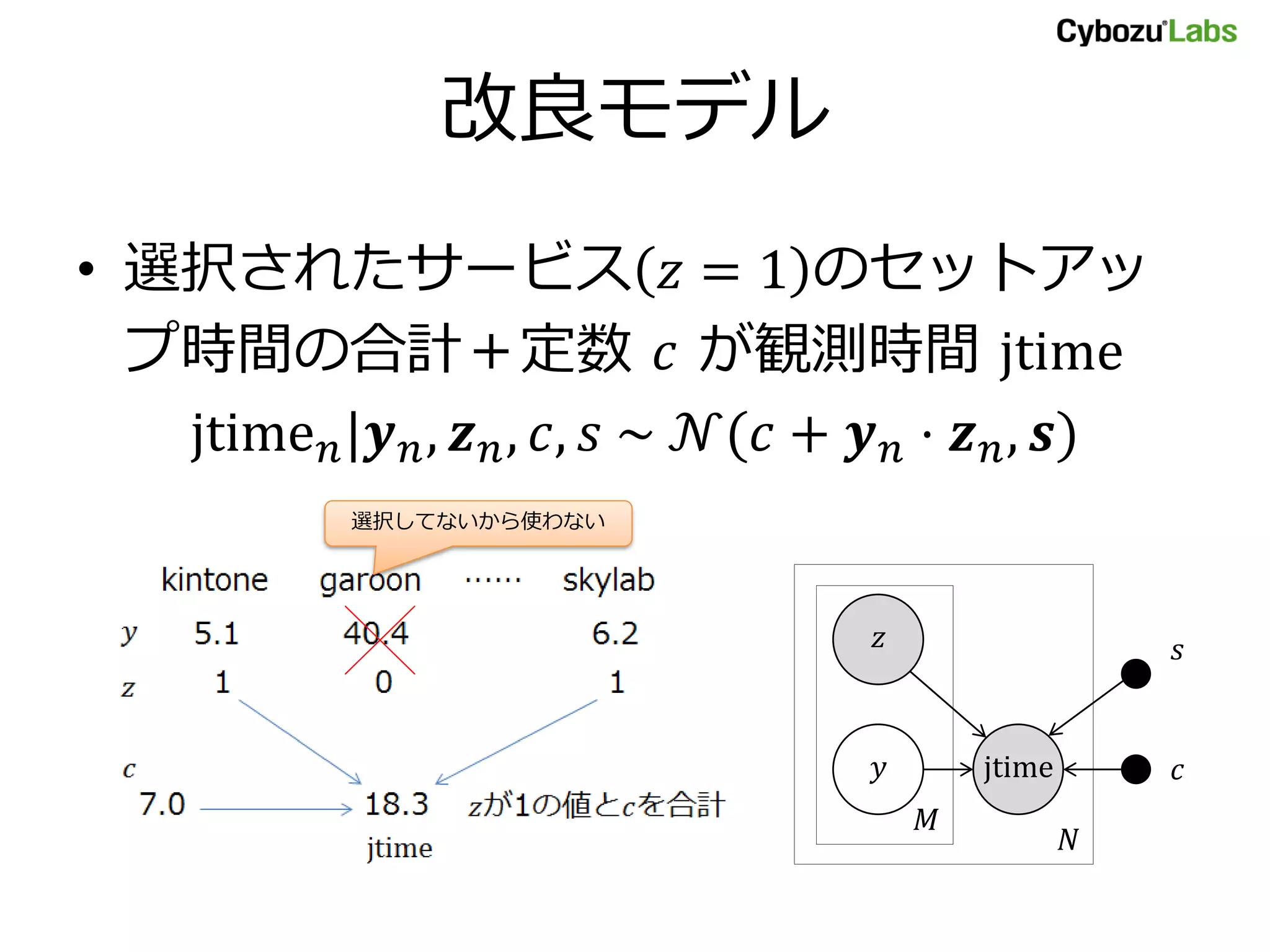
26. 改良モデル
• 選択されたサービス 𝑧 = 1 のセットアッ
プ時間の合計＋定数 𝑐 が観測時間 jtime
jtime 𝑛|𝒚 𝑛, 𝒛 𝑛, 𝑐, 𝑠 ~ 𝒩(𝑐 + 𝒚 𝑛 ⋅ 𝒛 𝑛, 𝒔)
𝑧
jtime𝑦
𝑁
𝑀
𝑠
𝑐
選択してないから使わない

27. 良さげなモデルができた！？

28. でも最尤法では解けない……
• 未観測変数 𝑦 を積分消去しないといけない
∫ 𝑃 jtime 𝑧, 𝑦 𝑃 𝑦; 𝜇, 𝜎 𝑑𝑦
• しかも 𝑦 は対数正規分布(←計算が難しいやつ)
𝑃 𝑦; 𝜇, 𝜎 =
1
2𝜋𝜎𝑦
exp −
ln 𝑦 − 𝜇 2
2𝜎2
未観測変数は
積分消去しないと
最尤推定できない

29. MCMC サンプラーなら
解けるよ！

30. Stan で分析

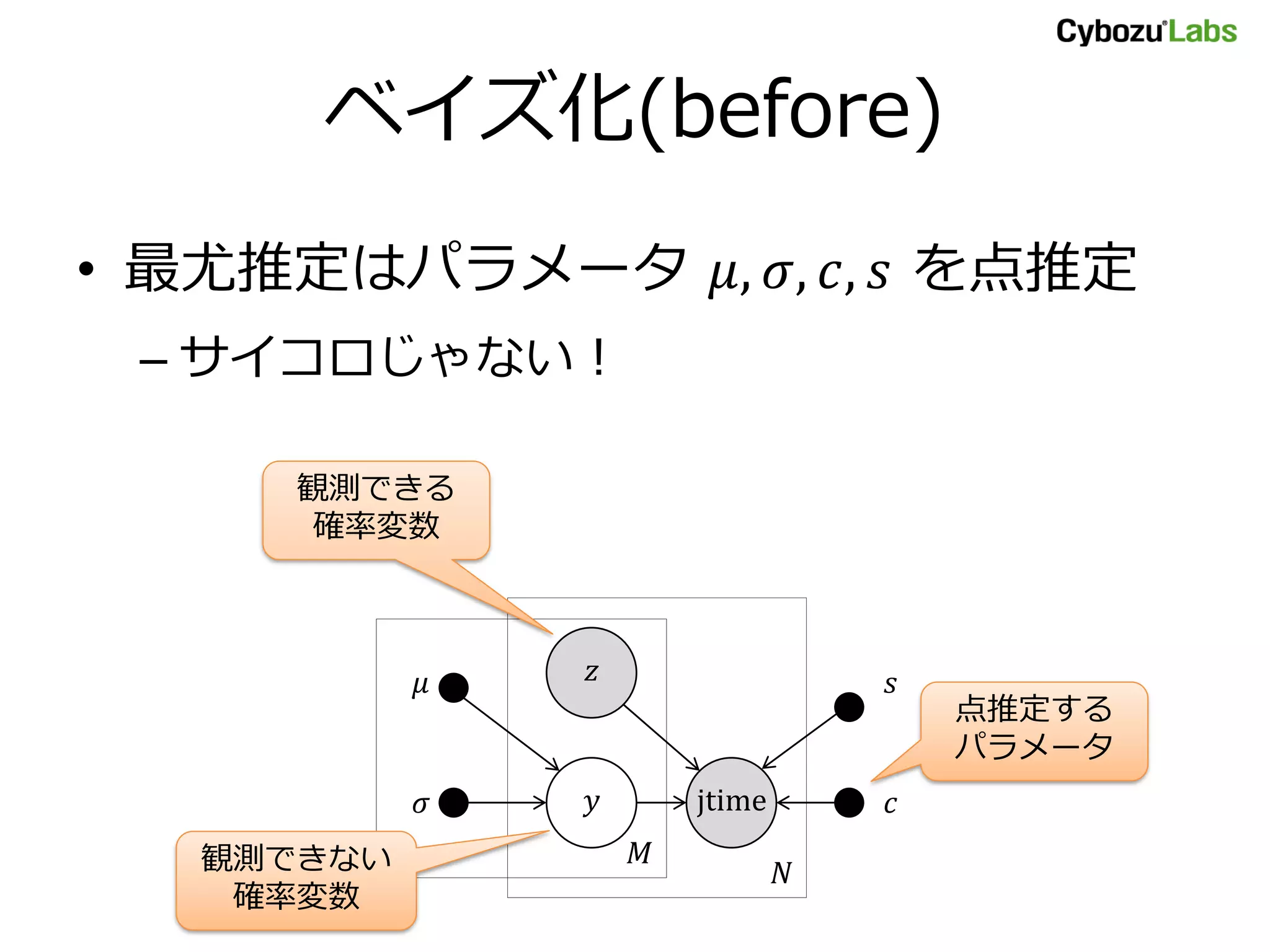
31. Stan に食わせるには……
• Stan は MCMC サンプラー
– サイコロをいっぱい振ってくれる奴
• 求めたい値がサイコロ(＝確率変数)になっ
てないと Stan に食わせられない
– ベイズ化≒パラメータを確率変数にすること

32. ベイズ化(before)
• 最尤推定はパラメータ 𝜇, 𝜎, 𝑐, 𝑠 を点推定
– サイコロじゃない！
𝑧
jtime𝑦
𝑁
𝑀
𝜇
𝜎
𝑠
𝑐
点推定する
パラメータ
観測できる
確率変数
観測できない
確率変数

33. ベイズ化(after)
• パラメータをサイコロ(確率変数)に
– 𝜇, 𝜎, 𝑐, 𝑠 が黒丸から大きい白丸に変わった！
𝑧
jtime𝑦
𝑁
𝑀
𝜎
𝜇
𝑐
𝑠
サイコロ振りの対象に
追加してしまおう！

34. 何が変わるの？
• 実はあんまり変わらない (違いは後ほど)
𝑦𝑛𝑚|𝜇 𝑚, 𝜎 𝑚~ℒ𝒩(𝜇 𝑚, 𝜎 𝑚)
jtime 𝑛|𝒚 𝑛, 𝒛 𝑛, 𝑐, 𝑠~𝒩(𝑐 + 𝒚 𝑛 ⋅ 𝒛 𝑛, 𝑠)
𝑧
jtime𝑦
𝑁
𝑀
𝜎
𝜇
𝑐
𝑠

35. Stan に渡す設計図を書こう
• モデルファイル
𝑧
jtime𝑦
𝑁
𝑀
𝜎
𝜇
𝑐
𝑠
data {
int<lower=0> N;
int<lower=0> M;
matrix<lower=0,upper=1>[N, M] z;
real<lower=0> jtime[N];
}
parameters {
real mu[M];
real<lower=0> sig[M];
matrix<lower=0>[N, M] y;
real c;
real<lower=0> s;
}

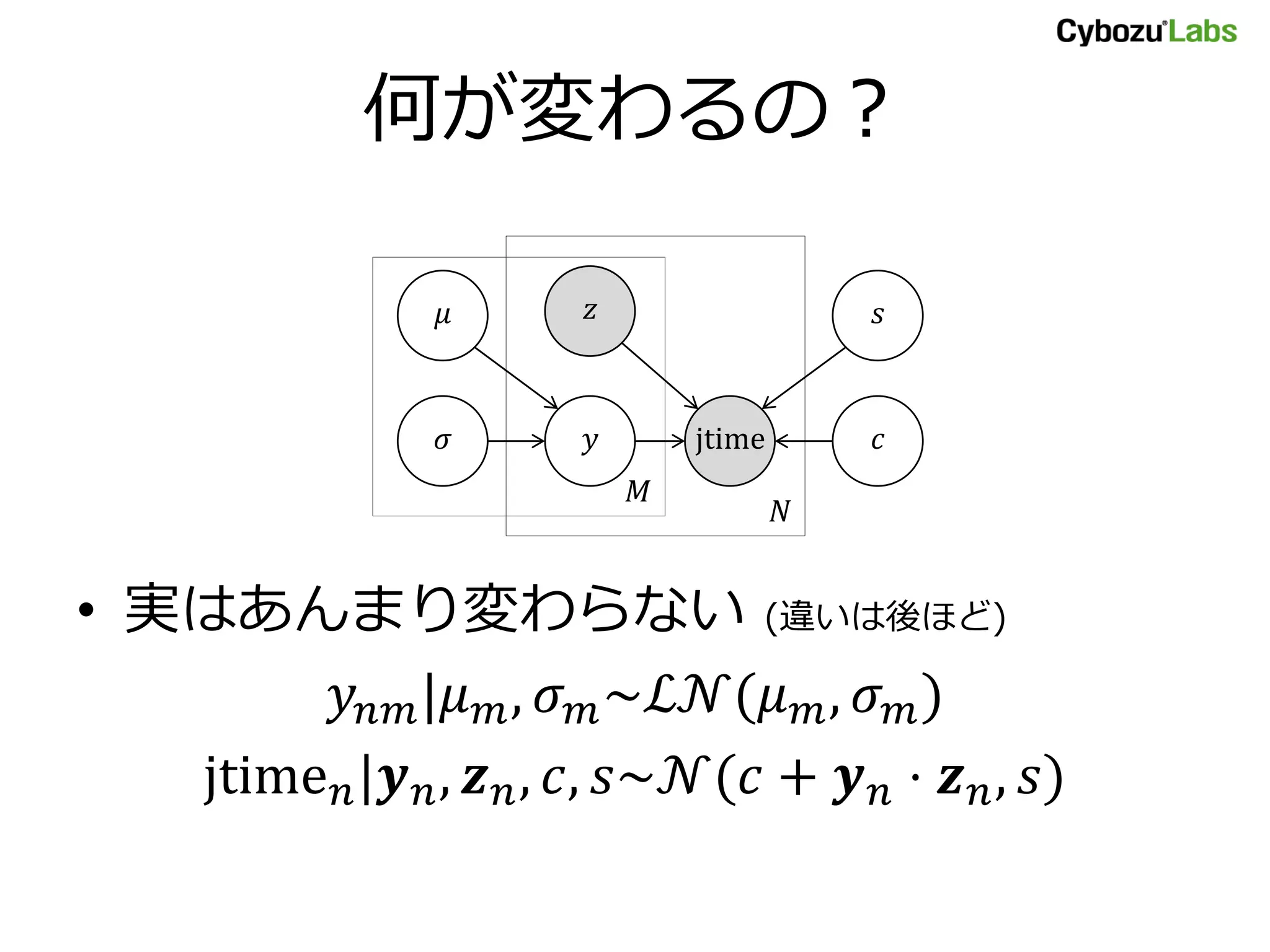
36. 条件付き分布
• (1) 𝑦𝑛𝑚|𝜇 𝑚, 𝜎 𝑚 ~ ℒ𝒩(𝜇 𝑚, 𝜎 𝑚)
• (2) jtime 𝑛|𝒚 𝑛, 𝒛 𝑛, 𝑐, 𝑠 ~ 𝒩(𝑐 + 𝒚 𝑛 ⋅ 𝒛 𝑛, 𝒔)
model {
for (n in 1:N) {
for (m in 1:M) {
y[n, m] ~ lognormal(mu[m], sig[m]); // (1)
}
// (2)
jtime[n] ~ normal(c + dot_product(y[n], z[n]), s);
}
}

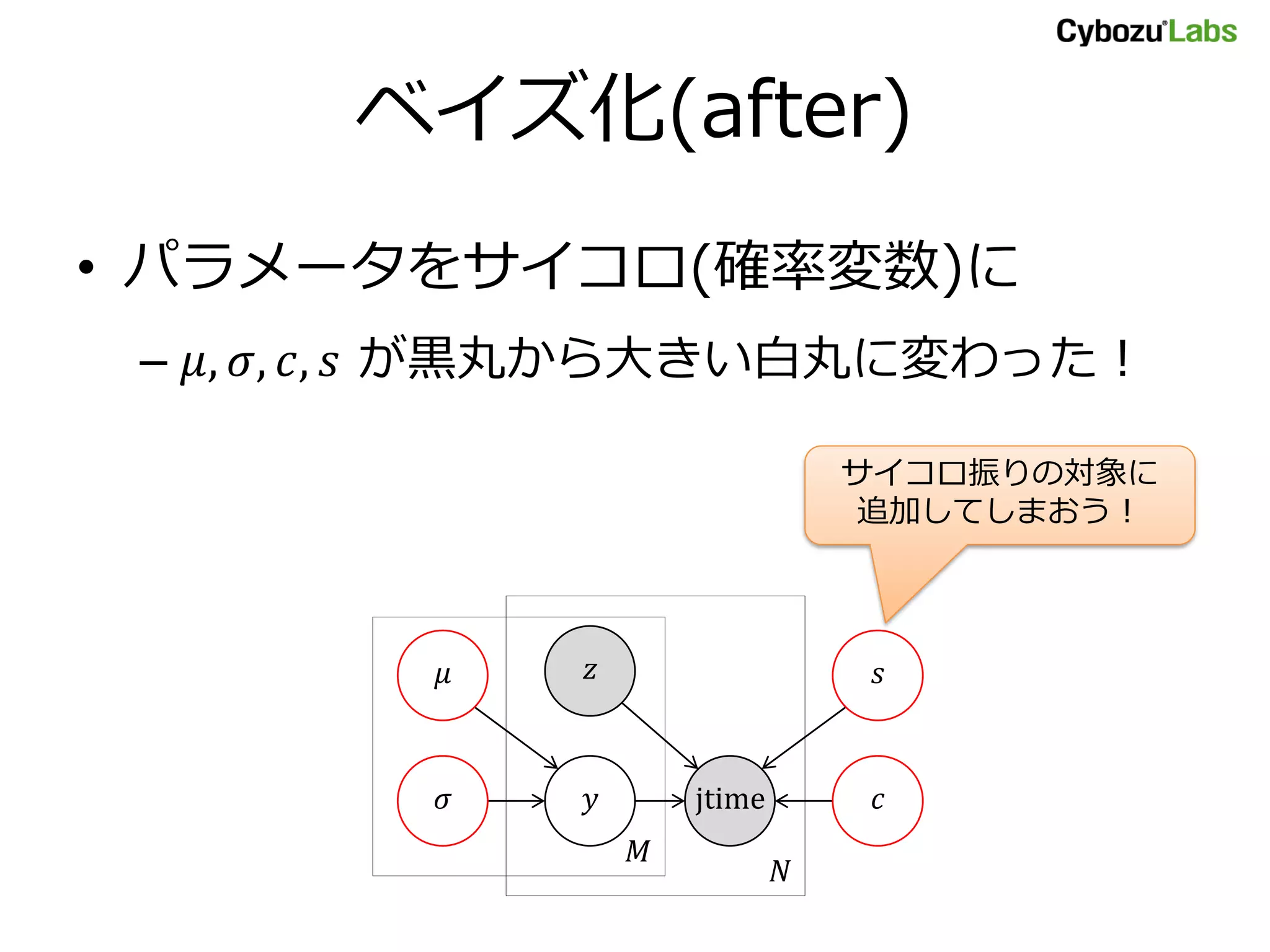
37. 事前分布
• ベイズ化による最大の相違点
– 𝜇, 𝜎, 𝑐, 𝑠 が確率変数になってしまった！
– ので、スタート地点となる分布を書いて
あげる必要があるmodel {
// 事前分布
for (m in 1:M) {
mu[m] ~ normal(0, 1);
sig[m] ~ gamma(1, 0.1);
}
c ~ normal(0, 1);
s ~ gamma(1, 1);
}
※ Stan では事前分布の指定を省略
することもできる。その場合、無情
報っぽいのが勝手に入る。今回は
データが多峰性をちょっと持つので、
正則化を効かせる感じで狭い事前分
布を明示的に入れている。

38. 推論(サイコロ振り)の実行
• rstan から Stan を呼び出し
– 10000件食わせると一昼夜かかった上、結果
を読み込むところでメモリ不足で落ちた
– 1000件で1～2時間
N <- 1000
vlg <- village[sample(nrow(village), N),] # 1000 件サンプル
library(rstan)
data <- list(N=N, M=5, jtime=vlg$jtime, z=vlg[6:10])
fit <- stan(file=stan_file, data=data)

39. サイコロ振りの様子(traceplot)
• モデルに大きな問題がないか、ざっくり確認
– 4系列がオーバーラップしてれば大丈夫(っぽいと考える)
traceplot(fit, pars=c("mu","c"))
4人で並んで
サイコロを振ってる
イメージ

40. 製品別セットアップ時間 𝑦 の分布
y <- melt(extract(fit, "y")$y, value.name="jtime")
y$lbl <- lbl[y$Var3]
ggplot(y, aes(jtime, ..density..)) +
geom_histogram(alpha=0.5, binwidth=1) +
geom_line(data=d,aes(x, y)) +
facet_wrap(~lbl) + xlim(0, 50)

41. office と skylab の 𝑦 の分布
平均 9.2秒 平均 4.8秒
• skylab のセットアップ時間はちゃんと短かった！

42. (参考)他のパラメータの推定値
> print(fit, pars=c("mu","sig","c","s"))
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
mu[1] 0.91 0.01 0.07 0.74 0.86 0.91 0.96 1.04 50 1.07
mu[2] 3.43 0.00 0.03 3.37 3.41 3.42 3.45 3.49 128 1.02
mu[3] 2.15 0.00 0.03 2.10 2.13 2.15 2.16 2.20 146 1.02
mu[4] 2.29 0.00 0.04 2.21 2.26 2.29 2.31 2.36 76 1.07
mu[5] 1.04 0.03 0.20 0.64 0.92 1.04 1.18 1.42 41 1.07
sig[1] 0.99 0.01 0.06 0.88 0.95 0.98 1.03 1.10 55 1.04
sig[2] 0.27 0.00 0.02 0.24 0.26 0.27 0.29 0.32 78 1.04
sig[3] 0.39 0.00 0.02 0.36 0.38 0.39 0.40 0.43 191 1.01
sig[4] 0.38 0.01 0.03 0.32 0.35 0.37 0.39 0.45 27 1.17
sig[5] 1.00 0.04 0.16 0.77 0.89 0.98 1.07 1.40 14 1.34
c 1.65 0.02 0.10 1.46 1.59 1.64 1.71 1.92 33 1.12
s 0.19 0.04 0.10 0.06 0.11 0.16 0.28 0.40 6 2.39
> y %>% group_by(lbl) %>% summarise(mean(jtime))
lbl mean(jtime)
(chr) (dbl)
1 garoon 31.940648
2 kintone 3.978208
3 mailwise 10.573244
4 office 9.246358
5 skylab 4.803925
★重回帰の結果
Estimate Std. Error t value Pr(>|t
(Intercept) 4.2244 0.1172 36.04 <2e-
kintone 1.5214 0.1245 12.22 <2e-
garoon 31.1726 0.1518 205.32 <2e-
office 6.7723 0.1223 55.37 <2e-
mailwise 8.4679 0.1480 57.20 <2e-
skylab 5.3662 0.1781 30.13 <2e-

43. まとめ
• 真の正解は「サービスごとのセットアップ時間をログ
に吐く」
– でもデータを取るのが高コスト or 不可能だったり
– 十分なデータを集め直すのに時間がかかったり
– という場合に、未観測変数をモデルに入れて解く方法があ
る、と知っておくと嬉しいかも
• モデルはできるだけ単純な方がいい
– でも「単純＝強い仮定」
– 仮定があわないなら、モデルを見直そう
• 本内容はブログ記事版もあります
– http://blog.cybozu.io/entry/2015/10/21/110218