1. 決定木
東京大学 三好雄也
1

2. 決定木
 決定木とは、データの特徴量を用いた簡単なルールで分岐を
作り、特徴空間を分割することを通じて判別や回帰を行うモ
デルのこと
 モデルの種類：CARTやC4.5(C5.0)
 CART
1. 木の構築：何らかの基準を満たすまで、予め定義しておいたコストに基
づいて特徴空間を2分割する手続きを繰り返す
2. 剪定(pruning)：構築された木の深さが深いほど複雑なデータを扱うこ
とができるが、過学習の可能性がある。そこで、過学習を防ぐため、予
め定めておいたパラメータによってモデルの複雑度を制御すること
 利点：高次元の判別が容易に視覚的に確認できる
2

3. 決定木のイメージ
ルートノード
線形回帰
ターミナルノード
3

4. 分類の考え方
分類の考え方
 例えば、ある商品を購入するか否かを最も良く説明する分類を作成す
るとする。この時、分類されたデータが買う、買わないできれいに分け
られれば、それは「純粋である」とされる。
 分類により、純化していく作業が決定木
4

5. 決定木の手法
 CART(Classification And Regression Trees)
 不純度を表すGINI係数を基準に分割
 ノードを分岐させることによって、不純度が減少する（＝分岐
後のそれぞれのノードの純度が増す）ような分岐点を探す
 「純度が増す」＝「バラツキが少なくなる」
 C4.5(C5.0)
 エントロピーに基づくゲイン比という基準で分割
5

6. 木の構築コスト
 木の構造T、m番目のターミナルノード𝑅 𝑚 、 𝑅 𝑚 中の例題数
𝑛𝑚
 𝑅 𝑚 において、ラベルがgになる確率
1
𝑝 𝑚,𝑔 = 𝐼[𝑦 𝑖 = 𝑔]
𝑛 𝑚
 𝑅 𝑚 におけるラベルの予測
𝑦(m) = argmax 𝑔 𝑝 𝑚,𝑔
 Tにおけるノードmのコスト𝑄 𝑚 (𝑇)
1. ジニ係数 𝑄 𝑚 𝑇 = 𝑝 𝑚,𝑔 𝑝 𝑚,𝑔′ = 𝑝 𝑚,𝑔 (1 − 𝑝 𝑚,𝑔 )
𝐺
2. エントロピー 𝑄 𝑚 𝑇 = 𝑔=1 𝑝 𝑚,𝑔 𝑙𝑜𝑔𝑝 𝑚,𝑔
6

7. ジニ係数とエントロピー
 ジニ係数で分類
 不平等さを示す指標 0~1の間の値を取り、0で平等
 ジニ係数が最も低下するように分類する。
 エントロピーに基づくゲイン（情報利得）比
 情報量を測る指標（物理では熱や物質の拡散度を示す指標）
 情報量：確率pで起こる事象の情報量は －𝑙𝑜𝑔2 𝑝 で定義される
 𝑙𝑜𝑔2 𝑝の絶対値が大きい＝情報量が多い
 エントロピー（ － 𝐺 𝑝 𝑚,𝑔 𝑙𝑜𝑔𝑝 𝑚,𝑔 ）が低いほどノードの純度は高い
𝑔=1
7

8. ジニ係数とエントロピー：教科書の例
全体で200個の例題が存在、それぞれクラスが2つ
分割1 𝑅1 にクラス1が75個、クラス2が25個
𝑅2 にクラス1が75個、クラス2が25個
分割2 𝑅1 にクラス1が50個、クラス2が100個
𝑅2 にクラス1が50個、クラス2が0個
100 75 75
ジニ係数 分割1 (1− ) ×2 = 0.1875
200 100 100
150 50 50 50 50 50
分割2 (1− ) + (1− ) = 0.1666
200 150 150 200 50 50
100 75 75
エントロピー 分割1 ×log( ) ×2 = －1.5
200 100 100
150 50 50 50 50 50
分割2 ×log( ) + ×log( ) = －0.3962
200 150 100 200 50 50
注意：C4.5などはエントロピーに基づくゲイン（情報利得）比を用いる
8

9. 決定木 in R
library(rpart) ; library(mlbench)
data(Glass)
nrow(Glass) # → 214
head(Glass) # 9つのデータと7つのType
table(Glass$Type) # 各Typeの個数
set.seed(1) # 乱数の種を指定
# 学習データ
tra.index <- sample(nrow(Glass), nrow(Glass)*0.7) # ランダムサンプリング
# ジニ係数で学習 split= “information” でエントロピー
res <- rpart(Type~., Glass[tra.index,], method=“class”, parms=list(split=“gini”))
pred <- predict(res,Glass,type=“class”) # ラベルの予測
mean(pred[tra.index]!=Glass$Type[tra.index]) # 訓練誤差 判別器を構成する際の学習データの誤り率
mean(pred[-tra.index]!=Glass$Type[-tra.index]) # 予測誤差 未知のデータに対する誤り率
# 決定木の表示
plot(res);text(res)
9

10. 木の剪定(pruning)
 木T’を構築した時、T⊂T’をT’を剪定することで得られる部分
木(subtree)とする
𝑀
 部分木Tのコスト 𝐶α (T) = 𝑚=1 𝑛 𝑚 𝑄 𝑚 (𝑇) + α 𝑇
𝑇 ：ターミナルノードの個数
α：剪定を制御するパラメータ
 学習データの適応度とαの大きさはトレードオフ
 𝐶0 (T)への寄与が小さなノードから順に剪定を行う
→ 𝐶α (T)を最小にする部分木𝑇α を探索する
 Rではαではなくオプションcpを用いる
𝐶 𝑐𝑝 (T) = 𝐶0 (T) + cp 𝑇 𝐶0 (𝑇0 ), 0≦ c ≦ 1
10

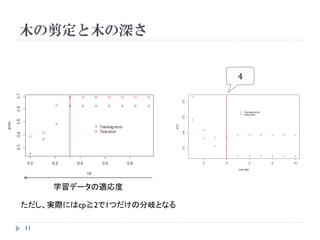
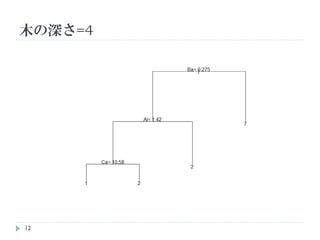
11. 木の剪定と木の深さ
4
学習データの適応度
ただし、実際にはcp≧2で1つだけの分岐となる
11

12. 木の深さ=4
12

13. 損失行列と事前確率
 クラスごとのサンプル数によって誤判別の重さが異なる
>table(Glass$Type) Glassのデータは左のようになっている。
1 2 3 5 6 7 ゆえに、サンプル数が少ないクラスである3,5,6
70 76 17 13 9 29 を誤判別するコストは小さい。
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0 1 100 100 100 1
[2,] 1 0 100 100 100 1
そこで、左図のような損失関数を導入し、3,5,6
[3,] 1 1 0 100 100 1
[4,] 1 1 100 0 100 1 の誤判別のコストを100倍にしてみる
[5,] 1 1 100 100 0 1
[6,] 1 1 100 100 100 0
0.1666667 0.1666667 …
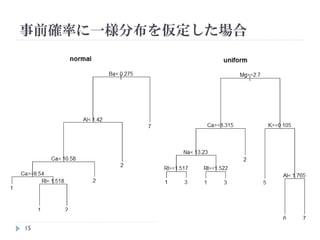
またパターン認識の本では一様分布を仮定した
分析も合わせて行っている
13

14. 損失行列と事前確率 in R
library(rpart) ; library(mlbench)
data(Glass)
set.seed(1)
tra.index <- sample(nrow(Glass),nrow(Glass)*0.7)
# 損失行列
LOSS <- matrix(1,length(levels(Glass$Type)), length(levels(Glass$Type)))
LOSS[,c(3:5)] <- 100 ; diag(LOSS)<-0
# 学習
res2 <- rpart(Type~., Glass[tra.index,], method="class", parms=list(loss=LOSS))
yhat2 <- predict(res2,Glass,type=“class”) # ラベルの予測
mean(yhat2[tra.index]!=Glass$Type[tra.index]) # 訓練誤差
mean(yhat2[-tra.index]!=Glass$Type[-tra.index]) # 予測誤差
table(true=Glass$Type, prediction=yhat2) # 判別結果
# 一様分布の場合→parms=list(prior=rep(1/6,6)
14

15. 事前確率に一様分布を仮定した場合
15

16. 決定木の不安定性
 決定木の問題点
 判別結果の分散が大きく、データが少し変わっただけで構築される
木の構造や判別ルールが大きく変わってしまう。
 14章で扱うバギング等で木の安定性を測っている。
16