1. Rで学ぶデータサイエンス
5パターン認識
第5章 混合分布モデル
2011/07/02
TwitterID:sleipnir002

2. R一人勉強会のご紹介
Rで学ぶデータサイエンス 5パターン認識
(著)金森 敬文, 竹之内 高志, 村田 昇, 金 明哲
共立出版
今ならデモスクリプトがダウンロードできる!
http://www.kyoritsu-
pub.co.jp/service/service.html#019256
彼女いない暦の５年８ヶ月の不細工でモテな私が
第1章 判別能力の評価 Done
第2章 k-平均法
第3章 階層的クラスタリング
あのかわいい女の子を
たったの３ヶ月でGET！！
第4章 混合正規分布モデル
第5章 判別分析
第6章 ロジスティック回帰
第7章 密度推定 はっと息を飲むようなあの美人がこの方法で
第8章 k-近傍法 Rでパターン認識ができるように、
第9章 学習ベクトル量子化
第10章 決定木 その結果、驚愕の真実が！
第11章 サポートベクターマシン
第12章 正則化とパス追跡アルゴリズム
第13章 ミニマックス確率マシン
第14章 集団学習 さぁ、今すぐAmazonでクリック！！
第15章 2値判別から多値判別へ

3. 前回のあらすじ
• 前回は第2 回としてK-means分析を学んだよ！
• K-Meansのクラスタ数Kを推定する方法
– カーネル主成分分析による可視化
– ギャップ統計量による推定
L'k
元のデータ カーネル主成分
Gk  log  log L'k  log Lk
Lk
ギ
ャ
ッ
プ
統
計
量
クラスタ数K

4. 第5章の目的
混合分布による教師なしクラスタリング
EMアルゴリズムによるモデル推定
• キーワード
– 混合分布
– EMアルゴリズム
– AIC、BIC

5. 混合正規分布によるクラスタリングを理解する

6. 混合正規分布とは（１）
• 混合正規分布とは複数の正規分布を混ぜあ
わせた物
M
p( x; )   m ( x; m , m )
m 1

7. 混合正規分布とは（２）
M
p( x; )   m ( x; m , m )
m 1
• ちなみにπも確率  m ;   m  1,  m  0, m  {1,..., M }
m
  {1 m } パイは異なる
• θはパラメータ 正規分布を
重み付ける
m  { m , m , m }

8. 混合分正規分布から
教師なしクラスタリングへ
1. ２つの要素正規分布から、混合正規分布が構成さ
れデータが発生する。
2. 混合正規分布モデルの下で、あるデータがもっとも
発生した要素がデータの属するクラスタである。
逆にデータか 要素からデー
ら要素を推定 タが生成され
する。 たと考える。

9. 混合正規分布による
教師なしクラスタリング
• ベイズの定理を使うと…
p( x, m; )
p(m | x; ) 
p ( x; )
ただのベイズの定理
 m ( x;  m ,  m )
 M

m 1
 ( x;  m ,  m )
m
⇒モデルがわかれば、教師なしクラスタリングがで
きる。

10. クラスタリングを行うために
• モデルが与えられれば（パラメータが与えら
れれば）、クラスタリングができる
• 次に考えるのはデータからモデルを推定する
こと。
既にあるデータ モデルθ クラスタリング
 x11  x1 p  arg m max p(m | x)
 
X     
x  x  m
 n1 np 
新データ
 x1 
 
x  
x 
 n

11. データからモデルを推定する
• データが与えられたときのパラメータθの推定
をどうするか？
– 最尤推定は？
n
  arg Max  log p( xi ; )
ˆ

i 1
n
 arg Max  log   m ( xi ; )

i 1
⇒logの中に∑があるので、陽に解析できない。

12. じゃあ、どうやって推定する？
• しかし、最尤推定を行いたい。
• →パラメータｘとモデルを表すラベルmの対、( xi , mi )
が明らかになっていれば計算できる
（証明は教科書で）
n
  arg Max  log p( xi , mi ; )
ˆ
n
  arg Max  log p( xi ; )
ˆ

 i 1
i 1
ラベルを与える
n
 arg Max  log  m ( xi , mi ; )
n
 arg Max  log   m ( xi ; ) 
 i 1
i 1
⇒どのように、 xi , mi )を与えるか？
(

13. EMアルゴリズム
• EMアルゴリズム・・・反復によって欠損データの最尤推定を
行う方法
• 混合分布の場合、所与のデータが属するラベルが欠損して
いると考える。
通常のデータ行列 EMアルゴリズムで扱うデータ行列
欠けたデータ
 x11  x1 p   x11  x1 p m1 
   
X      X      
x  x  x  x m 
 n1 np   n1 np n

14. EMアルゴリズムの計算手順
Eステップ：あるθtを用いて、Q関数を計算する。
• モデルの事後確率に基づく対数尤度→最大化する
n M
Q( , )   p(m | xi ; (t ) ) log p( xi , m; )
(t )
i 1 m 1
Mステップ：Q関数を最大化するθtを求める
• ステップtにおけるθの最大化
 (t )  arg Max Q( , (t ) )

15. EMアルゴリズムのイメージ
• 言葉で言ってもわからないので、可視化した
ものをみてみましょう。
入力： Eステップ：
データX Q( , (t ) )
 x11  x1 p  の計算
  出力：
    
x  x  t=t++ パラメータ:θ
 n1 np 
Mステップ：
パラメータ初期値θ’ Q( )
の最大化
＊アルゴリズムの詳細は下記リンクをチェック！
http://vrl.sys.wakayama-u.ac.jp/PRA/EM/MixtureEMj.html

16. EMアルゴリズムの正当性
• この繰り返しの中、Q関数つまり尤度関数は
単調増加になる。
– 証明は教科書を参照

17. RでEMアルゴリズムによってクラスタリング
Mclustパッケージ

18. Mclustによるクラスタリングの
大まかな流れ
パッケージ：MClust
結果の可視化：
モデル推定：Mclust
mclust2Dplot
引数１：データX 引数2：データX
所与のデータX 複数のモデルの中からBICの高い 引数2：Mclustのprameters
ものを選択してMclustオブジェク 引数3：可視化内容
トを返す 結果を可視化する
事後確率の計算:
分類：map
cdens
引数１：予測したい新データX’ 引数１：cdensの事後確率
予測したいデータx’ 引数２：Mclustのparameters もっとも事後確率の高いラベ
データの事後確率を計算する。 ルのデータを返す。
注：関数のデータの大まかなながれです。引数は他に色々あるので注意してください。

19. データセット
• 用いるデータセットはmlbench.smily
４クラス
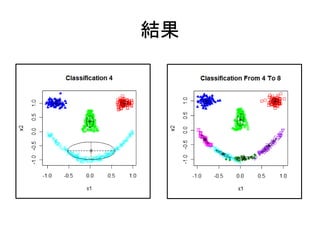
データ

20. 混合分布でクラスタリングする
library(mclust); library(mlbench) Package mclust
dat <- mlbench.smiley()
colnames(dat$x) <- c("x1","x2")
dev.new()
(gmm4 <- Mclust(dat$x,G=4))
混合正規分布モデルの
mclust2Dplot(dat$x,parameters=gmm4$parame 推定、要素数G=4
ters,z=gmm4$z,what="classification")
title("Classification 4") 判別結果をプロット
dev.new()
(gmmup8 <- Mclust(dat$x,G=4:8)) 要素モデルの数を4とす
mclust2Dplot(dat$x,parameters=gmmup8$para る
meters,z=gmmup8$z,what="classification")
title("Classification From 4 To 8") 要素モデルの数を4から
8とする

21. 結果

22. 予測を行うmapとcdens
• Cdens関数でテストデータの事後確率を計算
• Map関数でラベルに変換
#40のテストデータ、gmmup8をモデルで実験
testdat <- mlbench.smiley(n=40)
colnames(testdat$x) <- c("x1","x2")
dev.new()
testc1<-map(cdens(modelName=
gmmup8$modelName, data=testdat$x,
parameters=gmmup8$parameters))
mclust2Dplot(testdat$x,
parameters=gmmup8$parameters,
classification=testc1)

23. ModelNamesオプション
• Mclustパッケージではモデルとして以下のオ
プションの中から希望のものを指定できる。
#e.g.
(gmm5 <- Mclust(dat$x,G=5, modelNames="EEE"))
mclust2Dplot(dat$x,parameters=gmm5$parameters,z=gmm5$z,what="classification")
title("EEE")
注：全部で10種類指定できる。指定しないと、一番当てはまりのよいものを使用する。

24. おまけ

25. ここで疑問

26. モデルの数をいくつにすればよいのか？

27. 混合数の推定
• 混合数の推定＝モデルの妥当性の検証
– 交差検証法
• 第１回で説明済み
→you! Forループまわしてプログラム書いちゃいなよ。
– 情報量を用いる
• AIC：赤池情報量基準
– 特定のパラメータのあてはまりのよさ
• BIC：ベイズ情報量基準
– モデル全体でのあてはまりのよさ
– Mclustではモデルの選択にBICを用いている。

28. BIC
• 複数のモデルが等しい事前確率で選択され
ると仮定した上で、尤度の期待値

BIC  2nE log  p( X ; ) p(l | D)dl 
n
BIC ( l )  2 log p( xi ; ) |  l | log n
ˆ ˆ ˆ
i 1
モデルVVVの要素数７
がBICがもっとも高いの
でMclustで選ばれる。
gmm<-Mclust(dat$x)
plot.mclustBIC(gmm$BIC, legendArgs=list(x="bottomright", cex=0.7, ncol=2))