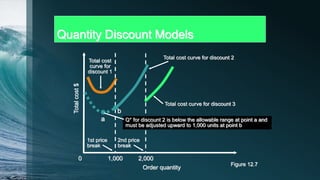
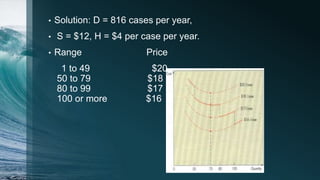
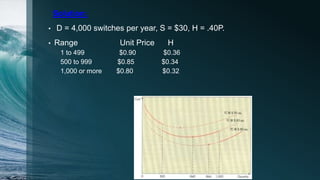
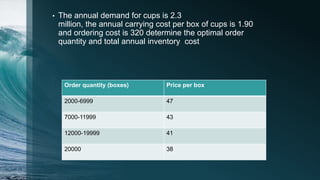
1. The document discusses quantity discount models, including calculating optimal order quantities (Q*) based on setup, holding, and product costs to determine the lowest total cost. 2. It provides examples of applying these models to determine optimal order quantities for various products given annual demand, costs, and discount price structures. 3. The optimal order quantity is the one that results in the lowest total annual cost based on comparing total costs calculated for different possible order sizes.

1. QUANTITY
DISCOUNT
MODLE

2. Quantity Discount Models
 Reduced prices are often available when
larger quantities are purchased
 Trade-off is between reduced product cost and
increased holding cost
Total cost = Setup cost + Holding cost + Product
cost
TC = S + H + PD
D
Q
Q
2

3. Quantity Discount Models
1. For each discount, calculate Q*
2. If Q* for a discount doesn’t qualify, choose
the smallest possible order size to get the
discount
3. Compute the total cost for each Q* or
adjusted value from Step 2
4. Select the Q* that gives the lowest total
cost
Steps in analyzing a quantity discount

4. Quantity Discount Models
1,000 2,000
Totalcost$
0
Order quantity
Q* for discount 2 is below the allowable range at point a and
must be adjusted upward to 1,000 units at point b
a
b
1st price
break
2nd price
break
Total cost
curve for
discount 1
Total cost curve for discount 2
Total cost curve for discount 3
Figure 12.7

5. Example:1
• The maintenance department of a large hospital
uses about 816 cases of liquid cleanser annually.
Ordering costs are $12, carrying costs are $4 per
case per year, and the new price schedule indicates
that orders of less than 50 cases will cost $20 per
case, 50 to 79 cases will cost $18 per case, 80 to 99
cases will cost $17 per case, and larger orders will
cost $16 per case. Determine the optimal order
quantity and the total cost.

6. • Solution: D = 816 cases per year,
• S = $12, H = $4 per case per year.
• Range Price
1 to 49 $20
50 to 79 $18
80 to 99 $17
100 or more $16

7. • Compute the common
EOQ: √2DS/H = √ 2(816)*12/4 = 70 cases.
• The 70 cases can be bought at $18 per case because 70 falls in the range
of 50 to 79 cases. The total cost to purchase 816 cases a year, at the rate
of 70 cases per order, will be
Total cost =(Q/2)H+(D/Q)S+PD
TC =(70/2)*4+(816/70)*12+18*816 = $ 14.98
• Because lower cost ranges exist, each must be checked against the
minimum cost generated by 70 cases at $18 each. In order to buy at $17
per case, at least 80 cases must be purchased. (Because the TC curve is
rising, 80 cases will have the lowest TC for that curve's feasible region.)
The total cost at 80 cases will be
TC =(80/2)*4+(816/80)*12+17*816 = $ 14.154
• To obtain a cost of $16 per case, at least 100 cases per order are required,
and the total cost will be
TC =(100/2)*4+(816/100)*12+16*816 = $ 13.354
• Therefore, because 100 cases per order yields the lowest total cost, 100
cases is the overall optimal order quantity.

8. Example:2
• Surge Electric uses 4,000 toggle switches a year.
Switches are priced as follows: 1 to 499, 90 cents
each; 500 to 999, 85 cents each; and 1,000 or more,
80 cents each It costs approximately $30 to prepare
an order and receive it, and carrying costs are 40
percent of purchase price per unit on an annual basis.
Determine the optimal order quantity and the total
annual cost.

9. Solution:
• D = 4,000 switches per year, S = $30, H = .40P.
• Range Unit Price H
1 to 499 $0.90 $0.36
500 to 999 $0.85 $0.34
1,000 or more $0.80 $0.32

10. • Find the minimum point for each price, starting with the lowest
price, until you locate a feasible minimum point.
Minimum point at (.80) = √ 2DS/H
= √ 2(4000)*30/0.32
= 866 Switches.
• Because an order size of 866 switches will cost $0.85 each
rather than $0.80 each, 866 is not a feasible minimum point for
$0.80 per switch. Next, try $0.85 per unit.
Minimum point at (.85) = √ 2DS/H
= √ 2(4000)*30/0.34
= 840 Switches.
• This is feasible; it falls in the $0.85 per switch range of 500 to
999.

11. • Now compute the total cost for 840, and compare it to the
total cost of the minimum quantity necessary to obtain a price
of $0.80 per switch.
• Total cost for(840) = (Q/2)H+(D/Q)S+PD
TC = (840/2)*.34+(4000/840)*30+0.85*4000
= $ 3,686
Total cost for(1000) = (Q/2)H+(D/Q)S+PD
TC = (1000/2)*.32+(4000/1000)*30+0.80*4000
= $ 3,480
• Thus, the minimum-cost order size is 1,000 switches.

12. Salman, a distributor of audio and video equipment wants to reduce
a large stock of television .It has offered a local chain of stores a
quantity discount pricing schedule as given above.
The annual carrying cost for the stores for a TV is $190, the
ordering cost is $ 2500 and annual demand for a particular model
TV is estimated to be 200 units . The chain wants to determine if it
should take advantage of this discount or order the basic EOQ order
size.
QUANTITY PRICE
1-49 $1400
50-89 1100
90+ 900
EXAMPLE :3

13. Solution
First determine the optimal order size and total cost
with the basic EOQ model.
S = $ 2500
H = $ 190 per TV
D = $ 200 TVs per year
Q opt = √2CoD / Cc
=√2(2500)(200) / 190
= 72.5 TVs
Although we will use Qopt = 72.5 in the subsequent
computations , realistically the order size would be 73
televisions. This order size is eligible for the first

14. Continuation
Tc min = H( Q opt / 2) + S (D / Q opt )+ PD
= (190)(72.5/ 2 ) + (2500)(200 / 72.5 ) +
(1100)(200)
TC min = $ 233, 784
Since there is discount for a larger order size than 50 units
(i.e.., there is a lower cost curve ),this total cost of $233,784
must be compared with total cost with an order size of 90
and a discounted price of $ 900.

15. Continuation
TC = H(Q opt / 2) + S(D / Q opt ) + PD
= (190)(90 / 2 ) + (2500)(200/ 90 ) + (900)(200)
= $ 194,105
Since this total cost is lower($ 194,105 < $ 233,784) , the
maximum discount price should be taken , and 90 units should be
ordered . We know that there is no order size larger than 90 that
would result in a lower cost , since the minimum point on this
total cost curve has already been determined to be 73.

16. EXAMPLE:3
• A Supplier of the 10000 value has offered Mr. Swartz
quantity discounts if he will purchase more than his order
quantities. The new volumes and prices are:
• range of order Acquisition of
cost per value(ac)
1- 399 $ 2.20
400-699 $ 2.00
700+ $ 1.80

17. • D=10000 values per year ,H= $ 0.20(ac) per value,
• S= $ 5.50 per year
• The EOQs are competed for each of the acquisition costs:
EOQ (2.20)= √2DS/H
= √2(10000)(5.5)/(0.2*2.2) =500
EOQ (2.00)= √2DS/H
= √2(10000)(5.5)/(0.2*2.0) =524.4
EOQ (1.80)= √2DS/H
= √2(10000)(5.5)/(0.2*1.80) = 552.8

18. • Mary Ann notes that only EOQ(2.00) is feasible because
524.4 valves per order can be purchased at $ 2.00 per
value .The TMC at two quantities is investigated 524.4
units per order and 700 units per order
• Q=524.4 TMC=(Q/2)H+(D/Q)S+PD
=(524.4/2)(0.2*2.0)+(10000/524.4)5.5+
(10000*2)
= 104.88+104.88+20000 $ 20,209.76 per year
• Q=700 TMC=(Q/2)H+(D/Q)S+PD
=(700/2)(0.2*1.8)+(10000/700)5.5+
(10000*1.8)
=126.00+78.57+18000 $ 18,204.57 per year

19. EXAMPLE : 4
• The 21000 seat Air east Arena houses the local
professional ice hockey, basketball, indoor soccer and
arena football teams as well as various trade shows
wrestling and boxing matches, tractor pulls and circuses.
Arena vending annually sells large quantities of soft drinks
and been in plastic cups with the name of the arena. The
local container cup manufacturer that supplies the cups in
boxes of 100 has offered arena management the following
discount price schedule for cups

20. • The annual demand for cups is 2.3
million, the annual carrying cost per box of cups is 1.90
and ordering cost is 320 determine the optimal order
quantity and total annual inventory cost
Order quantity (boxes) Price per box
2000-6999 47
7000-11999 43
12000-19999 41
20000 38

21. EOQ= 2𝐾𝐷/ℎ
= 2 ∗ 2300 ∗ 320/1.9
=2783
TCU=
320∗2300
2783
+
2783∗1.9
2
+ (23000*47)
=1086289
TCU=
320∗23000
11999
+
11999∗1.9
2
+ (2300*43)
=1001012
SOLUTION
D = 2.3 *1000000/100
= 230000
k = 320
h = 1.9

22. • TCU=
320∗23000
19999
+
19999∗1.9
2
+ (23000*41)
=962367
TCU=
320∗23000
20000
+
20000∗1.9
2
+ (23000*38)
=893368
∴Total cost is 893368 and EOQ is 20000.