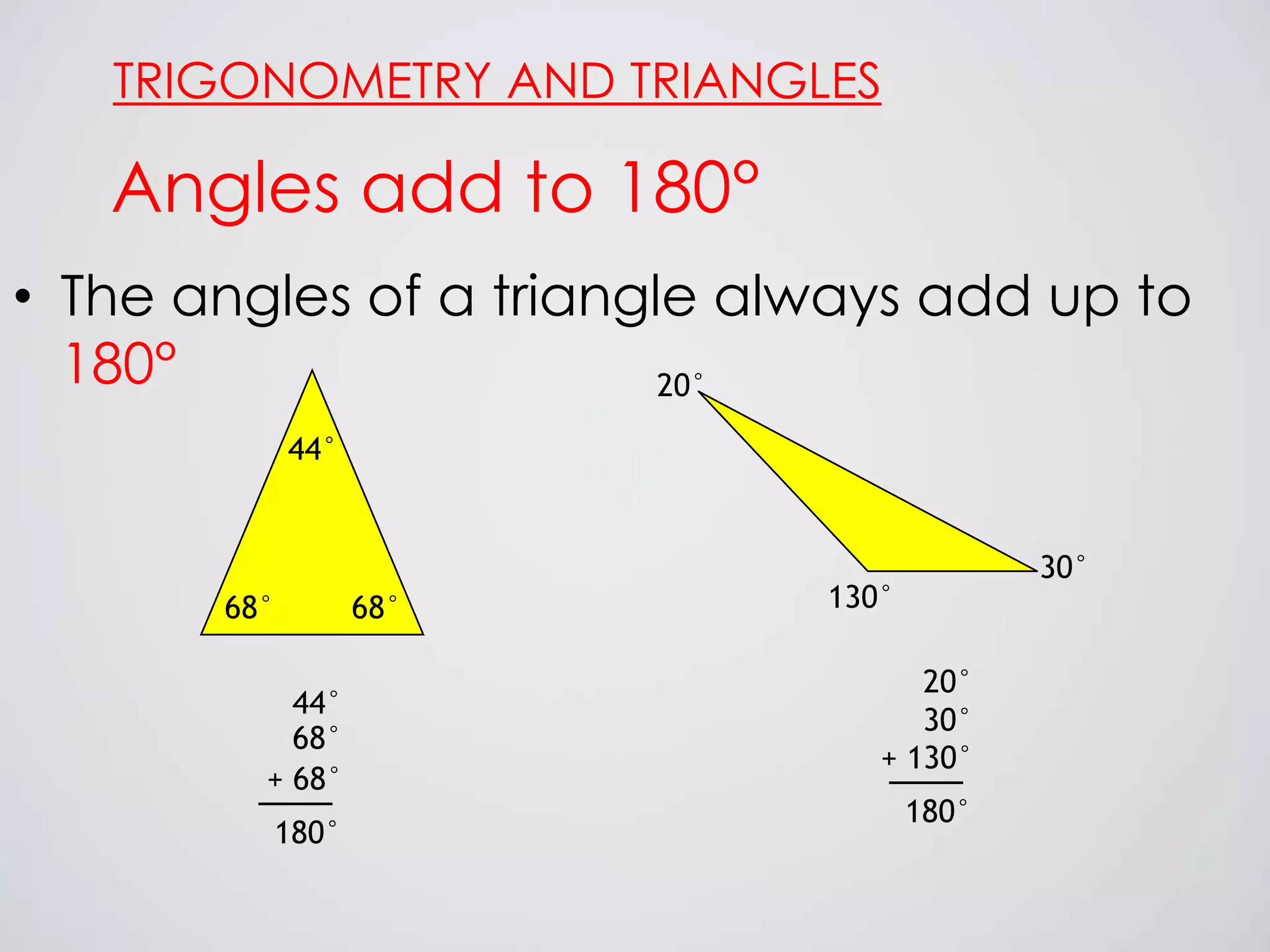
Trigonometry studies the relationships between the sides and angles of triangles. It has been studied since ancient times in Egypt and Babylon. Modern trigonometry uses trigonometric functions like sine, cosine, and tangent to define ratios of the sides of a right triangle based on a particular angle. These functions allow calculation of unknown side lengths or angles when some information is known. Fields like navigation, surveying, and engineering extensively use trigonometric functions and formulas like the Pythagorean theorem.

1. TRIGONOMETRY

2. INTRODUCTION
Trigonometry is a branch
of mathematics that
studies triangles and the
relationships between the
lengths of their sides and
the angles between those sides.

3. HISTORY OF TRIGONOMETRY
Early study of triangles can be traced to
the 2nd millennium BC, in Egyptian
mathematics and Babylonian
mathematics. Systematic study of
trigonometric functions began
in Hellenistic mathematics, reaching
India as part of Hellenistic astronomy.

4. Uses of trigonometry
Scientific fields that make use of trigonometry
include:
architecture, astronomy, civil
engineering, geophysics, electrical
engineering, electronics, land surveying
and many physical sciences, mechanical
engineering, oceanography, optics, pharmac
ology, probability theory, seismology, statistics.

5. TRIGONOMETRY AND
TRIANGLES
Using Trigonometry we can find
the relationships between the
lengths of sides of the triangle
and the angles between those
sides.

6. TRIGONOMETRY AND TRIANGLES
Angles add to 180°
• The angles of a triangle always add up to
180°
20°
44°
68°
44°
68°
+ 68°
180°
68°
30°
130°
20°
30°
+ 130°
180°

7. TRIGONOMETRY AND TRIANGLES
Right triangles
• We only care about right triangles.
– A right triangle is one in which one of the angles is 90°
– Here’s a right triangle:
opposite
Here’s the
right angle
Here’s the angle
we are looking at
adjacent
• We call the longest side the hypotenuse
• We pick one of the other angles--not the right angle
• We name the other two sides relative to that angle

8. TRIGONOMETRY AND TRIANGLES
The Pythagorean Theorem
If you square the length of
the two shorter sides and
add them, you get the
square of the length of the
hypotenuse
adj2 + opp2 = hyp2
32 + 42 = 52, or 9 + 16 = 25

9. TRIGONOMETRY AND TRIANGLES
The Pythagorean Theorem
• There are few triangles with
integer sides that satisfy the
Pythagorean formula
• 3-4-5 and its
multiples (6-8-10, etc.)
are the best known
• 5-12-13 and its multiples
form another set.
• 25 + 144 = 169
opp
adj

10. TRIGONOMETRY AND TRIANGLES
Ratios
opposite
• Since a triangle has three
sides, there are six ways to
divide the lengths of the
sides
adjacent
• Each of these six ratios has a
name (and an abbreviation)
• Three ratios are most used:
• The ratios depend on
– sine = sin = opp / hyp
the shape of the triangle
– cosine = cos = adj / hyp
(the angles) but not on
– tangent = tan = opp / adj
the size
• The other three ratios are
redundant with these and
can be ignored

11. TRIGONOMETRY AND TRIANGLES
Using the ratios
opposite
• With these functions, if you know an angle (in addition
to the right angle) and the length of a side, you can
compute all other angles and lengths of sides
adjacent
• If you know the angle marked in blue (call it A) and
you know the length of the adjacent side, then
– tan A = opp / adj, so length of opposite side is given by
opp = adj * tan A
– cos A = adj / hyp, so length of hypotenuse is given by
hyp = adj / cos A

12. TRIGONOMETRY AND TRIANGLES
Important Formulas
• The formulas for right-triangle
trigonometric functions are:
– Sine = Opposite / Hypotenuse
– Cosine = Adjacent / Hypotenuse
– Tangent = Opposite / Adjacent
• Mnemonics for those formulas are:
– Some Old Horse Caught Another Horse
Taking Oats Away
– Saints On High Can Always Have Tea Or
Alcohol

13. THANK YOU
By – Remin Rajesh