Recommended
PDF
PDF
PDF
PPTX
マルコフ連鎖モンテカルロ法 (2/3はベイズ推定の話)
PDF
PDF
PDF
PPTX
PDF
PDF
PDF
PPTX
PDF
PDF
PDF
PDF
PDF
ガウス過程回帰の導出 ( GPR : Gaussian Process Regression )
PDF
PDF
PPTX
PDF
PDF
PDF
PDF
PPTX
PDF
非制約最小二乗密度比推定法 uLSIF を用いた外れ値検出
PPTX
PDF
PPTX
論文紹介 Markov chain monte carlo and variational inferences bridging the gap
PDF
【Zansa】第12回勉強会 -PRMLからベイズの世界へ
More Related Content
PDF
PDF
PDF
PPTX
マルコフ連鎖モンテカルロ法 (2/3はベイズ推定の話)
PDF
PDF
PDF
PPTX
What's hot
PDF
PDF
PDF
PPTX
PDF
PDF
PDF
PDF
PDF
ガウス過程回帰の導出 ( GPR : Gaussian Process Regression )
PDF
PDF
PPTX
PDF
PDF
PDF
PDF
PPTX
PDF
非制約最小二乗密度比推定法 uLSIF を用いた外れ値検出
PPTX
PDF
Similar to 自動微分変分ベイズ法の紹介
PPTX
論文紹介 Markov chain monte carlo and variational inferences bridging the gap
PDF
【Zansa】第12回勉強会 -PRMLからベイズの世界へ
PPTX
PPTX
PDF
PPTX
PDF
RStanとShinyStanによるベイズ統計モデリング入門
PDF
確率的深層学習における中間層の改良と高性能学習法の提案
PDF
RBM、Deep Learningと学習(全脳アーキテクチャ若手の会 第3回DL勉強会発表資料)
PDF
PPTX
第3回nips読み会・関西『variational inference foundations and modern methods』
PDF
単純ベイズ法による異常検知 #ml-professional
PDF
PDF
PDF
Jubatusにおける大規模分散オンライン機械学習
PDF
PDF
Infer net wk77_110613-1523
PDF
Stanの紹介と応用事例(age heapingの統計モデル)
PDF
PDF
More from Taku Yoshioka
PDF
PDF
PDF
PDF
PDF
PDF
PDF
20171207 domain-adaptation
PDF
PDF
自動微分変分ベイズ法の紹介 1. 2. 3. 4. 5. 6. 7. 8. 9. ADVI の制限
1. 離散確率変数を扱うことができません.
• 勾配法による最適化を⾏うためです.
• 観測変数は離散値でも OK です.
2. 近似事後分布はサンプリングが簡単に実⾏できるものに
限られます.
• Stan, PyMC3 共に正規分布を仮定します.
• Stan は多変量正規分布もサポートします.
9
10. PyMC3 のコード例
• Automatic relevance determination (ARD)
• Gaussian mixture model
• Latent Dirichlet Allocation (LDA)
10
11. コード例: Automatic relevance determination (ARD)
• with ブロックで確率モデルを記述します.
• 必要な変数変換は⾃動的に適⽤されます (ここでは alphas, beta).
• pm.variational.advi() にモデルを渡すことで ADVI が実⾏されま
す.
• 戻り値 mean はパラメータ事後分布の平均値です.
with Model() as model:
# Prior precisions
alphas = Gamma('alphas', alpha=1e-6, beta=1e-6, shape=(n_features,))
beta = Gamma('beta', alpha=0.1, beta=0.1, shape=(1,))
w = Normal('w', mu=0.0, tau=alphas, shape=(n_features,))
Normal('l', mu=xs_.dot(w), tau=beta, observed=ys)
means, _, elbos = pm.variational.advi(
model=model, n=1000, learning_rate=0.1, accurate_elbo=True)
w_post = means['w']
11
12. 13. コード例: Gaussian mixture model
• LogSumExp を⽤いて⽣成コンポーネントを表す確率変数を周辺
消去します.
• 尤度関数を記述すれば様々な混合分布をモデル化できます
(e.g., 正規分布+⼀様分布)
from pymc3.math import LogSumExp
# Log likelihood of normal distribution
def logp_normal(mu, tau, value):
# log probability of individual samples
k = tau.shape[0]
delta = lambda mu: value - mu
return (-1 / 2.) * (k * tt.log(2 * np.pi) + tt.log(1./det(tau)) +
(delta(mu).dot(tau) * delta(mu)).sum(axis=1))
# Log likelihood of Gaussian mixture distribution
def logp_gmix(mus, pi, tau):
def logp_(value):
logps = [tt.log(pi[i]) + logp_normal(mu, tau, value)
for i, mu in enumerate(mus)]
return tt.sum(LogSumExp(tt.stacklists(logps)[:, :n_samples], axis=0))
return logp_
13
14. コード例(続き)および実⾏結果
• DensityDist() を使って様々な尤度関数を定義できます.
with pm.Model() as model:
mus = [MvNormal('mu_%d' % i, mu=np.zeros(2), tau=0.1 * np.eye(2), shape=(2,)
for i in range(2)]
pi = Dirichlet('pi', a=0.1 * np.ones(2), shape=(2,))
xs = DensityDist('x', logp_gmix(mus, pi, np.eye(2)), observed=data)
• ミニバッチを使うことで⼤量データに対する推定も可能です.
100,000 サンプルに対する GMM の平均推定結果.
14
15. コード例: Latent Dirichlet Allocation (LDA)
• PyMC3 のバックエンドである Theano の機能を使って,
スパース⾏列として与えられたデータから対数尤度を計算でき
ます.
def logp_lda_f2(phi, thetas):
def ll_docs_f(tfs):
dixs, vixs = tfs.nonzero()
vfreqs = tfs[dixs, vixs]
ll_docs = vfreqs * LogSumExp(
tt.log(thetas[dixs] + 1e-10) + tt.log(phi[vixs] + 1e-10), axis=1).ra
return tt.sum(ll_docs)
return ll_docs_f
with pm.Model() as model:
thetas = pm.Dirichlet('thetas', a=1.0 * np.ones((n_topics, n_samples)), shap
phi = pm.Dirichlet('phi', a=1.0 * np.ones((n_features, n_topics)), shape=(n_
doc = pm.DensityDist('doc', logp_lda_f2(phi, thetas.T), observed=tfs.toarray
15
16. 最後に
PyMC3 の ADVI は実装されたばかりですが, より多くの⼈に使って
頂きたいと思います.
• PyMC3 のウェブサイト:
https://pymc-devs.github.io/pymc3/getting_started/
• ADVI のコード例:
• https://gist.github.com/taku-y/d68fdc893ff808468a98b400b2e059a2
• https://gist.github.com/taku-y/a884a0ee78fb89bf5735
Stan の ADVI はより洗練されたものとなっています.
• ADVI の Python インターフェースの有無は未調査です.
16
17. 変分ベイズ法 (1/2)
事後分布 p(X|D) を適当な分布 q(X) で近似して, 真の事後分布との
KL ダイバージェンス KL(q(X)||p(X|D)) に近づけます.
変分下限
周辺尤度 log p(D) = log
∫
p(D, X)dX と KL ダイバージェンスの間に
次の関係が成り⽴ちます:
log p(D) = L[q(X)] + KL(q(X)||p(X|D))
L[q(X)] ≡ Eq(X)[log p(D, X) − log q(X)]
KL(·||·) ≥ 0 より log L[q(X)] ≤ log p(D), つまり L[q(X)] は周辺尤度
の下限であり, Evidence lower bound (ELBO) と呼ばれます
([HBW+13]).
17
18. 変分ベイズ法 (2/2)
変分ベイズ法による事後分布の推定
log p(D) は q(X) に依存しないので, q(X) に関する ELBO の最⼤化は
q(X) と p(X|D) の KL ダイバージェンスの最⼩化と等価であること
が
分かります.
尤度関数 p(D|X) に対して p(X) が共役事前分布の場合,
ELBO が最⼤となる q(X) は p(X) と同じ分布族となります.
q(X1, X2) = q(X1)q(X2) と仮定し, かつそれぞれが共役事前分布の
場合, ELBO を q(X1) と q(X2) について交互に最⼤化するアルゴリズ
ムを
構成できます (EM アルゴリズムと同様のパラメータ更新則を得ま
す).
18
19. 確率的変分ベイズ法 (1/2)
q(X) に任意の分布を使うため, q(X) を θ でパラメトライズされる
分布族とし, ELBO に対して勾配法を適⽤します.
ELBO のパラメータに関する勾配 ∇θL[q(X)] を計算する⽅法として,
次の⼆つがあります ([TL15]):
1. Log-derivative trick: ∇θq(X) = q(X)∇θ log q(X) を利⽤します.
2. Reparametrization trick: パラメータを持たない分布 q(Z) と変数
変換 X = g(Z; θ) で q(X) を表現し, q(X) に関する期待値を (パ
ラメータを持たない) q(Z) に関する期待値に置き換えます.
いずれの場合も, 勾配を期待値として計算できます:
∇θL[q(X)] = Eq(X)[f(X)]
(あるいは Eq(Z)[f(Z)])
19
20. 21. 22. 参考⽂献
• [BT00] Bishop, C. M., & Tipping, M. E. (2000, June). Variational relevance
vector machines. In Proceedings of the Sixteenth conference on Uncertainty in
artificial intelligence (pp. 46-53). Morgan Kaufmann Publishers Inc.. ARD の変
⽂ベイズ版.
• [TL14] Titsias, M., & Lázaro-Gredilla, M. (2014). Doubly stochastic variational
Bayes for non-conjugate inference. In Proceedings of the 31st International
Conference on Machine Learning (ICML-14) (pp. 1971-1979). 期待値のサンプリ
ングとデータのサンプリングを組み合わせた⼿法.
• [HBW+13] Hoffman, M. D., Blei, D. M., Wang, C., & Paisley, J. (2013).
Stochastic variational inference. The Journal of Machine Learning Research,
14(1), 1303-1347. データのサンプリングによって変分ベイズ法を⼤規模データ
に適⽤する⼿法.
• [RM51] Robbins, H., & Monro, S. (1951). A stochastic approximation method.
The annals of mathematical statistics, 400-407. 確率近似法.
• [TL15] Titsias, M., & Lázaro-Gredilla, M. (2015). Local Expectation Gradients
for Black Box Variational Inference. In Advances in Neural Information
Processing Systems (pp. 2620-2628). MC サンプリングを求積法に置き換えた⼿
法.
• [KRG+15] Kucukelbir, A., Ranganath, R., Gelman, A., & Blei, D. (2015).
Automatic variational inference in stan. In Advances in Neural Information
Processing Systems (pp. 568-576). ADVI とその Stan 実装の解説.
22

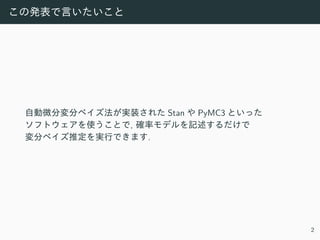




![⾃動微分変分ベイズ法
• 確率変数の変換と確率的最適化を組み合わせることで
変分ベイズ推定を⾃動的に実⾏する⽅法です ([KRG+15]).
• Automatic differentiation variational inference
(ADVI) と呼ばれます.
• MCMC と変分ベイズ法の⻑所を兼ね備えた⽅法です:
• 複雑な式の導出が不要
• 収束が速い
• Stan, PyMC3 に実装されています.
7](https://image.slidesharecdn.com/slide-160416103223/85/slide-7-320.jpg)
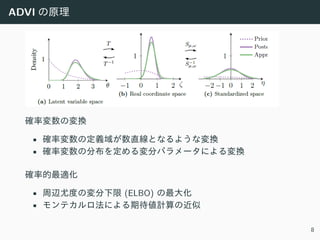


![コード例: Automatic relevance determination (ARD)
• with ブロックで確率モデルを記述します.
• 必要な変数変換は⾃動的に適⽤されます (ここでは alphas, beta).
• pm.variational.advi() にモデルを渡すことで ADVI が実⾏されま
す.
• 戻り値 mean はパラメータ事後分布の平均値です.
with Model() as model:
# Prior precisions
alphas = Gamma('alphas', alpha=1e-6, beta=1e-6, shape=(n_features,))
beta = Gamma('beta', alpha=0.1, beta=0.1, shape=(1,))
w = Normal('w', mu=0.0, tau=alphas, shape=(n_features,))
Normal('l', mu=xs_.dot(w), tau=beta, observed=ys)
means, _, elbos = pm.variational.advi(
model=model, n=1000, learning_rate=0.1, accurate_elbo=True)
w_post = means['w']
11](https://image.slidesharecdn.com/slide-160416103223/85/slide-11-320.jpg)
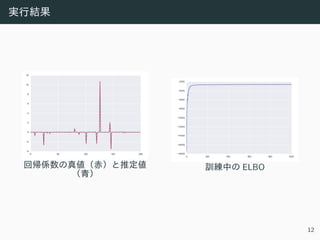
![コード例: Gaussian mixture model
• LogSumExp を⽤いて⽣成コンポーネントを表す確率変数を周辺
消去します.
• 尤度関数を記述すれば様々な混合分布をモデル化できます
(e.g., 正規分布+⼀様分布)
from pymc3.math import LogSumExp
# Log likelihood of normal distribution
def logp_normal(mu, tau, value):
# log probability of individual samples
k = tau.shape[0]
delta = lambda mu: value - mu
return (-1 / 2.) * (k * tt.log(2 * np.pi) + tt.log(1./det(tau)) +
(delta(mu).dot(tau) * delta(mu)).sum(axis=1))
# Log likelihood of Gaussian mixture distribution
def logp_gmix(mus, pi, tau):
def logp_(value):
logps = [tt.log(pi[i]) + logp_normal(mu, tau, value)
for i, mu in enumerate(mus)]
return tt.sum(LogSumExp(tt.stacklists(logps)[:, :n_samples], axis=0))
return logp_
13](https://image.slidesharecdn.com/slide-160416103223/85/slide-13-320.jpg)
![コード例(続き)および実⾏結果
• DensityDist() を使って様々な尤度関数を定義できます.
with pm.Model() as model:
mus = [MvNormal('mu_%d' % i, mu=np.zeros(2), tau=0.1 * np.eye(2), shape=(2,)
for i in range(2)]
pi = Dirichlet('pi', a=0.1 * np.ones(2), shape=(2,))
xs = DensityDist('x', logp_gmix(mus, pi, np.eye(2)), observed=data)
• ミニバッチを使うことで⼤量データに対する推定も可能です.
100,000 サンプルに対する GMM の平均推定結果.
14](https://image.slidesharecdn.com/slide-160416103223/85/slide-14-320.jpg)
![コード例: Latent Dirichlet Allocation (LDA)
• PyMC3 のバックエンドである Theano の機能を使って,
スパース⾏列として与えられたデータから対数尤度を計算でき
ます.
def logp_lda_f2(phi, thetas):
def ll_docs_f(tfs):
dixs, vixs = tfs.nonzero()
vfreqs = tfs[dixs, vixs]
ll_docs = vfreqs * LogSumExp(
tt.log(thetas[dixs] + 1e-10) + tt.log(phi[vixs] + 1e-10), axis=1).ra
return tt.sum(ll_docs)
return ll_docs_f
with pm.Model() as model:
thetas = pm.Dirichlet('thetas', a=1.0 * np.ones((n_topics, n_samples)), shap
phi = pm.Dirichlet('phi', a=1.0 * np.ones((n_features, n_topics)), shape=(n_
doc = pm.DensityDist('doc', logp_lda_f2(phi, thetas.T), observed=tfs.toarray
15](https://image.slidesharecdn.com/slide-160416103223/85/slide-15-320.jpg)

![変分ベイズ法 (1/2)
事後分布 p(X|D) を適当な分布 q(X) で近似して, 真の事後分布との
KL ダイバージェンス KL(q(X)||p(X|D)) に近づけます.
変分下限
周辺尤度 log p(D) = log
∫
p(D, X)dX と KL ダイバージェンスの間に
次の関係が成り⽴ちます:
log p(D) = L[q(X)] + KL(q(X)||p(X|D))
L[q(X)] ≡ Eq(X)[log p(D, X) − log q(X)]
KL(·||·) ≥ 0 より log L[q(X)] ≤ log p(D), つまり L[q(X)] は周辺尤度
の下限であり, Evidence lower bound (ELBO) と呼ばれます
([HBW+13]).
17](https://image.slidesharecdn.com/slide-160416103223/85/slide-17-320.jpg)

![確率的変分ベイズ法 (1/2)
q(X) に任意の分布を使うため, q(X) を θ でパラメトライズされる
分布族とし, ELBO に対して勾配法を適⽤します.
ELBO のパラメータに関する勾配 ∇θL[q(X)] を計算する⽅法として,
次の⼆つがあります ([TL15]):
1. Log-derivative trick: ∇θq(X) = q(X)∇θ log q(X) を利⽤します.
2. Reparametrization trick: パラメータを持たない分布 q(Z) と変数
変換 X = g(Z; θ) で q(X) を表現し, q(X) に関する期待値を (パ
ラメータを持たない) q(Z) に関する期待値に置き換えます.
いずれの場合も, 勾配を期待値として計算できます:
∇θL[q(X)] = Eq(X)[f(X)]
(あるいは Eq(Z)[f(Z)])
19](https://image.slidesharecdn.com/slide-160416103223/85/slide-19-320.jpg)
![確率的変分ベイズ法 (2/2)
確率的勾配勾配の式に現れる期待値計算のモンテカルロ積分による
近似:
˜∇θL[q(X)] =
1
M
M∑
m=1
f(Xm
), X ∼ q(X)
確率近似法適切にスケジューリングされた学習係数 ηt
⽤いて
パラメータを確率的に更新:
θ(t+1)
← θ(t)
+ η(t+1) ˜∇
(t+1)
θ L[q(X)]
確率的勾配の期待値が真の勾配に⼀致 ⇒ 最適解に収束 ([RM51])
このような確率的最適化に基づく事後分布推定を確率的変分ベイズ
法 (stochastic variational inference; SVI) と呼びます.
20](https://image.slidesharecdn.com/slide-160416103223/85/slide-20-320.jpg)
![注意
「確率的」の意味
ここでは期待値計算をサンプリングで確率的に近似する⽅法を説明
しました.
⼀⽅, ⽬的関数の計算でデータ D のサブサンプリング (ミニバッチ)
を
⽤いた⼿法も確率的変分ベイズ法と呼ばれます ([HBW+13]).
期待値とデータのサンプリングの両⽅を組み合わせたものは
⼆重確率変分ベイズ法とも呼ばれます ([TL14]).
21](https://image.slidesharecdn.com/slide-160416103223/85/slide-21-320.jpg)
![参考⽂献
• [BT00] Bishop, C. M., & Tipping, M. E. (2000, June). Variational relevance
vector machines. In Proceedings of the Sixteenth conference on Uncertainty in
artificial intelligence (pp. 46-53). Morgan Kaufmann Publishers Inc.. ARD の変
⽂ベイズ版.
• [TL14] Titsias, M., & Lázaro-Gredilla, M. (2014). Doubly stochastic variational
Bayes for non-conjugate inference. In Proceedings of the 31st International
Conference on Machine Learning (ICML-14) (pp. 1971-1979). 期待値のサンプリ
ングとデータのサンプリングを組み合わせた⼿法.
• [HBW+13] Hoffman, M. D., Blei, D. M., Wang, C., & Paisley, J. (2013).
Stochastic variational inference. The Journal of Machine Learning Research,
14(1), 1303-1347. データのサンプリングによって変分ベイズ法を⼤規模データ
に適⽤する⼿法.
• [RM51] Robbins, H., & Monro, S. (1951). A stochastic approximation method.
The annals of mathematical statistics, 400-407. 確率近似法.
• [TL15] Titsias, M., & Lázaro-Gredilla, M. (2015). Local Expectation Gradients
for Black Box Variational Inference. In Advances in Neural Information
Processing Systems (pp. 2620-2628). MC サンプリングを求積法に置き換えた⼿
法.
• [KRG+15] Kucukelbir, A., Ranganath, R., Gelman, A., & Blei, D. (2015).
Automatic variational inference in stan. In Advances in Neural Information
Processing Systems (pp. 568-576). ADVI とその Stan 実装の解説.
22](https://image.slidesharecdn.com/slide-160416103223/85/slide-22-320.jpg)