More Related Content
PPTX
PDF
PDF
PDF
サポートベクターマシン(SVM)の数学をみんなに説明したいだけの会 PDF
PDF
機械学習チュートリアル@Jubatus Casual Talks PDF
PDF
トピックモデルの評価指標 Perplexity とは何なのか? What's hot
PDF
PPTX
PPTX
PDF
相関と因果について考える:統計的因果推論、その(不)可能性の中心 PDF
PDF
PDF
PPTX
猫でも分かるVariational AutoEncoder PDF
Word Tour: One-dimensional Word Embeddings via the Traveling Salesman Problem... PDF
PDF
PDF
PPTX
PDF
PDF
PDF
PDF
PPTX
PDF
PDF
Similar to 確率的バンディット問題
PDF
多腕バンディット問題: 定式化と応用 (第13回ステアラボ人工知能セミナー) PDF
いろんなバンディットアルゴリズムを理解しよう PDF
PDF
公平性を保証したAI/機械学習
アルゴリズムの最新理論 PPTX
MLP輪読会 バンディット問題の理論とアルゴリズム 第3章 PDF
L 05 bandit with causality-公開版 PPTX
Pydata_リクルートにおけるbanditアルゴリズム_実装前までのプロセス PPTX
PPTX
PPTX
PDF
PPTX
Pycon reject banditアルゴリズムを用いた自動abテスト PPTX
PDF
PDF
Ml professional bandit_chapter1 PDF
Large-Scale Bandit Problems and KWIK Learning PDF
強化学習勉強会・論文紹介(第30回)Ensemble Contextual Bandits for Personalized Recommendation PDF
finite time analysis of the multiarmed bandit problem PDF
Reliability and learnability of human bandit feedback for sequence to-seque... PDF
More from jkomiyama
PPTX
PDF
Optimal Regret Analysis of Thompson Sampling in Stochastic Multi-armed Bandit... PDF
Annals of Statistics読み回 第一回 PPTX
PDF
PDF
確率的バンディット問題
- 1.
- 2.
- 3.
- 4.
- 5.
確率的バンディット問題
アーム数: 𝐾, ラウンド数:𝑇
予測者(システム)は各ラ
ウンド 𝑡=1,2,…Tに、アーム
𝐼𝑡 ∈ {1, . . , 𝐾}を選択し、報
酬𝑋𝐼 𝑡 𝑡 を受け取る.
目的: 総報酬の最大化
Maximize 𝑡=1
𝑇
𝑋𝐼 𝑡 (𝑡)
5
(image from
http://www.directgamesroom.com )
arm
- 6.
- 7.
- 8.
- 9.
バンディット問題の最適戦略
各アームの期待報酬を 𝜇1 >𝜇2 > 𝜇3 > ⋯ > 𝜇 𝐾とす
る(注. アルゴリズムはこの順番を知らない)
もし{𝜇𝑖}を全て知っているなら
→常に𝜇1を選び続けるのが最善
Tラウンドでの期待累計報酬=𝜇1 𝑇
・実際は各アームの期待報酬を知らないので、それ
ぞれの期待報酬を類推しながらアームを選んでいく
必要がある
9
- 10.
探索と活用のトレードオフ
探索:全アームを均等に調べる
→𝜇1, … ., 𝜇 𝐾を正確に推定したい
活用:一番良いアームを選びたい
→アームの報酬予測を{ 𝜇𝑖}とすると、argmaxi 𝜇𝑖を引く
→高い確率でargmaxi 𝜇𝑖 = 𝜇1だが、稀にそれ以外のアー
ムがたまたま良いように見えてしまうことがある
良いアルゴリズム=探索と活用をバランスできるアルゴ
リズム
10
- 11.
- 12.
- 13.
- 14.
- 15.
Cramer-Chernoffの定理
確率分布𝜇𝑖の推定値 𝜇𝑖 =
1
𝑁(𝑖)𝑠=1
𝑁(𝑖)
𝑋𝑖,𝑠 に対して
Pr 𝜇𝑖 > 𝑎 ≤ exp −𝑁 𝑖 sup
𝜃
𝜃𝑎 − 𝜆 𝜃 ,
where 𝜆 𝜃 = 𝑙𝑜𝑔𝐸[exp 𝜃𝑋𝑖],
Bernoulli分布なら sup
𝜃
𝜃𝑎 − 𝜆 𝜃 = 𝑑 𝜇𝑖, 𝑎 なので
以下のChernoffのバウンドが得られる
Pr 𝜇𝑖 > 𝜇1 ≤ exp(−𝑁(𝑖)𝑑 𝜇𝑖, 𝜇1 )
15
- 16.
- 17.
- 18.
- 19.
- 20.
UCB1のregret
アームを引く数:𝐸 𝑁 𝑇𝑖 ≤
8log(𝑇)
𝜇1−𝜇 𝑖
2
Regret:
𝐸 𝑅 𝑖 =
𝑖≠1
(𝜇1 − 𝜇𝑖)𝐸 𝑁 𝑇 𝑖 ≤
𝑖≠1
8log(𝑇)
(𝜇1 − 𝜇𝑖)
UCB1はRegretがO(log 𝑇 )のアルゴリズム
20
- 21.
UCB1のregret
(再掲)𝐸 𝑁 𝑇𝑖 ≤
8log(𝑇)
𝜇1−𝜇 𝑖
2
Pinskerの不等式 𝑑 𝑝, 𝑞 ≥ 2 𝜇1 − 𝜇𝑖
2により
8log(𝑇)
𝜇1 − 𝜇𝑖
2
≥
16 log 𝑇
𝑑 𝜇𝑖, 𝜇1
>
log 𝑇
𝑑(𝜇𝑖, 𝜇1)
というわけで、UCB1のregretはtightではない
これ以降紹介する3つのアルゴリズムは以下の点で最適
lim
𝑇→∞
𝐸 𝑁𝑖(𝑇) / log 𝑇 →
1
𝑑(𝜇𝑖, 𝜇1)
21
- 22.
DMED (Deterministic MinimumEmpirical Divergence)
[Honda&Takemura 2010]
アームiの経験分布 𝐹𝑖と一番経験平均が高いアー
ムの経験平均 𝜇𝑖∗の間のKL divergenceが
𝑑 𝐹𝑖, 𝜇𝑖∗ ≤ log 𝑡 /𝑇𝑖(𝑡)程度のアームを「最適で
ある可能性があるアームのリスト」として持つ
𝑑 𝐹𝑖, 𝜇𝑖∗ は双対問題𝑑′ 𝐹𝑖, 𝜇𝑖∗ が数値的に (e.g.
Newton法、二分法)解けて、双対問題の解と主
問題の解が一致
22
- 23.
KL-UCB [Garivier+ 2011]
UCBの信頼上限をKLdivergenceをもとに厳密化
各ラウンドで、次のKL-UCB indexが最大のアームを
選ぶ
𝐵 𝐾𝐿−𝑈𝐶𝐵 𝑖
= max
𝑞∈[ 𝜇 𝑖,1]
{𝑁𝑖 𝑑 𝜇𝑖, 𝑞 ≤ log 𝑡 + 3log(log 𝑡 )}
𝑢𝑖 = 𝜇𝑖からdivergenceがlog 𝑡 /𝑁𝑖 程度の値
・𝐵 𝐾𝐿−𝑈𝐶𝐵 𝑖 は数値的に解ける
・3log(log 𝑡 )項は理論的な産物(実際必要かどうか
は不明)
23
- 24.
Thompson sampling [Thompson1933]
Bayes推定+Posterior sampling
1. 各アームiの報酬の確率分布を初期化(𝛼𝑖 = 1, 𝛽𝑖 = 1)
2. 各ラウンドで確率分布のposteriorからサンプルし、そのサンプルの最大
なものを選ぶ
𝜃𝑖 ∼ 𝐵𝑒𝑡𝑎(𝛼𝑖, 𝛽𝑖), and 𝐼 𝑡 =argmax 𝜃𝑖
3. 報酬を見て確率分布を更新
If 𝑋𝐼 𝑡 𝑡 =1 then 𝛼𝑖=𝛼𝑖+1 else 𝛽𝑖=𝛽𝑖+1
太古から知られているアルゴリズムだが、最適性の証明はごく最近
[Agrawal&Goyal 2011, Kaufmann+2012]
24
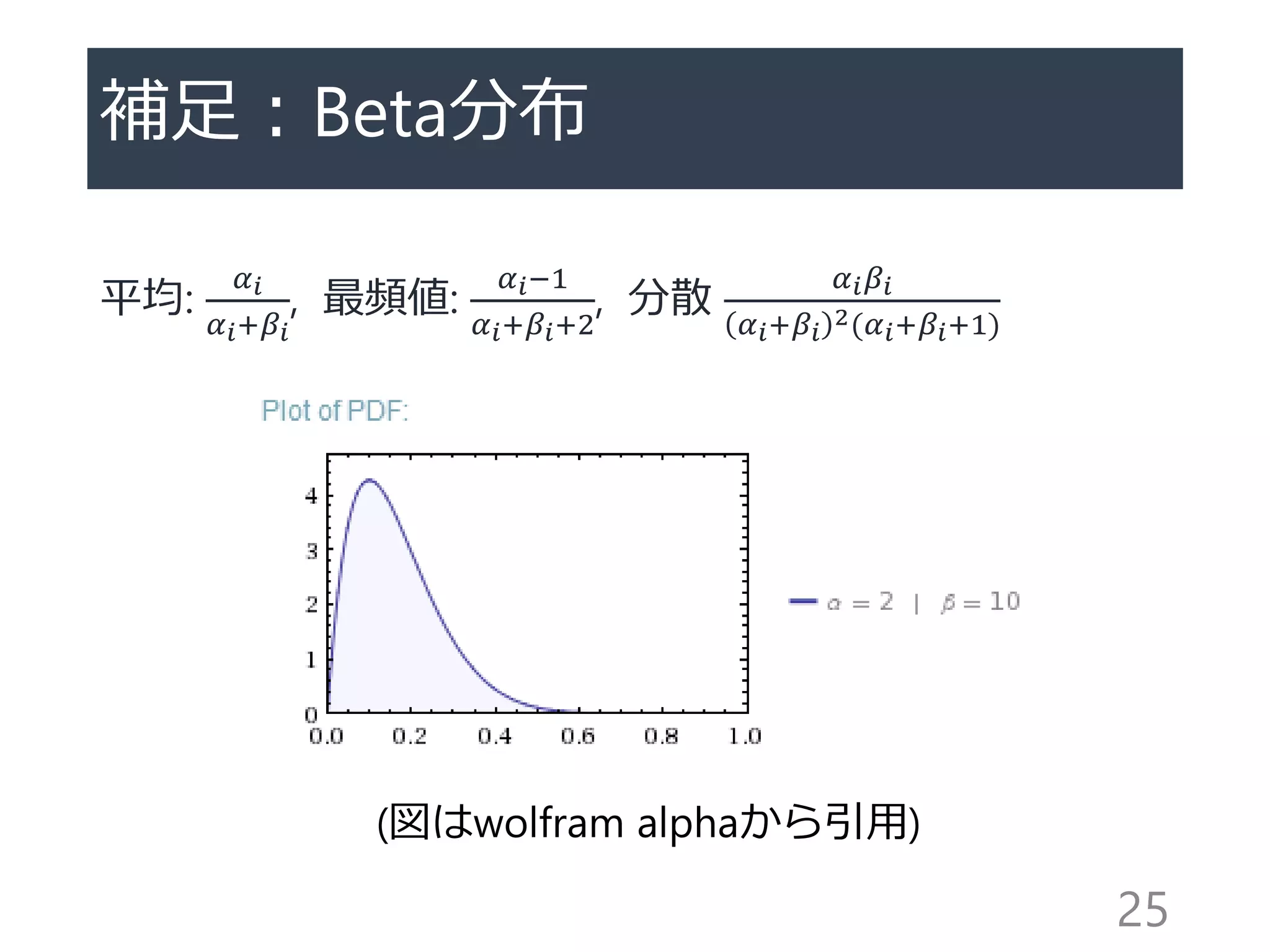
- 25.
- 26.
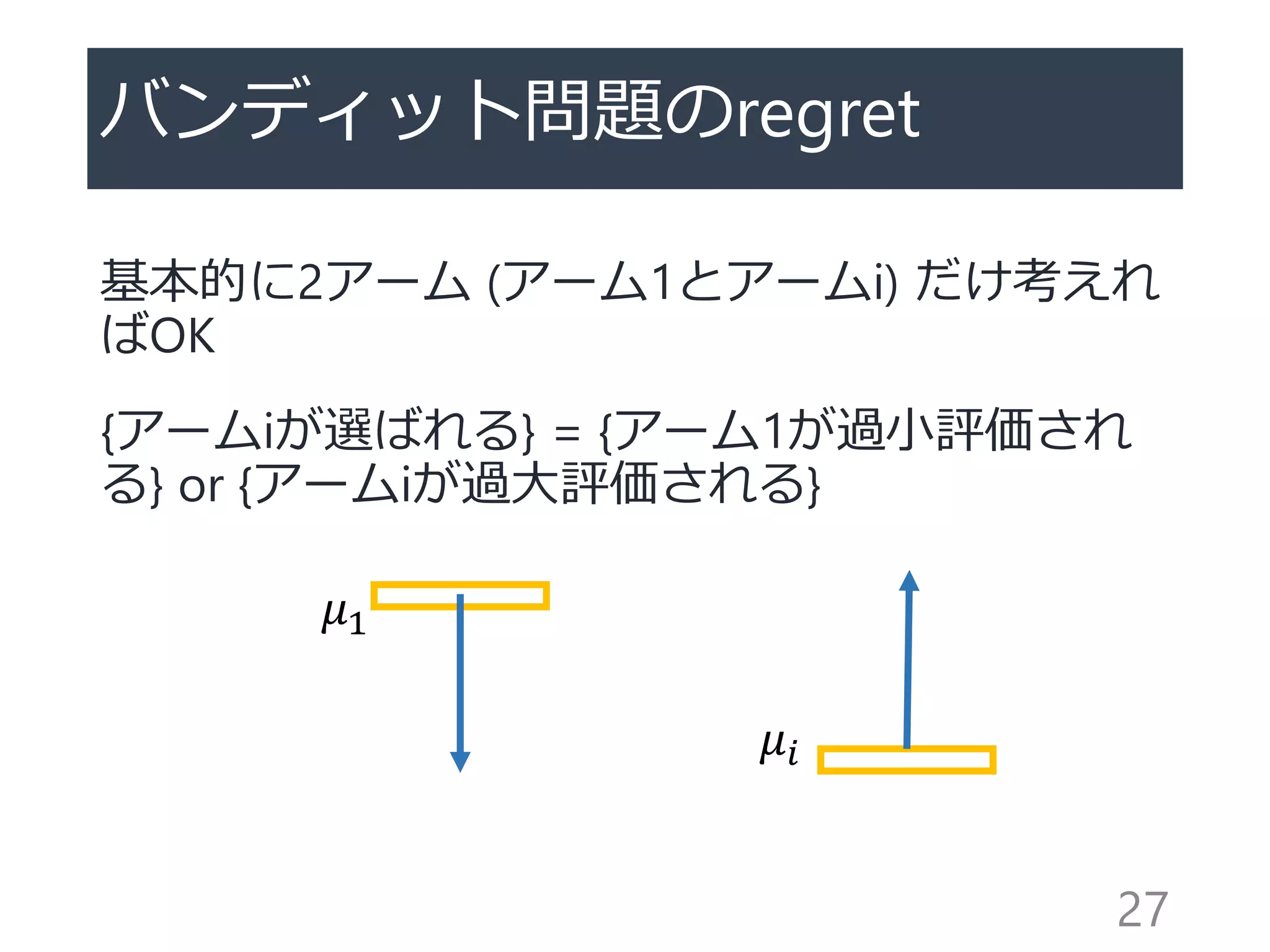
- 27.
- 28.
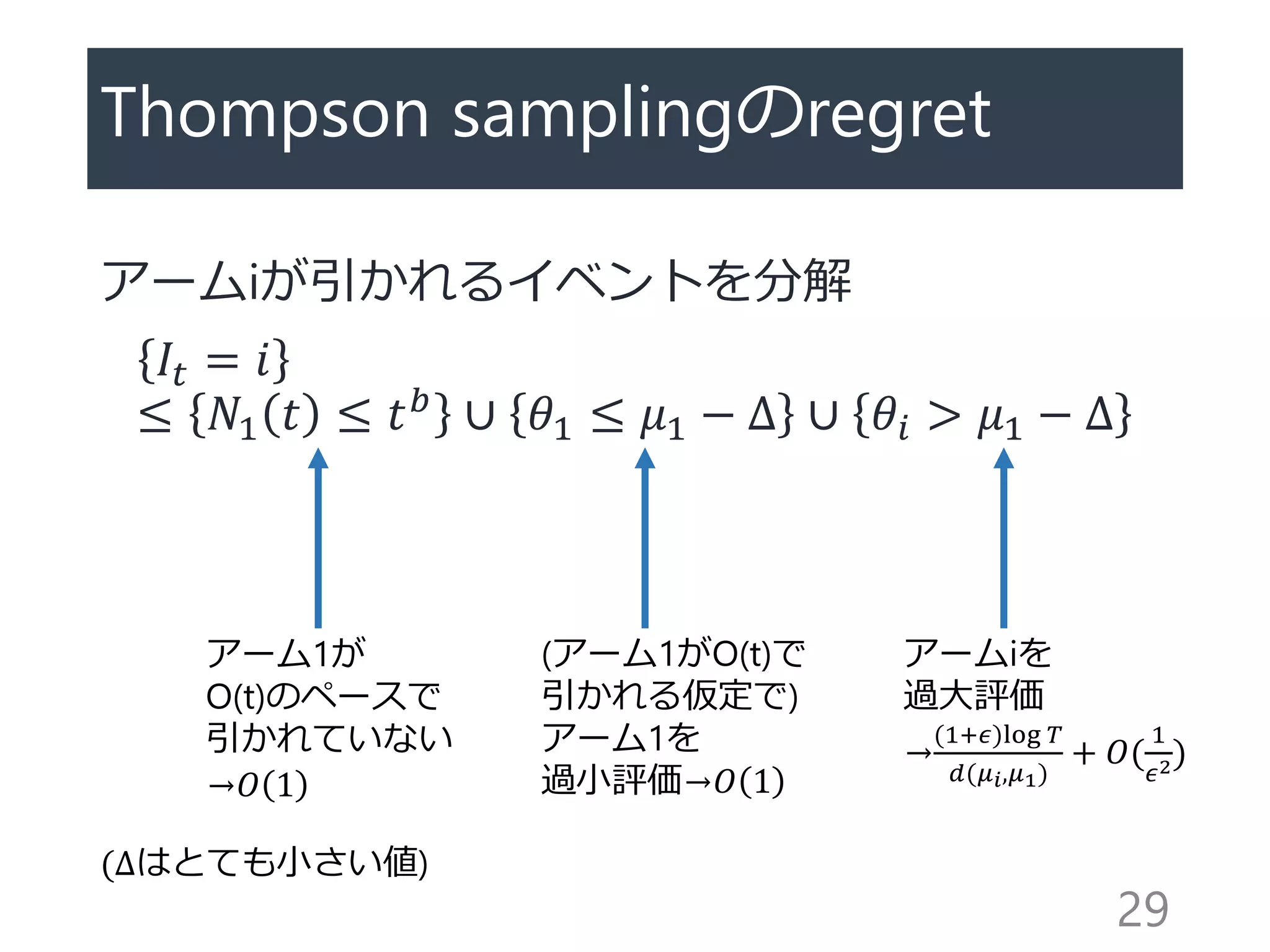
- 29.
- 30.










![Regret (評価手法)
最適なアーム選択(=𝜇1を毎回選ぶ)とアルゴ
リズムの選択の差
𝑅𝑒𝑔𝑟𝑒𝑡 𝑇 = 𝜇1 𝑇 −
𝑖
𝐾
𝜇𝑖 𝑁 𝑇 (𝑖)
アルゴリズムの目標
→𝐸 𝑅𝑒𝑔𝑟𝑒𝑡 𝑇 の最小化(小さいほど良い)
→最適でないアームを引く数𝐸[𝑁𝑖(𝑇)]の最小化
11](https://image.slidesharecdn.com/presenkomiyamastochasticbandit-140517044317-phpapp01/75/slide-11-2048.jpg)

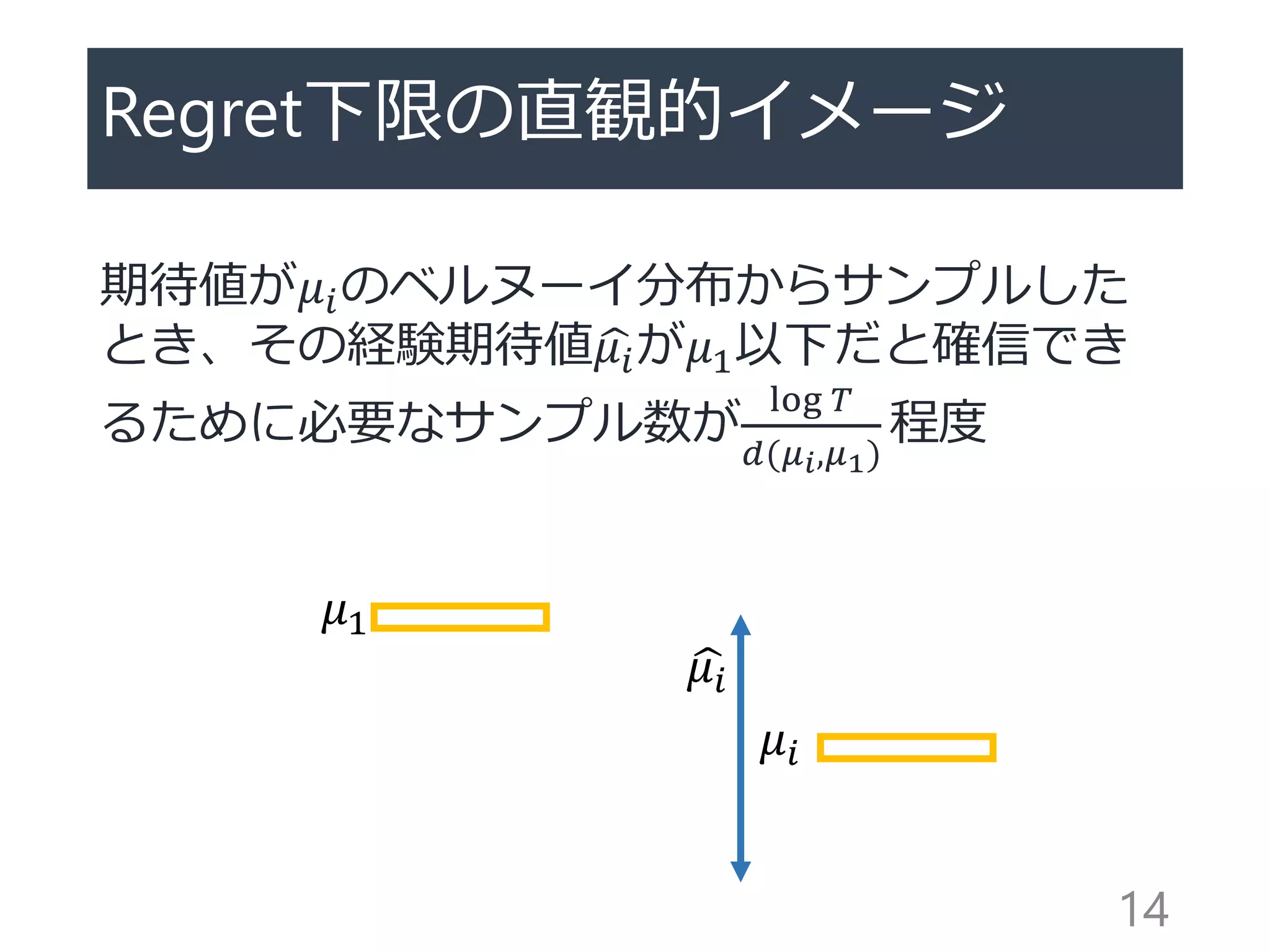
![Regret下限 [Lai&Robbins 1985]
強一致性を持つ(任意のアーム集合と𝛼 > 0に対
してregretが𝑜(𝑇 𝛼)になる)アルゴリズムに関し
て
𝐸 𝑁𝑖(𝑇) ≥
log 𝑇
𝑑(𝜇𝑖, 𝜇1)
この下限と一致する満たすアルゴリズムが最適
なアルゴリズム
・𝑜(log 𝑇 )な項は無視
13](https://image.slidesharecdn.com/presenkomiyamastochasticbandit-140517044317-phpapp01/75/slide-13-2048.jpg)
![Cramer-Chernoffの定理
確率分布𝜇𝑖の推定値 𝜇𝑖 =
1
𝑁(𝑖) 𝑠=1
𝑁(𝑖)
𝑋𝑖,𝑠 に対して
Pr 𝜇𝑖 > 𝑎 ≤ exp −𝑁 𝑖 sup
𝜃
𝜃𝑎 − 𝜆 𝜃 ,
where 𝜆 𝜃 = 𝑙𝑜𝑔𝐸[exp 𝜃𝑋𝑖],
Bernoulli分布なら sup
𝜃
𝜃𝑎 − 𝜆 𝜃 = 𝑑 𝜇𝑖, 𝑎 なので
以下のChernoffのバウンドが得られる
Pr 𝜇𝑖 > 𝜇1 ≤ exp(−𝑁(𝑖)𝑑 𝜇𝑖, 𝜇1 )
15](https://image.slidesharecdn.com/presenkomiyamastochasticbandit-140517044317-phpapp01/75/slide-15-2048.jpg)



![アルゴリズム: UCB1 [Auer+2002]
各アームに次のUCB1 indexを設定し、各ラウン
ドで最大indexのアームを選択する
𝐵 𝑈𝐶𝐵 𝑖 = 𝜇𝑖 +
2log(𝑇)
𝑁 𝑖(𝑡)
経験期待値(活用)+あまり引いていないアー
ムの不確定性(探索)
19
活用 探索](https://image.slidesharecdn.com/presenkomiyamastochasticbandit-140517044317-phpapp01/75/slide-19-2048.jpg)


![DMED (Deterministic Minimum Empirical Divergence)
[Honda&Takemura 2010]
アームiの経験分布 𝐹𝑖と一番経験平均が高いアー
ムの経験平均 𝜇𝑖∗の間のKL divergenceが
𝑑 𝐹𝑖, 𝜇𝑖∗ ≤ log 𝑡 /𝑇𝑖(𝑡)程度のアームを「最適で
ある可能性があるアームのリスト」として持つ
𝑑 𝐹𝑖, 𝜇𝑖∗ は双対問題𝑑′ 𝐹𝑖, 𝜇𝑖∗ が数値的に (e.g.
Newton法、二分法)解けて、双対問題の解と主
問題の解が一致
22](https://image.slidesharecdn.com/presenkomiyamastochasticbandit-140517044317-phpapp01/75/slide-22-2048.jpg)
![KL-UCB [Garivier+ 2011]
UCBの信頼上限をKL divergenceをもとに厳密化
各ラウンドで、次のKL-UCB indexが最大のアームを
選ぶ
𝐵 𝐾𝐿−𝑈𝐶𝐵 𝑖
= max
𝑞∈[ 𝜇 𝑖,1]
{𝑁𝑖 𝑑 𝜇𝑖, 𝑞 ≤ log 𝑡 + 3log(log 𝑡 )}
𝑢𝑖 = 𝜇𝑖からdivergenceがlog 𝑡 /𝑁𝑖 程度の値
・𝐵 𝐾𝐿−𝑈𝐶𝐵 𝑖 は数値的に解ける
・3log(log 𝑡 )項は理論的な産物(実際必要かどうか
は不明)
23](https://image.slidesharecdn.com/presenkomiyamastochasticbandit-140517044317-phpapp01/75/slide-23-2048.jpg)
![Thompson sampling [Thompson 1933]
Bayes推定+Posterior sampling
1. 各アームiの報酬の確率分布を初期化(𝛼𝑖 = 1, 𝛽𝑖 = 1)
2. 各ラウンドで確率分布のposteriorからサンプルし、そのサンプルの最大
なものを選ぶ
𝜃𝑖 ∼ 𝐵𝑒𝑡𝑎(𝛼𝑖, 𝛽𝑖), and 𝐼 𝑡 =argmax 𝜃𝑖
3. 報酬を見て確率分布を更新
If 𝑋𝐼 𝑡 𝑡 =1 then 𝛼𝑖=𝛼𝑖+1 else 𝛽𝑖=𝛽𝑖+1
太古から知られているアルゴリズムだが、最適性の証明はごく最近
[Agrawal&Goyal 2011, Kaufmann+2012]
24](https://image.slidesharecdn.com/presenkomiyamastochasticbandit-140517044317-phpapp01/75/slide-24-2048.jpg)