More Related Content
PDF
[PRML] パターン認識と機械学習(第2章:確率分布) PPTX
PPTX
PDF
PDF
PPTX
PDF
PDF
What's hot
PDF
PDF
PRML上巻勉強会 at 東京大学 資料 第1章前半 PDF
PDF
PDF
PDF
PDF
PRML上巻勉強会 at 東京大学 資料 第1章後半 PPTX
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
Prml4.4 ラプラス近似~ベイズロジスティック回帰 PPTX
PDF
Similar to パターン認識と機械学習(PRML)第2章 確率分布 2.3 ガウス分布
PDF
PDF
[PRML] パターン認識と機械学習(第1章:序論) PDF
PDF
PDF
Prml 1.2,4 5,1.3|輪講資料1120 PDF
PDF
PRML上巻勉強会 at 東京大学 資料 第2章2.3.3 〜 2.5.2 PPT
PDF
PRML上巻勉強会 at 東京大学 資料 第2章2.3.3 〜 2.3.6 PPTX
PDF
PDF
Pattern Recognition and Machine Learning study session - パターン認識と機械学習 勉強会資料 PDF
PDF
PRML 10.3, 10.4 (Pattern Recognition and Machine Learning) PDF
PDF
PDF
14.05.25 大阪PRML読書会 第2章 2.3.3-2.3.6 (pp.88-100) PDF
PRML2.3.8~2.5 Slides in charge PDF
PRML_titech 2.3.1 - 2.3.7 PDF
Recently uploaded
PDF
2025→2026宙畑ゆく年くる年レポート_100社を超える企業アンケート総まとめ!!_企業まとめ_1229_3版 PDF
第21回 Gen AI 勉強会「NotebookLMで60ページ超の スライドを作成してみた」 PDF
100年後の知財業界-生成AIスライドアドリブプレゼン イーパテントYouTube配信 PDF
さくらインターネットの今 法林リージョン:さくらのAIとか GPUとかイベントとか 〜2026年もバク進します!〜 PDF
Starlink Direct-to-Cell (D2C) 技術の概要と将来の展望 PDF
Reiwa 7 IT Strategist Afternoon I Question-1 3C Analysis PDF
Reiwa 7 IT Strategist Afternoon I Question-1 Ansoff's Growth Vector PDF
PPTX
パターン認識と機械学習(PRML)第2章 確率分布 2.3 ガウス分布
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
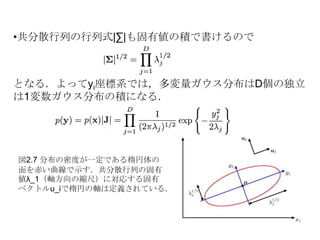
(2.70)の線形項( の関係を利用する)と (2.71)の線形項とを比較して,(2.75)これらの式から,ガウス分布の条件分布の平均は,xの線形関数で,共分散はxとは独立であることが分かる.15 - 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.