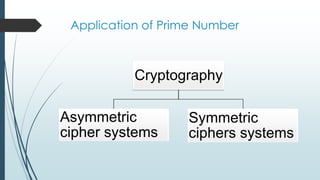
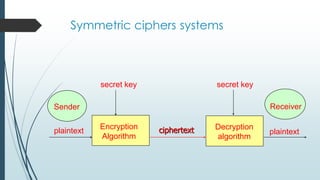
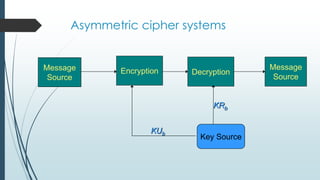
The document discusses prime numbers, defining them as integers greater than one with only 1 and itself as factors, and exploring their applications in nature and cryptography. It highlights the significance of prime numbers in the cicada lifecycle and details their role in encryption methods like RSA. The document concludes with the concept of Mersenne primes and the importance of prime numbers in mathematics and security.

1. What is Prime Numbers?
By Mhd Imran CHAMIEH

2. Outline
• Prime number definition
• Example from real life
• Cryptography
• Prime number form
• Conclusion

3. Definition
• Prime Number – An integer bigger than one
whose only factors are 1 and itself
• The first 25 prime number
• 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,
61,67,71,73,79,83,89,97,….

4. Prime numbers in nature

5. Prime numbers in natural
• The usage of prime number in natural selection is
shown in Cicada lifecycle that may be periods of
either 17 or 13 years, which are prime numbers
that in necessarily will trick the predators to predict
and synchronize its lifecycle with Cicada`s

6. Application of Prime Number
Cryptography
Asymmetric
cipher systems
Symmetric
ciphers systems

7. Symmetric ciphers systems
ciphertext
secret key secret key
plaintextplaintext
Sender
Decryption
algorithm
Encryption
Algorithm
Receiver

8. Asymmetric cipher systems
Message
Source
Encryption Message
Source
Decryption
Key Source
KUb
KRb

9. One Way Function(OWF)
• A One-Way Function is a function that is "easy"
to compute and "difficult" to reverse
• Examples of OWF to explain public-key systems
• Multiplication of two primes
• Modular exponentiation

10. OWF: Modular Exponentiation
• The process of exponentiation just means raising numbers
to a power
• Raising a to the power b, normally denoted ab just means
multiplying a by itself b times. In other words
ab = a *a * a * … a
• Modular exponentiation means computing ab modulo
some other number n. We write this as ab mod n
• Modular exponentiation is "easy"

11. OWF: Modular Exponentiation
• However, given a is an integer , then the equation
ab mod n (when n is prime), finding b is regarded by
mathematicians as a hard problem
• In other words, given a number a and a prime number n,
the function
f(b) = ab mod n
is believed to be a one-way function

12. RSA
• It is named after it inventors Ron Rivest, Adi
Shamir and Len Adleman.
• Published in 1978
• It is the most widely used public-key encryption
algorithm today
• It provides confidentiality and digital signatures
• Its security is based on the difficulty of integer
factorization

13. Example: Confidentiality
• Generate two large (at least 512 bits) primes p and q
• Take p = 7, q = 11
• Compute n=pq and (n)=(p-1)(q-1) .
• so n = 77 and (77) =(7-1)(11-1)= 60
• Choose e < (n) relatively prime to (n) (i.e. gcd (e, 60)=1)
• Say I choose (KUb) e = 17
• 17 x d mod 60 = 1 (KRb) d = 53

14. Example: Confidentiality
• A’s Public key: (e, n) (17,77) // to be published.
• A’s private key: d (or (d, n)) (53,77)// to be kept
secretly by A

15. Example: Confidentiality
• Imran wants to secretly send Mhd the message "HELLO"
• H E L L O
• 08 05 12 12 15
• 0817 mod 77 = 57
• 0517 mod 77 = 03
• 1217 mod 77 = 45
• 1217 mod 77 = 45
• 1517 mod 77 = 71
• Imran sends ciphertext [57 3 45 45 71]

16. Example: Confidentiality


17. Attacking RSA
If the attacker knows the public key of a user (e,n) what
would she/he need to do in order to obtain the corresponding
private key?
• He/she needs to find d such that e.d mod (n) = 1
• i.e., needs to know p and q
• In other words, he/she must factor n (problem of prime
factorization)

18. Mersenne Prime Number Form
prime

19. Mersenne Prime Number Form


20. Mersenne Prime Number Form


21. Mersenne Prime Number Form


22. The largest Prime Number


23. Finally
Descartes 1596-1650
• "The universe is written in
Mathematical language"
math is based on numbers
and numbers are based
on primes

24. Conclusion
• Definition of prime number
• Cicada lifecycle and how protect it self
• Application of prime number in security
• Mersenne form of prime number
• The largest discovered prime number

25. The End
Imran.shamia@gmail.com
6/4/2014