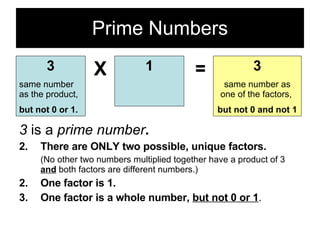
This document discusses prime numbers, composite numbers, and how to determine which category a whole number falls into. It provides that: - Prime numbers have exactly two unique factors - the number itself and 1. - Composite numbers have more than two factors. - Only the numbers 0, 1, and 2 are neither prime nor composite - 0 because every number divides it, and 1 because it only has one factor. All other whole numbers are either prime or composite.

1. Prime numbers Composite numbers Neither prime nor composite How to know?

2. Prime and composite numbers are all about multiplication Multiplication math vocabulary: The two numbers being multiplied together are each called factors . The answer in a multiplication problem is called the product .

3. Multiplication factor x factor = product

4. Prime Numbers To determine if a number is a prime number , place it in the product position. Product Is this number a prime number ? Factor X Factor =

5. Prime Numbers Must have ONLY two possible, unique factors. (Both factors cannot be the same.) One factor must be 1. One factor must be a whole number, but not 0 or 1 . Factor same number as the product, but not 0 or 1. X Factor 1 = Product same number as one of the factors, but not 0 and not 1

6. Whole numbers In case you forgot: Whole numbers are the the number 0, and the natural numbers which start at positive one— { 0, 1, 2, 3... }

7. Prime Numbers 3 is a prime number . There are ONLY two possible, unique factors. (No other two numbers multiplied together have a product of 3 and both factors are different numbers.) 2. One factor is 1. 3. One factor is a whole number, but not 0 or 1 . 3 same number as the product, but not 0 or 1. X 1 = 3 same number as one of the factors, but not 0 and not 1

8. Prime Numbers A common misconception is that odd numbers are always prime numbers but, that’s not true.

9. Prime Numbers Some odd numbers , like 9 have more than two factors . 9 x 1 = 9 , but so does 3 x 3 . Consequently, 9 is not a prime number.

10. Prime Numbers 51 is tricky! It is an odd number. It looks like only 51 x 1 = 51, but 17 x 3 = 51 too . 51 is not a prime number . HINT : Divisibility rules and multiplication tables can help you discover that a number that seems like a prime number really isn’t.

11. Prime Numbers However , even numbers are never prime numbers with one exception— the number 2 .

12. Prime Numbers 2 is a prime number , because the only two factors of 2 are 2 x 1 = 2. Every other even number has 2 as a factor too (that’s why no other even number is a prime number).

13. Composite Numbers Numbers with more than two factors are called composite numbers . Numbers that aren’t prime numbers are composite numbers.

14. The special case of the number 1 The number 1 is not a prime number and, it is not a composite number. Why ? because, the number 1 only has one factor , not two different factors . 1 x 1 = 1

15. The special case of the number 0. Zero is another special number. Zero can not be a prime number because, every number is a factor of 0 . 0 x 1 does equal 0, but 0 x anything at all = 0 Zero is not a composite number either.

16. Only 0 and 1 are neither prime nor composite numbers. All other whole numbers are either prime or composite numbers.

17. Congratulations! That’s how to tell a prime number from a composite number. Remember, if in doubt; with big numbers, use divisibility rules. With smaller products, use multiplication tables. And all even numbers, except 2, are always composite.

18. Notes for teachers on texts correlation: Correlates with Glencoe Mathematics (Florida Edition) texts: Mathematics: Applications and Concepts Course 1: (red book) Chapter 1 Lesson 3: Prime Factors Mathematics: Applications and Concepts Course 2: (blue book) Chapter 5 Lesson 1: Prime Factorization Pre-Algebra: (green book) Chapter 4 Lesson 3: Prime Factorization For more information on my math class see http:// walsh.edublogs.org

19. Notes for teachers on design This slide presentation was created using Microsoft Office PowerPoint 2003 part of Microsoft Office Standard Version for Students and Teachers. Finally, thank you. I hope this is of help to your students. Taleese