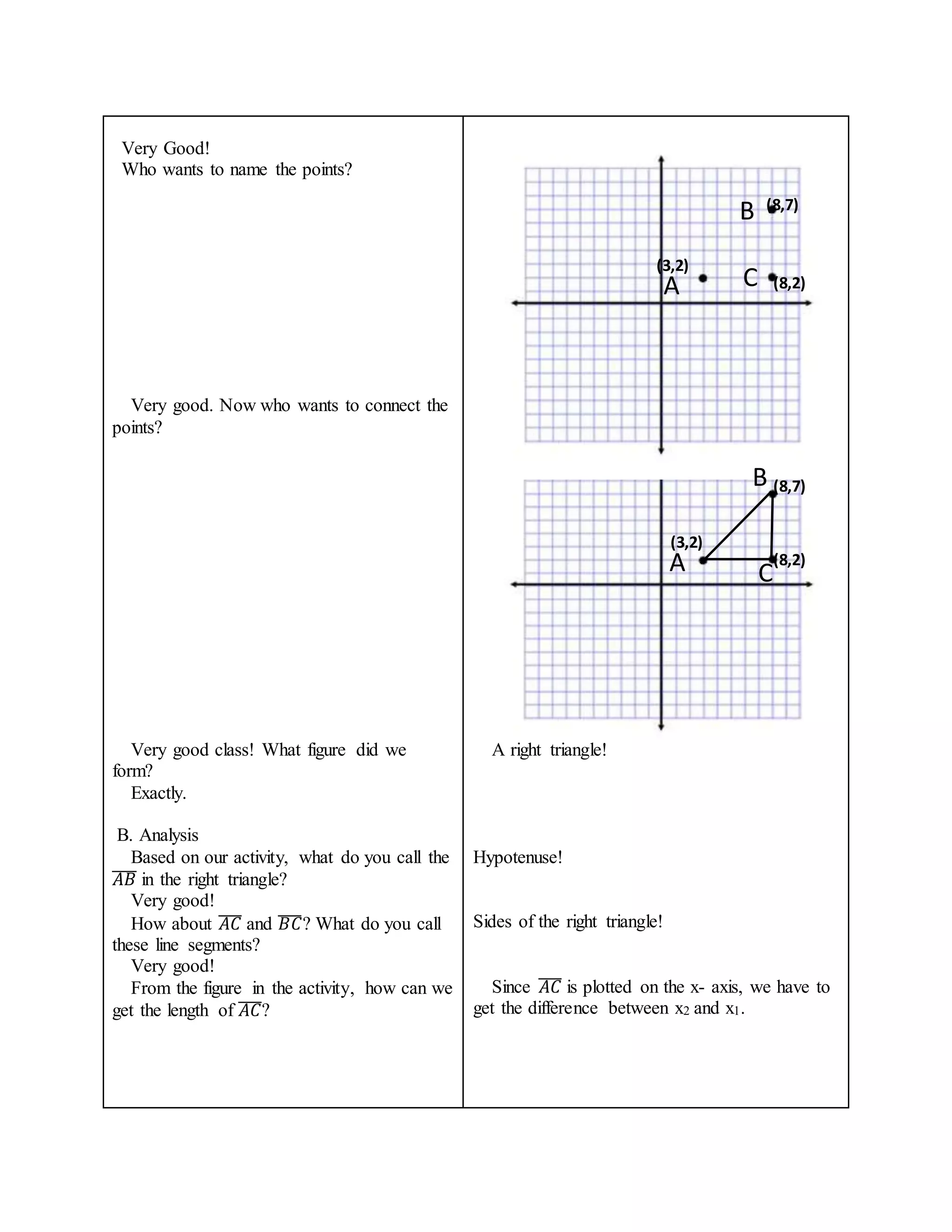
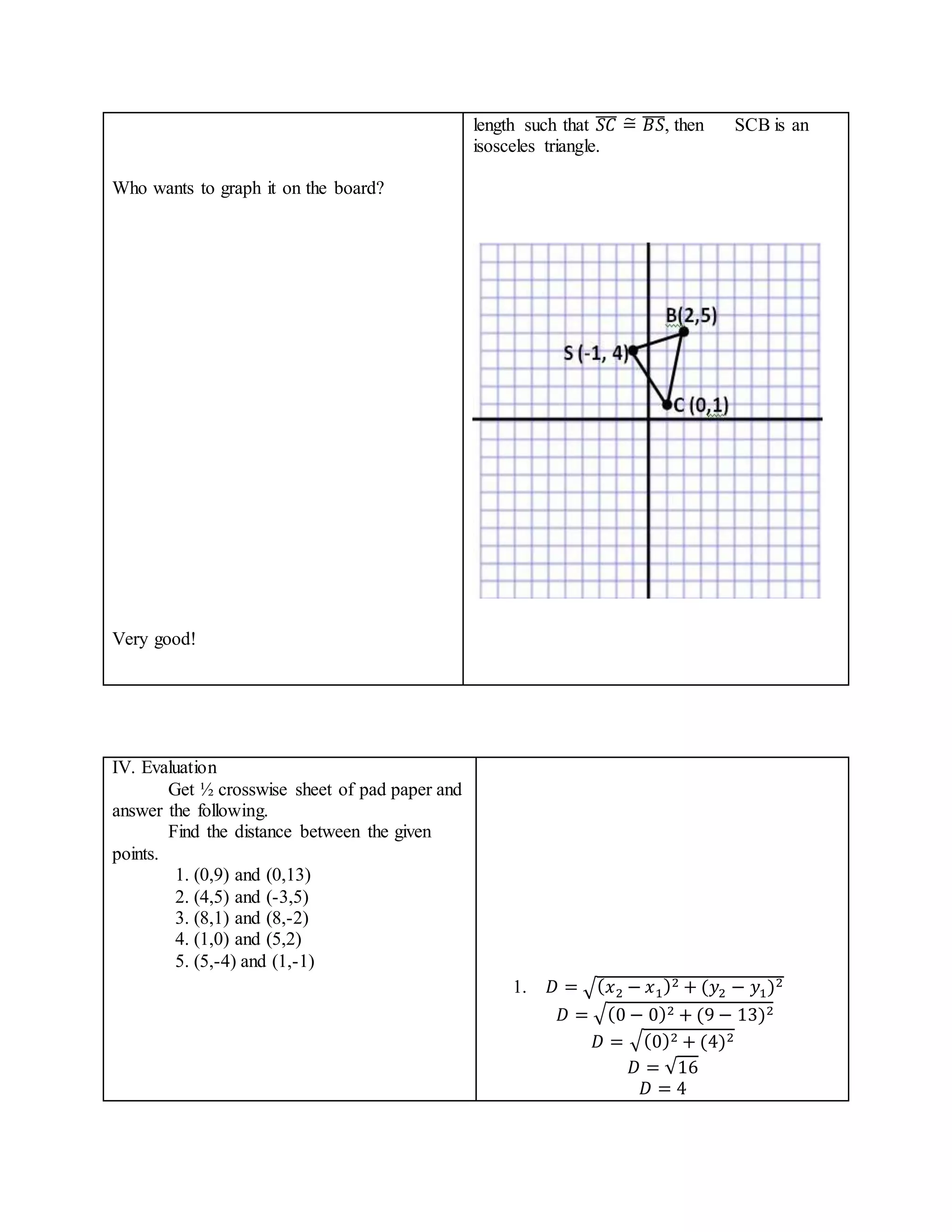
The document provides a learning plan for teaching students about the distance formula in mathematics. It includes objectives, subject matter, procedures for lessons and activities, and an evaluation. The teacher leads students in an activity to plot points and form a right triangle. They derive the distance formula by relating it to the Pythagorean theorem. Students then practice applying the distance formula to find distances between various point coordinates.

1. LEARNING PLAN IN MATHEMATICS
INSTRUCTIONAL SEQUENCES
I. Objectives:
At the end of the discussion, the students with at least 85% of mastery will be able to:
a. derive the distance formula;
b. solve the distance between two points by the use of distance formula;
c. relate Pythagorean Theorem to Distance Formula; and
d. show enthusiasm during class discussion.
II. Subject Matter
a. Topic: Distance Formula
b. Reference: Benes, Salita (2008). Painless Math Geometry. Anvil Publishing Inc.
pp. 118-119
III. Procedures:
Daily Routine
 Prayer
 Checking of Attendance
Teacher’s Activity
A. Activity
Before we proceed to our lesson proper for
the day. Let’s have an activity.
Plot these coordinates on our Cartesian
plane.
 (3,2)
 (8,7)
 (8,2)
Who wants to plot the coordinates?
Students’ Activity
(8,7)
(8,2)
(3,2)

2. Very Good!
Who wants to name the points?
Very good. Now who wants to connect the
points?
Very good class! What figure did we
form?
Exactly.
B. Analysis
Based on our activity, what do you call the
̅퐴̅̅퐵̅ in the right triangle?
Very good!
How about ̅퐴̅̅퐶̅ and ̅퐵̅̅퐶̅? What do you call
these line segments?
Very good!
From the figure in the activity, how can we
get the length of ̅퐴̅̅퐶̅?
A right triangle!
Hypotenuse!
Sides of the right triangle!
(3,2)
Since ̅퐴̅̅퐶̅ is plotted on the x- axis, we have to
get the difference between x2 and x1.
(8,7)
(8,2)
A
B
(3,2) C
(8,7)
(8,2)
A
B
C

3. Who wants to solve on the board?
Very good!
How about ̅퐵̅̅퐶̅? How can we get the length
of
̅퐵̅̅퐶̅?
Who wants to solve on the board?
Very Good!
Since we formed a right triangle,
what theorem we are going to use to find
the length of ̅퐴̅̅퐵̅ ?
Great!
Who can still remember the Pythagorean
Theorem and what is it?
Therefore, to find the length of ̅퐴̅̅퐵̅, we let
푐 = ̅퐴̅̅퐵̅ and ̅퐴̅̅퐵̅ is the hypotenuse of the right
triangle right class?
Now, let 푎= ̅퐴̅̅퐶̅ and 푏= ̅퐵̅̅퐶̅ ,since ̅퐴̅̅퐶̅= x2-x1
and ̅퐵̅̅퐶̅= y2-y1 then 푎 is equivalent to what?
Very good!
How about 푏?
What property of equality do you think did
we use?
Great Job!
x2=8, x1=3
x2-x1
= 8-3
= 5
Since ̅퐵̅̅퐶̅ is plotted on the y-axis, we have to
get the difference between y2 and y1.
y2=7, y1=2
y2 – y1
= 7-2
= 5
Sir, we are going to use the Pythagorean
Theorem.
The Pythagorean Theorem is
c2 = a2 + b2
√푐2 = √푎2 + 푏2
c = √푎2 + 푏2
Yes, sir!
푎= x2-x1
푏 = y2-y1
Transitive property

4. And now, who wants to substitute the
equivalent of a and b in the Pythagorean
theorem?
Exactly!
Since class we are finding the length of ̅퐴̅̅퐵̅
and the length of ̅퐴̅̅퐵̅ is the distance between
points A and B. Let 푐 = 퐷, thus,
퐷 = √(푥2 − 푥1)2 + (푦2 − 푦1)2
And now we have the distance formula.
Going back to our activity.
Through substitution method, who wants to
substitute the value in our distance formula?
C. Abstraction
Again what is the distance formula?
Very Good!
What is the connection between Pythagorean
Theorem and Distance Formula?
푐 = √(푥2 − 푥1)2 + (푦2 − 푦1 )2
We come up with, x2-x1 = 5, y2 – y1
= 5
By substitution: 퐷 =
√(푥2 − 푥1)2 + (푦2 − 푦1)2
퐷 = √(5)2 + (5)2
퐷 = √50
The Distance Formula is
퐷 = √(푥2 − 푥1)2 + (푦2 − 푦1)2
The Pythagorean Theorem States that
c2 = a2+b2
Where c is the length of the hypotenuse of the
right triangle and 푎is the horizontal leg, b is the
length of the vertical leg.
The Distance formula states that
퐷 = √(푥2 − 푥1)2 + (푦2 − 푦1)2
Where D is the Distance between two points,
(푥2 − 푥1) is the horizontal distance between two
points and (푦2 − 푦1 ) is the vertical distance
between two points.

5. D. Application
We are having an activity, first, group
yourself into 3. And answer the given
problem sets.
Graph and show that the following
coordinates forms an isosceles triangle by
using the distance formula.
S (-1,4)
C (0,1)
B (2,5)
You are given 10 minutes to answer it with
your assigned group members.
Ok class what made it an isosceles triangle?
̅푆̅̅퐶̅ = √(푥2− 푥1)2 + (푦2 − 푦1 )2
=√(−1 − 0)2 + (−4 − 1)2
=√(−1)2 + (−3)2
=√1 + 9
= √10
̅퐶̅̅퐵̅ = √(푥2 − 푥1)2 + (푦2 − 푦1 )2
=√(2 − 0)2 + (5−1)2
=√4 + 16
=√20
=5√2
̅퐵̅̅푆̅ = √(푥2 − 푥1)2 + (푦2 − 푦1)2
=√(2 + 1)2 + (5−4)2
=√10
Since there are two sides that has equivalent

6. IV. Evaluation
Get ½ crosswise sheet of pad paper and
answer the following.
Find the distance between the given
points.
1. (0,9) and (0,13)
2. (4,5) and (-3,5)
3. (8,1) and (8,-2)
4. (1,0) and (5,2)
5. (5,-4) and (1,-1)
1. 퐷 = √(푥2 − 푥1)2 + (푦2 − 푦1)2
퐷 = √(0 − 0)2 + (9 − 13)2
퐷 = √(0)2 + (4)2
퐷 = √16
퐷 = 4
Who wants to graph it on the board?
Very good!
length such that ̅푆̅̅퐶̅ =̃ ̅퐵̅̅푆̅, then SCB is an
isosceles triangle.

7. 2. 퐷 = √(푥2 − 푥1)2 + (푦2 − 푦1)2
퐷 = √(4 − (−3))2 + (5 − 5)2
퐷 = √(7)2 + (0)2
퐷 = √49
퐷 = 7
3. 퐷 = √(푥2 − 푥1)2 + (푦2 − 푦1)2
퐷 = √(8 − 8)2 + (1 − (−7))2
퐷 = √(0)2 + (8)2
퐷 = √64
퐷 = 8
4. 퐷 = √(푥2 − 푥1)2 + (푦2 − 푦1)2
퐷 = √(1 − 5)2 + (0 − 2)2
퐷 = √(−4)2 + (−2)2
퐷 = √16 + 4
퐷 = √20
퐷 = 5√2
5. 퐷 = √(푥2 − 푥1)2 + (푦2 − 푦1)2
퐷 = √(5 − 1)2 + ((−4) − (−1))2
퐷 = √(4)2 + (−3)2
퐷 = √16 + 9
퐷 = √25
퐷 = 5
V. Closure
In your assignment notebook, answer the following:
A. Graph and Find the distance using distance formula.
I (-4,6) and V (2,5)
Y (-1,6) and S (5, 10)
B. Make a research on midpoint and give at least 2 examples.