Dokumen ini membahas konsep risiko dan return dalam investasi, mengelompokkan jenis risiko menjadi risiko tunggal dan risiko portofolio, serta menjelaskan pentingnya diversifikasi untuk mengurangi risiko. Penghitungan return yang diharapkan diilustrasikan melalui contoh perhitungan varians dan standar deviasi, serta cara estimasi risiko portofolio dengan mempertimbangkan kovarians antar sekuritas. Selain itu, dokumen ini juga menekankan pentingnya koefisien variasi sebagai ukuran risiko relatif dalam pengambilan keputusan investasi.

1. Oleh:
Ajeng Putri Naradita(166020202111004)
Olyvia Resyana Citra (166020202111009)
Mohamad Fariz Dwi Permana (166020202111011)
Ni Putu Ayu Dhita Apsari (166020202111016)
RISK & RETURN

2. RISK
RISK (RISIKO)
Kemungkinan terjadinya
hasil yang tidak
diinginkan
Berlawanan dari yang
diinginkan

3. 1. Penyuka / pencari risiko (risk seeker
/ lover / taker)
2. Netral terhadap risiko (risk
neutral)
3. Tdk menyukai / menghindari risiko
(risk averter)

4. RISK
RISK (RISIKO)
On a stand alone basis
(risiko tunggal)
In a portfolio context
(risiko aset dalam suatu
portofolio)

5. Risiko Tunggal (Stand
Alone Risk)
Mengukur risiko tunggal:
• Return yang diharapkan (Expected Return)
• Deviasi standar return
• Koefisien variasi
RISIKO TUNGGAL INVESTOR
MENGADAKAN
SATU ASSET.

6. 1. Risiko dalam konteks aset tunggal.
 Risiko yang harus ditanggung jika
berinvestasi hanya pada satu aset saja.
2. Risiko dalam konteks portofolio
aset.
a. Risiko sistematis (risiko pasar/risiko umum).
 Terkait dengan perubahan yang terjadi di
pasar dan mempengaruhi return seluruh
saham yang ada di pasar.
b. Risiko tidak sistematis (risiko spesifik).
 Terkait dengan perubahan kondisi mikro
perusahaan, dan bisa diminimalkan dengan
melakukan diversifikasi.

7. semua
kemungkinan nilai
& masing2
probabilitas. Semakin
rapat
distribusi
probabilita
s,
Risiko
semakin
kecil

8. Return yang diharapkan (Expected Rate of Return)
E (R) = Return yang diharapkan dari suatu sekuritas
Ri = Return ke-i yang mungkin terjadi
pri = Probabilitas kejadian return ke-i
n = Banyaknya return yang mungkin terjadi
rata2 tertimbang dari distribusi
probabilitas
E(R) =
n
i
ii prR
1

9. Berikut ini akan diberikan contoh perhitungan return yang diharapkan dari
suatu sekuritas ABC berdasarkan skenario kondisi ekonomi seperti dalam Tabel
1 di bawah ini:
Kondisi Ekonomi Probabilitas Return
Ekonomi kuat 0,30 0,20
Ekonomi sedang 0,40 0,15
Resesi 0,30 0,10
Tabel 1
Distribusi Probabilitas Sekuritas ABC

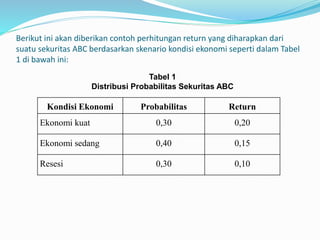
10. Penghitungan return yang diharapkan dari sekuritas ABC tersebut
bisa dihitung dengan rumus di atas, seperti berikut ini :
E (R)= [(0,30) (0,20)] +  (0,4) (0,15)  + (0,30 (0,10)]
= 0,15
Jadi, return yang diharapkan dari sekuritas ABC adalah sebesar 0,15 atau
15%.

11. Menghitung Resiko
Investor harus mampu menghitung risiko dari suatu
investasi.
Untuk menghitung besarnya risiko total yang
dikaitkan dengan return yang diharapkan dari suatu
investasi, bisa kita lakukan dengan menghitung
varians dan standar deviasi return investasi
bersangkutan.

12. Dimana :
 2 = Varians return
  = Standar deviasi
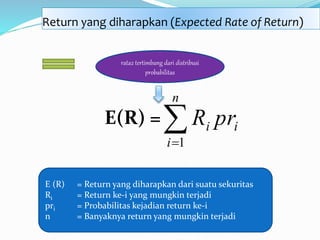
 E (R) = Return yang diharapkan dari suatu sekuritas
 Ri = Return ke-i yang mungkin terjadi
 pri = probabilitas kejadian return ke-i
Varians return = 2 = [RI – E (R)]2pri
Standar deviasi =  = (2)12
Rumus Varians Return :
Rumus Standar Deviasi :

13. Dalam Tabel 2 berikut ini diberikan contoh perhitungan varians dan standar
deviasi saham DEF.
Tabel 2
Penghitungan Varians dan Standar Deviasi Saham DEF
(1)
Return
(Ri)
(2)
Probabilitas
(pri)
(3)
(1) x (2)
(4)
Ri – E (R)
(5)
[(Ri – E(R)]2
(6)
[(ri – E(R)]2 pri
0,07 0,2 0,014 -0,010 0,0001 0,00002
0,01 0,2 0,002 -0,070 0,0049 0,00098
0,08 0,3 0,024 0,000 0,0000 0,00000
0,10 0,1 0,010 0,020 0,0004 0,00004
0,15 0,2 0,030 0,070 0,0049 0,00098
1,0 E (R) =
0,080
Varians =
0,00202
Standar deviasi =  = (2)1/2 = (0,00202)1/2 = 0,0449 = 4,49%

14.  Dalam pengukuran risiko sekuritas kita juga perlu
menghitung risiko relatif sekuritas tersebut. Risiko
relatif ini menunjukkan risiko per unit return yang
diharapkan. Hal ini diperlukan karena informasi risiko
yang hanya berupa varians dan standar deviasi
kadangkala bisa menyesatkan, terutama jika terdapat
penyebaran return diharapkan yang sangat besar.
Ukuran risiko relatif yang bisa dipakai adalah
koefisien variasi.

15. Terdapat dua pilihan investasi, yaitu A dengan return yg diharapkan
lebih tinggi dan B mempunyai deviasi standar lebih rendah.
PROYEK A PROYEK B
Return yang diharapkan 60% 8%
Deviasi standar 15% 3%
Koefisien Variasi
15 = 0.25
60
3 = 0.37
8
0.37 > 0.25 berarti proyek B lebih berisiko daripada
proyek A
Contoh: Apabila terdapat 2 proyek, A&B
Contoh Lain

16. PORTOFOLIO
KOMBINASI
DUAATAU
LEBIH ASSET.
RISIKO ASET
LEBIH KECIL
Risiko Aset dalam Suatu Portofolio (Risk in
Portopolio Context)

17. Analisis Risiko Portofolio
TINGKAT
RESIKO

18. Rumus untuk menghitung varians portofolio
p =
2/1
n
i
Contoh: Misalnya risiko setiap sekuritas sebesar 0,20, maka risiko
portofolio akan menurun terus jika semakin banyak jumlah sekuritas yang
dimasukkan dalam portofolio. Misalnya, jika kita memasukkan 100 saham
dalam portofolio tersebut maka risiko portofolio akan berkurang dari 0,20
menjadi 0,02
02,0
100
20,0
2/1
p

19. PENGARUH PENAMBAHAN JENIS ASET
TERHADAP RESIKO PORTOFOLIO

20. DIVERSIFIKASI
 Untuk menurunkan risiko portofolio, investor perlu
melakukan ‘diversifikasi’, dengan membentuk portofolio
sedemikian rupa hingga risiko dapat diminimalkan tanpa
mengurangi return yang diharapkan.
 Diversifikasi bisa dilakukan dengan:
1. Diversifikasi random.
- Memilih aset yang akan dimasukkan dalam portofolio secara
acak.
2. Diversifikasi model Markowitz.
- Memilih aset yang dimasukkan dalam portofolio berdasar
berbagai informasi dan karakteristik aset.

21. Risiko Portofolio
Koefisien Korelasi Kovarians
Perhitungan Risiko Portofolio
Return yang
Diharapkan

22. Ukuran korelasi biasanya dilambangkan dengan
(i,j) dan berjarak (berkorelasi) antara +1,0
sampai –1,0, dimana:
Korelasi Vs manfaat pengurangan risiko:
 Penggabungan dua sekuritas yang
berkorelasi positif sempurna (+1,0) tidak
akan memberikan manfaat pengurangan
risiko.
 Penggabungan dua sekuritas yang
berkorelasi nol, akan mengurangi risiko
portofolio secara signifikan.

23.  Korelasi Vs manfaat pengurangan risiko :
 Penggabungan dua buah sekuritas yang
berkorelasi negatif sempurna (-1,0) akan
menghilangkan risiko kedua sekuritas
tersebut.
 Dalam dunia nyata, ketiga jenis korelasi
ekstrem tersebut (+1,0; 0,0; dan –1,0) sangat
jarang terjadi. Oleh karena itu, investor tidak
akan bisa menghilangkan sama sekali risiko
portofolio. Hal yang bisa dilakukan adalah
‘mengurangi’ risiko portofolio.

24. KOVARIANS
Kovarians menunjukkan sejauhmana return dari dua
sekuritas mempunyai kecenderungan bergerak
bersama-sama. Kovarians bisa berbentuk angka
positif, negatif ataupun nol.
Secara matematis, rumus untuk menghitung kovarians
dua buah sekuritas A dan B adalah :
CovAB =   iBiBAiA prRERRER )]()][([ ,,

25. ESTIMASI RETURN PORTOFOLIO
 Return yang diharapkan dari suatu portofolio bisa
diestimasi dengan menghitung rata-rata
tertimbang dari return yang diharapkan dari
masing-masing aset individual yang ada dalam
portofolio.
 Rumusnya adalah :


n
1i
)E(RW)E(R iip

26. Estimasi Return Portofolio
 Sebuah portofolio yang terdiri dari 3 jenis saham
ABC, DEF dan GHI menawarkan return yang
diharapkan masing-masing sebesar 15%, 20%
dan 25%.
 Misalnya, prosentase dana yang diinvestasikan
pada saham ABC sebesar 40%, saham DEF
30% dan saham GHI 30%.
 Maka, return yang diharapkan:
E(Rp) = 0,4 (0,15) + 0,3 (0,2) + 0,3 (0,25)
= 0,195 atau 19,5%

27. Estimasi Risiko Portofolio
Dalam menghitung risiko portofolio, ada tiga
hal yang perlu ditentukan, yaitu :
1. Varians setiap sekuritas
2. Kovarians antara satu sekuritas dengan
sekuritas lainnya.
3. Bobot portofolio untuk masing-masing
sekuritas.

28. Terima Kasih