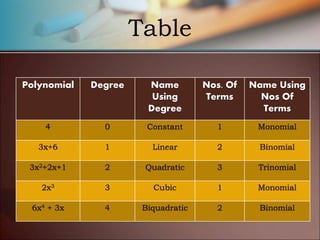
This document provides an overview of polynomials, including: - Defining polynomials as expressions involving variables and coefficients using addition, subtraction, multiplication, and exponents. - Discussing the history of polynomial notation pioneered by Descartes. - Explaining the different types of polynomials like monomials, binomials, and trinomials. - Outlining common uses of polynomials in mathematics, science, and other fields. - Describing how to find the degree of a polynomial and graph polynomial functions. 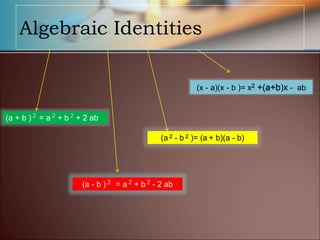- Explaining arithmetic operations like addition, subtraction, and division that can be performed on polynomials.

2. Table Of Contents -
• Introduction
• History
1. History Of Notation
• Terms
• Types Of Polynomials
• Uses
• Zeroes Of Polynomial
• Degree
• Graphs Of Polynomial Function
• Table
• Algebraic Identities
• Arithmetic Of Polynomials
• Think Tanker ? ?

3. Introduction…..
~ What Is a Polynomial ??
In mathematics, a polynomial is an expression
consisting of variables and coefficients, that
involves only the operations of addition,
subtraction, multiplication, and non-negative
integer-exponents.
Example : x2 − 3x + 6, which is a quadratic
polynomial.

4. History Of Notation
• He popularized the use of letters from the
beginning of the alphabet to denote constants and
letters from the end of the alphabet to denote
variables.
• As can be seen above, in the general formula for a
polynomial in one variable, where the a's denote
constants and x denotes a variable.
• Descartes introduced the use of superscripts to
denote exponents as well.

5. NEXT

6. Types Of Polynomials...
Monomial
In mathematics,
A monomial is a
polynomial with
just one term.
For Example:
3x,4xy is a
monomial.
Binomial
In algebra, A
binomial is a
polynomial, which
is the sum of two
monomials.
For Example:
2x+5 is a
Binomial.
Trinomial
In elementary
algebra, A
trinomial is a
polynomial
consisting of three
terms or
monomials.
For Example :
3x+5y+7z is a
Trinomial.

7. Binomial TrinomialMonomial

8. Uses...
• Polynomials appear in a wide variety of areas of
mathematics and science.
~ For example, they are used to form “Polynomial”
equations, which encode a wide range of problems, from
elementary word problems to complicated problems in the
sciences.
• They are used to define “Polynomial Functions”, which
appear in settings ranging from basic chemistry and
physics to economics and social science.
• They are used in calculus and numerical analysis to
approximate other functions.

9. Zeroes Of Polynomial
• Consider the polynomial p(x) = 5x3 – 2x3+ 3x – 2.
If we replace x by 1 everywhere in p(x), we get
p(1) = 5 × (1)3 – 2 × (1)2 + 3 × (1) – 2
= 5 – 2 + 3 –2
= 4
So, we say that the value of p(x) at x = 1 is 4.
Similarly,
p(0) = 5(0)3 – 2(0)2 + 3(0) –2
= –2

10. Degree
• The degree of a polynomial is the highest
degree of its terms, when the polynomial is
expressed in canonical form (i.e., as a linear
combination of monomials). The degree of a
term is the sum of the exponents of the
variables that appear in it.

11. DEGREE OF POLYNOMIAL
• Degree 0 – constant
• Degree 1 – linear
• Degree 2 – quadratic
• Degree 3 – cubic
• Degree 4 – quartic (or, less
commonly, biquadratic)

13. Look at each term,
whoever has the most letters wins!
x2 – 4x4 + x6
This is a 8th degree polynomial:
xy4 + x4y4 + 12
This guy has 6 letters…
The degree is 6.
This guy has 8 letters…
The degree is 8
Here’s how you find the degree
of a polynomial :

14. The graph of the zero polynomial
f(x) = 0 is the x-axis.
Graphs Of Polynomial
Functions ..

15. The graph of the polynomial of degree 2
Graphs Of Polynomial
Functions ..

16. Table
Polynomial Degree Name
Using
Degree
Nos. Of
Terms
Name Using
Nos Of
Terms
4 0 Constant 1 Monomial
3x+6 1 Linear 2 Binomial
3x2+2x+1 2 Quadratic 3 Trinomial
2x3 3 Cubic 1 Monomial
6x4 + 3x 4 Biquadratic 2 Binomial

17. Algebraic Identities
(a + b ) 2 = a 2 + b 2 + 2 ab
(a - b ) 2 = a 2 + b 2 - 2 ab
(a 2 - b 2 )= (a + b)(a - b)
(x - a)(x - b )= x2 +(a+b)x - ab

18. Arithmetic Of Polynomials
• Addition ( + )
• Subtraction( - )
• Division ( / )

19. Addition Of Polynomials…..
• Polynomials can be added using the associative law of
addition (grouping all their terms together into a single
sum), possibly followed by reordering, and combining of
like terms. For example, if
Method 1: Line up like terms. Then add the coefficients.
P = 3x + 7
Q = 2x + 3
P + Q = 5x + 10

20. Addition Of Polynomials…..
Method 2 :
Group like terms. Then add the coefficients.
4x2 + 6x + 7 + 2x2 – 9x + 1 = (4x2 + 2x2)+(6x – 9x)+ (7+1)
= 6x2 – 3x + 8
» The sum of two polynomials is also a polynomial.

21. Subtraction Of Polynomials
• Earlier you learned that subtraction means to add
the opposite. So when you subtract a polynomial,
change the signs of each of the terms to its opposite.
Then add the coefficients.
Method 1:
Line up like terms. Change the signs of the second
polynomial, then add. For Example:
4x - 7 4x - 7
-(2x + 3)  -2x – 3
2x - 10

22. Subtraction Of Polynomials
Method 2:
Simplify: (5x2 – 3x) – (-8x2 + 11)
Write the opposite of each term :
5x2 – 3x + 8x2 – 11
Group like terms :
(5x2 + 8x2) + (3x + 0) + (-11 + 0) = 13x2 + 3x – 11
»The difference of two polynomials is also a polynomial

23. Division Of Polynomials
• The Methods Used For Finding Divison Of
Polynomials Are:
1. Long Division Method
2. Factor Theorem

24. Long- Division Method
• In arithmetic, long division is a standard division
algorithm suitable for dividing multi-digit numbers
that is simple enough to perform by hand.
• It breaks down a division problem into a series of
easier steps.
• As in all division problems, one number, called the
dividend, is divided by another, called the divisor,
producing a result called the quotient.
Dividend = (Divisor × Quotient) + Remainder

25. Long- Division Method
Dividend = (Divisor × Quotient) + Remainder

26. Factorisation
• Factor Theorem : If p(x) is a polynomial of
degree n > 1 and a is any real number,
Then :
(i) x – a is a factor of p(x), if p(a) = 0,
and
(ii) p(a) = 0, if x – a is a factor of p(x).

28. Q.1 What is the simplified form of :
2x-3x+2??
A. -x+2
B. -5x+2
C. -10x+2
D. -2x+2

29. Q.2 What is the value of x when x+3=10 ??
A. 7
B. 4
C. 2
D. 9

30. Q 3. Solve 2x+4=108 ??
A. 32
B. 56
C. 52
D. 23