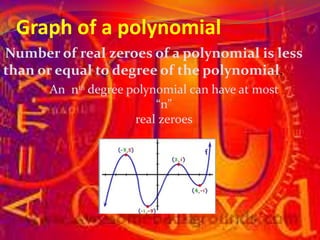
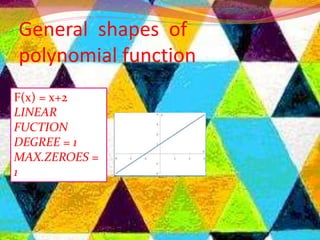
i. The document discusses polynomials, including definitions, types of polynomials based on degree, and key concepts like factorization, the relationship between zeros and coefficients of quadratic and cubic polynomials, and graphs of polynomials. ii. Key results covered are: (x3+y3) = (x+y)(x2-xy+y2), the remainder theorem, and the factor theorem. iii. Examples of polynomial factorization and the relationship between zeros and coefficients are provided.

2. DSBM SR. SEC. SCHOOL ALIGARH
Priyansh upadhyay (9th A) Roll no.39

3. Acknowledgement
 To our Listener whom we owe all our hard work
and dedication. The main motive behind this
presentation is to convey some facts and data
related to polynomial.
 Special thanks :- To my parents , teachers and
school staff who provided all the materials and
valuable advise which helped me to make the
presentation more attractive

4. Contents
 Introduction
 Polynomials
 Types of polynomial
 Polynomial of various degree
 Remainder theorem
 Factor theorem
 Factorization and methods of factorization
 The relationship between the zeroes and coefficients of quadratic
polynomial and cubic
 Graphs of a polynomial and general shapes of a polynomial

5. Introduction
Polynomial are algebraic expression that
include real number and variables . The
power of variables should always be a
whole number . Division and square roots
cannot be involved in the variable . The
variable can only include addition ,
subtraction and multiplication.

6. Polynomials
 An algebraic expression in which the variables
involved have only non-negative integral power is
called polynomials
 Example (i) 5x³-4x²+6x-3 is a polynomial in one
variable x
 A polynomial cannot have infinite number of terms.
 Constants : A symbol having a fixed numerical value is
called a constant
Example:- 8,-6,5/7,π,etc. are all constants

7. Important points about Polynomials
 A polynomial can have many terms but not infinite terms.
 Exponent of a variable of a polynomial cannot be negative.
This means, a variable with power - 2, -3, -4, etc. is not allowed.
If power of a variable in an algebraic expression is negative,
then that cannot be considered a polynomial.
 The exponent of a variable of a polynomial must be a whole
number.
 Exponent of a variable of a polynomial cannot be fraction. This
means, a variable with power 1/2, 3/2, etc. is not allowed. If
power of a variable in an algebraic expression is in fraction,
then that cannot be considered a polynomial.
 Polynomial with only constant term is called constant
polynomial.
 The degree of a non-zero constant polynomial is zero.
 Degree of a zero polynomial is not defined.

9. Polynomial vocabulary
In the polynomial 7x⁵+x²y²-4xy+7
there are 4 terms 7x⁵,x²y²,-4xy
and 7
the coefficient of term 7x⁵is 7
of term x²y²is 1
of term -4xy is -4
and
of term 7 is 7.
7 is a constant term.

10. Evaluating polynomial
 Evaluating polynomial for a polynomial value involves
replacing the value for the variable(s) involved.
Example :-
Find the value of 2x³-3x+4 when x=-2.
2x³-3x+4 = 2(-2)³-3(-2)+4
= 2(-8)+6+4
= -16+10
= -6

11. Combining like terms
 Like terms are terms that contain exactly the same variables
raised to exactly the same powers.
Warning!
Only like term can be combined through addition and
subtraction.
Example
Combine like terms to simplify.
x²y+xy-y+10x²y-2y+xy
= x²y+10x²y+xy+xy-y-2y (like terms are grouped together)
= (1+10)x²y+(1+1)xy+(-1-2)y = 11x²y+2xy-3y

12. Polynomial contains three types of
term;
(1) Monomial : A polynomial containing one
nonzero term is called a monomial
Example: 5, 3x, 1/3xy are all monomials.
(2) Binomial : A polynomial containing two
nonzero term is called binomial.
Example:(3+6x),(x-5y)
(3) Trinomial : A polynomial containing three
nonzero terms is called trinomial
Example : (8+3x+x³), (xy+yz+zx)

13. Polynomial of various degree
(i)Linear polynomial : A polynomial of degree one is called
a linear polynomial .
Example :- 3x+5 is a linear polynomial in x.
(ii)Quadratic polynomial : A polynomial of degree two is
called a quadratic polynomial.
Example :- x²+5x-1/2 is a quadratic polynomial in x .
(iii)Cubic polynomial : A polynomial of degree three is
called cubic polynomial
Example:- 4x³-3x²+7x+1 is a cubic polynomial.
(iv) Biquadratic polynomial:- A polynomial of degree four
is called biquadratic polynomial.
Example:- x²y²+xy³+y⁴-8xy+y²+7 is a biquadratic
polynomial in x and y.

14. Remainder theorem
 Let f(x) be a polynomial of degree n˃1 and let a be any
real number.
When f(x) is divided by (x-a),then the remainder is f(a).
PROOF: Suppose that when f(x) is divided by (x-a),the
quotient is g(x) and the remainder is (x).
Then,degree r( x)<degree(x-a)
Degree r(x)<1
Degree r(x)=0
r(x) is constant , equal to r(say)
Thus,when f(x)is divided by (x-a),then the quotient is g(x)
and the remainder is r. …f(x)=(x-a).g(x)+r
Putting x=a in (i), we get r=f(a).
Thus, when f(x) is divided by (x-a), then the remainder is
f(a).

15. Factor theorem Let f(x) be a polynomial of degree n>1 and let a be any real number
(i) if (a) =0 then (x-a) is a factor of f(x).
(ii) if (x-a) is a factor of f(x) then f(a) =0.
PROOF: (i) Let f(a) =0
On dividing f(x) by (x-a), let g(x) be the quotient .
Also, by the remainder theorem,when f (x)is divided by (x-a),then the remainder
is f(a).
f(a)=(x-a).g(x)+f(a)
=> f(x)=(x-a).g(x).
 (x-a) is a factor of f(x).
(ii) Let (x-a) be a factor of f(x).
On dividing f(x) by (x-a), let g(x) be the quotient.
Then , f(a)=(x-a).g(x)
 f(a) = 0
 Thus ,(x-a) is a factor of f(x)
 F(a) =a.

16. Factorization To express a given polynomial as the product of
polynomial , each of degree less than that of the given
polynomial such that no such a factor has a factor of
lower degree, is called factorization
Formulae for factorization
(i) (x+y)² = x²+y²+2xy
(ii) (x-y)² = x²+y²-2xy
(iii) (x+y+z)² = x²+y²+z²+2xy+2yz+2zx
(iv)(x+y)³ = x³+y³+3xy(x+y)
(v) (x-y)³ = x³-y³-3xy(x-y)
(vi) (x²-y²) = (x-y)(x+y)
(vii) (x³+y³) = (x+y)(x²-xy+y²)
(viii) (x³-y³) = (x-y)(x²+xy+y²)

17. Method of factorization
 Factorization by taking out the common factor
Method :- when each term of an expression has a common
factor, we divide each term by this factor and take it out
as a multiple
Example :- 5x²-20xy = 5x(x-4y).
 Factorization by grouping
Method:- Sometimes in a given expression it is not possible
to take out a common factor directly . However, the term
of the given expression are grouped in such a manner that
we may have a common factor.
Example:- ab+bc+ax+cx =(ab+bc)+(ax+cx)
=b(a+c)+x(a+c)= (a+c)(b+x)

18. Factorization of Quadratic
trinomials
 Polynomial of the form x²+bx+c
we find integers p and q such that p+q=b and pq=c.
then,
x²+bx+c = x²+(p+q)x+pq
= x²+px+qx+pq
=x(x+p)+q(x+p) = (x+p)(x+q).
Square of trinomial
(x+y+z)² = x²+y²+z²+2xy+2yz+2zx.
Cube of binomial
(i) (x+y)³=x³+y³+3xy(x+y).
(ii) (x-y)³ = x³-y³-3xy(x-y).

19. Relation between the zeroes and
coefficient of a quadratic polynomial
• A+B = -Coefficient of -b
• Ab = constant term = c
________________________
Coefficient of x² = __
a
________________________
Coefficient of x²
Note :- ‘a’ and ‘b’
are the zeroes

20. Graph of a polynomial
Number of real zeroes of a polynomial is less
than or equal to degree of the polynomial.
An nᵗʱ degree polynomial can have at most
“n”
real zeroes

21. General shapes of
polynomial function
F(x) = x+2
LINEAR
FUCTION
DEGREE = 1
MAX.ZEROES =
1

23. Division algorithm for
polynomial
If p(x) and g(x) are any two polynomials with
g(x) ≠ 0 , then we can always find polynomials
q(x), and r(x) such that :-
P(x) = q(x)g(x)+r(x)
Where r(x) = 0 or degree r(x) < degree g(x)

24.  Theorem 1 :- Prove that
(x³+y³+z³-3xyz) = (x+y+z)(x²+y²+z²-xy+yz+zx).
proof :- we have
(x³+y³+z³-3xyz) = (x³+y³)+z³-3xyz
= [(x+y)³-3xy(x+y)]+z³-3xyz
= u³-3xyu+z³-3xyz, where (x+y) = u
=(u³+z³)-3xy(u+z)
= (u+z)(u²+z²-uz-3xy)
= (x+y+z)[(x+y)²+z²-(x+y)z-3xy]
= (x+y+z)(x²+y²+z²-xy-yz-zx).
: (x³+y³+z³-3xyz) = (x+y+z)(x²+y²+z²-xy-yz-zx).

25.  Theorem 2 :- if (x+y+z) = 0,
prove that (x³+y³+z³) = 3xyz.
Proof ; we have
x+y+z = 0 => x+y = -z
=> (x+y)³ = (-z)³
=> x³+y³+3xy(x+y) = -z³
=> x³+y³+3xy(-z) = -z³ [ : (x+y) = -z ]
=> x³+y³-3xyz = -z³
=> x³+y³+z³ = 3xyz.
Hence, (x+y+z) = 0 => (x³+y³+z³) = 3xyz.

26. Summary
 i. (x³+y³) = (x+y)(x²-xy+y²)
 ii. (x³-y³) = (x-y)(x²+xy+y²)
 iii.(x³+y³+z³-3xyz)= (x+y+z)(x²+y²+z²-xy-yz-zx)
 iv. (x+y+z) = 0 => (x³+y³+z³) = 3xyz
 Remainder theorem:- let p(x) be a polynomial of
degree n>1 and let a be any non-zero real number .
When p(x) is divided by (x-a), then the remainder is
p(a).
 Factor theorem:- let p(x) be a polynomial of degree
n>1 and let a be any real number.
(i) if f(a) = 01, then (x-a) is a factor of f(x).
(ii) if (x-a) is a factor of f(x), then f(a) = 0.

27. MCQ Question
1 :- If x² +ax +b is divided by x + c, then remainder is
(A) :- c ² - ac – b (B) :- c ² - ac + b
(C) :- c ² + ac + b (D) :- −c² - ac + b
 2 :- The degree of polynomial p(x) = x+√x²/1 is
(A) :- 0 (B) :- 2
© :- 1 (D) :- 3
 3 :- if one of the factor of x²+x-20 is (x-5). Find the other
(A) :- x-4 (B) x-2
(B) :- x+4 (D) x-5

28. (4) hen 9x² - 6x + 2 is divided by x -3, remainder will be
(A) 60 (B) 15⁄2
(C) 19⁄5 (D) 65
(5) If a specific number x = a is substituted for variable x
in a polynomial, so that value is zero, then x = a is said
to be
(A) zero of the polynomial (B) zero coefficient
(C) conjugate surd (D) rational number