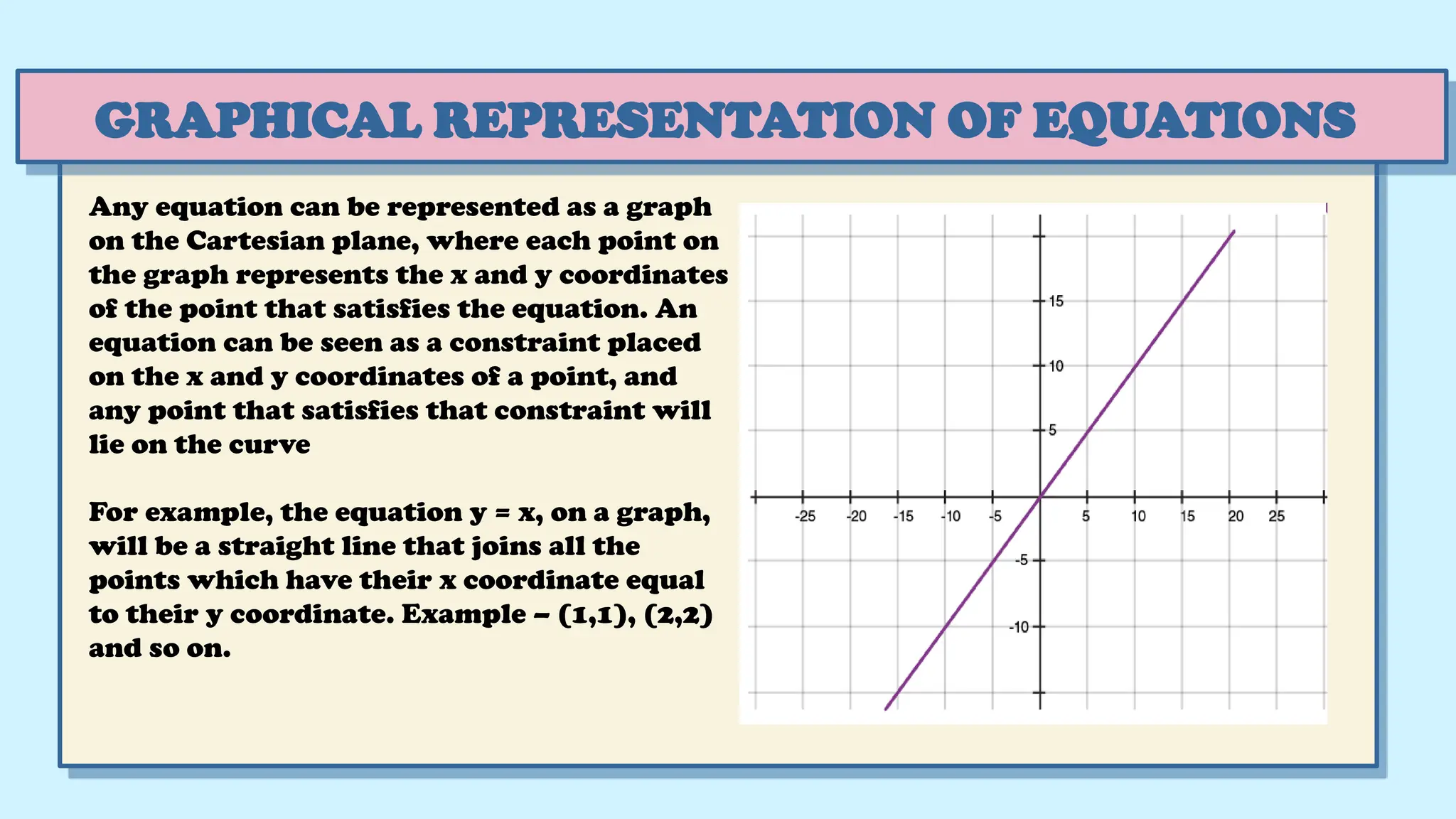
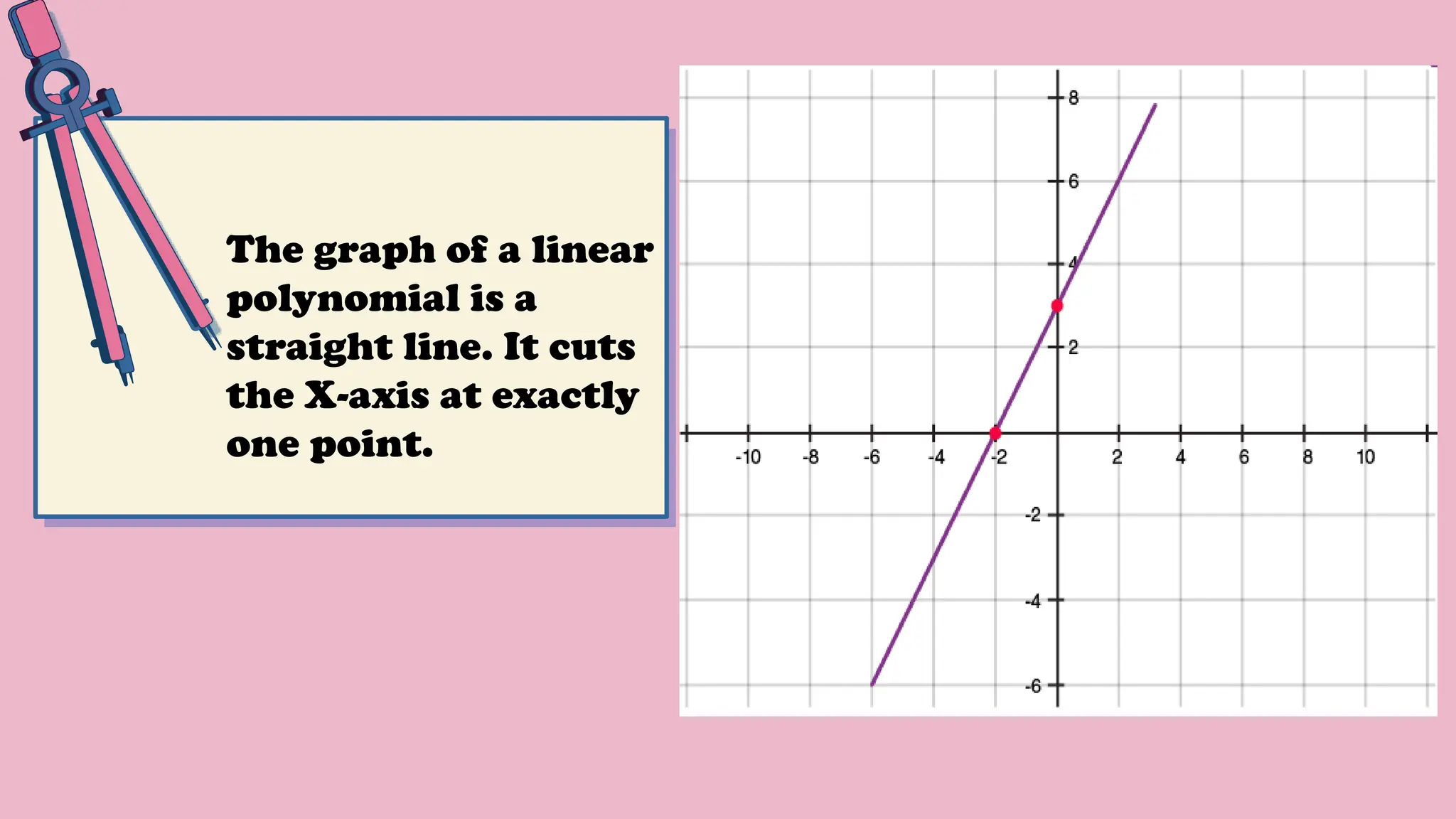
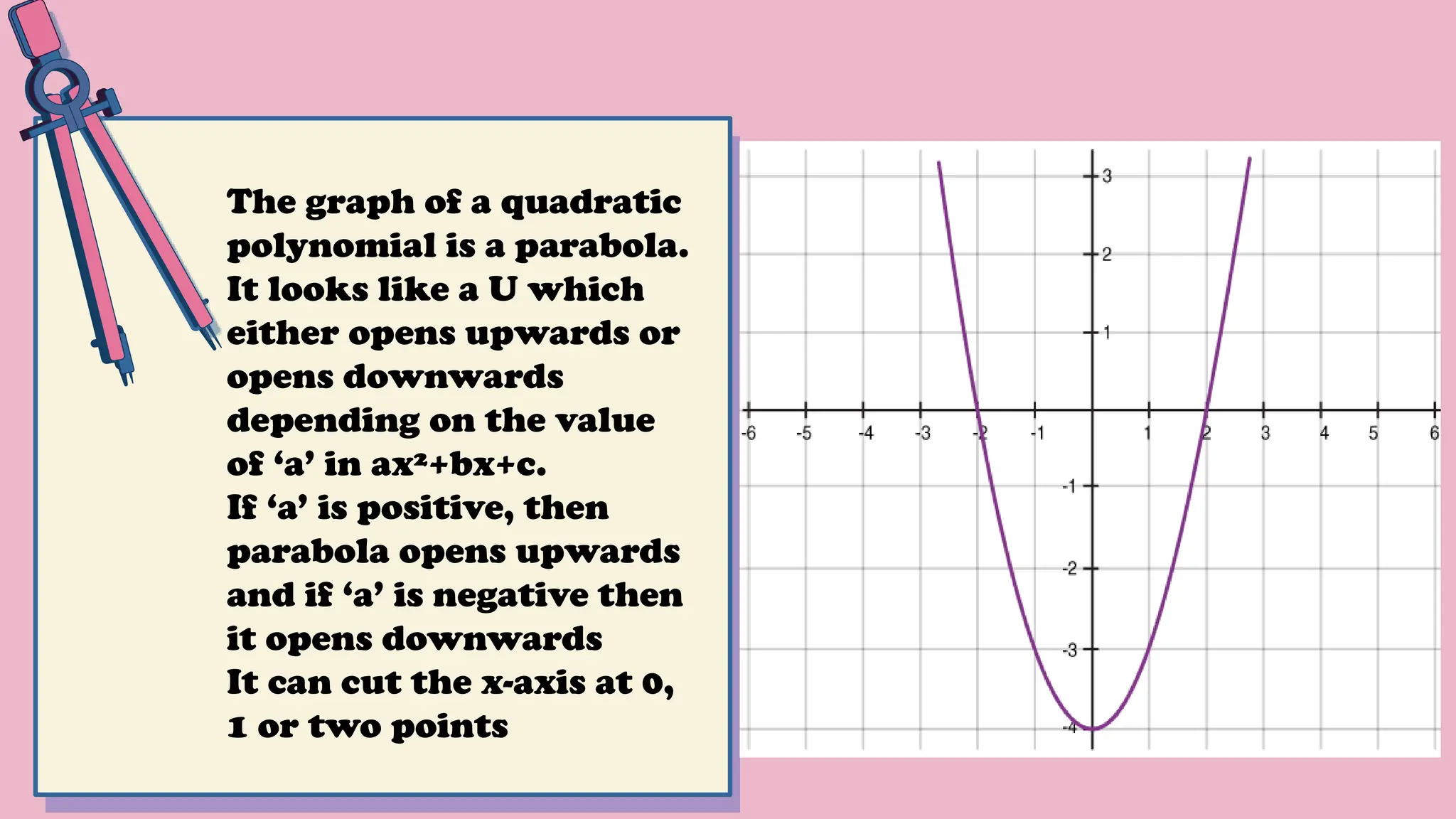
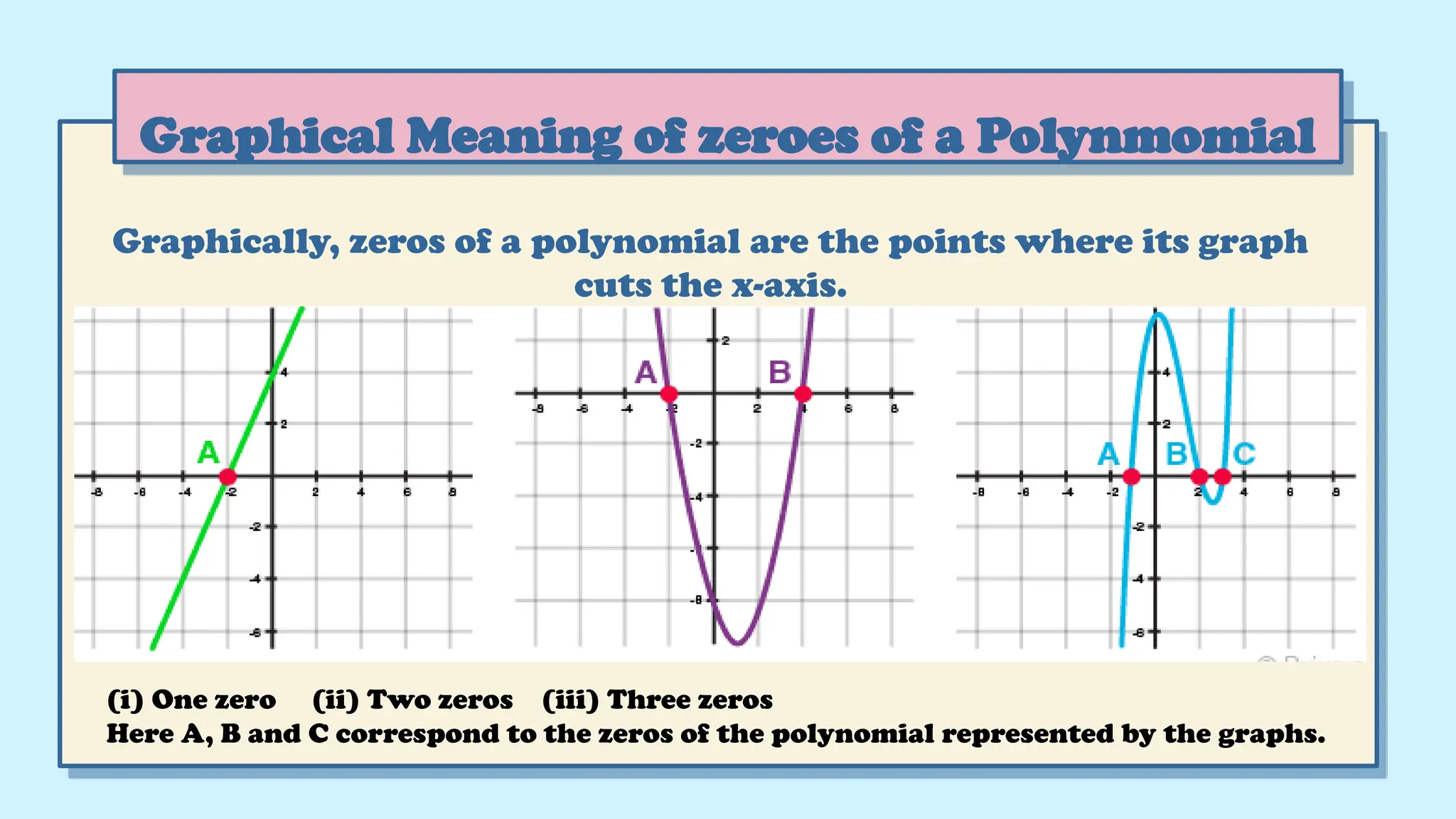
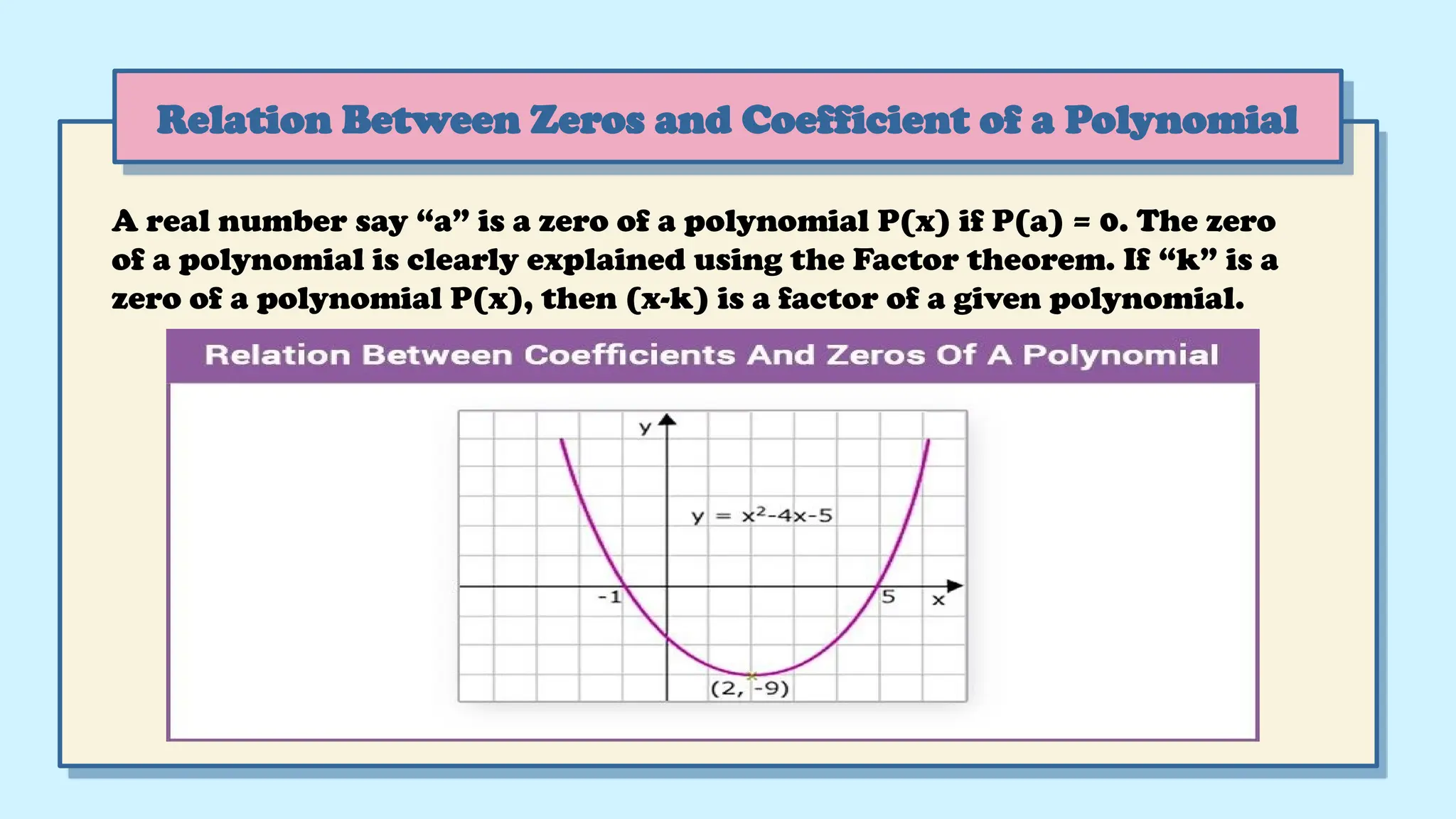
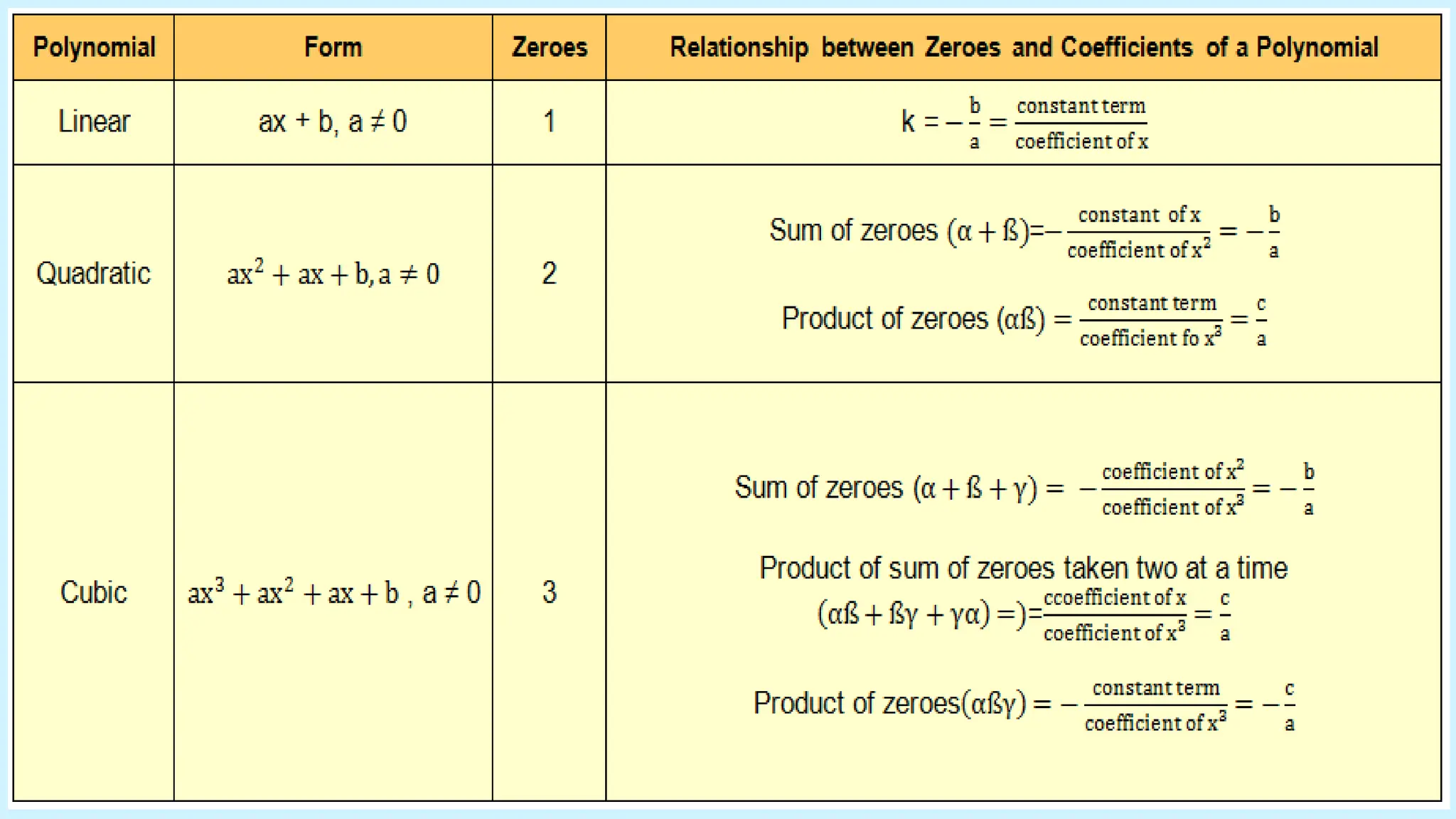
The document provides a comprehensive overview of polynomials, including definitions, classifications, and graphical representations. It covers topics such as the degrees of polynomials, types of polynomials (monomial, binomial, trinomial), and methods for finding zeroes and factorization. Additionally, it explains the relationship between zeroes and coefficients, along with step-by-step instructions for polynomial division.

1. Class - 10th
Polynomials
Prime Paathshala
+91-8989815785

2. Table of contents
 Introduction to polynomials
 Polynomial classifications
 Degrees of a polynomial
 Terms of a polynomial
 Types of polynomials
 Graphical representation of equations
 Zeroes of a polynomial
 Graphical meaning of zeroes of polynomial
 Number of zeroes
 Factorization of polynomials
 Relations between zeroes and coefficient of a
polynomial
 Zeroes of a polynomial examples
 Division algorithm
 Algebraic identities

3. Introduction to Polynomials
The word polynomial is derived from the Greek words ‘poly’ means ‘many‘
and ‘nominal’ means ‘terms‘, so altogether it said “many terms”. A polynomial
can have any number of terms but not infinite. It is defined as an expression
which is composed of variables, constants and exponents, that are combined
using the mathematical operations such as addition, subtraction, multiplication
and division.
Polynomials are algebraic expressions that consist of variables and coefficients.
Variables are also sometimes called indeterminates. For example: x²+x-12.

4. Based on the numbers of terms present in the
expression, it is classified as monomial, binomial, and
trinomial. Examples of constants, variables and
exponents are as follows
Constants. Example: 1, 2, 3, etc.
Variables. Example: g, h, x, y, etc.
Exponents: Example: 5 in x5 etc.
Polynomial Classifications
The polynomial function is denoted by P(x) where x represents the
variable. For example, P(x) = x²+5x+11
If the variable is denoted by a, then the function will be P(a)

5. Degree of a polynomial
The degree of a polynomial is defined as the highest degree of a monomial
within a polynomial. Thus, a polynomial equation having one variable which
has the largest exponent is called a degree of the polynomial.
Example: Find the degree of the
polynomial 6s4+ 3x2+ 5x +19
Solution: The degree of the
polynomial is 4.

6. TERMS OF POLYNOMIAL
The terms of polynomials are the parts of the
equation which are generally separated by “+”
or “-” signs. So, each part of a polynomial in
an equation is a term. For example, in a
polynomial, say, 2x2 + 5 +4, the number of
terms will be 3. The classification of a
polynomial is done based on the number of
terms in it.

7. Polynomials are of 3 different types and are classified
based on the number of terms in it. The three types of
polynomials are:
Monomial
Binomial
Trinomial
TYPES OF POLYNOMIALS
These polynomials can be combined using addition, subtraction,
multiplication, and division but is never division by a variable. A
few examples of Non Polynomials are: 1/x+2, x-3

8. TYPES OF POLYNOMIALS

9. GRAPHICAL REPRESENTATION OF EQUATIONS
Any equation can be represented as a graph
on the Cartesian plane, where each point on
the graph represents the x and y coordinates
of the point that satisfies the equation. An
equation can be seen as a constraint placed
on the x and y coordinates of a point, and
any point that satisfies that constraint will
lie on the curve
For example, the equation y = x, on a graph,
will be a straight line that joins all the
points which have their x coordinate equal
to their y coordinate. Example – (1,1), (2,2)
and so on.

10. The graph of a linear
polynomial is a
straight line. It cuts
the X-axis at exactly
one point.

11. The graph of a quadratic
polynomial is a parabola.
It looks like a U which
either opens upwards or
opens downwards
depending on the value
of ‘a’ in ax²+bx+c.
If ‘a’ is positive, then
parabola opens upwards
and if ‘a’ is negative then
it opens downwards
It can cut the x-axis at 0,
1 or two points

12. ZEROES OF A POLYNOMIAL
A zero of a polynomial p(x) is the value of x for which the
value of p(x) is 0. If k is a zero of p(x), then p(k)=0.
For example, consider a polynomial p(x)=x2 3x+2.
−
When x=1, the value of p(x) will be equal to
p(1)=12 3×1+2
−
=1 3+2
−
=0
Since p(x)=0 at x=1, we say that 1 is a zero of the polynomial
x2 3x+2
−

13. Graphical Meaning of zeroes of a Polynmomial
Graphically, zeros of a polynomial are the points where its graph
cuts the x-axis.
(i) One zero (ii) Two zeros (iii) Three zeros
Here A, B and C correspond to the zeros of the polynomial represented by the graphs.

14. In general, a polynomial of degree n has
at most n zeros.
A linear polynomial has one zero,
A quadratic polynomial has at most two
zeros.
A cubic polynomial has at most 3 zeros.
Number of zeroes

15. Factorization of Polynomials
Quadratic polynomials can be factorized by splitting the middle term.
For example, consider the polynomial 2x² 5x+3
−
Splitting the middle term : The middle term in the polynomial 2x² 5x+3 is -5x. This
−
must be expressed as a sum of two terms such that the product of their coefficients
is equal to the product of 2 and 3 (coefficient of x² and the constant term)
−5 can be expressed as ( 2)+( 3), as 2× 3=6=2×3
− − − −
2x² 5x+3
− = 2x² 2x 3x+3
− −
Now, identify the common factors in individual groups
2x² 2x 3x+3=2x(x 1) 3(x 1)
− − − − −
Taking (x 1) as the common factor, this can be expressed as:
−
2x(x 1) 3(x 1)=
− − − (x 1)(2x 3)
− −

16. Relation Between Zeros and Coefficient of a Polynomial
A real number say “a” is a zero of a polynomial P(x) if P(a) = 0. The zero
of a polynomial is clearly explained using the Factor theorem. If “k” is a
zero of a polynomial P(x), then (x-k) is a factor of a given polynomial.

17. The linear polynomial is an expression, in which the degree of the polynomial is
1. The linear polynomial should be in the form of ax+b. Here, “x” is a variable,
“a” and “b” are constant.
The Quadratic polynomial is defined as a polynomial with the highest degree
of 2. The quadratic polynomial should be in the form of ax2
+ bx + c. In this
case, a ≠ 0.
The cubic polynomial is a polynomial with the highest degree of 3.
The cubic polynomial should be in the form of
ax3
+ bx2
+ cx + d, where a ≠ 0. Let say , , and are the three zeros
α β γ
of a polynomial, then
Zeroes ( , , ) follow the rules of algebraic
α β γ
identities, i.e.,
( + )² = ² + ² + 2
α β α β αβ
∴( ² + ²) = ( + )² – 2
α β α β αβ

19. Zeros of a Polynomial Solved Examples

20. Division Algorithm
To divide one polynomial by another, follow the steps given below.
Step 1: arrange the terms of the dividend and the divisor in the decreasing order of
their degrees.
Step 2: To obtain the first term of the quotient, divide the highest degree term of the
dividend by the highest degree term of the divisor Then carry out the division process.
Step 3: The remainder from the previous division becomes the dividend for the next
step. Repeat this process until the degree of the remainder is less than the degree of the
divisor.
If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then
p(x) = g(x) × q(x) + r(x)
Dividend = Divisor x Quotient + Remainder
If r (x) = 0, then g (x) is a factor of p (x).
If r (x) ≠ 0, then we can subtract r (x) from p (x) and then the new polynomial formed
is a factor of g(x) and q(x).

21. Algebraic Identities

22. CREDITS: This presentation template was created by Slidesgo
, including icons by Flaticon and infographics & images by
Freepik
Thank You!!