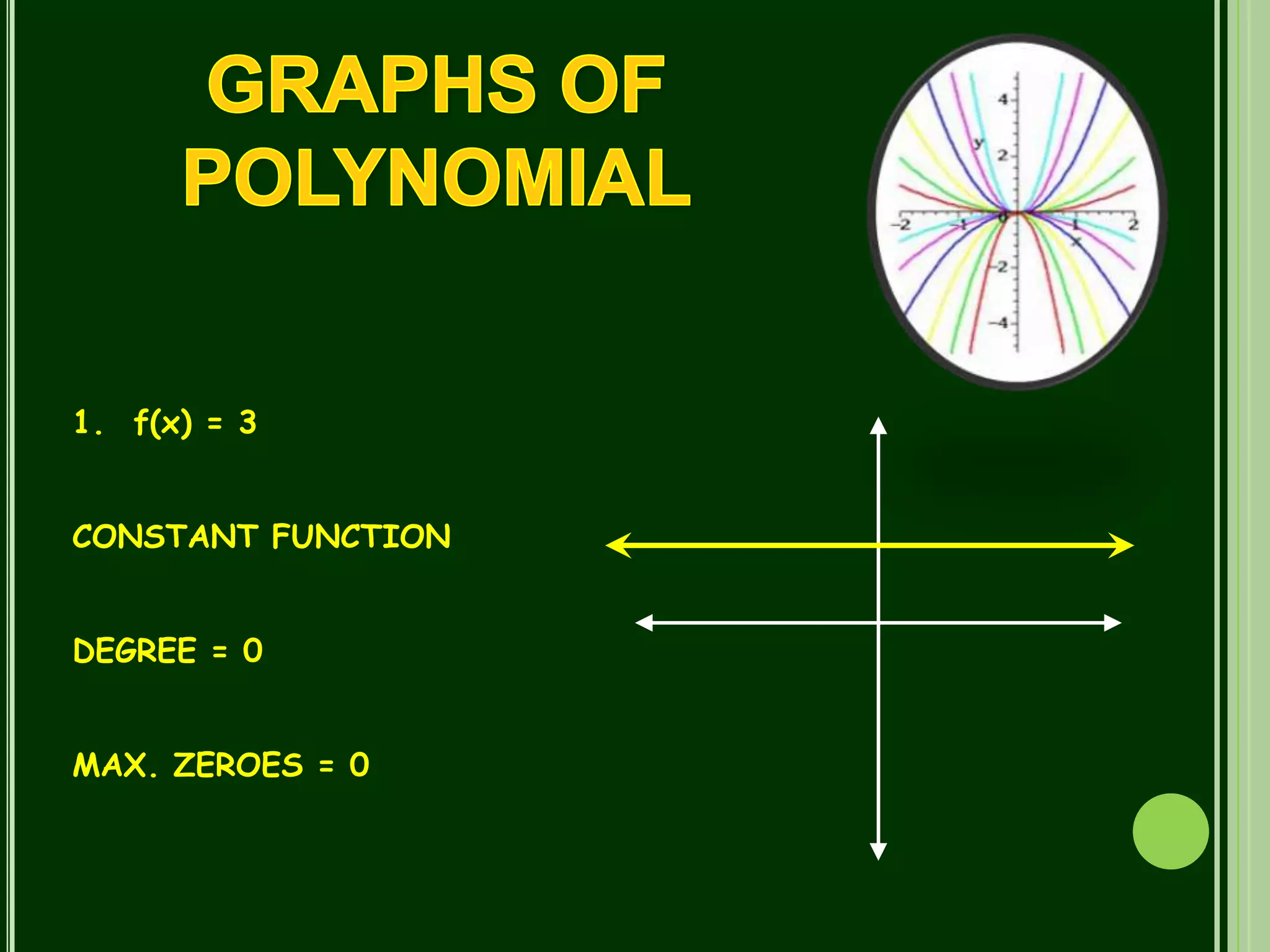
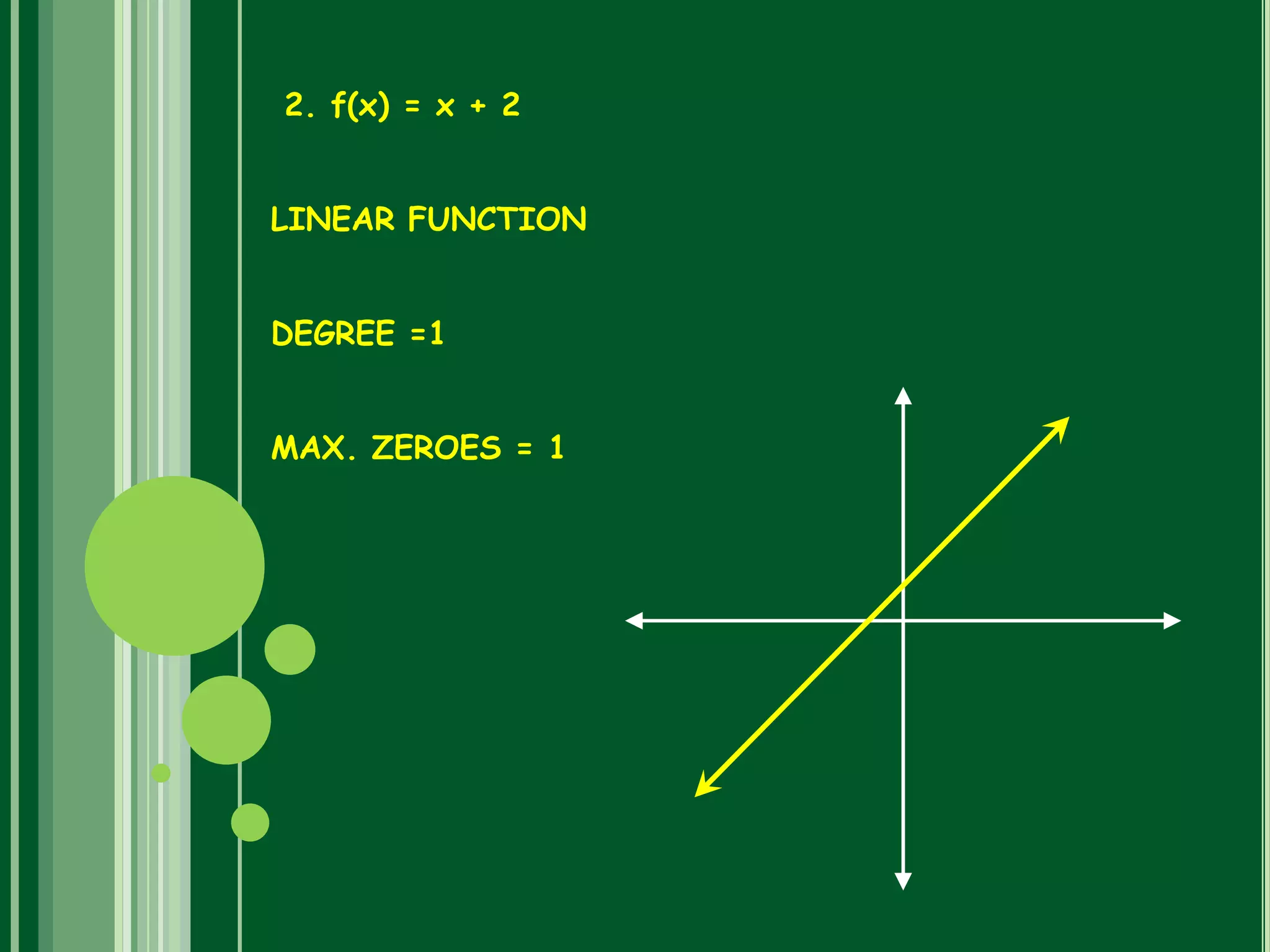
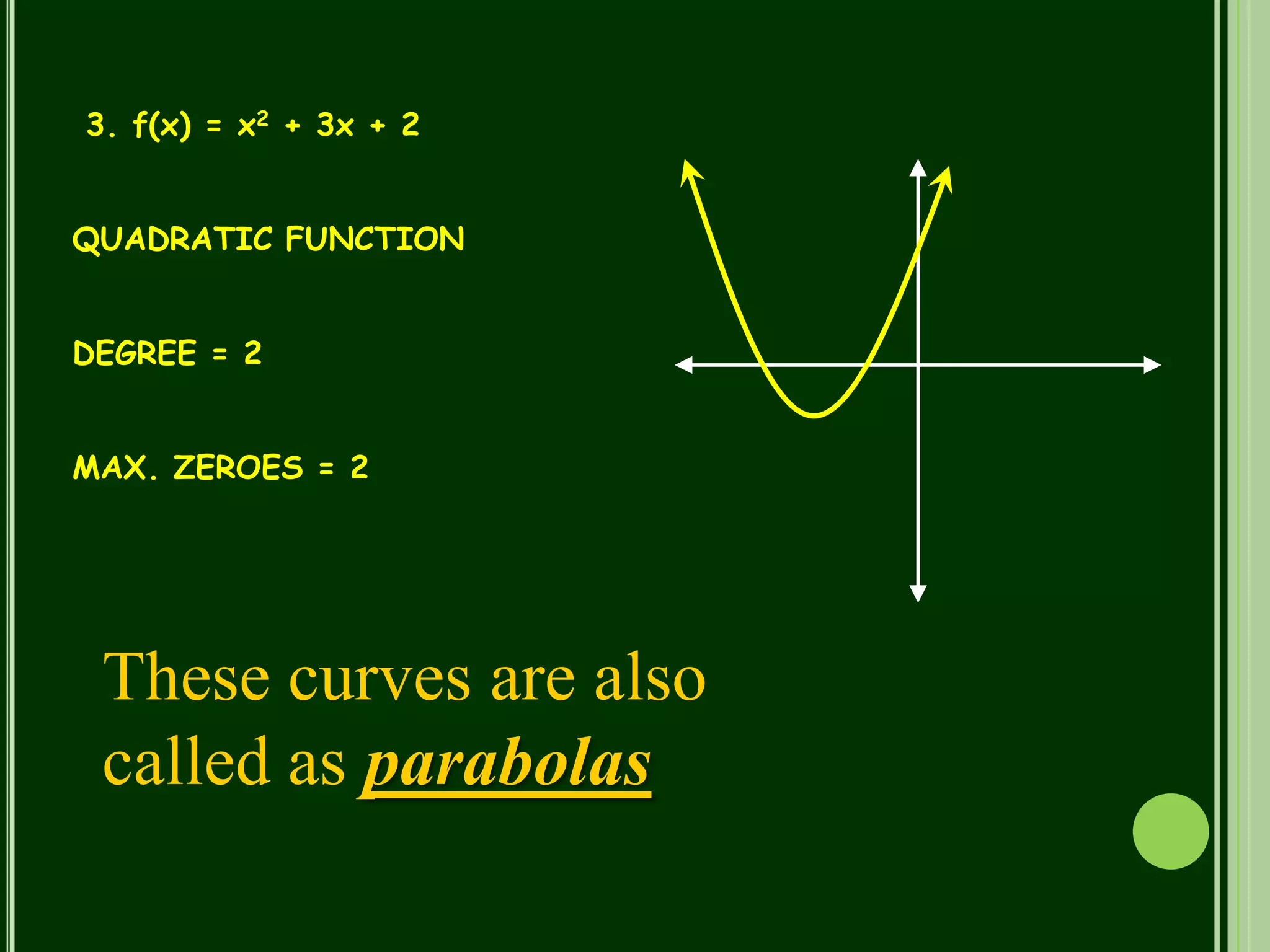
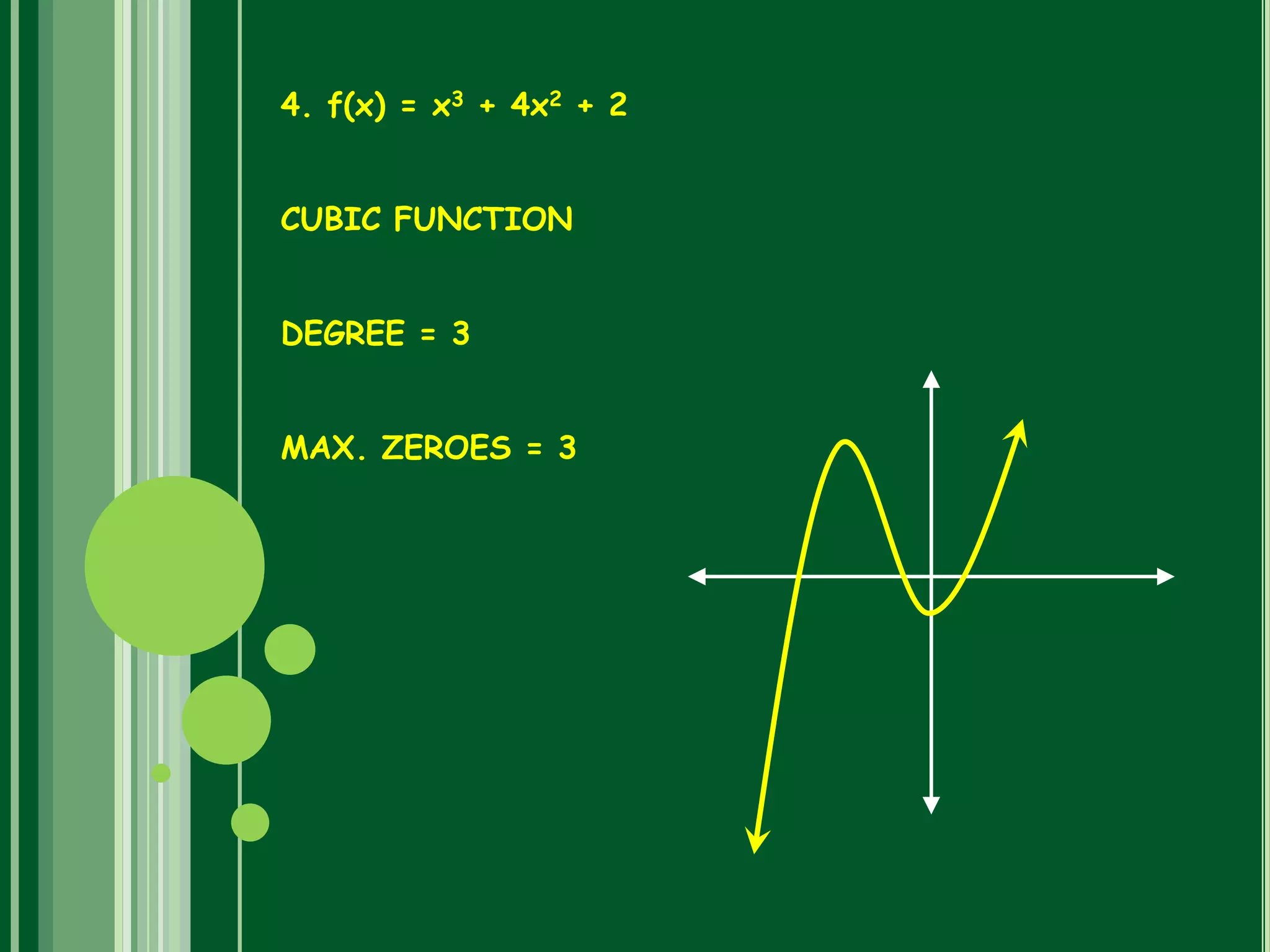
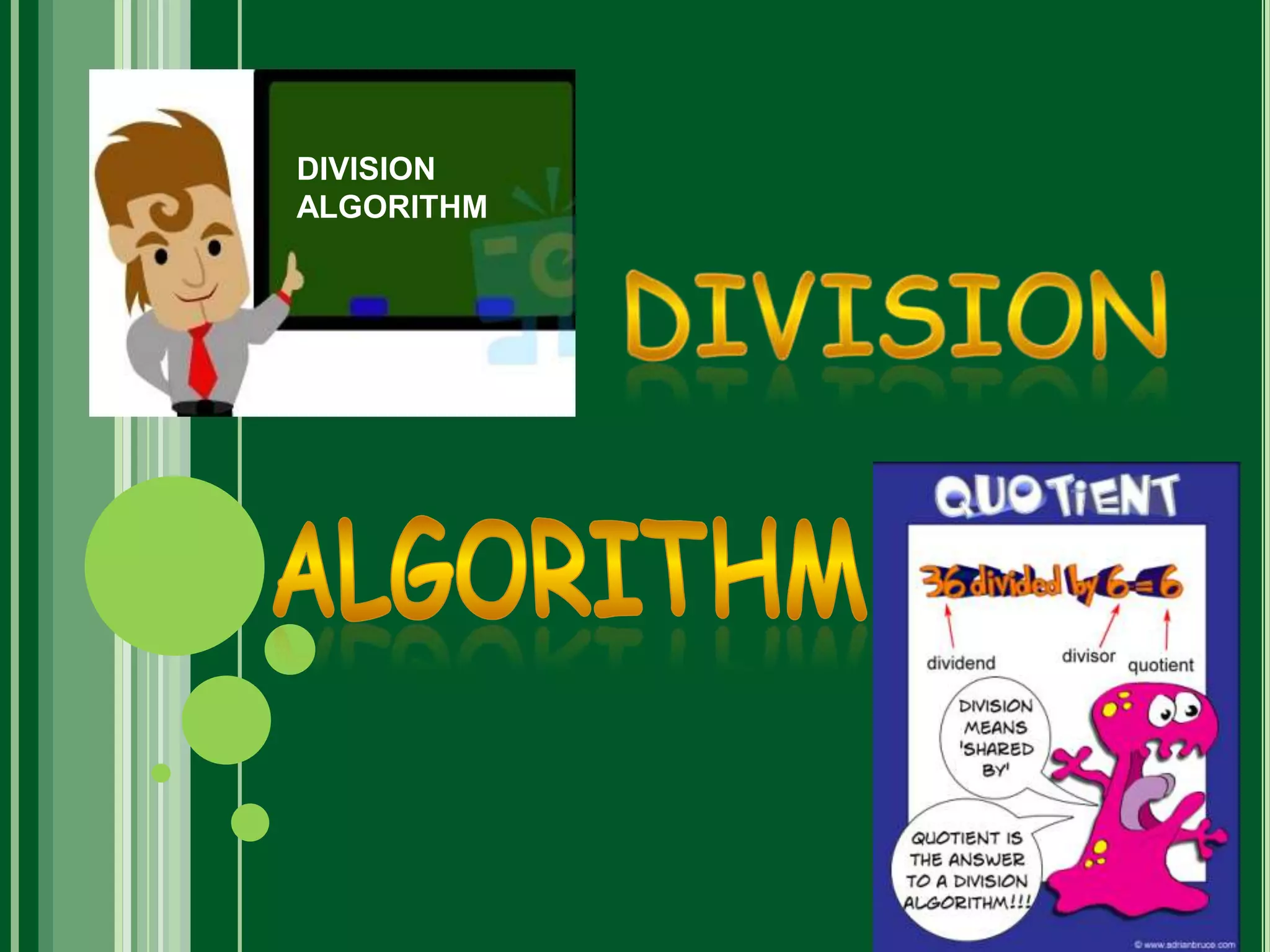
Polynomials are mathematical expressions constructed from variables and constants using addition, subtraction, multiplication, and exponents of whole numbers. They appear in many areas of mathematics and science. Polynomials can be used to form equations that model problems in various domains. They also define polynomial functions that are used in fields like physics, chemistry, economics, and social sciences. Polynomials are classified based on their degree, with linear polynomials having degree 1 and quadratic polynomials degree 2. The maximum number of zeroes a polynomial can have is equal to its degree.

2. In mathematics, a polynomial is an expression of finite length
constructed from variables and constants, using only the operations
of addition, subtraction, multiplication, and non-negative, whole-
number exponents. Polynomials appear in a wide variety of areas of
mathematics and science. For example, they are used to form
polynomial equations, which encode a wide range of problems, from
elementary word problems to complicated problems in the sciences;
they are used to define polynomial functions, which appear in
settings ranging from basic chemistry and physics to economics and
social science; they are used in calculus and numerical analysis to
approximate other functions.

3. Let x be a variable n, be a positive
integer and as, a1,a2,….an be constants
(real nos.)
Then, f(x) = anxn+ an-1xn-1+….+a1x+xo
 anxn,an-1xn-1,….a1x and ao are known as
the terms of the polynomial.
 an,an-1,an-2,….a1 and ao are their
coefficients.
For example:
• p(x) = 3x – 2 is a polynomial in variable x.
• q(x) = 3y2 – 2y + 4 is a polynomial in variable y.
• f(u) = 1/2u3 – 3u2 + 2u – 4 is a polynomial in variable u.

4. •A polynomial of degree 1 is called a Linear
Polynomial. Its general form is ax+b where a is not
equal to 0
•A polynomial of degree 2 is called a Quadratic
Polynomial. Its general form is ax3+bx2+cx, where a
is not equal to zero
•A polynomial of degree 3 is called a Cubic
Polynomial. Its general form is ax3+bx2+cx+d,
where a is not equal to zero.
•A polynomial of degree zero is called a Constant
Polynomial

5. LINEAR POLYNOMIAL
For example:
p(x) = 4x – 3, q(x) = 3y are linear
polynomials.
Any linear polynomial is in the form
ax + b, where a, b are real
nos. and a ≠ 0.
QUADRATIC POLYNOMIAL
For example:
f(x) = √3x2 – 4/3x + ½, q(w) = 2/3w2 + 4
are quadratic polynomials with real
coefficients.

6. For example:
If(x) = 7, g(x) = -3/2, h(x) = 2
are constant polynomials.
CUBIC POLYNOMIAL
CONSTANT POLYNOMIAL
For example:
f(x) = 9/5x3 – 2x2 + 7/3x _1/5
is a cubic polynomial in variable x.

7. If f(x) is a polynomial and y is
any real no. then real no.
obtained by replacing x by y in
f(x) is called the value of f(x)
at x = y and is denoted by f(x).
VALUE OF POLYNOMIAL
ZEROES OF POLYNOMIAL
A real no. x is a zero of the
polynomial f(x),is f(x) = 0
Finding a zero of the
polynomial means solving
polynomial equation f(x) = 0.

8. 1. f(x) = 3
CONSTANT FUNCTION
DEGREE = 0
MAX. ZEROES = 0

9. 2. f(x) = x + 2
LINEAR FUNCTION
DEGREE =1
MAX. ZEROES = 1

10. 3. f(x) = x2 + 3x + 2
QUADRATIC FUNCTION
DEGREE = 2
MAX. ZEROES = 2
These curves are also
called as parabolas

11. 4. f(x) = x3 + 4x2 + 2
CUBIC FUNCTION
DEGREE = 3
MAX. ZEROES = 3

13. α + β = - coefficient of x
Coefficient of x2
= - b
a
αβ = constant term
Coefficient of x2
= c
a

14. α + β + γ = -Coefficient of x2 = -b
Coefficient of x3 a
αβ + βγ + γα = Coefficient of x =
c
Coefficient of x3 a
αβγ = - Constant term = d
Coefficient of x3 a

15. DIVISION
ALGORITHM

16. •If f(x) and g(x) are
any two polynomials
with g(x) ≠ 0,then we
can always find
polynomials q(x), and
r(x) such that :
F(x) = q(x) g(x) +
r(x),
Where r(x) = 0 or
degree r(x) < degree
g(x)
•ON VERYFYING THE
DIVISION ALGORITHM
FOR POLYNOMIALS.
•ON FINDING THE
QUOTIENT AND
REMAINDER USING
DIVISION ALGORITHM.
•ON CHECKING WHETHER
A GIVEN POLYNOMIAL IS
A FACTOR OF THE OTHER
POLYNIMIAL BY APPLYING
THEDIVISION
ALGORITHM
•ON FINDING THE
REMAINING ZEROES OF A
POLYNOMIAL WHEN SOME
OF ITS ZEROES ARE GIVEN.