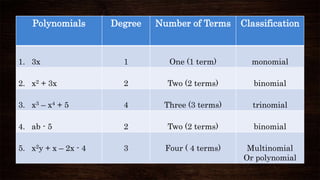
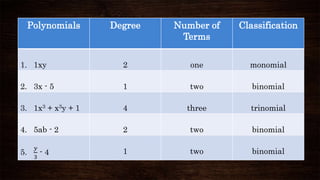
Polynomials are algebraic expressions with whole number exponents. A polynomial can be classified based on the number of terms as a monomial, binomial, trinomial, or multinomial. It can also be classified based on degree, which is the highest sum of exponents of variables in any term. Polynomials can be added or subtracted by combining like terms, where like terms have the same variables and exponents. Unlike terms are kept separate when adding or subtracting polynomials.

2. Polynomials
Polynomials are special kinds of algebraic expressions. These
expressions with a restriction that the exponents of a variables must be
whole numbers. A polynomial is a positive integral exponent.
The following are the restrictions of a polynomial:
• 1. No negative and fractional exponent in the variable
• 2. No variable under the radical sign (no variable serves as a
radicand 𝑥)
• 3. No variable in the denominator
2
𝑥

3. Polynomial Not Polynomial
x2
x-2
(the exponent of variable is negative)
y3
𝑦
1
3
(the exponent of the variable is a fraction)
y 5
5 𝑦
(the variable is under the radical sign)
3x
3𝑥
(the variable is under the radical sign)
𝑥
2
2
𝑥
(because the variable is at the denominator)

4. Identify whether is a polynomial or not.
Expression
1. 2x = P 6. a 2 = P
2. 3xy = P 7.
2𝑥
𝑦
= Not
3. x-3 = Not 8. -y = P
4. x + 2-3 = P 9. x + 3-2 = P
5. a3 – 5 = P 10.
𝑚𝑛
2
= P

5. A. Classifying Polynomials According to
the Number of Terms
• term – an element in a polynomial separated by plus or minus
sign
Example Number of Terms Type of Polynomial
2x one (1) monomial
2a + b2 two (2) binomial
2r – 4s + 2 three (3) trinomial
2x3 + x2 + 5x - 12 more than 3 terms multinomial/polynomial

6. Polynomial No. of Terms Classification
1. xy one monomial
2. a + b - c three trinomial
3. x2 - 6 two binomial
4. x + xy – y + z four multinomial/polynomial
5. 7 – 3a + c three Trinomial

7. B. Classification of Polynomial According to Degree
– Degree – highest exponent in a term
–If a polynomial has only one variable, its degree is equal to the
highest power appearing in any of the terms.
– If the polynomial has more than one variable, its degree is equal
to the highest sum of the exponents of the variable in any of the
terms.
–A polynomial of a non-zero constant is considered to be a
polynomial of degree zero. The constant zero is called a polynomial
but without any degree.

8. Example:
Polynomial Degree
2x4 4
3a3 + 4a2
(exponent 3 is higher than exponent 2) 3
xy3
(Exponent 1 in variable x plus exponent 3 in y.
So, 1 + 3 = 4)
4
2a3b2c – bc2
(Exponent 3 in variable a, plus exponent 2 in variable b,
plus exponent 1 in variable c. So, 3 + 2 + 1 = 6)
6
4x 1
-2 0

9. Polynomials Degree Number of Terms Classification
1. 3x 1 One (1 term) monomial
2. x2 + 3x 2 Two (2 terms) binomial
3. x3 – x4 + 5 4 Three (3 terms) trinomial
4. ab - 5 2 Two (2 terms) binomial
5. x2y + x – 2x - 4 3 Four ( 4 terms) Multinomial
Or polynomial

10. Polynomials Degree Number of
Terms
Classification
1. 1xy 2 one monomial
2. 3x - 5 1 two binomial
3. 1x3 + x3y + 1 4 three trinomial
4. 5ab - 2 2 two binomial
5.
𝑦
3
- 4 1 two binomial

11. Addition and Subtraction of Polynomials
Coefficient – is the numerical and literal factor of a term.
Examples:
1. 3x
3 = numerical coefficient
x = literal coefficient
2. 4xy
4 = numerical coefficient
xy = literal coefficient

12. Like or similar terms are two or more terms that have
same literal coefficient or two or more terms that contain
exactly the same variables and exponents.
In adding or subtracting polynomial with like terms, simply add
or subtract the numerical coefficients and copy the literal
coefficient.
Examples:
1. 2x + 3x = (2 + 3)x = 5x
2. y + 2y = (1 + 2)y = 3y
3. 4x2 – 3x2 = (4 – 3)x2 = 1x2 = x2
4. 5b – 7b = (5 – 7)b = -2b
5. 4xy + 2xy + 5xy = (4 + 2 + 5)xy = 11xy

13. Unlike terms
Examples:
1. 2x + y = 2x + y
2. 4b – 3 = 4b – 3
3. 3x – 4b = 3x – 4b
4. 5x – 3x + y = (5x – 3x) + y = 2x + y
5. x + 5 – 2 = x + (5 – 2) = x + 3
6. y – x + 2y = -x + (y + 2y) = -x + 3y = 3y – x