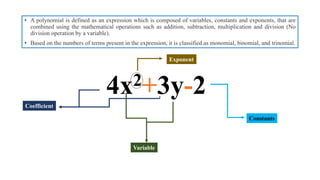
Polynomials are algebraic expressions consisting of variables, constants, and exponents combined using operations like addition, subtraction, multiplication, and division. They are classified based on the number of terms as monomials, binomials, or trinomials. The degree of a polynomial refers to the highest exponent present. Common polynomial operations include adding and subtracting like terms, multiplying polynomials according to distributive properties, and using long division to divide polynomials. Division of polynomials does not always result in another polynomial.

1. POLYNOMIALS
RAHUL JARARIYA

2. What is Polynomial?
Definition - Polynomials are algebraic expressions that consist of variables and
coefficients. Variables are also sometimes called indeterminates.
We can perform arithmetic operations such as addition, subtraction, multiplication and
also positive integer exponents for polynomial expressions but not division by variable.
Many Terms
Many terms
For example:
X2 + x - 12

3. • A polynomial is defined as an expression which is composed of variables, constants and exponents, that are
combined using the mathematical operations such as addition, subtraction, multiplication and division (No
division operation by a variable).
• Based on the numbers of terms present in the expression, it is classified as monomial, binomial, and trinomial.
4x2+3y-2
Constants
Coefficient
Variable
Exponent

4. DEGREE OF THE POLYNOMIAL
Polynomial Degree Example
Constant or Zero Polynomial 0 6
Linear Polynomial 1 3x+1
Quadratic Polynomial 2 6x
2
+x+1
Cubic Polynomial 3 6x
3
+4x
2
+3x+1
Quartic Polynomial 4 6x
4
+3x
3
+3x
2
+2x+1
Notation
The polynomial function is denoted by P(x)
where x represents the variable. For example,
P(x) = x2-5x+11
If the variable is denoted by s, then the
function will be P(s)
Terms of a Polynomial
The terms of polynomials are the parts of the equation which are generally
separated by “+” or “-” signs. So, each part of a polynomial in an equation is a
term. For example, in a polynomial, say, 2x2 + 5x +4, the number of terms will be
3. The classification of a polynomial is done based on the number of terms in it.
Example:
Find the degree of the polynomial 6s4+
3s2+ 5s +19
Solution:
The degree of the polynomial is 4.

5. Types of Polynomials
• Polynomials are of 3 different types and are classified based on the number of terms in it. The three types of polynomials are:
• Monomial
• Binomial
• Trinomial
• These polynomials can be combined using addition, subtraction, multiplication, and division but is never division by a variable. A few
examples of Non Polynomials are: 1/x+2, x-3
Monomial Binomial Trinomial
One Term Two terms Three terms
Example: x, 3y, 29 | x/2 Example: x2+x | x3-2x | y+2 Example: x2+2x+20

6. Polynomial Operations
There are four main polynomial operations which are:
•Addition of Polynomials
•Subtraction of Polynomials
•Multiplication of Polynomials
•Division of Polynomials
Each of the operations on polynomials is explained below using solved examples.
Addition of Polynomials
To add polynomials, always add the like terms, i.e. the terms having the same variable and power. The addition
of polynomials always results in a polynomial of the same degree. For example,
Example: Find the sum of two polynomials: 5x3+3x2y+4xy−6y2, 3x2+7x2y−2xy+4xy2−5
Solution:
First, combine the like terms while leaving the unlike terms as they are. Hence,
(5x3+3x2y+4xy−6y2)+(3x2+7x2y−2xy+4xy2−5)
= 5x3+3x2+(3+7)x2y+(4−2)xy+4xy2−6y2−5
= 5x3+3x2+10x2y+2xy+4xy2−6y2−5

7. Subtraction of Polynomials
Subtracting polynomials is similar to addition, the only difference being the type of operation. So, subtract the
like terms to obtain the solution. It should be noted that subtraction of polynomials also results in a polynomial
of the same degree.
Example: Find the difference of two polynomials: 5x3+3x2y+4xy−6y2, 3x2+7x2y−2xy+4xy2−5
Solution:
First, combine the like terms while leaving the unlike terms as they are. Hence,
(5x3+3x2y+4xy−6y2)-(3x2+7x2y−2xy+4xy2−5)
= 5x3-3x2+(3-7)x2y+(4+2)xy-4xy2−6y2+5
= 5x3-3x2-4x2y+6xy-4xy2−6y2+5
Multiplication of Polynomials
Two or more polynomial when multiplied always result in a polynomial of higher degree (unless one of them is
a constant polynomial). An example of multiplying polynomials is given below:
Example: Solve (6x−3y)×(2x+5y)
Solution:
⇒ 6x ×(2x+5y)–3y × (2x+5y) ———- Using distributive law of multiplication
⇒ (12x2+30xy) – (6yx+15y2) ———- Using distributive law of multiplication
⇒12x2+30xy–6xy–15y2 —————– as xy = yx
Thus, (6x−3y)×(2x+5y)=12x2+24xy−15y2

8. Division of Polynomials
Division of two polynomial may or may not result in a polynomial. Let us study below the division of polynomials in
details. To divide polynomials, follow the given steps:
Polynomial Division Steps:
If a polynomial has more than one term, we use long division method for the same. Following are the steps for it.
1.Write the polynomial in descending order.
2.Check the highest power and divide the terms by the same.
3.Use the answer in step 2 as the division symbol.
4.Now subtract it and bring down the next term.
5.Repeat step 2 to 4 until you have no more terms to carry down.
6.Note the final answer, including remainder, will be in the fraction form (last subtract term).
Polynomial Division:
(7s3+2s2+3s+9) ÷ (5s2+2s+1)
(7s3+2s2+3s+9)/(5s2+2s+1)
This cannot be simplified. Therefore, division of these polynomial do not result in a Polynomial.
Example

9. THANK YOU