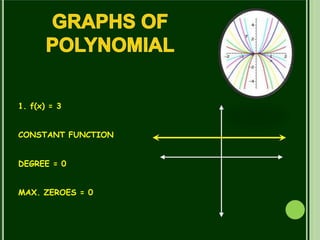
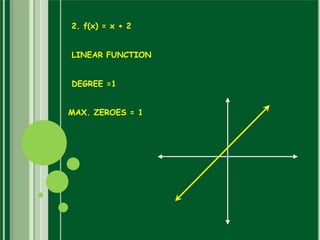
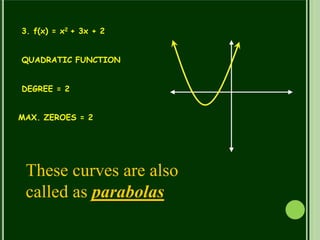
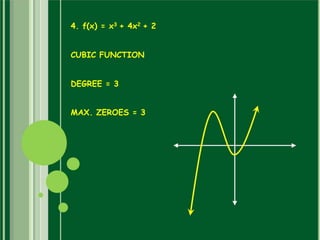
This document discusses polynomials. It defines a polynomial as an expression constructed from variables and constants using addition, subtraction, multiplication, and exponents. Polynomials appear in many areas of mathematics and science. The document then discusses the terms, coefficients, and different types of polynomials including linear, quadratic, cubic, and constant polynomials. It also discusses the degree and maximum number of zeroes of each type of polynomial. Finally, it discusses using the division algorithm to find quotients, remainders, and factors of polynomials.

1. SAINIK SCHOOL GOPALGANJ
CHAPTER : TWO
CHAPTER NAME : POLYNOMIALS
CLASS : 9

3. In mathematics, a polynomial is an expression of finite length
constructed from variables and constants, using only the operations
of addition, subtraction, multiplication, and non-negative, whole-
number exponents. Polynomials appear in a wide variety of areas of
mathematics and science. For example, they are used to form
polynomial equations, which encode a wide range of problems, from
elementary word problems to complicated problems in the sciences;
they are used to define polynomial functions, which appear in
settings ranging from basic chemistry and physics to economics and
social science; they are used in calculus and numerical analysis to
approximate other functions.

4. Let x be a variable n, be a positive
integer and as, a ,a ,….a be constants
1 2 n
(real nos.)
Then, f(x) = a xn+ a xn-1+….+a x+x
n n-1 1 o
 a xn,a xn-1,….a x and a are known as
n n-1 1 o
the terms of the polynomial.
 a ,a ,a ,….a and a are their
n n-1 n-2
coefficient
s.
1 o
For example:
• p(x) = 3x – 2 is a polynomial in variable x.
• q(x) = 3y2 – 2y + 4 is a polynomial in variable y.
• f(u) = 1/2u3 – 3u2 + 2u – 4 is a polynomial in variable u.

5. •A polynomial of degree 1 is called a Linear
Polynomial. Its general form is ax+b where a is not
equal to 0
•A polynomial of degree 2 is called a Quadratic
Polynomial. Its general form is ax3+bx2+cx, where a
is not equal to zero
•A polynomial of degree 3 is called a Cubic
Polynomial. Its general form is ax3+bx2+cx+d,
where a is not equal to zero.
•A polynomial of degree zero is called a Constant
Polynomial

6. LINEAR POLYNOMIAL
For example:
p(x) = 4x – 3, q(x) = 3y are linear
polynomials.
Any linear polynomial is in the form
ax + b, where a, b are real
nos. and a ≠ 0.
QUADRATIC POLYNOMIAL
For example:
f(x) = √3x2 – 4/3x + ½, q(w) = 2/3w2 + 4
are quadratic polynomials with real
coefficients.

7. CUBIC POLYNOMIAL
For example:
f(x) = 9/5x3 – 2x2 + 7/3x _1/5
is a cubic polynomial in variable x.
CONSTANT POLYNOMIAL
For example:
If(x) = 7, g(x) = -3/2, h(x) = 2
are constant polynomials.

8. VALUE OF POLYNOMIAL
If f(x) is a polynomial and y is
any real no. then real no.
obtained by replacing x by y in
f(x) is called the value of f(x)
at x = y and is denoted by f(x).
ZEROES OF POLYNOMIAL
A real no. x is a zero of the
polynomial f(x),is f(x) = 0
Finding a zero of the
polynomial means solving
polynomial equation f(x) = 0.

9. 1. f(x) = 3
CONSTANT FUNCTION
DEGREE = 0
MAX. ZEROES = 0

10. 2. f(x) = x + 2
LINEAR FUNCTION
DEGREE =1
MAX. ZEROES = 1

11. 3. f(x) = x2 + 3x + 2
QUADRATIC FUNCTION
DEGREE = 2
MAX. ZEROES = 2
These curves are also
called as parabolas

12. 4. f(x) = x3 + 4x2 + 2
CUBIC FUNCTION
DEGREE = 3
MAX. ZEROES = 3

14. α + β = - coefficient of x
Coefficient of x2
= -
b
a
αβ = constant term
Coefficient of x2
= c
a

15. α + β + γ = -Coefficient of x2
Coefficient of x3
= -b
a
αβ + βγ + γα =
c
Coefficient of x =
Coefficient of x3 a
αβγ = - Constant term
Coefficient of x3
= d
a

16. DIVISION
ALGORITHM

17. •ON FINDING THE
QUOTIENT AND
REMAINDER USING
DIVISION ALGORITHM.
•If f(x) and g(x) are
any two polynomials
with g(x) ≠ 0,then we
can always find
polynomials q(x), and
r(x) such that :
•ON CHECKING WHETHER
A GIVEN POLYNOMIAL IS
A FACTOR OF THE OTHER
POLYNIMIAL BY APPLYING
THEDIVISION
ALGORITHM
F(x) = q(x) g(x) +
r(x),
•
ON FINDING THE
Where r(x) = 0 or
degree r(x) < degree
gD(IxV)ISION ALGORITHM
FOR POLYNOMIALS.
REMAINING ZEROES OF A
POLYNOMIAL WHEN SOME
OF ITS ZEROES ARE GIVEN.
•ON VERYFYING THE