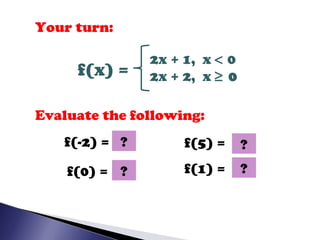
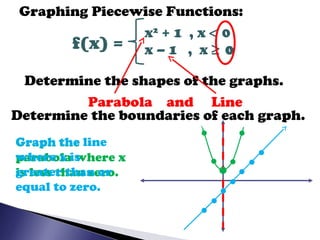
A piecewise function is defined by two or more separate functions over different parts of the domain. It can be evaluated by substituting values into the appropriate function based on the domain, and graphed by separately graphing each function over its domain and connecting the pieces. The document provides examples of evaluating and graphing piecewise functions, determining domains and ranges, and practicing evaluating additional functions.

2. Definition:Definition:
Piecewise FunctionPiecewise Function –a–a
function defined by two orfunction defined by two or
more functions over amore functions over a
specified domain.specified domain.

3. What do they look like?
f(x) =
x2
+ 1 , x < 0
x – 1 , x ≥ 0
You can EVALUATE piecewise
functions.
You can GRAPH piecewise functions.

4. Evaluating Piecewise Functions:
Evaluating piecewise functions is just
like evaluating functions that you are
already familiar with.
f(x) =
x2
+ 1 , x < 0
x – 1 , x ≥ 0
Let’s calculate f(2).
You are being asked to find y when
x = 2. Since 2 is ≥ 0, you will only
substitute into the second part of
the function.
f(2) = 2 – 1 = 1

5. f(x) =
x2
+ 1 , x < 0
x – 1 , x ≥ 0
Let’s calculate f(-2).
You are being asked to find y when
x = -2. Since -2 is < 0, you will only
substitute into the first part of
the function.
f(-2) = (-2)2
+ 1 = 5

6. Your turn:
f(x) =
2x + 1, x < 0
2x + 2, x ≥ 0
Evaluate the following:
f(-2) = -3?
f(0) = 2?
f(5) = 12?
f(1) = 4?

7. One more:
f(x) =
3x - 2, x < -2
-x , -2 ≤ x < 1
x2
– 7x, x ≥ 1
Evaluate the following:
f(-2) = 2?
f(-4) = -14?
f(3) = -12?
f(1) = -6?

8. Graphing Piecewise Functions:
f(x) =
x2
+ 1 , x < 0
x – 1 , x ≥ 0
Determine the shapes of the graphs.
Parabola and Line
Determine the boundaries of each graph.
Graph the
parabola where x
is less than zero. •
•
•
•
•
°
Graph the line
where x is
greater than or
equal to zero. •
•
•
•
•
•
•

9. •
•
•
•
•
•
3x + 2, x < -2
-x , -2 ≤ x < 1
x2
– 2, x ≥ 1
f(x) =
Graphing Piecewise Functions:
Determine the shapes of the graphs.
Line, Line, Parabola
Determine the boundaries of each graph.
°
•
•
•
•
•
•
°•
•
• •
•

10. Graphing Piecewise Functions
( )
x 4 x 4
2x
x 3 x
1
1
g x 5 4 x+ − ≤
− + >
 + < −
= ≤




Domain - ( ),−∞ ∞
Range - ( ), 7−∞

11. ( )
3 7 x 4
1
x 2 4 x 0
2
1
x 4
x
0 x 5
5 x 7
g
−
− −
− <
− − <



= 
<
< ≤ −
+ ≤ ≤
≤



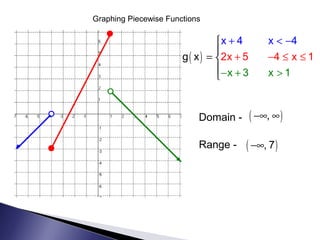
Domain - (-7, 7]
Range - (-4, -2), [-1, 4]

12. ( )
1
x 6 x 3
3
x 1 3 x 0h x
x 4 0 x 3
x 3 3 x 7

− − ≤ ≤ −
 + − < ≤= 
 + < <

− + ≤ ≤
Domain - [-6, 7]
Range - [-4, 2], (4, 7)

13. ( )
4 x 3
h x 2x 3 3 x 4
4x 7 x 6
≤ −

= + − < ≤
 − ≥

14. Piecewise Function – Domain and Range
Domain -
Range -
Domain - (-6, 7)
Range - [-1, 5 )
[-7, 7]
(-4.5,-1], [0, 4)

15. Domain -
Range -
Domain -
Range -
(-7, -1), (-1, 7]
[-1, 5), [6, 6]
(-7, 4), [5, 7)
[-7, -5), (-2, 7)

16. Domain -
Range -
Domain -
Range -
( ),−∞ ∞
( ], 4−∞
[-1, 5]
[-5, 3]