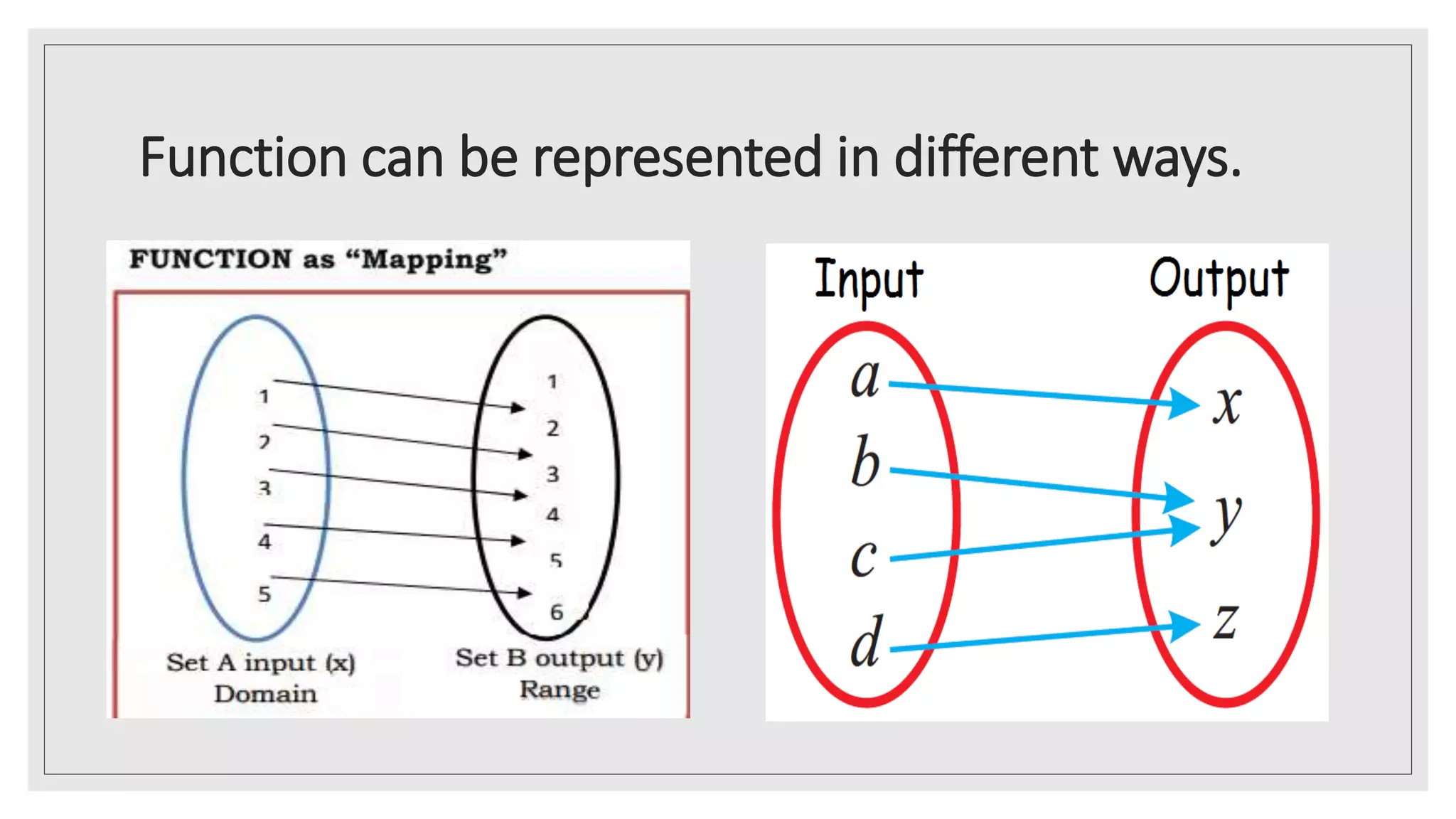
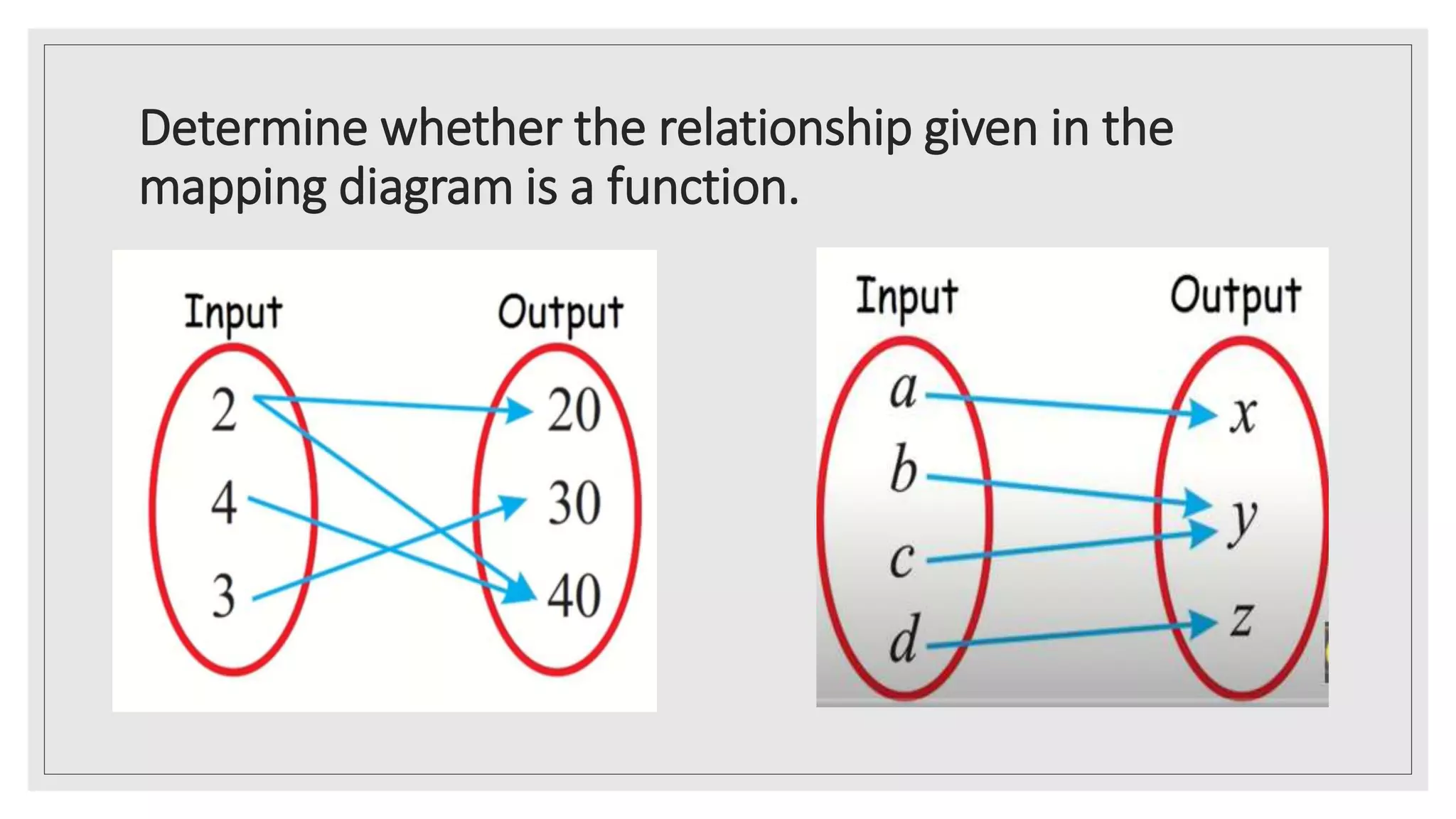
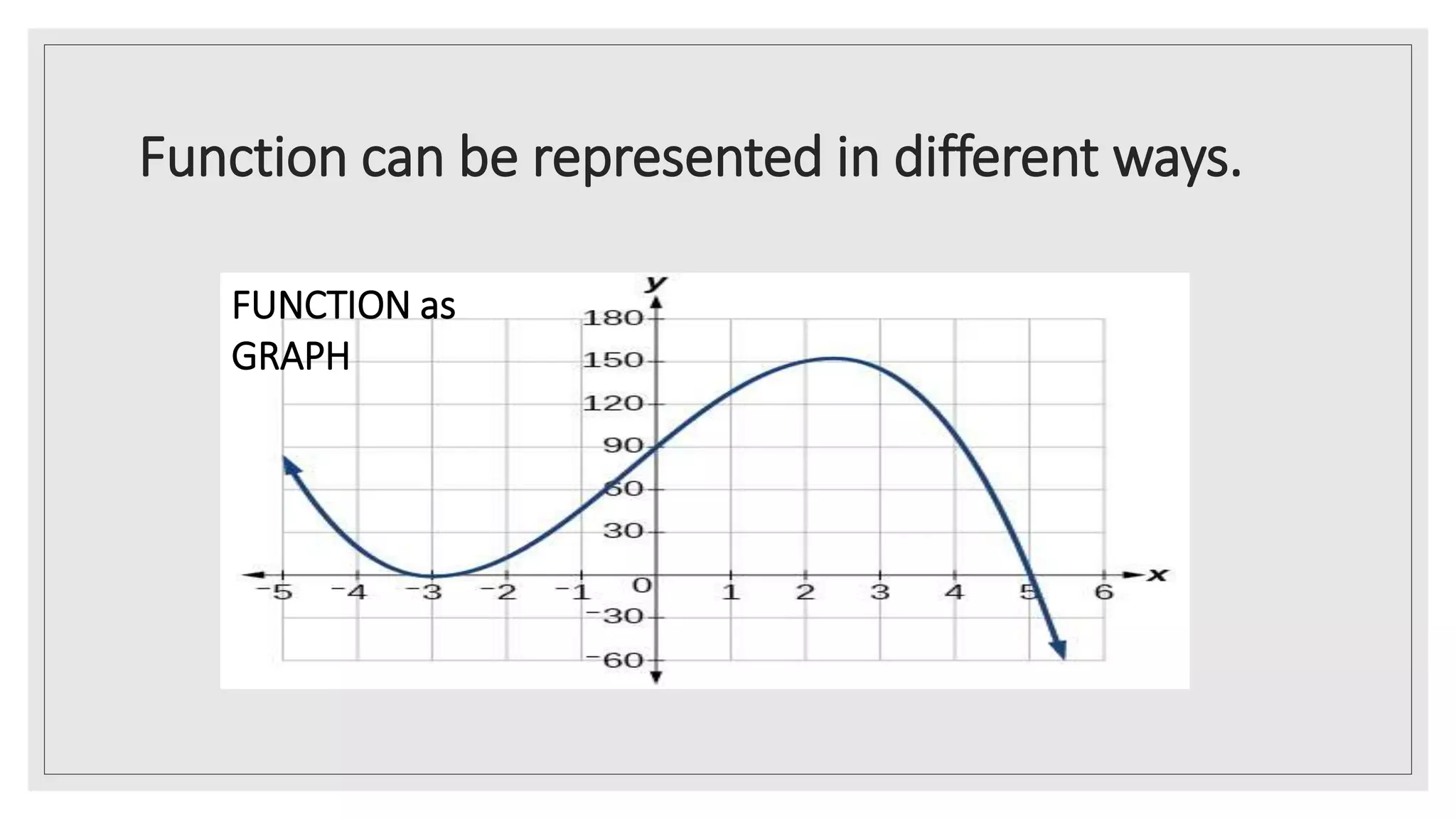
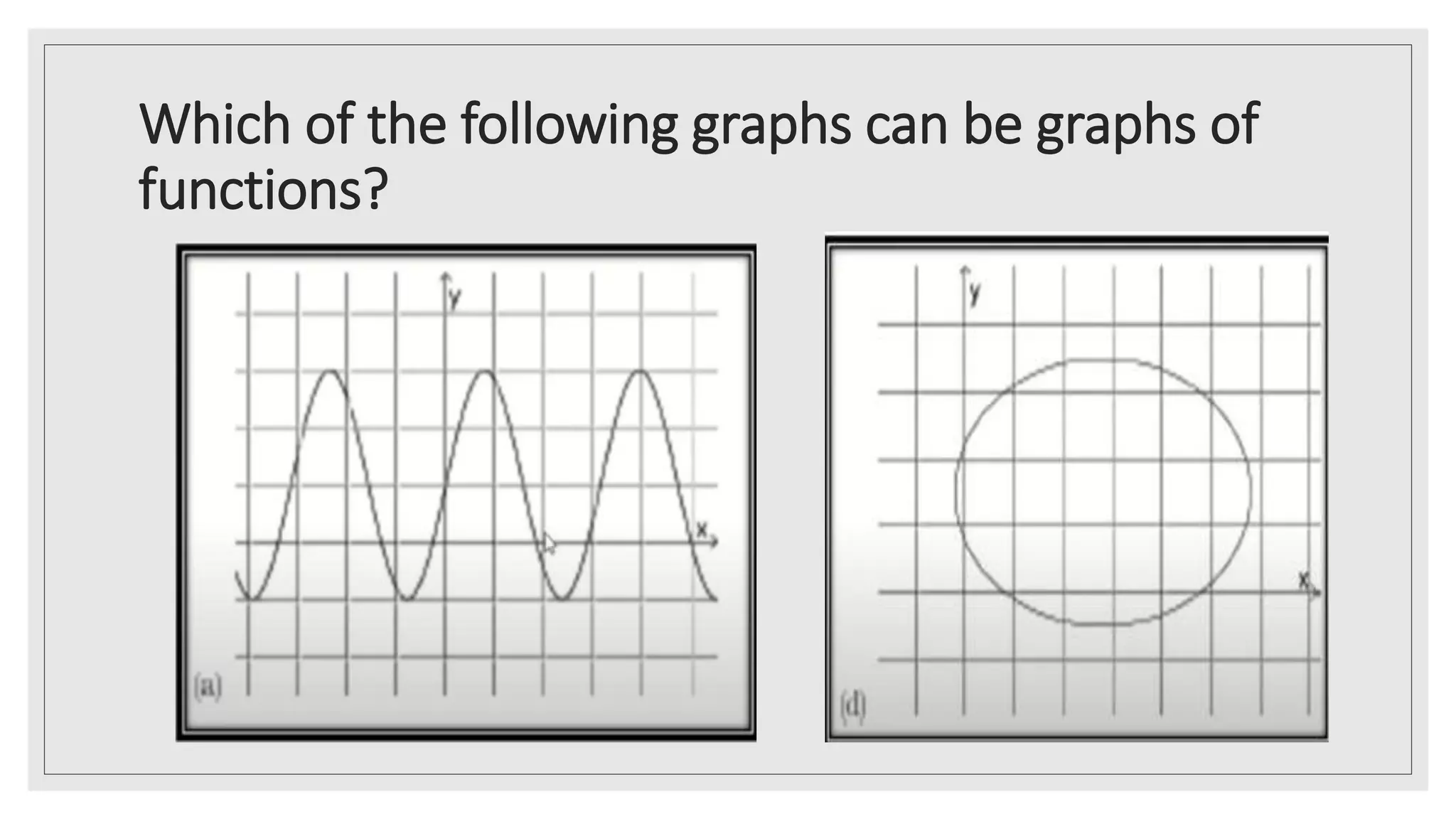
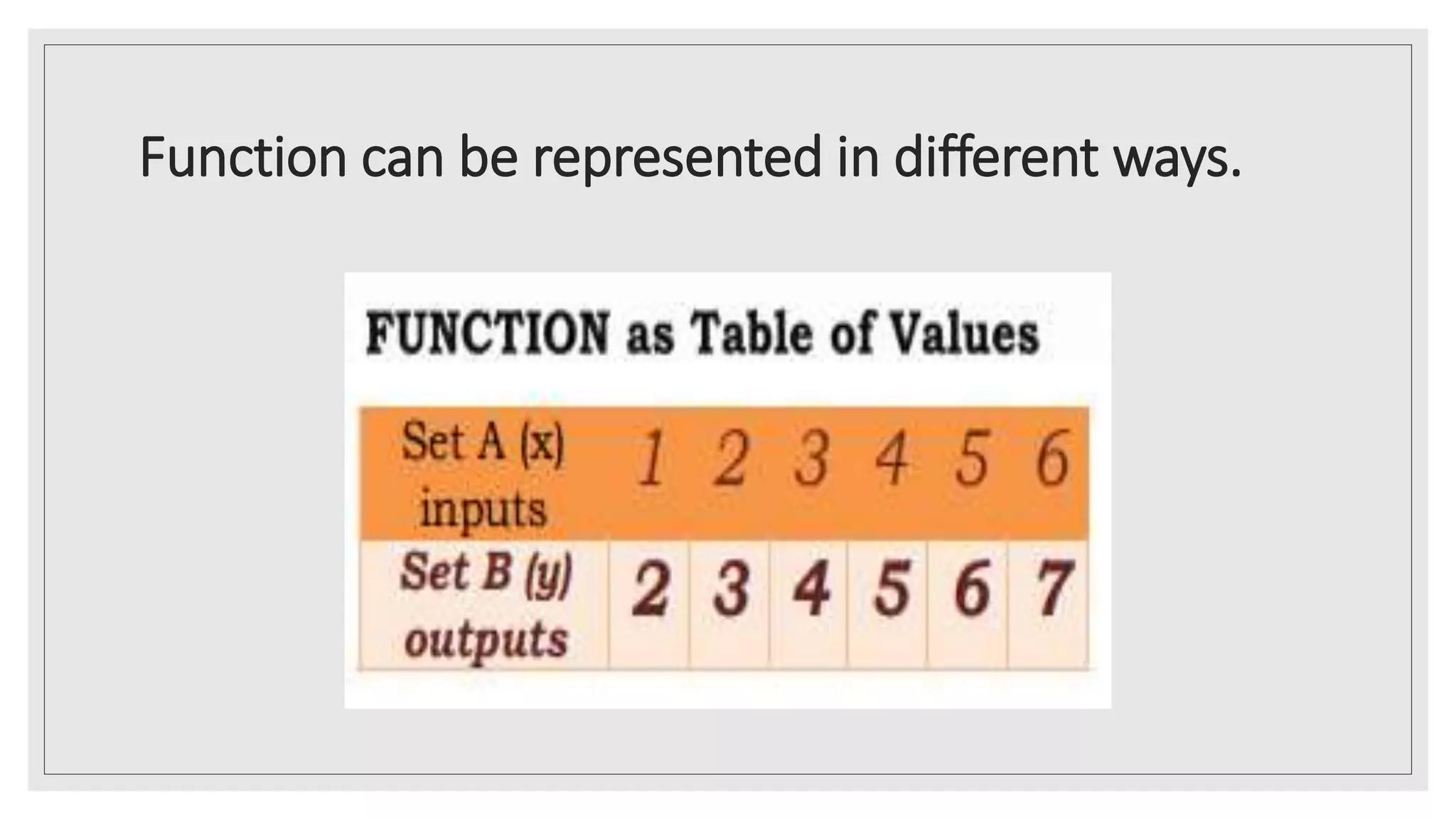
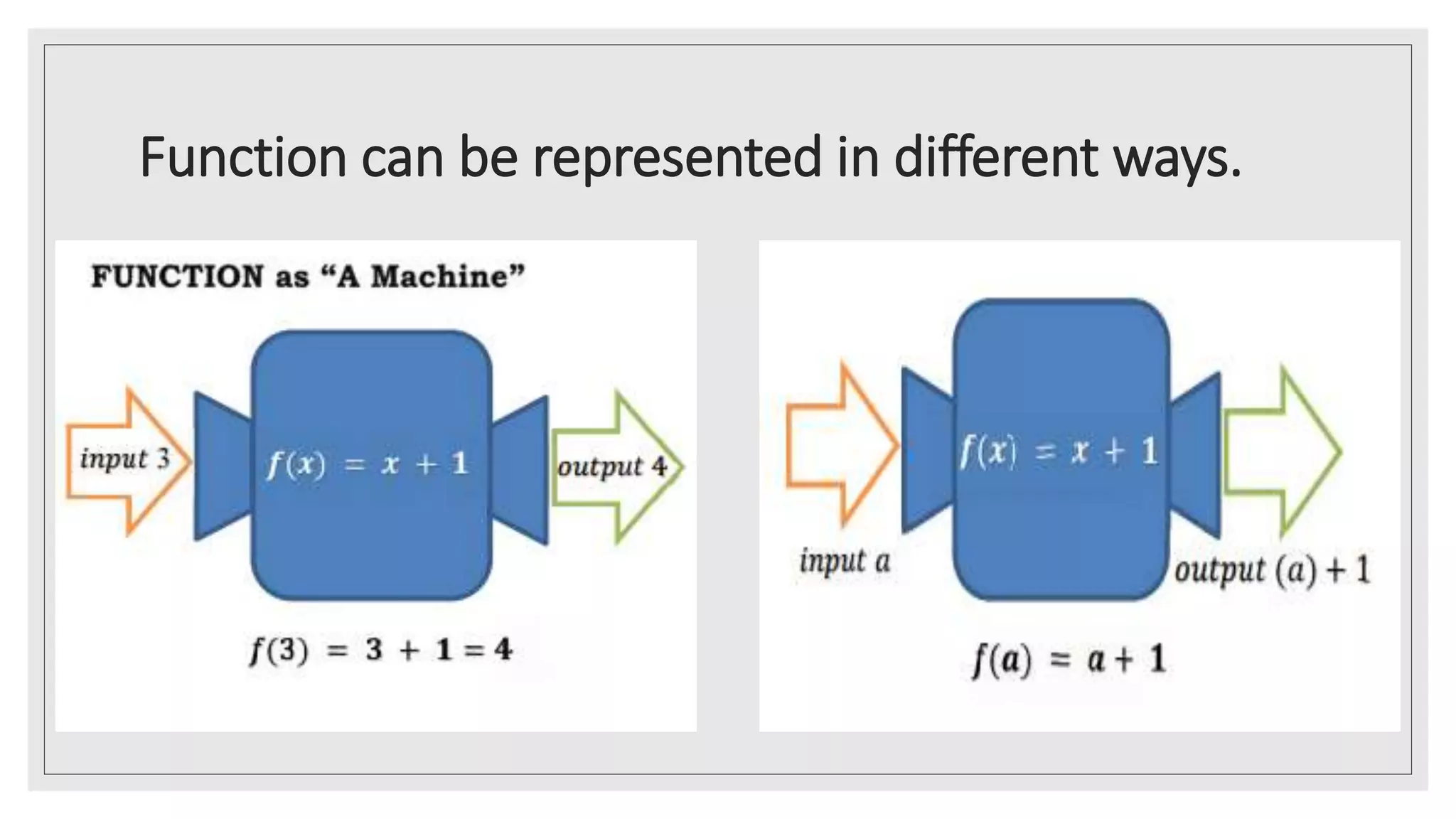
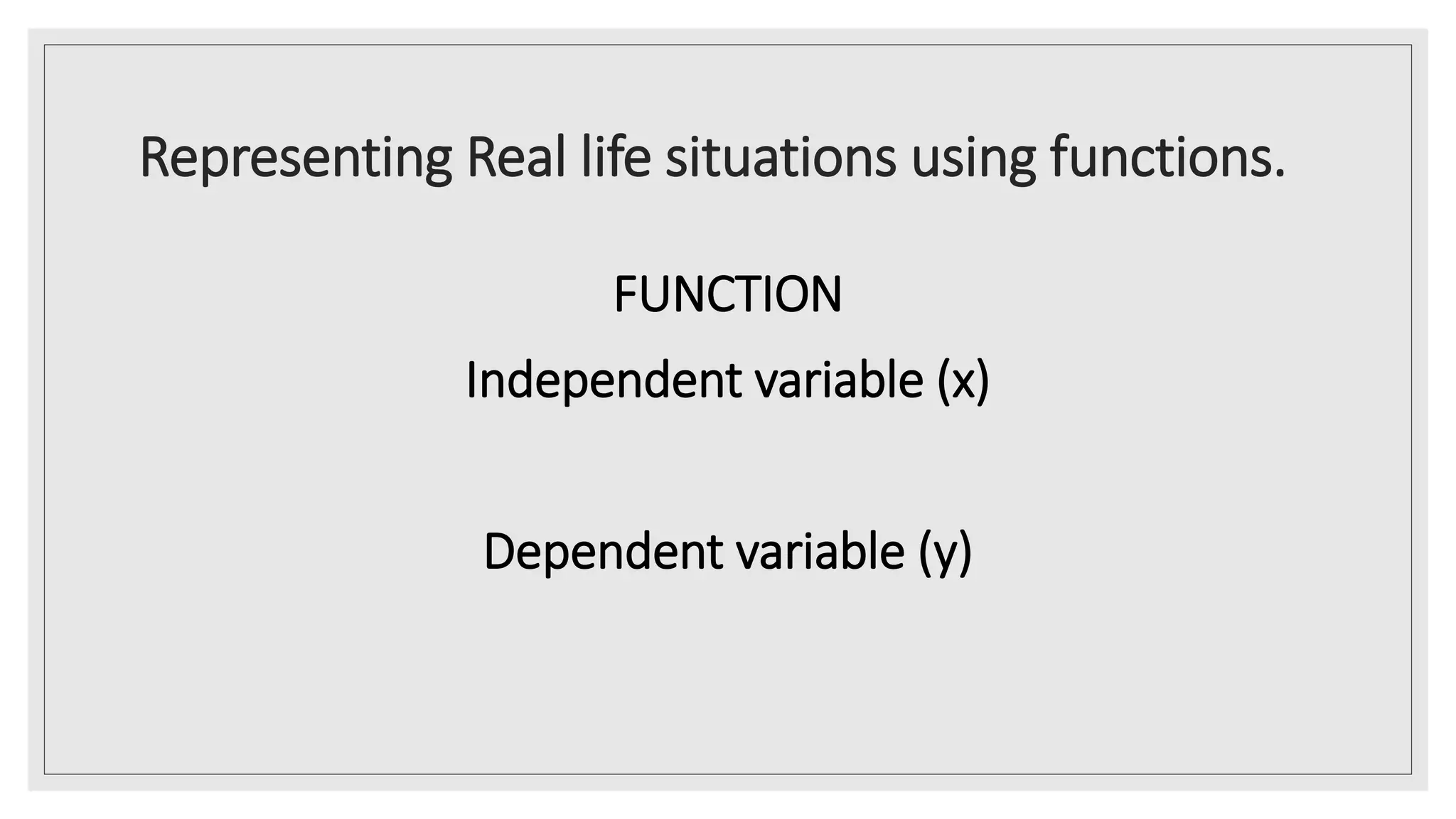
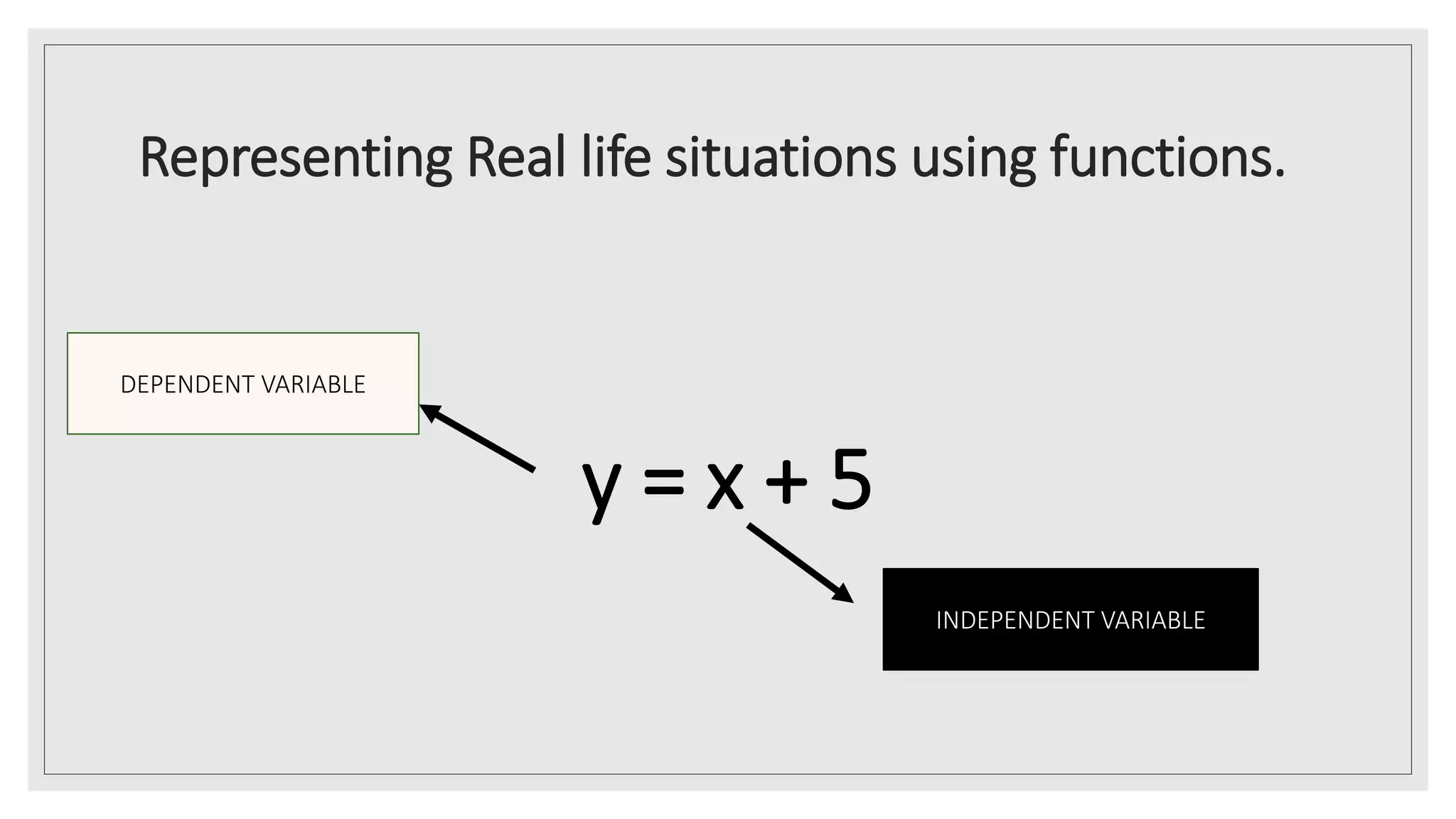
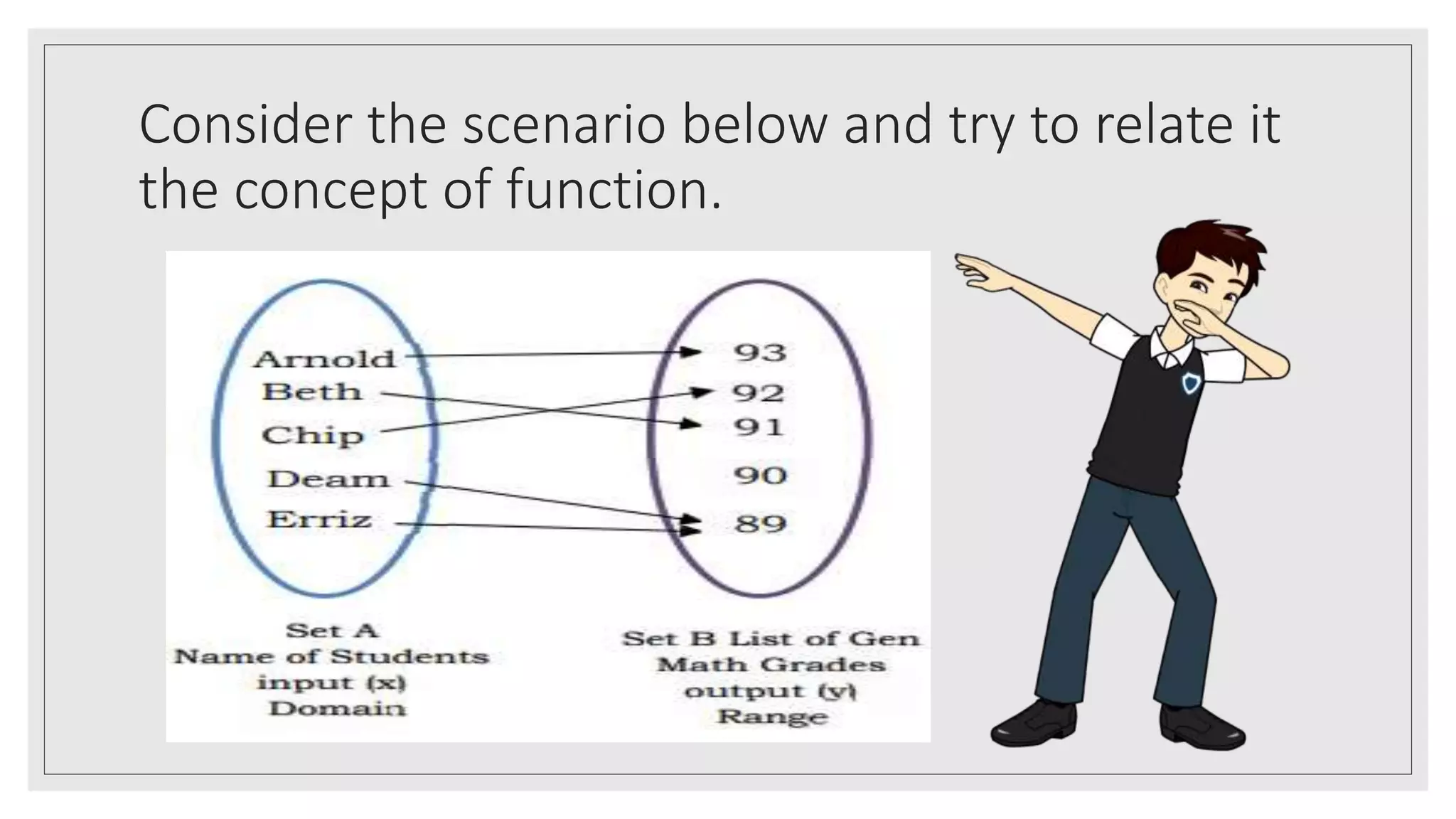
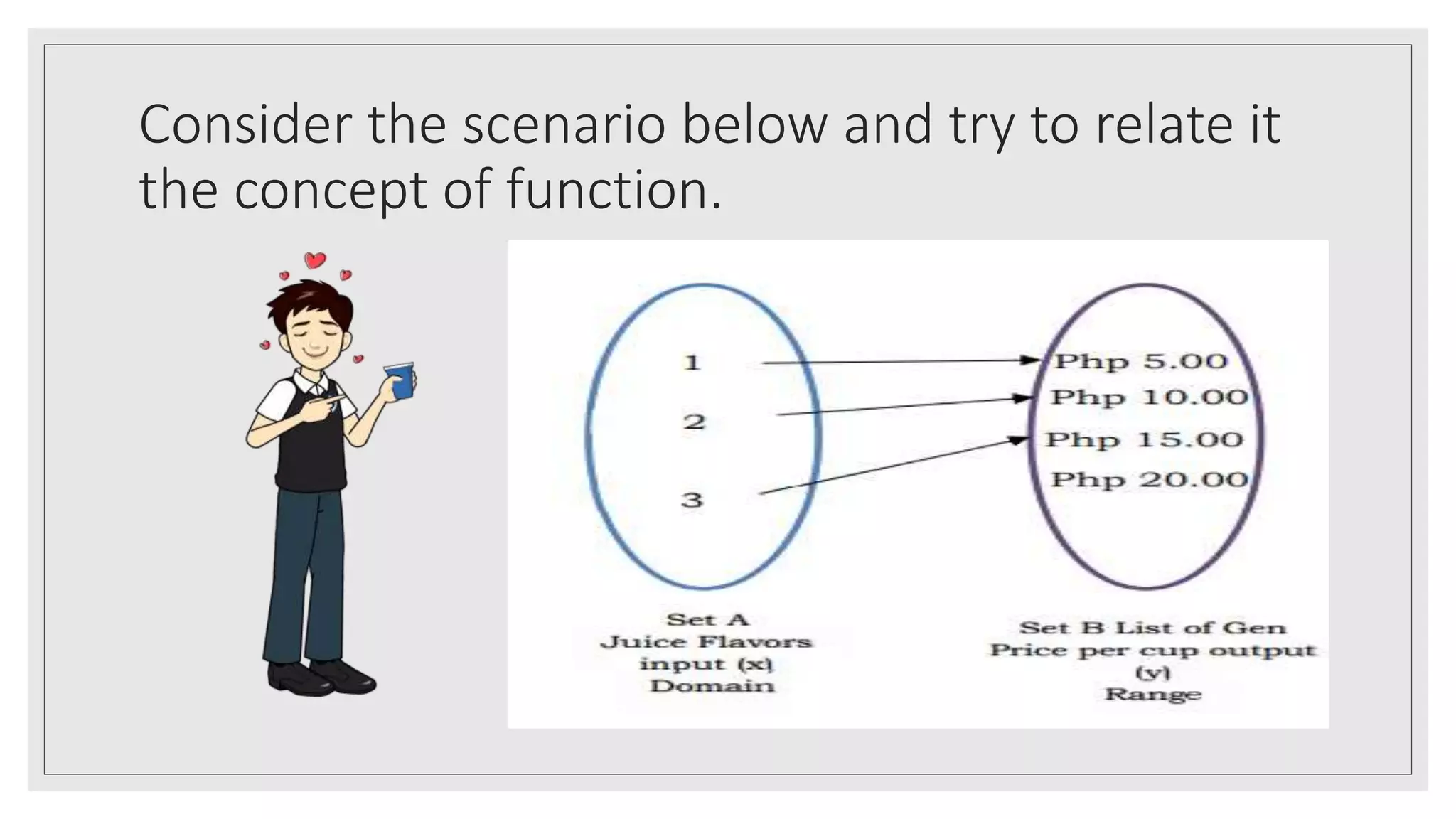
The document provides an overview of key concepts about functions for senior high school mathematics. It discusses representing real-life situations using functions, including piecewise functions. Different ways of representing functions are presented, such as graphs. Examples of relating scenarios to the independent and dependent variables of a function are given. The document also demonstrates representing real-life situations as mathematical function models and provides sample problems about piecewise functions.

1. GENERAL
MATHEMATICS
SENIOR HIGH SCHOOL

2. CHAPTER 1
Key Concepts of Functions

3. Accurately construct mathematical models to represent
real-life situations using functions.
PERFORMANCE STANDARD

4. Most Essential Learning Competencies
At the end of the lesson, you should be able to:
represents real-life situations using functions, including piece-
wise functions;
evaluates a function;
performs addition, subtraction, multiplication, division, and
composition of functions; and
solves problems involving functions.

5. LESSON 1
FUNCTIONS AS MODELS

6. Relation
◦It is a set of ordered pairs.
Example:
−2, 10 , −1, −7 , 0, −4 , 1, −1 , (2, −2)

7. What is Function?
Function is a mathematical relation
within two objects: an input and
output, and that the output is
related to the input by some rule.

8. Basic Concept and Representation of Function
A function 𝒇 from set A (input) to set B
(output) is a rule of correspondence that
assigns to each element x in the set A exactly
one element y in the set B

9. Basic Concept and Representation of Function
Each x can have only one y, but it CAN be
the same y as another x gets assigned to.

10. Function can be represented in different ways.

11. Which of the following relations are functions?

12. Function can be represented in different ways.

13. Determine whether the relationship given in the
mapping diagram is a function.

14. Function can be represented in different ways.
FUNCTION as
GRAPH

15. Which of the following graphs can be graphs of
functions?

16. Function can be represented in different ways.

17. Function can be represented in different ways.

18. Representing Real life situations using functions.
Function can be seen in real life situations and is
very useful in almost all walks of life, as it
interpret these scenarios in mathematical
models.

19. Representing Real life situations using functions.
FUNCTION
Independent variable (x)
Dependent variable (y)

20. Representing Real life situations using functions.
y = x + 5
INDEPENDENT VARIABLE
DEPENDENT VARIABLE

21. Consider the scenario below and try to relate it
the concept of function.
Scenario A
STEM 11-St. Augustine students of SJC list
down their grades in General Mathematics.
Basically, each student has only one grade for
General Mathematics, but more than one
student can get the same grade.

22. Consider the scenario below and try to relate it
the concept of function.

24. Consider the scenario below and try to relate it
the concept of function.
Scenario B
In our school canteen, all kinds of juices are worth Php 5.00
each cup. There is juice, pineapple juice, guava juice, chocolate
juice, buko juice, and many more to choose from.
Ana wants to buy 2 different juices, while Brenda wants to buy
3 different juices.

25. Consider the scenario below and try to relate it
the concept of function.

27. Sample Real-Life Scenario
Use the guide questions below in representing each real-life scenario
as a function model.
a. Which represents as the input 𝑥?
b. Which represents as the output 𝑓(𝑥)?
c. How will you represent the scenario into a function
model?

28. Sample A
◦Mr. Anniz noticed that his motorcycle
consumes 1 liter of gasoline from his home
going to Vista Mall which is 15 kilometers
apart.
◦Represent the total number of kilometers K(x)
in an x number of liters.

29. Sample B
◦ Romer transferred a three - leaf tomato
tree from a pot to the soil. The next
morning, Romer was surprised to see
three new leaves have sprouted. The
following day, he expected the tree to have
9 leaves, and he was right.

30. Sample C
◦ A car for hire can be rented for 3000 pesos
with an additional daily rate of 1500 pesos.
Represent the total rental fee 𝑅(𝑥) in an 𝑥
number of days.

31. Sample D
◦Represent the daily total earnings 𝑇(𝑥
) of an online video site considering
the 𝑥 number of views that costs 5
pesos per view.

32. Try This!
Represent the presented real-life situation as function models.
◦ Through the realization in the COVID-19 experiences, Kevin and Lena
both Senior High School students started savings for charity cost.
◦ Kevin sells paintings he made while Lena sells face masks. Kevin has an
initial savings of P30.00 pesos and saves P15.00 every day. While
Lena initially saves P40 pesos and saves P10.00 pesos every day.
◦ Represent the TOTAL EARNINGS E(x) in an x number of days.

33. Piecewise Function
A piecewise function is a
function made from
different functions over
different intervals

34. Sample Problem #1
◦Lara bought a P150 load good for a month. It includes 100
free text messages. Messages in excess of this charged P1
each.
◦Give a function c(m) representing the monthly cost
corresponding to the number of text messages m

36. Sample Problem #2
◦ In this time of pandemic, some businesses took action to adapt to the new
normal. Boyet, a computer shop owner, came up with an ingenious solution
which he called, “Rent a Comp”.
◦ The concept is to lend a computer, which is packed with a device that
computes or counts the time of usage, to a costumer. The renter needs to pay
an initial of Php 600.00 for a total of 500 hours, and an additional amount of 2
pesos for the excess time per hour.

38. ROMANS 12:4
For just as we have many members in one body and
all the members do not have the same function.

39. BE MATHIVATED!