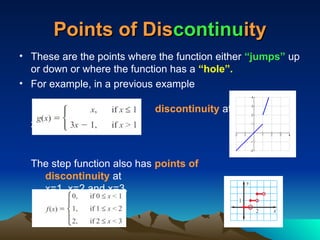
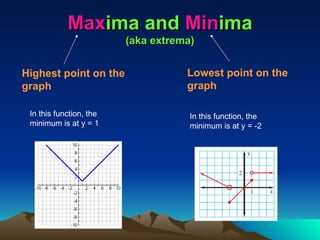
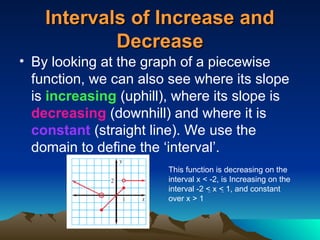
Piecewise functions consist of multiple equations, each applicable to different parts of the domain, requiring specific evaluations based on defined intervals. They can exhibit discontinuities where the function jumps or has holes, and the domain and range must be identified for proper evaluation. Additionally, features like the axis of symmetry and intervals of increase or decrease are crucial for understanding the behavior of these functions.

1. Evaluating Piecewise and
Evaluating Piecewise and
Step Functions
Step Functions

2. Evaluating Piecewise Functions
Evaluating Piecewise Functions
• Piecewise functions are functions defined
by at least two equations, each of which
applies to a different part of the domain
• A piecewise function looks like this:
Equations
Domain restrictions

3. Evaluating Piecewise Functions
Evaluating Piecewise Functions
• Steps to Evaluate Piecewise Functions
1. Look at the domain to see which equation to use
2. Plug in x-value
3. Solve! 
Ex. #1: Find
a. g(-2) and b. g(2)

4. Evaluating Piecewise Functions
Evaluating Piecewise Functions
Ex. #2
Which equation would we use to find; g(-5)? g(-2)?
g(1)?
16
1
)
5
(
2
)
5
(
)
5
( 2







g
1
1
)
2
(
2
)
2
(
)
2
( 2







g
0
)
1
(
1
)
1
( 2



g

5. Step Functions
Step Functions
Looks like a flight of stairs
An example of a step function:
Graphically, the equation would look like this:

6. Classwork/Homework
Classwork/Homework
• Evaluating WS

8. Domain and Range of Piecewise
Domain and Range of Piecewise
Functions
Functions
• Domain (x): the set of all input numbers -
will not include points where the
function(s) do not exist. The domain also
controls which part of the piecewise
function will be used over certain values of
x.
• Range (y): the set of all outputs.

9. Points of Dis
Points of Discontinu
continuity
ity
• These are the points where the function either “jumps” up
or down or where the function has a “hole”.
• For example, in a previous example
Has a point of discontinuity at
x=1
The step function also has points of
discontinuity at
x=1, x=2 and x=3.

10. Axis of Symmetry
Axis of Symmetry
• The vertical line that splits the equation in
half.
For the equation the
axis of symmetry is located at x = 1
1
1

x
y
This ‘axis of symmetry’ can be
found by identifying the x-
coordinate of the vertex (h,k), so
the equation for the axis of
symmetry would be x = h.

11. Max
Maxima and
ima and Min
Minima
ima
(aka extrema)
(aka extrema)
In this function, the
minimum is at y = 1
In this function, the
minimum is at y = -2
Highest point on the
graph
Lowest point on the
graph

12. Intervals of Increase and
Intervals of Increase and
Decrease
Decrease
• By looking at the graph of a piecewise
function, we can also see where its slope
is increasing (uphill), where its slope is
decreasing (downhill) and where it is
constant (straight line). We use the
domain to define the ‘interval’.
This function is decreasing on the
interval x < -2, is Increasing on the
interval -2 < x < 1, and constant
over x > 1

13. Classwork/Homework
Classwork/Homework
• Characteristics WS