The document discusses different types of solids and crystal structures. It begins by stating that everything around us is matter, which is made of molecules and exists in four main types. It then discusses crystalline and amorphous solids, and the key differences between them. Crystalline solids like metals can have either a single crystal or polycrystalline structure. The document also covers various crystal structures like simple cubic, body centered cubic, face centered cubic, and diamond cubic. It defines important concepts such as unit cell, lattice points, Miller indices, coordination number and packing factor.

2.  Everything we see around us is matter
 Matter is made of molecules
 Matter comes in Four main types

4. Solids can be classified as Crystalline Solids and
Amorphous (non-crystalline) Solids
 A crystalline solid can either be a single crystal or polycrystalline.
 In the case of single crystal the entire solid consists of only one crystal.
 Polycrystalline is an aggregate of many small crystals separated by
well defined boundaries.

5. Crystalline Amorphous
In each crystal, the atoms are arranged
in a regular periodic manner in all
three directions
In amorphous solid, the atoms are
arranged in a irregular manner
A crystal has regular shape and when
it is broken all broken pieces have the
same regular shape.
Amorphous solids do not possess any
regular shape
They have a sharp melting point They do not have a sharp melting
point. They have wide range of
melting points
The crystals have directional
properties and therefore called
anisotropic substances
These solids have no directional
properties and therefore called
isotropic substances
Examples:
1. Metallic crystals: Copper, Silver,
Aluminium, tungsten and
magnesium.
2. Non-metallic crystals: Ice,
Carbon, Diamond, Nacl
Examples:
Glass
Plastics
Rubber

6.  According to Hauy (1784) a crystal is built up by a number of
small crystals having the shape of the original crystal as a whole.
This led to the concept of space lattice or crystal lattice.
“A space lattice is defined as an infinite array
of points in three dimensions in which every
point has surroundings identical to that of every
other point in the array”

7. The unit cell is the smallest block from which entire crystal is built up
by repetition in three dimensions
The repeating unit assembly – atom or molecule, that is located at each
lattice point is called the basis. The basis is an assembly of atoms
identical in composition, arrangement and orientation.

8. In a crystal, the angles between X, Y and Z axes are known as
‘interfacial angles’. The angles α, β and γ are said to be interfacial
angles.
In order to represents lattice, the above three interfacial angles and the
corresponding intercepts are essential. These six parameters are said to
be ‘lattice parameters’. a, b and c are also said to be primitives.
The smallest possible unit cell of a lattice,
having lattice points at each of its eight
corners only. It consists of only one full atom.
If a unit cell consists of more than one
atom then it is not a primitive cell. It is call
non-primitive cell.

11. 14 Bravais lattices divided into seven crystal
systems
Crystal system Bravais lattices
1. Cubic P I F
2. Tetragonal P I
3. Orthorhombic P I F C
4. Hexagonal P
5. Trigonal P
6. Monoclinic P C
7. Triclinic P

13. Arrangement of lattice points in the unit cell
& No. of Lattice points / cell
Position of lattice points
Effective number of Lattice
points / cell
1 P 8 Corners = 8 x (1/8) = 1
2 I
8 Corners
+
1 body centre
= 1 (for corners) + 1 (BC)
3 F
8 Corners
+
6 face centres
= 1 (for corners) + 6 x (1/2)
= 4
4 C
8 corners
+
2 centres of opposite faces
= 1 (for corners) + 2x(1/2)
= 2

16. The distance between the centers of two nearest neighbouring atoms is
called nearest neighbour distance.
If ‘r’ is the radius of the atom, nearest neighbour distance is ‘2r’.
Atomic radius is defined as half the distance between the centers of the
nearest neighbouring atoms in a crystal.

17. Coordination number is defined as the number of equidistant nearest
neighbouring atoms to a particular atom in the given structure. For a
simple cubic unit cell, the coordination number is 6.
Atomic packing factor is the ratio of volume occupied by the atoms in
an unit cell (v) to the total volume of the unit cell (V). It is also called
packing fraction.
Number of atoms present in a unit cell × Volume of one atom
Packing Factor =
Total volume occupied by atoms in a unit cell
Total volume of the unit cell
Total volume of the unit cell
=

18. a
 The simplest and easiest structure to describe is the simple cubic
crystal structure.
 In a simple cubic lattice, there is one lattice point at each of the
eight corners of the unit cell. The atoms touch along cube edges.
Hence nearest neighbour distance , 2r = a
Lattice constant a = 2r
Hence atomic radius r = a/2

19.  Let us consider any corner atom.
 For this atom, there are four nearest
neighbours in its own plane.
 There is another nearest neighbour in a
plane which lies just above this atom and
yet another nearest neighbour in another
plane which lies just below this atom.
 Therefore, the total number of nearest
neighbours is six and hence,
The coordination number is 6

20. Thus, 52 % of the volume of the simple cubic unit cell is occupied
by atoms and the remaining 48 % volume of the unit cell is vacant.

21. 1. A body centered cubic (BCC) structure has
eight corner atoms and one body centered atom.
2. The diagrammatic representation of a BCC
structure is shown in Figure.
3. In BCC crystal structure, the atoms touch along
the diagonal of the body.
4. The total number of atoms present in a BCC
unit cell is 2.

22. A
4r a
H
G
F
E
D
C
B
For a BCC unit cell, the atomic radius
can be calculated from the Figure.
From the Figure, AH = 4r and DH = a
From the triangle ADH
AD2 + DH2 = AH2
To find AD, consider the ΔABD,
From the ΔABD,
AB2 + BD2 =AD2
a2 + a2 = AD2
AD2 = 2a2
AD =
(1)
Substituting AD, AH and DH
values in Eq. (1)
AD2 + DH2 = AH2
2a2 + a2 = (4r)2
16r2 = 3a2
r2 = (3/16) a2
r = ( / 4)a

23.  The coordination number of a BCC unit cell
can be calculated as follows.
 Let us consider a body centered atom.
 The nearest neighbour for a body centered
atom is a corner atom.
 A body centered atom is surrounded by
eight corner atoms.
 There the coordination number of BCC unit
cell is Eight.
The coordination number is 8

24. Thus, 68 % of the volume of the BCC unit cell is occupied by
atoms and the remaining 32 % volume of the unit cell is vacant.

25.  In the formation of metallic crystal, the ions are connected
indirectly through the free electrons surrounding them and
each atom attracts as many neighbouring atoms as it can.
 The result is closely packed structure having strong
interatomic bonds.
 Hence the metallic crystals have close packed structure with
high densities. Metallic crystals usually crystalline with
identical atoms in FCC structure.

27.  In the unit cell, each corner of the cube
contains one atom and at each face center of
the cube there is an atom.
 Thus there are eight corner atoms and six
face centered atoms.
 In this case the nearest neighbours of any
corner atom are the face centered atoms of
the surrounding unit cells.
 Any corner atom has four such atoms in its
own plane, four in a plane above it and four
in a plane below it. Thus its coordination
number is twelve.
The coordination number is 12

28. A
4r
a
H
G
F
E
D
C
B
For a FCC unit cell, the atomic radius
can be calculated from the Figure.
From the Figure, AF = 4r and AB = a
From the triangle ABF
AB2 + BF2 = AF2
a2 + a2 = (4r)2
r2 = 2a2 / 16
r = a / 2
r = a / 2
a = 2 r

29. Thus, the packing factor is 74%. When we compare with SC and BCC,
this has high packing fraction and so most of the metals like copper,
Aluminium and Silver have this structure with high density

30. Germanium, Silicon and diamond possess a structure which is a
combination of two interpenetrating FCC sub-lattices along the body
diagonal by ¼th cube edge.
Diamond is a metastable allotrope of
carbon where the each carbon atom is
bonded covalently with other surrounding
four carbon atoms and are arranged in a
variation of the face centered cubic crystal
structure called a diamond lattice

31. One sub-lattice, say ‘x’, has it origin at the point (0, 0, 0) and the
other sub-lattice y, has its origin quarter of the way along the body
diagonal i.e., at the point (a/4, a/4, a/4). The basic diamond lattice is
shown in figure.
Each atom in 2nd sub-lattice is surrounded by four atoms in 1st FCC
sub-lattice.
Then the coordination number is 4
In the unit cell, in addition to the eight corner atoms, there are six face
centred atoms and four more atoms are located inside the unit cell. Each
corner atom is shared by eight adjacent unit cells and each face centred
atom is shared by two unit cells.
Hence the total number of atoms per unit cell is 8.

32. x
y
z
p
x
z
p
y
2r
a/4
a/4
a/4
From the triangle xyp
xy2 = yp2 + px2
xy2 = (a/4)2 + (a/4)2
xy2 = 2(a/4)2
(1)
From the triangle xyz
xz2 = xy2 + yz2
(2r)2 = 2(a/4)2 + (a/4)2
4r2 = 3a2/16
r = a / 8
[Substituted eq. (1) here]

33. Thus, 34 % of the volume of the diamond unit cell is occupied by
atoms and the remaining 66 % volume of the unit cell is vacant.
Thus it is a loosely packed structure

34. Coordination Number

35.  In crystal analysis, it is essential to indicate certain directions
inside the crystal.
 Suppose we want to indicate the direction OP as shown in Fig.
 x, y and z are the crystallographic axes. If a, b and c represent unit
translational vectors along x, y and z directions, then moving u
times ‘a’ along x-axis, v times ‘b’ along y-axis and w times ‘c’
along z-axis, we can reach P. If u, v and w are the smallest integers,
the direction OP indicated by [uvw].
p

36. 36
 The crystal lattice may be regarded as made up of an infinite set of
parallel equidistant planes passing through the lattice points which
are known as lattice planes.
 In simple terms, the planes passing through lattice points are
called ‘lattice planes’.
 For a given lattice, the lattice planes can be chosen in a different
number of ways.
d
DIFFERENT LATTICE
PLANES

37. 37
 The orientation of planes or faces in a crystal can be described in
terms of their intercepts on the three axes.
 Miller introduced a system to designate a plane in a crystal.
 He introduced a set of three numbers to specify a plane in a
crystal.
 This set of three numbers is known as ‘Miller Indices’ of the
concerned plane.
Miller indices is defined as the reciprocals of the
intercepts made by the plane on the three axes.

38. 38
 Step 1: Determine the intercepts of the plane along the axes X,Y
and Z in terms of the lattice constants a, b and c.
 Step 2: Determine the reciprocals of these numbers.
 Step 3: Find the least common denominator (lcd) and multiply
each by this lcd to get the smallest whole number.
 Step 4:The result is written in paranthesis.
 This is called the `Miller Indices’ of the plane in the form (h k l).

39. 39
PLANES IN A CRYSTAL
Plane ABC has intercepts of 2 units along X-axis, 3
units along Y-axis and 2 units along Z-axis.
DETERMINATION OF
‘MILLER INDICES’
Step 1:The intercepts are 2, 3 and 2 on the
three axes.
Step 2:The reciprocals are 1/2, 1/3 and ½.
Step 3:The least common denominator is ‘6’. Multiplying
each reciprocal by lcd, we get, 3, 2 and 3.
Step 4:Hence Miller indices for the plane ABC is (3 2 3)

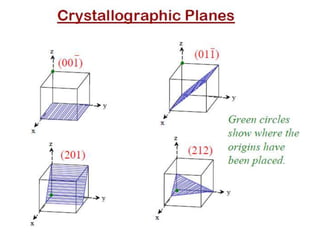
40.  When a plane is parallel to any axis, the intercept of the plane on
that axis is infinity. Hence its Miller index for that axis is zero.
 When the intercept of a plane on any axis is negative a bar is put on
the corresponding Miller index.
 All equally spaced parallel planes have the same index number
(h k l).
 If the plane passes through origin, it is defined in terms of a
parallel plane having non-zero intercept.
 If a normal is drawn to a plane (h k l), the direction of the normal is
[h k l]

41. 41
EXAMPLE
( 1 0 0 ) plane
Plane parallel to Y and Z axes

42. 42
EXAMPLE
In the above plane, the intercept along X axis is 1 unit.
The plane is parallel to Y and Z axes. So, the intercepts
along Y and Z axes are ‘’.
Now the intercepts are 1,  and .
The reciprocals of the intercepts are = 1/1, 1/ and 1/.
Therefore the Miller indices for the above plane is (1 0 0).

43. 43
MILLER INDICES
IMPORTANT FEATURES OF MILLER INDICES
A plane passing through the origin is defined in terms of a
parallel plane having non zero intercepts.
All equally spaced parallel planes have same ‘Miller
indices’ i.e. The Miller indices do not only define a particular
plane but also a set of parallel planes. Thus the planes
whose intercepts are 1, 1,1; 2,2,2; -3,-3,-3 etc., are all
represented by the same set of Miller indices.
This slide is only for understanding

44. 44
MILLER INDICES
IMPORTANT FEATURES OF MILLER INDICES
It is only the ratio of the indices which is important in this
notation. The (6 2 2) planes are the same as (3 1 1) planes.
If a plane cuts an axis on the negative side of the origin,
corresponding index is negative. It is represented by a bar,
like (1 0 0). i.e. Miller indices (1 0 0) indicates that the
plane has an intercept in the –ve X –axis.
This slide is only for understanding

45. Z
X
O
Cˡ
Bˡ
Aˡ
C
B
A
Y
M
N
If (h k l) is the Miller indices of a crystal plane ABC, then the
intercepts made by the plane with the crystallographic axes are given as
where a, b and c are the primitives.
a b c
, and
h k l

46. Consider a cubic crystal of side ‘a’, and a plane ABC.
This plane belongs to a family of planes whose Miller indices
are (h k l) because Miller indices represent a set of planes.
Let ON =d1, be the perpendicular distance of the plane ABC
from the origin.
Let ʹ, ʹ and ʹ (different from the interfacial angles,  and )
be the angles between co-ordinate axes X, Y, Z and ON
respectively.
The intercepts of the plane on the three axes are,
a a a
OA , OB and OC
h k l
   (1)

47. 47
From the figure, we have,
(2)
From the property of direction of cosines,
(3)
1 1 1
1 1 1
d d d
cos ,cos and cos
OA OB OC
     
2 1 2 1 2 1
cos cos cos 1
     

48. PH 0101 UNIT 4 LECTURE 2 48
Using equation 1 in 2, we get,
(4)
Substituting equation (4) in (3), we get,
1 1 1
1 1 1
d h d k d l
cos ,cos , and cos
a a a
     
2 2 2
1 1 1
d h d k d l
1
a a a
     
  
     
     
2 2 2
2 2 2
1 1 1
2 2 2
d h d k d l
1
a a a
  

49. PH 0101 UNIT 4 LECTURE 2 49
i.e.
(5)
i.e. the perpendicular distance between the origin
and the 1st plane ABC is,
2
2 2 2
1
2
d
(h k l ) 1
a
  
2
2
1 2 2 2
a
d
(h k l )

 
1
2 2 2
a
d ON
h k l
 
 
1
2 2 2
a
d
h k l

 

50. PH 0101 UNIT 4 LECTURE 2 50
Now, let us consider the next parallel plane AʹBʹCʹ
Let OM=d2 be the perpendicular distance of this
plane from the origin.
The intercepts of this plane along the three axes are
1 1 1
2a 2a 2a
OA ,OB ,OC ,
h k l
  
2
2 2 2
2a
OM d
h k l
  
 

51. 51
• Therefore, the interplanar spacing between two
adjacent parallel planes of Miller indices (h k l ) is
given by, NM = OM – ON
i.e.Interplanar spacing
(6)
 
2 1
2 2 2
a
d d d
h k l
  
 

52. 52
MILLER INDICES OF SOME IMPORTANT PLANES

54. X
Z
Y

56.  Find intercepts along axes → 2 3 1
 Take reciprocal → 1/2 1/3 1
 Convert to smallest integers in the same ratio → 3 2 6
 Enclose in parenthesis → (326)
(2,0,0)
(0,3,0)
(0,0,1)
Miller Indices for planes

57. Intercepts → 1  
Plane → (100)
Family → {100} → 6
Intercepts → 1 1 
Plane → (110)
Family → {110} → 6
Intercepts → 1 1 1
Plane → (111)
Family → {111} → 8
(Octahedral plane)
Cubic lattice
X
Y
Z

61. [010]
[100]
[001]
[110]
[101]
[011]
[110] [111]
Procedure as before:
• (Coordinates of the final point  coordinates of the initial point)
• Reduce to smallest integer values
Important directions in 3D represented by Miller Indices (cubic lattice)
Face diagonal
Body diagonal
X
Y
Z
Memorize these

64. 64
Worked Example
The lattice constant for a unit cell of aluminum is 4.031Å Calculate
the interplanar space of (2 1 1) plane.
a = 4.031 Å
(h k l) = (2 1 1)
Interplanar spacing
 d = 1.6456 Å
PROBLEMS
10
2 2 2 2 2 2
4.031 10
a
d
h k l 2 1 1


 
   