pH, BUFFERS & ISOTONIC SOLUTIONS.pptx

pH, BUFFERS & ISOTONIC
SOLUTIONS
BALASUNDARESAN M

Contents
1. Sorensen’s pH scale
2. pH determination (electrometric and calorimetric)
3. Buffer equation
4. Buffer capacity
5. Buffers in pharmaceutical and biological systems
6. Applications of buffers
7. Buffered isotonic solutions.
2

Definitions
🠶 pH is a measure of how acidic/basic water is. The range goes from 0 - 14, with 7 being neutral. pHs of less than 7
indicate acidity, whereas a pH of greater than 7 indicates a base . (Or) pH is really a measure of the relative amount
of free hydrogen and hydroxyl ions in the water
🠶 Buffer: “Buffers are compounds or mixtures of compounds that by their presence in the solution resist changes in
the pH upon the addition of small quantities of acid or alkali.”
🠶 Buffer Action: The resistance of a buffer solution to a change in pH isknown as buffer action.
🠶 Buffer Capacity: It is defined as the ratio of the increment of strong base (or acid) to the small change in pH brought
about by this addition . The buffer capacity is expressed as the amount of strong acid or base, in gram-equivalents,
that must be added to 1 liter of the solution to change its pH by one unit.
🠶 Isotonic: These are the solutions which produce the same osmotic pressure as that of the cell contents in question,
without net gain or loss of water by both solutions, provided the cell membrane isimpermeable to solutes.
🠶 Tonicity: Tonicity is a measure of the effective osmotic pressure gradient , as defined by the water potential of two
solutions separated by a semipermeable membrane
3

Sorensen’s pH Scale
🠶 The concept of pH scale was first introduced by Danish chemist Soren
Peder Lauritz Sorensen (S.P.L. Sorensen), in the year 1909. The scale
was later revised to the modern pH in the year 1924.
🠶 Sorenson defined pH as the logarithm of the reciprocal of hydrogen
ion concentration
(Or, it can be rearranged as)
Thus, pH may be defined as negative logarithm of hydrogen ion concentration
pH is a term used to specify the acidity or basicity of an solution . A pH scale
helps in measuring how acidic or basic a substance .
5

Sorensen’s pH Scale….
🠶 Based on the pH values and different concentrations of H+ ions, a scale has been
devised and named after Sorensen.
🠶 The scale starts with zero pH, i.e, hydrogen ion
concentration is 100. It means the solution is strongly
acidic .
🠶 At the other end of the scale, pH is 14. i.e, hydrogen
ion concentration is 10-14. It means the solution is
strongly alkaline .
🠶 The central point pH in the scale is 7.0, because [H+] is
equal to [OH+], i.e., hydrogen ion concentration is10-
7
🠶 Solutions with a pH less than 7 are acidic and solutions with a pH greater than 7
are basic. Pure water neutral, being neither an acid nor a base.
🠶 pH Applications: Enhancing solubility, Increasing stability, improving purity, Optimizing
biological activity and storage of products.
6

2. pH determination
(electrometric and calorimetric)
8

a. Calorimetric method of determination of pH
Principle:
🠶 Colorimetric means to measure color.
🠶 Colourimetric method is used to determine the pH of the solution upto ±0.2 units in
the range of pH 3 to 11.0, based on the colour changes.
🠶 The principle involves the comparison of colour of the test solution with that of the
standard solutions of definite pH values.
🠶 Several standard solutions are available commercially, which are pre-
mixed
solutions of buffer and indicator.
🠶 Capillators and comparators are available commercially.
🠶 Capillators: The buffer solutions and universal indicator are mixed and placed in
capillary tubes. A set of such standard solutions is known as capillators. These are
used for small volumes.
🠶 Comparators: For large volumes , comparators are used. These are similar to
capillators , but test tubes are used inste ad of capillary tubes. These are particularly
useful for examining turbid or coloured solutions. The test sample is also mixed with
the universal indicator. The colour produced is compared with the standard colour
of the capillators or comparators.
9

a. Calorimetric method of determination of pH. .
Method:
1. Standard buffer solutions of known pH values ranging from 3.0 to 11.0 are prepared
with 1.0 pH intervals.
2. A few drops of the universal indicator are added to each buffer solution. Different
colours are produced .
3. A few drops of universal indicator are added to the test solution so that it also
possesses the colour depending on its pH.
4. The colour of the unknown (test) solution is matched with the standard colours
produced by buffer solution. The pH of the test solution must be same as that of the
buffer, which has the same colour shade.
5. Based on the approximate pH value obtained in step (4), the pH interval is reduced
to a narrow range. For example, if the approximate pH is identified as 5, then
standard buffer solutions are prepared from pH 4 to 6 with 0.2 pH intervals.
6. Steps from (2) to (4) are repeated to obtain the actual pH of the test solution; The
exact pH of the test solution is reported .
10

a. Calorimetric method of determination of pH. .
Advantages
🠶 Colourimetic method isless expensive.
🠶 It is useful for the study of acid -base reactions in non-aqueous solution.
Disadvantages
🠶 Colourimetric method isless accurate and less convenient.
🠶 It is particularly used when the solution is not coloured or not turbid.
🠶 Since indicators themselves are acids (or bases), their addition to unbuffered
solution (whose pH is to be determined) changes the pH of the solution.
11

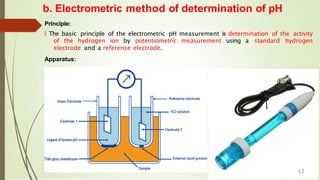
b. Electrometric method of determination of pH
Principle:
🠶 The basic principle of the electrometric pH measurement is determination of the activity
of the hydrogen ion by potentiometric measurement using a standard hydrogen
electrode and a reference electrode.
Apparatus:
12

b. Electrometric method of determination of pH..
Method:
🠶 Before use, remove electrode from storage solution, rinse, and blot, dry with a soft tissue
paper.
🠶 Calibrate the instrument with standard buffer solution. [Ex: pH 4.0, 7.0 and 10]
🠶 Once the instrument is calibrated remove the electrode from standard solution; rinse,
blot and dry.
🠶 Dip the electrode in the sample whose pH has to be measured.
🠶 Stir the sample to ensure homogeneity.
🠶 Note down the reading (pH) from the pH meter.
Advantages
• Sensitivity of the electrometric method is high. Hence, accurate measurements can be
obtained.
• The solution is uncontaminated , because the addition of indicators is avoided.
• The pH range of measurement islarge.
Disadvantages
• Electrometric method isnot suitable for viscous solutions and gels, because of poor ionic
mobility.
• Initial cost of pH meter is high compared to the colourimetric method.
13

5. buffers in pharmaceutical and
biological systems
14

I. In biological systems
a. Blood
🠶Blood consists of primary and secondary bufferssystems contributing the pH 7.4.
🠶When the pH of the blood goes below 7.0 or above 7.8, life is in danger.
🠶The pH of the blood in diabetic coma is reported to drop as low as 6.8.
It is maintained at about 7.4 by two buffer systems. That are;
Primary buffers : These are present in plasma .
The plasma contains; carbonic acid/carbonate & acid/alkali sodium salt of phosphoric acid.
Secondary buffers: these are present in erythrocytes which are;
oxy-haemoglobin / haemoglobin & acid / alkali potassium salts of phosphoric acid.
15

b. Lacrimal fluid (pH 7.4, in range of 7-
8 or slightly )
Lacrimal fluids (or tears) have been found to have a great degree of buffer
capacity ,allowing dilution of 1:15 with neutral distilled water. The pH of tears is
about 7.4, with a range of 7.0 to 8.0.
c. Urine
🠶 pH: 6.0 (range 4.5 – 7.8)
🠶 below normal…hydrogen ions are excreted by the kidney.
🠶 above pH 7.4…hydrogen ions are retained by action of the kidney.
I. In biological systems....
16

🠶 Buffers are widely used in the field of pharmacy as ingredients in most of the
pharmaceutical formulations in order to adjust the pH of the product to that
required for maximum stability.
a. In parenteral preparations (i.e. injections)
🠶 In case of parenteral preparations, pH should be considered carefully as large
deviations of pH may lead to serious consequences. The ideal pH of a
parenteral product is 7.4, which is pH of blood. The most commonly used buffers
in parenteral products (injections) are acetate, phosphate, citrate and
glutamate .
II. In pharmaceutical systems
17

b. In ophthalmic preparations (i.e. eye preparations)
🠶 Buffers are generally used in ophthalmic preparations to maintain the pH within the
physiological pH range of lacrimal fluid (i.e. eye fluid). The lacrimal fluid has a pH in
rang 7 – 8 (7.4), but it has good buffering capacity and can tolerate preparations
having pH values between 3.5 – 10.5 with little discomfort. Out side this range (i.e. 3.5
below and 10.5 above), increase lacrimation (the flow of tears) may occur with
other complications .
🠶 The buffering agents most commonly used in ophthalmic preparations include
borate, carbonate and phosphates.
c. In ointments and creams
🠶 Topical products (which are used on skins) such as ointments and creams are also
buffered to ensure stability of the formulation. The most commonly used buffers in
ointments and creams are citric acid / its salts & phosphoric acid / its salts.
18

Factors influencing pH of buffer
⚫ Addition of small amt of water cause small +ve or –ve deviation bcz it alters activity
coefficient and water itself behave as a weak acid or weak base.
⚫ +ve value of dilution :pH rises with dilution
⚫ -
ve value of dilution :pH falls with dilution.
Temperature :
⚫ The pH values in the current use are based on the studies at 25 oC
⚫ Asthe temp. increases:
Acetate buffers: pH increase
Boric acid- sodium borate buffers: pH decrease
19

Ionic strength/SALT EFFECT
:
🠶 Addition of neutral salt to buffer solution changes the pH of the solution due to altered
ionic strength.
🠶 Dilution of buffers also changes the pH due to altered ionic strength.
🠶 Therefore, whenever pH of buffer solution is mentioned, ionic strength should also be
specified.
Factors influencing pH of buffer…
20

⚫ Select a weak acid having a pKa near to a pH at which the buffer is to be used to ensure a
max buffer capacity.
⚫ Calculate the ratio of salt and weak acid required to obtain the desired pH. The buffer eqn is
satisfactory for approximate calculation within the pH range of 4 to 10.
⚫ Consider the individual concentration of the buffer salt and acid needed to obtain a
suitable buffer capacity.
⚫ A conc of 0.05 to 0.5M is usually sufficient and buffer capacity of 0.01 to 0.1 is generally
adequate.
Steps to develop a new buffer solution.
21

🠶 Availability of chemicals, sterility of the final solution, stabilty of the drug and buffer on aging,
cost of materials, and freedom from toxicity should be considered.
🠶 E.g. a borate buffer, bcz of its toxic effects, certainly can not be used stabilize a solution to
be administered orally or parenterally.
🠶 Determine the pH and buffer capacity of the completed buffered solution using a reliable pH
meter.
🠶 When the electrolyte conc ishigh, the pH calculated by use of the buffer eqn issomewhat
different from the experimental value.
🠶 It is to be expected when activity coefficient are not taken in to account .
Steps to develop a new buffer solution...
22

Pharmaceutical Buffers
⚫ The buffers of clark and Lubs were determined at 20 o C and re- determined at 25 o C.
⚫ The mix and their ph ranges are:
⚫ 1. HCl and KCl, 1.2 to 2.2.
⚫ 2. HCl and KHP, 2.2. to 4.0
⚫ 3. NaOH and KHP, 4.2 to 5.8
⚫ 4. NaOH and KH2PO4, 5.8 to 8
⚫ 5. H3BO3, NaOH, and KCl, 8 to 10.
⚫ Below pH 2 HCl alone has considerable buffer efficiency and KCl isneutral salt and is added
to adjust the ionic strength.
23

6. APPLICATIONS OFBUFFERS
The applications remain same for pH and buffer solutions, because
buffers are used for maintaining a definite pH of the solution.
24

a. Enhancing solubility
🠶 If pH of a solution is not adjusted properly, drug present in the solution may
precipitate . This principle is applied in the manufacture of dosage forms.
🠶 For example, sodium salicylate precipitates as salicylic acid, when
acidified . Therefore, optimum pH should be adjusted for maximum solubility.
🠶 Acidic drugs are more soluble in alkaline pH due to in situ formation of salt.
The pH is maintained by choosing a suitable buffer. Similarly, basic drugs
are more soluble in acidic solutions, because they are predominantly in
ionic form, which ismore soluble in water (aqueous media).
25

b. Increasing stability
🠶 Many drugs get hydrolysed in aqueous solutions. Adjusting the pH of the
solution stabilizes such drugs.
🠶 For example, vitamins are stable only within a narrow range of pH. Suitable
buffer isselected for optimum stability.
26

c. Improving purity
🠶 Proteins are purified based on the fact that amphoteric compounds are
least soluble at their isoelectric points. The isoelectric pH is maintained using
suitable buffer.
🠶 For example, insulin precipitates from aqueous solutions at pH 5.0 to 6.0. This
method isused for the purification of insulin.
•Amphoteric compound: Able to react both as a base and as an acid.
•The isoelectric point is the pH at which a particular molecule carries no net electrical charge.
27

d. Optimizing biological activity
🠶 Enzymes have maximum activity at definite pH values. Hence buffer of
desired pH is added to the preparation.
🠶 For example, pepsin has maximum activity at pH 1.5.
28

e. Comforting the body
🠶 Some of the solutions when applied to tissues cause irritation, if their pH is greatly
different from normal pH of the relevant body fluids.
🠶 Therefore, while formulating the solutions meant for applying to the sensitive body
parts, such as eyes (irritation), blood (hemolysis ) and abraded skin surfaces (burning
sensation) the pH of the preparation must match with the pH of the physiological
fluids.
29

7. Buffered Isotonic solutions
30

Introduction
🠶 Isotonic buffered solution is defined as a solution which maintains the
isotonicity and the pH as that of the body fluids.
⚫ Isotonic solutions cause no swelling or contraction . E.g. isotonic NaCl solutions.
Isotonic:
These are the solutions which produce the same osmotic pressure as that of
the cell contents in question, without net gain or loss of water by both solutions,
provided the cell membrane is impermeable to solutes.
31

a. Isotonic Solutions
These are the solutions which produce the same osmotic pressure as that of
the cell contents in question, without net gain or loss of water by both
solutions, provided the cell membrane is impermeable to solutes.
⚫ Ex: 0.9 % w/v saline (NaCl) solution
⚫ Blood cells +0.9 % NaCl = cells retain normal size (Isotonic with blood)
32

b. Hypertonic Solutions
These are defined as the solutions containing the solute in higher
concentration than that isrequired for isotonic solutions
⚫ Ex: 2 % w/v saline (NaCl) solution (concentration >0.9 w/v)
⚫ Blood cells +2 % NaCl =cells shrink and become wrinkled (Hypertonic with
blood)
33

lower
c. Hypotonic Solutions
These are defined as the solutions containing the solute in
concentration than that isrequired for isotonic solutions
⚫ Ex: 0.2 % w/v saline (NaCl) solution (concentration <0.9 w/v)
⚫ Blood cells +0.2 % NaCl = cells swells and burst liberating hemoglobin
(Hypotonic with blood)
34

Measurement of Tonicity
🠶A part from Nacl a no. of drugs and chemicals are used in
formulations which also contribute to tonicity of solution. There
methods are need to measure tonicity and to adjust the tonicity.
🠶 Two methods
A. Hemolytic method
B. Cryoscopic method or depression of freezing point
35

Measurement of Tonicity….
A. Hemolytic Method
🠶 Red blood cells are suspended in various solutions and the appearance of RBCs is observed for swelling,
bursting, shrinking and wrinkling of the blood cells.
• In hypotonic solutions, oxyhemoglobin is
released, which is in direct proportion to the
number of cells hemolysed.
• In hypertonic solutions, the cells shrink and
become wrinkled or crenated (notched
surface)
• In isotonic solutions, the cells do not change
their morphology.
36

HYPERTONIC ISOTONIC HYPOTONIC
NaCl 2% NaCl 0.9% NaCl 0.2%
solute ‹ solute Inside
outside
solute =solute Inside
outside
solute › solute Inside
outside
SHRINKAGE EQUILIBRIUM SWELLING
37

Measurement of Tonicity…
B. Cryoscopic method or depression of freezing point
 Colligative properties of solutions are helpful in determining the isotonicity values.
 Among them, depression of freezing point is extensively used.
 Water has a freezing point of 0OC. When substance such as Nacl are added to water, the freezing
point of water decreases .
 Such as a solution shows same osmotic pressure as that of the blood . Hence, the functions of RBC
and tissues do not alter.
∆Tf= -0.52 ºC (Freezing point depression of human blood & lacrimal fluid)
T
he depression of freezing point ( ∆Tf) of blood is -0.52 ºC . Therefore, the ∆Tf value of
the drug solution should also be -0.52 ºC .
38

🠶 Since osmotic pressure of a solution is not a readily measurable quantity, other easily
measurable colligative properties such as the freezing point depression are used in the
isotonicity calculations .
🠶 Isotonicity value is defined as the concentration of an aqueous Nacl solution having
same colligative properties (freezing point, boiling point, vapor pressure and osmotic
pressure)as the solution in question.
🠶 Class I methods: These methods involve addition of Sodium Chloride (or another substance) to
lower the freezing point of soln. to -0.52° C
A. Cryoscopic Method
B. Sodium Chloride Equivalent method
🠶 Class II methods: These methods involve addition of water to form an isotonic solution.
C. Sprowls method
D. White Vincent method
Methods for adjustment of Tonicity
39

A. Cryoscopic Method:
🠶 Pure water has a freezing point (Tf) of 0°C. When solutes are added to water, its
freezing point is lowered.
🠶 Blood plasma has a freezing point of −0.52 because of acids, salts and
Haemoglobin .
🠶 0.9% sodium chloride has the same osmotic pressure and the same freezing
point depression of -0.52 as that of blood plasma, red blood cells, and tears.
🠶 Drug solutions which have a freezing point depression of -
0.52 are, therefore,
isotonic with blood.
Methods for adjustment of Tonicity…
Solution (1% w/v drug) ∆ Tf,
oC E
Apomorphine Hcl -0.08 0.14
Boric acid -0.29 0.50
Calcium gluconate -0.09 0.16
Pilocarpine nitrate -0.14 0.23
Potassium chloride -0.45 0.76
Sodium chloride -0.58 1.00
Sodium sulphacetamide -0.14 0.23
W= weight in grams of the adjusting substance per 100 ml.
a= Freezing point depression of 1 % solution of pure drug.
b= Freezing point depression of 1 % solution of adjusting substance.
40

B.Sodium Chloride Equivalent Method:
🠶 Sodium Chloride Equivalent (E) of a drug is the Amount of NaCl that is equivalent
to(i.e., has the same osmotic effect (same f.p.d) as) 1 gm of drug.
🠶 For example, potassium chloride has sodium chloride equivalent (E) value of 0.76 gm
NaCI / gm of KCI-. This means 0.76 gm of NaCI produce the same osmotic effect as 1
gm of KCI
🠶 The Nacl equivalents of a number of drugs and other ingredients are given in table . In
the absence of the data, the E value of a new drug can be calculated from the below
equation.
Methods for adjustment of Tonicity….
Where, M= Molecular weight, gram/Mole
Liso=Freezing point depression of the drug solution for showing isotonicity
•To make a solution of a particular drug isotonic with blood plasma, the sodium choride
equivalent value (E) of that drug is noted from the reference table or calculated
•Amount of NaCI required =0.9% -{% of solution x E)
41

Find the amount of sodium chloride needed to make a -
solution of 0.5% of KCI isotonic with blood plasma .
Sodium chloride equivalent value (E) of KCI is 0.76.
🠶Given solution (not isotonic) =0.5% KCI
🠶 E value of KCI =0.76 So, by applying formula,
🠶Amount of NaCI required =0.9 -(% of drug x E)
🠶=0.9-
(0.5 x0.76)
🠶=0.9 -
0.38 =0.52 gm
🠶Hence, 0.52 gm of NaCI must be added in
0.5% KCI solution to make it isotonic.
42

Methods for adjustment of Tonicity…..
C. White Vincent Method:
🠶 1st Addition of H2O to drug to make it isotonic
🠶 2nd addition of isotonic vehicle to bring solution to final volume
This method involves the addition of water to the given amount of drug to make isotonic
solution, followed by the addition of some other isotonic solution (e.g. 0.9% NaCI) to make the
final volume.
The volume of water that should be added in given amount of drug to make isotonic
solution is calculated by using following formula;
V = W x Ex 111.1
Where, V =volume of water needed to make isotonic solution
W =given weight of drug in grams
E =NaCI equivalent value of drug
111.1 =constant
43

D. Sprowls Method:
🠶 1st Addition of H2O to drug to make it isotonic
🠶 2nd addition of isotonic vehicle to bring solution to final volume
 The Sprowls method, a modified method of the White–Vincent method, calculates the isotonic
volume by using fixed mass of the material. This method involves the addition of water to the given
amount of drug to make isotonic solution, followed by the addition of some other isotonic solution (e.g.
0.9% NaCI) to make the final volume.
The volume of water that should be added in given amount of drug to make isotonic solution is
calculated by using following formula;
V = 0.3 x Ex 111.1
Where, V =volume of water needed to make isotonic solution
0
…
3 = weight of drug in grams (Constant)
E =NaCI equivalent value of drug
111.1 =constant
45

3. BUFFEREQUATION
(Henderson – Hasselbalch equation)
46

For Acid Buffers:
T
he pH of acid buffer can be calculated
dissociation constant, Ka of the weak acid
from the
and the
concentrations of the acid and salt used.
🠶T
he dissociation expression of the weak acid can be
represented as:
🠶HA ↔ H+ + A-
🠶Ka =[H+] [A-
] / [HA]
🠶Or
🠶[H+] = Ka [HA] / [A-] -
-
-
-
-
-
-
-
-
-
-
-
- (1)
47

🠶 A weak acid is only slightly dissociated, and its dissociation is
further depressed by the addition of the salt (XA) which provides
‘A-’ ion (common ion effect) as a result the equilibrium
concentration of the unionized acid is nearly equal to the initial
concentration of the acid.
🠶 The equilibrium concentration of ‘A-’ is assumed to be equal to
the initial concentration of the salt added since it is completely
dissociated.
🠶 Therefore, in above equation (1), we represent concentration of
‘A-’ by salt concentration.
48

🠶 [H+] = Ka. [Acid] / [Salt] --------- (2)
🠶 Taking log on both sides, we get:
🠶 log[H+] = logKa + log [Acid] / [Salt]
🠶 multiplying both sides by –ve sign,
🠶 -log[H+] = -logKa - log [Acid] / [Salt]
🠶 As -log[H+] = pH & -logKa = pka
🠶 pH = pka - log[Acid] / [Salt] OR
pH = pka + log[Salt] / [Acid] ---------- (3)
Eq. (3) is called as Henderson – Hasselbalch equation.
It helps in calculating the pH value of buffer solution,
if the concentrations of acid as well as that of the salt are known.
49

For Basic Buffers
Buffer equation for basic buffer can be calculated in same way as that
for acidic buffers.
Consider a basic buffer composed of a mixture of weak base (BOH)
and its salt (BA). The dissociation constant for base can be written as,
BOH ↔ B+ + OH-
Kb = [B+] [OH-] / [BOH]
OR
[OH-] = Kb [BOH] / [B+] ------------- (1) 50

🠶A weak base is only slightly dissociated, and its dissociation is
further depressed by the addition of the salt (BA) which provides
B+ ion (common ion effect) as a result the equilibrium
concentration of the unionized base is nearly equal to the initial
concentration of the base.
🠶 The equilibrium concentration of B+ is assumed to be equal to
the initial concentration of the salt added since it is completely
dissociated.
🠶 Therefore, in above equation (1), we represent concentration of
B+ by salt concentration.
51

[OH-] = Kb. [Base] / [Salt] --------- (2)
Taking log on both sides, we get:
log[OH-] = logKb + log [Base] / [Salt]
multiplying both sides by –ve sign,
-log[OH-] = -logKb - log [Base] / [Salt]
As -log[OH-] = pOH & -logKb = pkb
pOH = pkb – log [Base] / [Salt]
Or
pOH = pkb + log[Salt] / [Base] ---------- (3)
52

Significance of Henderson – Hasselbalch equation:
By this equation, the pH of a buffer solution can be calculated from the initial
concentrations of the weak acid and the salt provided when ka is given.
However, the Henderson equation for a basic buffer will give pOH, and so pH
can be calculated as;
pkw = pH + pOH
or pH = pkw – pOH
pH = 14 – PoH
Also, the dissociation constant of a weak acid (pka) or a weak base (pkb) can
be calculated by measuring the pH of a buffer solution containing equimolar
concentrations of the acid (or base) and the salt.
53

Applications Henderson–Hasselbalch
equation.
🠶 Applications:
1. For definite pH solution, it isessential to add salt and acid (or base) to water in a
desired ratio. This ratio is determined by Henderson–Hasselbalch equation.
2. Since salt and acid are added in preparation of buffer solutions, their
concentrations are known. Hence using this data, the resultant pH of a solution can
be calculated using Henderson–Hasselbalch equation.
3. The pKa of various drugs can be determined from pH of solutions.
4. A suitable salt forming substance can be selected based on Henderson–
Hasselbalch equation.
5. The solubility of a substance at any pH can be predicted provided intrinsic
solubility (Si) and pKa are known
54

BUFFER CAPACITY
🠶 The buffer capacity of a buffer solution is “a measure of its magnitude of its
resistance to change in the pH on an addition of an acid or a base.”
🠶 The magnitude of the resistance of a buffer to pH changes is referred to as the
buffer capacity, β.
🠶 Buffer capacity is also referred as buffer index, buffer value, buffer efficiency or
buffer coefficient.
🠶 The buffer capacity represented by ‘β’ may also be defined as:
🠶 “The ratio of the increment (amount added) of strong acid or base to the small
change in pH (ΔpH) brought about by this addition”.
🠶 β =ΔA or ΔB / ΔpH
🠶
🠶 Where, ΔA or ΔB represents the small increment (in gram equivalents / litre of
strong acid or base added) to the buffer to bring about a pH change of ΔpH.
56

🠶 According to the above equation, a solution has a buffer capacity of 1
when one litre of it requires one gram equivalent of a strong acid or base to
change the pH by one unit. So, smaller the pH change in a solution upon
the addition of an acid or base, greater is the buffer capacity and vice
versa.
57

Types of buffers:
Generally buffers are of two types;
🠶Acidic buffers
🠶Basic buffers
58

Acidic Buffers:
An acidic buffer is a combination of weak acid
and its salt with a strong base.
i.e. Weak acid & salt with strong base
(conjugate base).
EXAMPLES:
🠶CH3COOH / CH3COONa
🠶H2CO3 / NaHCO3
🠶H3PO4 / NaH2PO4
🠶HCOOH / HCOONa
59

Basic Buffers:
A basic buffer is a combination of weak base and its
salt with a strong acid.
i.e. Weak base & salt with strong acid (conjugate
acid).
EXAMPLES:
🠶NH4OH / NH4Cl
🠶NH3 / NH4Cl
🠶NH3 / (NH4)2CO3
60

Buffer action
🠶The resistance of a buffer solution to a change in
pH is known as buffer action.
61

Necessity of a buffer system:
🠶 Sometimes it is necessary that a solution of a definite pH be prepared and
stored.
🠶 The preservation of such a solution is even more difficult than its
preparation. If solution comes in contact with air, it will absorb CO2 and
becomes acidic.
🠶 On the other hand, if solution is stored in a glass bottle, alkaline impurities
from the glass may alter its pH.
🠶 Due to these reasons, pharmaceutical solutions are buffered as the buffer
solutions are capable of maintaining pH at some fairly constant value
when even small amounts of acid or base are added .
62

Phosphate Buffers (Double salt buffers):
Besides the two general types of buffers (i.e.
acidic & basic), a third appears to exist. This is
buffer system composed of two salts:
Monobasic potassium phosphate (KH2PO4)
Dibasic potassium phosphate (K2HPO4).
63

pH, BUFFERS & ISOTONIC SOLUTIONS.pptx

More Related Content

What's hot

Similar to pH, BUFFERS & ISOTONIC SOLUTIONS.pptx

More from BALASUNDARESAN M

Recently uploaded

pH, BUFFERS & ISOTONIC SOLUTIONS.pptx