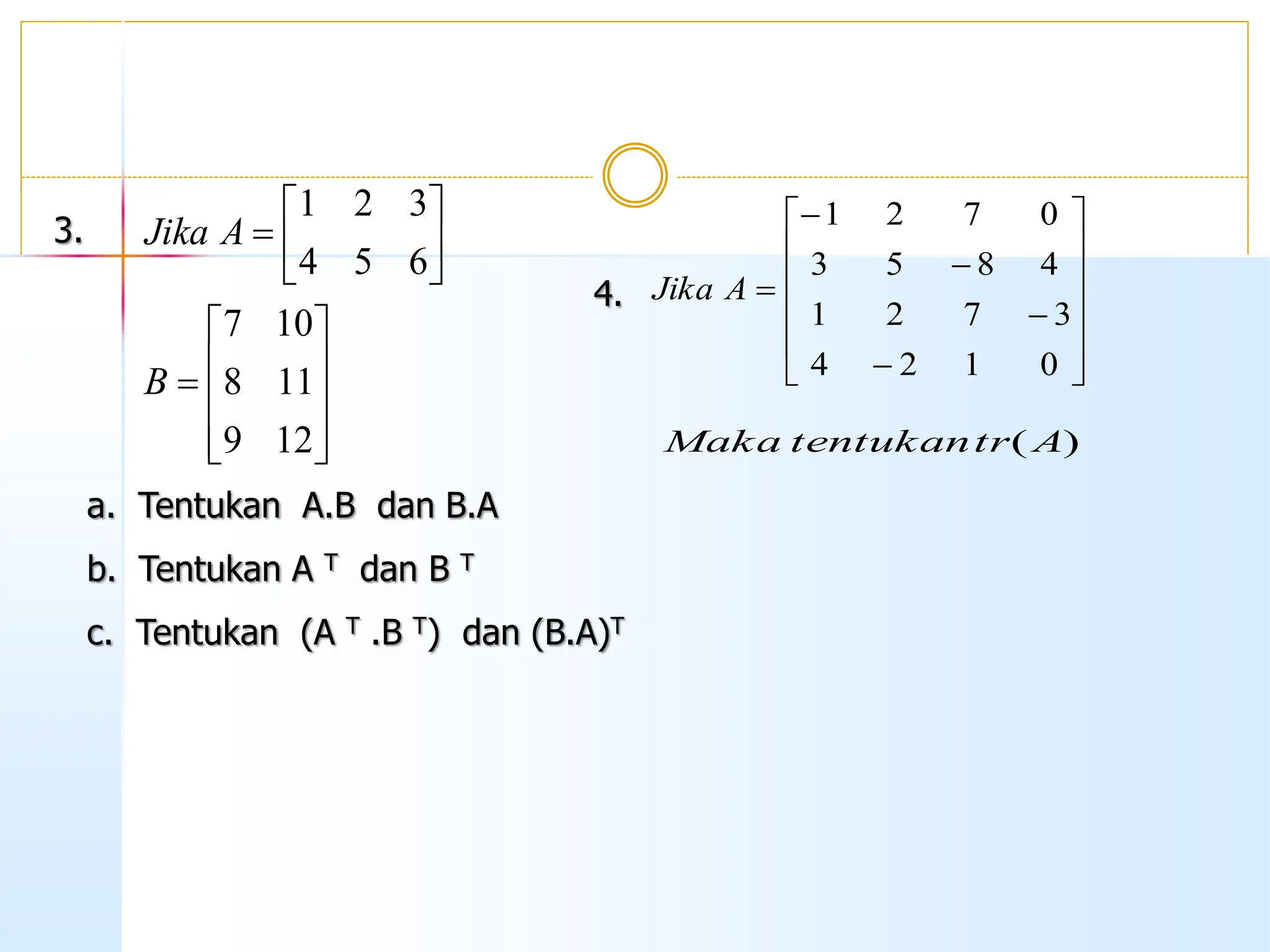
Dokumen ini membahas tentang matriks dan operasi-operasinya termasuk penjumlahan, pengurangan, perkalian, dan transpos matriks. Selain itu, disebutkan syarat-syarat untuk melakukan operasi tersebut serta sifat-sifat yang berlaku pada operasi matriks. Terdapat juga contoh-contoh untuk memperjelas setiap operasi yang dijelaskan.

1. MATRIKS DAN OPERASINYA
PERTEMUAN 2

2. Matriks Baris dan Kolom
Matriks Kolom
Matriks Baris
 
14
13
12
11
a
a
a
a matriks orde 1x4
matriks orde 3x1










31
21
11
a
a
a

3. Penjumlahan dan Pengurangan Matriks
 Misalkan A = [ aij] dan B = [bij]
Penjumlahan /Pengurangan Matriks A dan B
dinyatakan
 C = A +B atau C = A - B
Syarat Dimensi A + Dimensi B
 Aturan : Cij = Aij+Bij atau Cij = Aij - Bij
Kedua Matriks harus berorde sama.
Penjumlahan dan pengurangan dilakukan terhadap elemen-
elemen yang berkorespons

4. Penjumlahan Matriks
=
=
4 2 3
5 7 6
+
1 7 9
3 6 -2
4+1 2+7 3+9
5+3 7+6 6+(-2)
5 9 12
8 13 4

5. Pengurangan Matriks
=
=
4 2 3
5 7 6
_
1 7 9
3 6 -2
4-1 2-7 3-9
5-3 7-6 6-(-2)
3 -5 -6
2 1 8

6. Perkalian Dua Matriks
 Syarat perkalian dua buah matriks
 Misalkan C = A . B
 Banyak kolom A = Banyak Baris B
k
n
J j
b
a
C 

 1
)
(
k
ke
kolom
pada
b
elemen
dengan
j
ke
baris
pada
a
elemen
antara
perkalian
semua
dari
jumlah



7. Perkalian Matriks
Perkalian Skalar
Mengalikan suatu matriks dengan bilangan tunggal (yaitu bilangan skalar)
: dengan mengalikan elemen matriks dengan bilangan itu
4 x
Berarti faktor persekutuan setiap elemen juga dapat dikeluarkan sehingga :
3 2 5
6 2 7
2 3 9
=
12 8 20
24 8 28
8 12 36
10 25 45
35 15 50
40 -5 30
2 5 9
7 3 10
8 -1 6
= 5 x

8. Perkalian Dua Matriks
Dua buah matriks dapat dikalikan apabila
jumlah kolom matriks pertama = jumlah baris matriks kedua
Maka a.b =
a11 a12 a13 a14
a21 a22 a23 a24
a31 a32 a33 a34
b1
b2
b3
b4
.
a11b1 + a12b2 + a13b3 + a14b4
a21b1 + a22b2 + a23b3 + a24b4
a31b1 + a32b2 + a33b3 + a34b4
=

9. Contoh Perkalian Dua Matriks
4x8 + 7x5 + 6x9
2x8 + 3x5 + 1x9
=
121
40
=
4 7 6
2 3 1
8
5
9
.

10. Contoh Perkalian Dua Matriks
Jika :
Maka A.B :
Perhatikan : perkalian Matriks 3x2 dengan matriks 2x4 menjadi matriks 3x4
1 5
2 7
3 4
A =
8 4 3 1
2 5 8 6
dan B =
1x8 +5x2 1x4+5x5 1x3+5x8 1x1+5x6
2x8 +7x2 2x4+7x5 2x3+7x8 2x1+7x6
3x8 +4x2 3x4+4x5 3x3+4x8 3x1+4x6
18 29 43 31
30 43 62 44
32 32 41 27

11. Perkalian Dua Matriks
Jika A (orde mxn) dengan B (orde nxm),
apakah A.B = B.A ?

12. SIFAT-SIFAT OPERASI MATRIKS
 A+B = B+A
(hukum komutatif penjumlahan)
 A + ( B+C) = (A + B ) + C
(hukum asosiatif Penjumlahan
 A (B.C) = (A.B) .C
(hukum asosiatif perkalian)
 A (B+C) = A.B + A.C
 (B+C).A = B.A+ C.A
(hukum distributif)

13. Tranpose Matriks
Jika Matriks A berdimensi m x n
Maka Tranpose A ( A T ) berdimensi n x m
Baris menjadi kolom dan kolom menjadi baris
Sifat – Sifat
Transpos
[(AT)T] = A
(A +B) T = AT +BT
(A –B)T = AT - BT
(kA)T = k. AT ( k adalah konstanta)
(A.B)T = BT .AT

14. Contoh











4
4
4
4
2
6
7
5
2
A
Jika T
A
tentukan
Maka











4
4
7
4
2
5
4
6
2
T
A

15. TRACE SUATU MATRIKS BUJUR SANGKAR
 Jika A adalah matriks bujur sangkar, maka trace A
dinyatakan dengan tr(A) didefinisikan sebagai jumlah
anggota-anggota pada diagonal utama A.
 Trace A tidak terdefenisi jika A bukan matriks bujur
sangkar











4
4
4
4
2
6
7
5
2
A
Jika )
(A
tr
tentukan
Maka
8
4
2
2
)
( 



A
tr

16. SELESAI
(^_^)
LANJUT TUGAS YAA!! ^^

17. TUGAS
Tulis Jawaban di kertas Double Folio
.
7
4
5
1
3
2










A
Diketahui













3
1
2
3
0
2
/
1
B
!
B
A
dan
B
A
Tentukan 

D
C
dan
D
C
Tentukan 2
2 









3
0
0
2
D
1.
2.
.
4
1
3
2








C
Diketahui

18. 

















12
9
11
8
10
7
6
5
4
3
2
1
B
A
Jika
3.
4.
a. Tentukan A.B dan B.A
b. Tentukan A T dan B T
c. Tentukan (A T .B T) dan (B.A)T
)
( A
tr
tentukan
Maka

















0
1
2
4
3
7
2
1
4
8
5
3
0
7
2
1
A
Jika

19. 5. Jika A matriks berukuran (2x3), B berukuran (2x4), C berukuran
(3x3) dan D (3 x2). Tentukanlah bentuk atau ukuran matriks dari
hasil operasi A x C x Dx B !
6. Tentukan nilai x, y, z dan u dari persamaan matriks























2
2
3
4
2
1
3
z
u
z
y
x
u
z
y
x