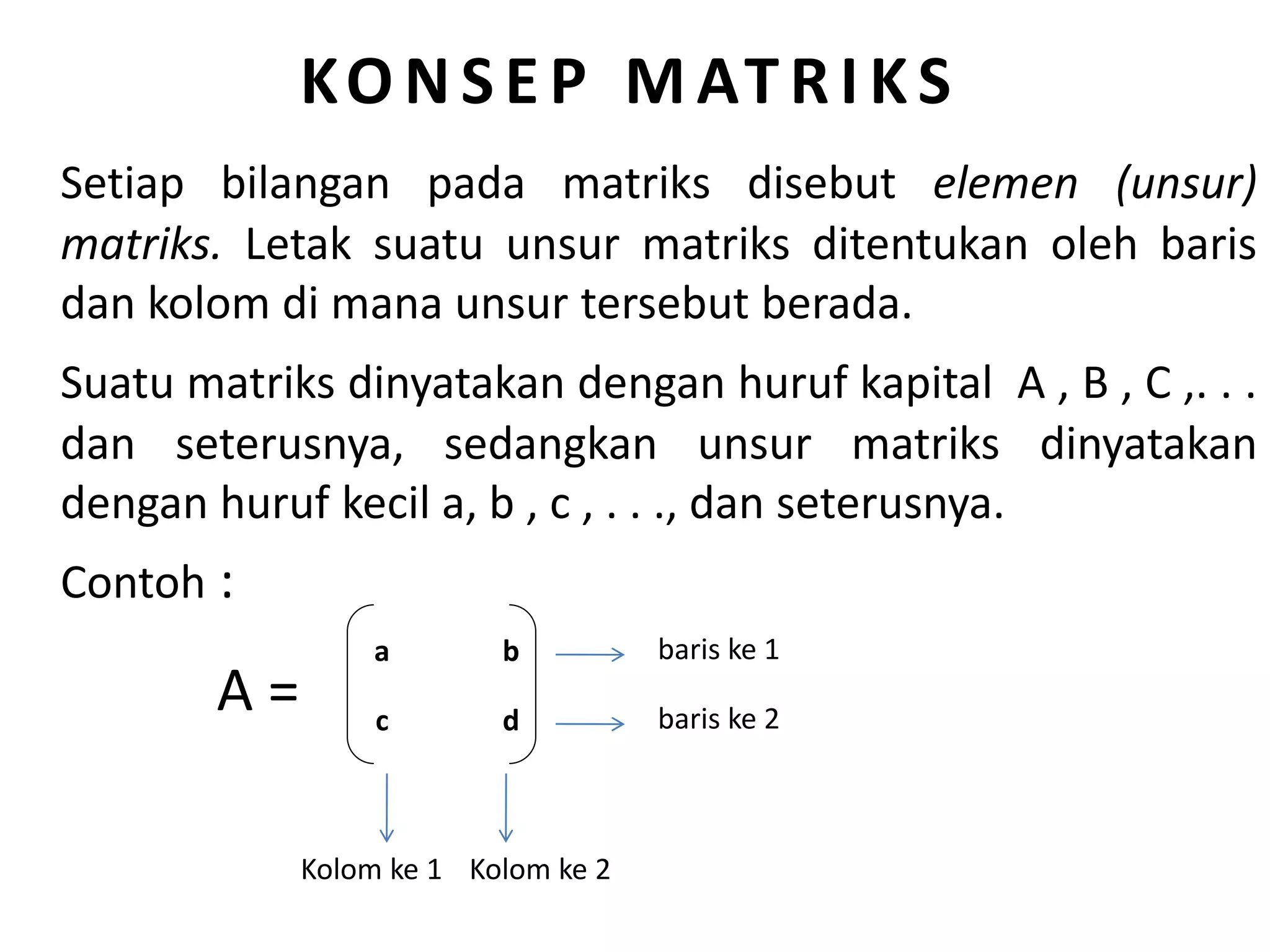
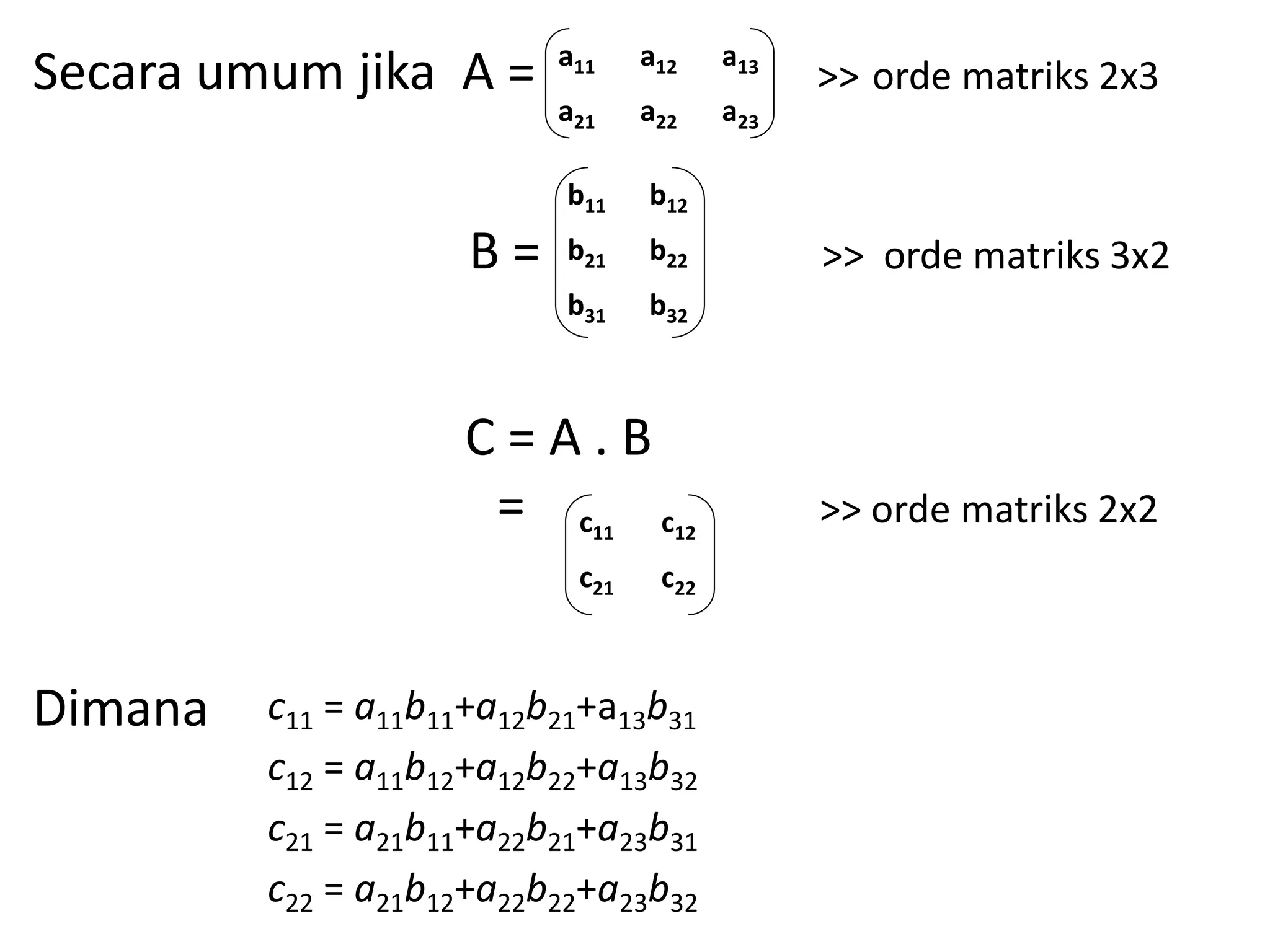
Dokumen ini menjelaskan konsep matriks, termasuk definisi, notasi, dan berbagai jenisnya, seperti matriks persegi, kolom, dan baris. Selain itu, dijelaskan cara operasi dasar seperti penjumlahan, pengurangan, dan perkalian matriks, serta sifat-sifatnya. Terdapat juga pembahasan tentang determinan matriks dan metode untuk menghitungnya, termasuk metode Sarrus dan ekspansi kofaktor.

1. M AT R I KS
Matriks adalah set bilangan real atau bilangan
kompleks (elemen-elemen) yang disusun dalam
Baris dan Kolom sehingga membentuk jajaran
persegi panjang (rectangular array)
Matriks adalah suatu susunan angka atau
bilangan, variabel, atau parameter yang
berbentuk empat persegi dan biasanya ditutup
dengan tanda kurung.

2. KONSEP MATRIKS
Setiap bilangan pada matriks disebut elemen (unsur)
matriks. Letak suatu unsur matriks ditentukan oleh baris
dan kolom di mana unsur tersebut berada.
Suatu matriks dinyatakan dengan huruf kapital A , B , C ,. . .
dan seterusnya, sedangkan unsur matriks dinyatakan
dengan huruf kecil a, b , c , . . ., dan seterusnya.
Contoh :
a b
c d
Kolom ke 1 Kolom ke 2
baris ke 1
baris ke 2
A =

3. Matriks A mempunyai dua baris dan dua kolom. Oleh
karena itu kita katakan bahwa matriks A berorde 2 X 2
ditulis A2X2 atau (a22).
“Orde suatu matriks ditentukan oleh banyaknya baris dan
banyaknya kolom dalam matriks tersebut.”
a b
c d
Kolom ke 1 Kolom ke 2
baris ke 1
baris ke 2
A =

4. 


















0
9
6
7
8
1
2
3
2
4
6
5
A Orde 4 x 3











0
2
3
1
4
6
A Orde 3 x 2









6
5
4
3
2
1
A Orde 2 x 3

5. Notasi Matriks















44
43
42
41
34
33
32
31
24
23
22
21
14
13
12
11
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
A
a23 menandakan
elemen dalam baris
kedua kolom ketiga






















1
7
9
2
5
6
7
4
3
8
4
2
3
1
5
6
A

6. KESAMAAN MATRIKS
Matriks A dan matriks B dikatakan berorde sama atau berukuran
sama jika banyaknya baris dan banyaknya kolom pada matriks A
sama dengan banyaknya baris dan banyaknya kolom pada
matriks B.
Contoh :
Matriks A berorde sama dengan matriks B, yaitu 2 x 3
Definisi:
Dua buah matriks A dan B dikatakan sama (ditulis A = B), jika :
a. Matriks A dan B mempunyai orde sama.
b. Unsur-unsur yang seletak pada matriks A dan matriks B sama.
a b c
d e f
A =
a b c
d e f
B =
dan

7. PENJUMLAHAN DAN
PENGURANGAN 2 MATRIKS
Dua matriks dapat dijumlahkan atau dikurangkan jika
ordenya sama.
Misal orde matriks A = 2 x 3 dan orde matriks B = 2 x 3,
maka keduanya dapat dijumlahkan atau dikurangkan.

8. CONTOH
Jika A = , dan B =
Maka A + B = =
A - B = =
3 2 1
5 4 6
7 5 -3
-2 1 0
3+7 2+5 1+(-3)
5+(-2) 4+1 6+0
10 7 -2
3 5 6
3-7 2-5 1-(-3)
5-(-2) 4-1 6-0
-4 -3 4
7 3 6

9. BEBERAPA SIFAT YANG
BERLAKU PADA PENJUMLAHAN
/PENGURANGA N MATRIKS
1) A + B = B + A ( Sifat Komutatif)
2) (A + B) + C = A + ( B + C) (Sifat Asosiatif)
3) A + 0 = 0 + A = A (Sifat Identitas tambah)
4) A – B = - (B – A) (Sifat Komutatif)
5) A – B = - B + A ( Sifat Komutatif)

10. PERKALIAN BILANGAN REAL
DENGAN MATRIKS
Jika k adalah suatu bilangan Real (skalar) dan Matriks
A = (aij), maka Matriks kA = (kaij) adalah suatu matriks
yang di peroleh dengan mengalikan semua elemen
matriks A dengan k.
Jadi, jika A = , maka : kA =
Contoh : Misal A = ,
maka 3A = 3 = =
7 5 -3
-2 1 0
a11 a12
a21 a22
ka11 ka12
ka21 ka22
7 5 -3
-2 1 0
3.7 3.5 3.(-3)
3.(-2) 3.1 3.0
21 15 -9
-6 3 0

11. SIFAT-SIFAT PERKALIAN MATRIKS
DENGAN BILANGAN REAL
Jika a dan b bilangan real, maka :
• ( a + b )A = aA + bA
• a ( A + B ) = aA + aB
• a( bA ) = (ab)A

12. PERKALIAN MATRIKS DENGAN
MATRIKS (PERKALIAN 2 MATRIKS)
Matriks A yang berorde mxp dengan suatu matriks B
yang berorde pxn adalah matriks C yang berorde mxn.
A mxp.Bpxn = C mxn
Dalam perkalian matriks ini yang perlu
diperhatikan adalah : Dua buah matrik dapat
dikalikan apabila Jumlah kolom pada matriks A
(pertama) harus sama dengan banyaknya baris pada
matriks B (kedua). Jika hal ini tidak dipenuhi, maka
hasil kali matriks tidak didefinisikan.

13. 










0
2
3
1
4
6
C










3
0
5
1
1
2
D














2
3
1
5
2
4
0
1
3
E









4
2
1
3
F
 
1
2
3 

A











5
1
2
B
orde 1 x 3
orde 3 x 1
orde 3 x 2 orde 2 x 3
orde 3 x 3 orde 2 x 2

14. 


























2
3
1
5
2
4
0
1
3
2
3
1
5
2
4
0
1
3
2
x
E

















11
1
7
0
15
9
5
1
5

15. Secara umum jika A = >> orde matriks 2x3
B = >> orde matriks 3x2
C = A . B
= >> orde matriks 2x2
Dimana
a11 a12 a13
a21 a22 a23
b11 b12
b21 b22
b31 b32
c11 c12
c21 c22
c11 = a11b11+a12b21+a13b31
c12 = a11b12+a12b22+a13b32
c21 = a21b11+a22b21+a23b31
c22 = a21b12+a22b22+a23b32

16. Macam - macam MATRIKS
dan Matriks Khusus
Matriks Kolom adalah matriks yang terdiri dari
satu kolom
Contoh : A =
4
5
-1

17. MATRIKS BARIS
Matriks Baris adalah matriks yang terdiri dari
satu baris.
Contoh : A = ( 4 3 2 4 )

18. MATRIKS PERSEGI ATAU
MATRIKS BUJUR SANGKAR
Matriks Persegi atau matriks Bujur Sangkar
adalah matriks yang mempunyai jumlah baris
= jumlah kolom
Contoh :
Contoh : A = ,
4 5 -1
5 2 4
3 2 1
jumlah baris = jumlah kolom

19. MATRIKS NOL
Matriks Nol adalah Suatu matriks yang setiap
unsurnya 0 berordo m x n ,ditulis dengan
huruf O
Contoh : O3X3 =
0 0 0
0 0 0
0 0 0

20. MATRIKS SEGI TIGA
Matriks Segi Tiga adalah suatu matriks bujur
sangkar yang unsur-unsur dibawah atau diatas
diagonal utama semuanya 0 (nol).
Contoh : C = , D =
2 0 0 0
3 7 0 0
-9 0 8 0
4 1 -3 5
8 2 1 -3
0 6 5 4
0 0 3 7
0 0 0 9

21. MATRIKS DIAGONAL
Matriks Diagonal adalah suatu matriks bujur
sangkar yang semua unsurnya , kecuali unsur-
unsur pada diagonal utama adalah nol.
Contoh : E =
5 0 0 0
0 7 0 0
0 0 -2 0
0 0 0 8

22. MATRIKS SKALAR
Matriks Skalar adalah matriks diagonal yang
unsur-unsur pada diagonal utama semuanya
sama.
Contoh : F =
7 0 0 0
0 7 0 0
0 0 7 0
0 0 0 7

23. MATRIKS IDENTITAS ATAU
MATRIKS SATUAN
Matriks Identitas atau Matriks Satuan adalah
matriks diagonal yang unsur-unsur pada
diagonal utama semuanya 1 (satu) ditulis
dengan huruf I.
Contoh : I = , I =
I3 adalah matriks identitas ordo 3 dan I4 adalah matriks identitas ordo 4
1 0 0
0 1 0
0 0 1
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

24. MATRIKS SIMETRIS
Matriks Simetri adalah suatu matriks bujur
sangkar yang unsur pada baris ke-i kolom ke-j
sama dengan unsur pada baris ke-j kolom ke-i
sehingga aij = aji.
Contoh : G =
Unsur pada baris ke-2 kolom ke-4 adalah 9 dan unsur pada
baris ke-4 kolom ke-2 juga
1 3 2 5
3 4 6 9
2 6 7 8
5 9 8 2

25. MATRIKS MENDATAR
Matriks Mendatar adalah matriks yang
banyaknya baris kurang dari banyaknya kolom.
Contoh : H2X3 =
3 2 1
4 5 1

26. MATRIKS TEGAK
Matriks Tegak adalah suatu matriks yang
banyaknya baris lebih dari banyaknya kolom.
Contoh : K3x2 =
1 -8
4 1
9 1

27. MATRIKS TRANSPOS ( notasi AT )
Transpos A adalah matriks baru dimana elemen kolom
pertama = elemen baris pertama matriks A, elemen kolom
kedua = elemen baris kedua matriks A, elemen kolom ketiga
= elemen baris ketiga matriks A. Atau jika suatu matriks saling
dipertukarkan
Misal Matriks A =
Maka Transpos A adalah AT =
Jadi jika ordo matriks A = 3x4 maka ordo matriks transpos adalah 4x3
1 -2 5 8
9 1 4 2
0 3 -2 -3
1 9 0
-2 1 3
5 4 -2
8 2 -3

28. SIFAT-SIFAT MATRIKS TRANSPOS
1) ( A + B )T = AT + BT
2) ( AT )T = A
3) ( AB )T = BT AT

29. OPERASI MATRIKS

30. DETERMINAN MATRIKS
Determinan matriks 𝐴 di definisikan sebagai selisih
antara perkalian elemen - elemen pada diagonal
utama dengan perkalian elemen - elemen pada
diagonal sekunder. Determinan dari matriks
dinotasikan dengan det 𝐴 atau |𝐴|. Nilai dari
determinan suatu matriks berupa bilangan real.

31. DETERMINAN MATRIKS ORDO 2x2
Jika Matriks A = maka det (A) = |A| = | |= ad – bc
Contoh :
P = maka,
det (P) = |P| = | | = (2.3) – (1.(-6)) = 6+6 = 12
a b
c d
a b
c d
2 1
-6 3
2 1
-6 3

32. DETERMINAN MATRIKS ORDO 3x3
Untuk mencari determinanmatriks berordod
apatdigunakan dua metode, sebagaiberikut:
• MetodeSarrus
• MetodeEkspansiKofaktor

33. METODE SARRUS
Cara ini paling tepat digunakan untuk menentukan
determinan matriks ordo 3×3.
Cara sarrus :
i. Tuliskan kolom pertama dan kedua dari determinan
awal di sebelah kanan setelah kolom ketiga.
ii. Kalikan unsur – unsur pada keenam diagonal, yaitu
tiga kolom diagonal utama (dari kiri ke kanan) dan
tiga kolom diagonal pendamping (dari kanan ke kiri).
Hasil kali diagonal utama dijumlahkan dan hasil kali
pada diagonal pendamping dikurangkan.

34. Jika Matriks B =
maka det (B) = |B| =
= ptx + quv + rsw – vtr –wup – xsq
Perlu diperhatikan bahwa Metode Sarrus tidak berlaku
bila matriks berordo 4x4 dan yang lebih tinggi lagi.
p q r
s t u
v w x
p q r
s t u
v w x
p q
s t
v w

35. METODE EKSPANSI KOFAKTOR
a. Pengertian Minor . Minor suatu matriks 𝐴 dilambangkan
dengan 𝑀𝑖j adalah matriks bagian dari 𝐴 yang diperoleh
dengan cara menghilangkan elemen - elemennya pada
baris ke-𝑖 dan elemen elemen pada kolom ke-𝑗.
Contoh : A = maka,
A11 = , A12 = , A13 =
A11, A12 , A13 merupakan sub matriks hasil ekspansi baris
ke-1 dari matriks A
3 2 4
1 -7 5
7 -2 -3
-7 5
-2 -3
1 5
7 -3
1 -7
7 -2

36. b. Pengertian Kofaktor suatu elemen baris ke-𝑖 dan
kolom ke-𝑗dari matriks A dilambangkan dengan
𝐾𝑖j =(−1)𝑖+𝑗. |𝑀𝑖j| = (−1)𝑖+𝑗.det (𝑀𝑖.j)
Penentuan tanda dr determinan matriks persegi berodo 3x3 :
Untuk mencari det (A) dg metode ekspansi kofaktor cukup mengambil satu
ekspansi saja misal ekspansi bari ke -1
+ - +
- + -
+ - +

37. CONTOH
𝑄 =
Untuk mendapatkan det(𝑄) dengan metode kofaktor
adalah mencari terlebih dahulu determinan – determinan
minornya yang diperoleh dari ekspansi baris ke-1 diatas,
yaitu :
M11= , det(𝑀11) = 11 ; M12= , det(𝑀12) = -32 ;
M13= , det(𝑀13)=− 47
det(𝑄)= 𝑘11.𝑞11+𝑘12.𝑞12+𝑘13.𝑞13
= (−1)1+1.|𝑀11|.𝑞11+ (−1)1+2.|𝑀12|.𝑞12 + (−1)1+3.|𝑀13|.𝑞13
=11.3 − (−32).2 + (−47).4 =33+64−188 = −91
3 2 4
1 -7 5
7 -2 -3
-7 5
2 3
1 5
7 3
1 7
7 2

38. ADJOIN MATRIKS
Adjoin matriks A adalah transpose dari kofaktor-kofaktor matriks
tersebut, dilambangkan dengan adj A = CT
CONTOH :
k11= (-1)1+1 | =11 ; k12= (-1)1+2 =32 ;
k13= (-1)1+3 =−47 ; k21= (-1)2+1 =2 ;
k22= (-1)2+2 | |=−19 ; k23 = (-1)2+3 =8 ;
k31= (-1)3+1 =−18 ; k32= (-1)3+2 =−11
k33= (-1)3+3 =18
3 2 4
1 7 5
7 2 3
3 2
1 7
1 5
7 3
1 7
7 2
2 4
2 3
3 4
7 3
3 2
7 2
2 4
7 5
3 4
1 5
3 2
1 7

39. • Adj A = =
• Jika A= maka kofaktor-kofaktornya adalah
k11= d, k12 = − c, k 21= − b dan k 22 = a.
Kemudian Adj A = =
Hal ini sama artinya dengan menukarkan elemen-
elemen pada diagonal utamanya dan mengubah
tanda pada elemen-elemen pada diagonal lainnya.
k11 k12 k13
k21 k22 k23
k31 k32 k33
11 2 -18
32 -19 -11
-47 8 18
a b
c d
k11 k12
k21 k22
d -b
-c a

40. INVERS MATRIKS
Invers matriks adalah lawan atau kebalikan suatu matriks
dalam perkalian yang dilambangkan dengan A-1.
Definisi:
Jika matriks A dan B sedemikian sehingga A x B = B x A = I,
dimana I matriks identitas maka B disebut invers dari A
dan A invers dari B.
Karena invers matriks A dilambangkan dengan A-1 maka
berlaku: A x A-1 = A-1 x A = I
Dimana I adalah matrik identitas.

41. Matriks
determinan
Minor
Tanda Tempat
Kofaktor = C
Adjoin A = CT
Matriks Invers
A-1
=
1
Adj A
det A

42. Penyelesaian Set Persamaan Linier
Bentuk Matriksnya
n
n
nn
n
n
n
n
n
n
n
n
n
b
x
a
x
a
x
a
x
a
b
x
a
x
a
x
a
x
a
b
x
a
x
a
x
a
x
a
b
x
a
x
a
x
a
x
a




















......
.
.
......
......
......
3
3
2
2
1
1
3
3
3
33
2
32
1
31
2
2
3
23
2
22
1
21
1
1
3
13
2
12
1
11































3
2
1
3
2
1
33
32
31
23
22
21
13
12
11
.
b
b
b
x
x
x
a
a
a
a
a
a
a
a
a

43. 






























3
2
1
3
2
1
33
32
31
23
22
21
13
12
11
.
b
b
b
x
x
x
a
a
a
a
a
a
a
a
a
A . x = b
b
A
x
b
A
x
I
b
A
x
A
A
b
x
A dikaliA
.
.
.
.
.
.
.
1
1
1
1
1









 




44. Matriks x = A-1 b
determinan
Minor
Tanda Tempat
Kofaktor = C
Adjoin A = CT
Matriks Invers
A-1
=
1
Adj A
det A

45. INVERS MATRIKS ORDO 2×2
Rumus Invers Matriks Berordo 2 × 2
Misalkan A = invers dari A adalah A-1,
yaitu
• A -1 = , dengan det A ≠ 0
2 1
-3 -2








a
c
b
d
A
det
1

46. Contoh :
Tentukan invers dari matriks D =
Jawab :
det D = = 3(11) – (–7)(–6) = 33 – 42 = –9
D -1=
=
=
=








11
7
6
3








11
7
6
3






3
7
6
11
det
1
A






 3
7
6
11
9
1














9
3
9
7
9
6
9
11














3
1
9
7
3
2
9
11

47. INVERS MATRIKS ORDO 3×3
Contoh: B = , tentukan B-1!
Untuk mencari determinan matriks B, cara paling praktis
adalah dengan metode kofaktor dengan mengekspansi baris
yang memuat nol terbanyak yaitu baris ke-3, maka :
Det(B) = |B| = k31 . b31 + k32 . b32 + k33 . B33
= (-1)3+1 .0+(-1)3+2 .0+(-1)3+3 .6
= 0 + 0 + 24 = 24
1 2 3
0 4 5
0 0 6






5
4
3
2






5
0
3
1






4
0
2
1

50. MENYELESAIKAN
SISTEM PERSAMAAN LINEAR
Penyelesaian Sistem Persamaan Linear Dua Variabel
=
x
y
1
ad - bc
d -b
-c -a
p
q

51. CONTOH
TENTUKAN HIMPUNAN PENYELESAIANSISTEM PERSAMAAN
LINIER BERIKUT
2x + y = 4
3x + 2y = 9
=
2 1
-3 -2
x
y
4
9

52. Persamaan Matriks diatas dapat ditulis menjadi
AX =B, A = , X = , B =
det A = | | = 1 dan A-1 = 1/1 =
Oleh karena itu, X =A-1B  = =
Jadi, HP adalah {(-1, 6)}
2 1
-3 -2
x
y
4
9
2 1
-3 -2
2 1
-3 -2
2 1
-3 -2
x
y
2 1
-3 -2
4
9
-1
6

53. METODE CRAMER
• metode cramer didasarkan atas perhitungan
determinan matriks. Suatu sistem persamaan
linier Ax = b dengan A adalah matriks bujur
sangkar dapat di kerjakan dengan metode
cramer, jika hasil perhitungan menunjukkan
bahwa det(A)≠0.

58. Metode Eliminasi Gauss
n
n
nn
n
n
n
n
n
n
n
n
n
b
x
a
x
a
x
a
x
a
b
x
a
x
a
x
a
x
a
b
x
a
x
a
x
a
x
a
b
x
a
x
a
x
a
x
a




















......
.
.
......
......
......
3
3
2
2
1
1
3
3
3
33
2
32
1
31
2
2
3
23
2
22
1
21
1
1
3
13
2
12
1
11































3
2
1
3
2
1
33
32
31
23
22
21
13
12
11
.
b
b
b
x
x
x
a
a
a
a
a
a
a
a
a
A.x = b

59. Matriks diperbesar (Augmented Matrix)
11 12 1 1
21 22 2 2
1 2
n
n
m m mn m
a a a b
a a a b
a a a b
 
 
 
 
 
 
Operasi Baris Elementer:
• Faktor pengali a21/a11 dan a31/a11
• Baris pertama tetap
• Kurangkan baris kedua dengan mengalikan baris pertama
dengan a21/a11 atau = B2 - (a21/a11) B1
• Kurangkan baris ketiga dengan mengalikan baris
pertama dengan a31/a11 atau = B3 - (a31/a11) B1
• Baris pertama, baris kedua dan kolom pertama tetap
• Dst

60. Contoh:
Selesaikan SPL dengan MEG
Jawab:
Matriks yang diperbesar
1 2 3
1 2 3
1 2 3
2 8
2 3 1
3 7 4 10
x x x
x x x
x x x
  
   
  
1 1 2 8
1 2 3 1
3 7 4 10
 
 
 
 
 

 

61. 1 1 2 8
1 2 3 1
3 7 4 10
 
 
 
 
 

 
1 1 2 8
0 1 5 9
3 7 4 10
 
 

 
 

 
1 1 2 8
0 1 5 9
0 10 2 14
 
 

 
 
  
 
1 1 2 8
0 1 5 9
0 10 2 14
 
 
 
 
 
  
 
1 1 2 8
0 1 5 9
0 0 52 104
 
 
 
 
 
 
 
1
52

1 1 2 8
0 1 5 9
0 0 1 2
 
 
 
 
 
 
B2 + B1

B3 – 3B1

B2(–1 )

B3+10 B2

B3( )

Matriks yang terakhir bersesuaian dengan SPL
1 2 3
2 3
3
2 8
5 9
2
x x x
x x
x
  
  

Dengan melakukan substitusi balik akan
diperoleh
Sampai langkah ini, matriksnya kita sebut
matriks eselon baris (metode Eliminasi
Gauss).
1 2 3
3, 1, 2
x x x
  

62. Jika dilanjutkan…
1 1 2 8
0 1 5 9
0 0 1 2
 
 
 
 
 
 
1 0 7 17
0 1 5 9
0 0 1 2
 
 
 
 
 
 
1 0 0 3
0 1 5 9
0 0 1 2
 
 
 
 
 
 
1 0 0 3
0 1 0 1
0 0 1 2
 
 
 
 
 
B1 – B2 B1 – 7B3 B2+5B3
.
1 2 3
3, 1, 2
x x x
  
Diperoleh hasil yang sama,
Matriks tersebut dinamakan matriks eselon baris
tereduksi dan metodenya disebut eliminasi Gauss-
Jordan.

63. Determinan matriks 4 x 4

65. Nilai Determinan = A1 + A2 + A3