3. Pengertian Dasar Matriks
Matrik adalah susunan teratur bilangan-bilangan dalam baris
dan kolom yang membentuk suatu susunan persegi panjang
yang kita perlakukan sebagai suatu kesatuan.
Contoh:
123
421
302
baris
kolom
Nama matriks: huruf besar cetak tebal,
=
123
421
302
A
=
203
142
B
Contoh:
Notasi:
Bilangan ini bisa berupa
bilangan nyata atau kompleks.
Kita akan melihat matriks
berisi bilangan nyata.
4. Pengertian Dasar Matriks
Elemen Matriks
Isi suatu matriks disebut elemen matriks
Contoh:
=
203
142
B
2, 4, 1 dan 3, 0, 2 adalah elemen-emenen
matriks yang membentuk baris
2, 3 dan 4, 0, dan 1, 2 adalah elemen-elemen
matriks yang membentuk kolom
Ukuran Matriks
Secara umum suatu matrik terdiri dari b baris dan k kolom, sehingga
suatu matrik akan terdiri dari b×k elemen-elemen
Ukuran matriks dinyatakan sebagai b×k
Contoh:
=
203
142
B adalah matriks berukuran 2×3
5.
=
123
421
302
A
b = k = 3
matriks bujur
sangkar 3×3
Nama Khusus
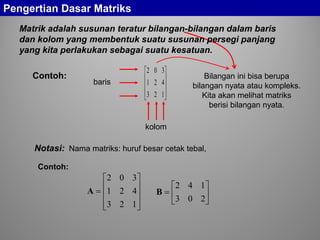
Pengertian Dasar Matriks
Matriks dengan b = k disebut matriks bujur sangkar.
Matriks dengan k = 1 disebut matriks kolom atau vektor kolom.
Matriks dengan b = 1 disebut matriks baris atau vektor baris.
Matriks dengan b ≠ k disebut matrik segi panjang
Contoh:
=
203
142
B
b = 2, k = 3
matriks segi
panjang 2×3
=
4
2
p k = 1
vektor kolom [ ]423=q b = 1
vektor baris
Notasi nama vektor: huruf kecil cetak tebal
6. Secara umum, matriks A dapat kita tuliskan sebagai
[ ]bk
mnmm
n
n
a
aaa
aaa
aaa
=
=
21
22221
11211
A
elemen-elemen a11 …amn disebut diagonal utama
Diagonal Utama
Pengertian Dasar Matriks
7. Matriks Segitiga
Contoh:
Pengertian Dasar Matriks
Matriks segitiga bawah :
−=
343
011
002
1T
Matriks segitiga atas :
−
=
300
310
122
2T
Ada dua macam matriks segitiga yaitu
matriks segitiga bawah dan matriks segitiga atas
Matriks segitiga bawah adalah matriks yang elemen-elemen di atas
diagonal utamanya bernilai nol.
Matriks segitiga atas adalah matriks yang elemen-elemen di bawah
diagonal utamanya bernilai nol.
8. Matriks Diagonal
Pengertian Dasar Matriks
Matriks diagonal adalah matriks yang elemen-elemen di atas maupun
di bawah diagonal utamanya bernilai nol.
Contoh:
=
000
010
002
D
9. Matriks Satuan
Pengertian Dasar Matriks
Jika semua elemen pada diagonal utama adalah 1, sedang elemen
yang lain adalah 0, matriks itu disebut matriks satuan.
Contoh:
IA =
=
100
010
001
Matriks Nol
Matriks nol, 0, yang berukuran m×n adalah matriks yang
berukuran m×n dengan semua elemennya bernilai nol.
10. Anak matriks atau sub-matriks
=
203
142
B
[ ]142 [ ]203- Dua anak matriks 1× 3 , yaitu:
3
2
0
4
2
1
- Tiga anak matriks 2× 1, yaitu:
- Enam anak matriks 1× 1 yaitu: [2] , [4] , [1] , [3] , [0] , [2];
- Enam anak matriks 1× 2 yaitu: [ ]42 [ ]12 [ ]14
[ ]03 [ ]23 [ ]20
03
42
23
12
20
14- Tiga anak matriks 2×2 yaitu:
Pengertian Dasar Matriks
Contoh:
Matriks B memiliki:
11. Matriks dapat dipandang sebagai tersusun dari anak-anak
matriks yang berupa vektor-vektor
=
123
421
302
A
=
3
2
1
a
a
a
Adapat kita pandang sebagai matriks
dengan anak-anak matriks berupa vektor baris
[ ]3021 =a [ ]4212 =a [ ]1233 =a
dapat kita pandang sebagai matriks [ ]321 aaaA =
=
3
1
2
1a
=
2
2
0
2a
=
1
4
3
3a
dengan anak-anak matriks yang berupa vektor kolom
Pengertian Dasar Matriks
Contoh:
Contoh yang lain:
=
123
421
302
A
12.
13. Kesamaan Matriks
Dua matriks A dan B dikatakan sama jika dan hanya jika berukuran
sama dan elemen-elemen pada posisi yang sama juga sama.
A = B
=
03
42
AJika
=
03
42
Bmaka haruslah .
Operasi Matriks, Kesamaan, Matriks Nol, Matriks negatif
Contoh:
14. Matriks Negatif
Negatif dari matriks berukuran m×n adalah matriks berukuran
m×n yang diperoleh dengan mengalikan seluruh elemennya
dengan faktor (−1). .
Operasi Matriks, Kesamaan, Matriks Nol, Matriks negatif
Contoh:
=
03
42
A
−
−−
=−
03
42
A
15. Penjumlahan
Penjumlahan dua matriks hanya didefinisikan
untuk matriks yang berukuran sama
Jumlah dari dua matriks A dan B yang masing-masing berukuran
m×n adalah sebuah matriks C berukuran m×n yang elemen-
elemennya merupakan jumlah dari elemen-elemen matriks A dan
B yang posisinya sama
ABBA +=+
( ) ( )CBACBA ++=++
=
03
42
A
=
22
31
B
Jika
=+
25
73
BAmaka
Sifat-sifat penjumlahan matriks:
Operasi Matriks, Penjumlahan dan Pengurangan
Contoh:
16. Pengurangan Matriks
Pengurangan matriks dapat dipandang sebagai
penjumlahan dengan matriks negatif
A0A =+
0AAAA =−+=− )(
=
03
42
A
=
22
31
B
−
=
−−
−−
+
=−
21
11
22
31
03
42
BA
Contoh:
Operasi Matriks, Penjumlahan dan Pengurangan
17. Perkalian Matriks
=
mnmm
n
n
aaa
aaa
aaa
21
22221
11211
A
=
pqmp
q
q
aaa
aaa
aaa
21
22221
11211
B
Jadi jika matriks A berukuran m×n dan B berukuran p×q
maka perkalian AB hanya dapat dilakukan jika n = p.
Operasi Matriks, Penjumlahan dan Pengurangan
BAAB ≠
Hasil kali matriks AB berupa matriks berukuran m×q dengan nilai elemen
pada baris ke b kolom ke k merupakan hasil kali internal (dot product) vektor
baris ke b dari matriks A dan vektor kolom ke k dari matriks B
Perkalian antara dua matriks A dan B yaitu C = AB hanya terdefinisikan jika
banyak kolom matriks A sama dengan banyak baris matriks B.
Dalam perkalian matriks, urutan hatus diperhatikan.
Perkalian matriks tidak komutatif.
18. Perkalian Matriks dengan Bilangan Skalar
Hasil kali suatu bilangan skalar a dengan matriks berukuran m×n
adalah matriks berukuran m×n yang seluruh elemennya bernilai a kali.
aA = Aa
=×
=
×
646
462
244
2
323
231
122
323
231
122
2
Perkalian matriks dengan bilangan skalar ini mempunyai sifat-sifat
sebagai berikut
( ) BABA aaa +=+
( ) AAA baba +=+
[ ] ( )AA abba =
Operasi Matriks, Perkalian Matriks
Contoh:
19. Perkalian Internal Vektor (dot product)
[ ]32=a
=
3
4
bvektor baris: vektor kolom:
.
Contoh:
2 kolom
2 baris
Perkalian internal antara dua vektor a dan b yaitu c = ab hanya
terdefinisikan jika banyak kolom vektor a sama dengan banyak baris
vektor b.
Dalam perkalian internal vektor, urutan perkalian harus diperhatikan.
[ ] [ ] [ ]173342
3
4
32 =×+×=
=•= bac
Jika urutan dibalik, b : 1 kolom, a : 1 baris, perkalian juga dapat dilakukan
tetapi memberikan hasil yang berbeda
[ ]
=
××
××
=
=•=
96
128
3323
3424
32
3
4
abd
perkalian internal dapat dilakukan
Perkalian matriks tidak komutatif.
Operasi Matriks, Perkalian Matriks
20. Perkalian Matriks Dengan Vektor
=
43
12
A
=
3
2
bMisalkan dan
dapat dikalikan2 kolom
2 baris
=
×+×
×+×
=
•
•
=
==
18
7
3423
3122
2
1
2
1
ba
ba
b
a
a
AbC
Jika urutan perkalian dibalik, perkalian tidak dapat dilakukan
karena b terdiri dari satu kolom sedangkan A terdiri dari dua baris.
Contoh:
Operasi Matriks, Perkalian Matriks
21. Perkalian Dua Matriks Bujur Sangkar
Operasi Matriks, Perkalian Matriks
=
43
12
A
=
35
24
Bdan
Contoh:
dapat dikalikan
kolom = 2
baris = 2
Matriks A kita pandang sebagai
=
2
1
a
a
A
Matriks B kita pandang sebagai [ ]21 bbB =
[ ]
=
×+××+×
×+××+×
=
••
••
=
==
1832
713
34235443
31225142
2212
2111
21
2
1
baba
baba
bb
a
a
ABC
23.
=
2
1
a
a
A [ ]21 bbB =
[ ]
••
••
=
==
2212
2111
21
2
1
baba
baba
bb
a
a
ABC
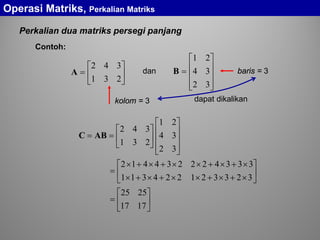
Pernyataan matriks dengan anak matriks pada contoh di atas adalah
,
sehingga
.
Operasi Matriks, Perkalian Matriks
Dalam operasi perkalian matriks:
matriks yang pertama kita susun dari anak matriks yang berupa
vektor baris
matriks yang kedua kita susun dari anak matriks yang berupa
vektor kolom
Jadi perkalian matriks adalah perkalian dari baris ke kolom
24. ( ) ( ) ( )BAABBA aaa ==
( ) ( )CABBCA =
( ) BCACCBA +=+
( ) CBCABAC +=+
Sifat-sifat perkalian matriks
b. Tidak komutatif. Jika perkalian AB maupun BA terdefinisikan,
maka pada umumnya AB ≠ BA
a. Asosiatif dan distributif terhadap penjumlahan
Jika AB = 0 tidak selalu berakibat A = 0 atau B = 0.
c. Hukum pembatalan tidak selalu berlaku.
Operasi Matriks, Perkalian Matriks
25.
26. Putaran Matriks
Putaran Matriks (Transposisi)
Putaran matriks atau transposisi dari matriks A berukuran m×n
adalah suatu matriks AT yang berukuran n×m dengan kolom-
kolom matriks A sebagai baris-barisnya yang berarti pula bahwa
baris-baris matriks A menjadi kolom-kolom matriks AT
[ ]bk
mnmm
n
n
a
aaa
aaa
aaa
=
=
21
22221
11211
A
[ ]pq
mnnn
m
m
a
aaa
aaa
aaa
=
=
21
22212
12111
T
A
Jika
maka
27. Putaran Vektor Baris Dan Vektor Kolom
Putaran Matriks
Putaran vektor baris akan menjadi vektor kolom.
Sebaliknya putaran vektor kolom akan menjadi vektor baris.
[ ]
=⇒=
3
4
2
342 T
aa
[ ]345
3
4
5
T
=⇒
= bb
Contoh:
28. Putaran Jumlah Dua Vektor Baris
Putaran Matriks
Putaran jumlah dua vektor baris sama dengan
jumlah putaran masing-masing vektor
[ ] [ ]231dan342 == ba
[ ]573=+ ba
( ) TTT
2
3
1
3
4
2
5
7
3
baba +=
+
=
=+
( ) TTT
baba +=+
Jika
maka
Secara umum :
Contoh:
29. Putaran Hasil Kali Vektor Baris Dan Vektor Kolom
Putaran Matriks
Putaran hasil kali vektor baris dengan vektor kolom atau vektor
kolom dengan vektor baris, sama dengan hasil kali putaran
masing-masing dengan urutan dibalik
[ ]
==
2
3
1
dan342 ba
[ ]233412 ×+×+×=ab
Jika
maka
Contoh:
[ ] [ ] TTT
3
4
2
231233412 abab =
=×+×+×=
31. Putaran Matriks
Contoh:
Putaran Matriks Persegi Panjang
=
231
342
A
=
23
34
12
T
AJika maka
=
ma
a
A
1
[ ]TT
1
T
maaA =
Jika matriks A dinyatakan
sebagai susunan dari
vektor baris
maka
[ ]maaaA 21=
Jika matriks A
dinyatakan dengan
vektor kolom
=
ma
a
A
1
T
maka
32. Putaran Matriks
Putaran Jumlah Matriks
Putaran jumlah dua matriks sama dengan jumlah putaran masing-
masing matriks.
Hal ini telah kita lihat pada putaran jumlah vektor baris.
( ) TTT
BABA +=+
[ ]maaA 1= [ ]mbbB 1=
[ ]mm babaBA ++=+ 11
Jika
Dengan demikian
dan
maka
( )
( )
( )
TT
T
T
1
T
T
1
TT
T
1
T
1
T
T
11
T
BA
b
b
a
a
ba
ba
ba
ba
BA +=
+
=
+
+
=
+
+
=+
mmmmmm
33. Putaran Hasil Kali Matriks
Putaran hasilkali dua matriks sama dengan hasil kali putaran
masing-masing dengan urutan yang dibalik. Hal ini telah kita lihat
pada putaran hasil kali vektor baris dan vektor kolom.
( ) TTT
ABAB =
=
ma
a
A
1
[ ]nbbB 1=
••
••
=
nmnm
n
baba
baba
AB
111
Jika dan
maka
[ ] TT
1
1111
T
ABaa
b
b
baba
baba
AB =
=
••
••
= m
nnmnm
n
Dengan demikian maka
Putaran Matriks
34. Putaran Matriks
Matriks Simetris
Jika
dikatakan bahwa matriks B adalah simetris miring.
BB −=T
Matriks simetris adalah matriks yang putarannya sama dengan
matriksnya sendiri. Jadi matriks A dikatakan simetris apabila
AA =T
Karena dalam setiap putaran matriks nilai
elemen-elemen diagonal utama tidak berubah,
maka matriks simetris miring dapat terjadi jika
elemen diagonal utamanya bernilai nol.
Berkaitan dengan putaran matriks, kita mengenal kesimetrisan pada
matriks nyata.
35.
36. Determinan Matriks
Determinan Matriks
Jika A adalah suatu matriks bujur sangkar, maka kita mengaitkan A
dengan suatu bilangan yang dinyatakan oleh
△=
𝑎11 𝑎12 𝑎13 ⋯ 𝑎1𝑛
𝑎21
⋮
𝑎22
⋮
𝑎23
⋮
⋯
𝑎2𝑛
⋮
𝑎 𝑛𝑛 𝑎 𝑛𝑛 𝑎 𝑛𝑛 ⋯ 𝑎 𝑛𝑛
Yang dinamakan determinan dari A dengan ukuran n, ditulis det(A).
Untuk mendefinisikan nilai suatu determinan, kita harus mengenal
beberapa konsep berikut:
1. Minor. Diberikan suatu unsur 𝑎𝑗𝑗 dari △. Suatu determinan
berukuran (𝑛 − 1) yang diperoleh dengan menghilangkan semua
unsure di baris ke j dan kolom ke k dinamakan minor dari 𝑎𝑗𝑗 .
37. Determinan Matriks
Contoh:
Minor yang bersesuaian dengan unsur 5 dalam baris ke-2 kolom
ke-3 dari determinan berukuran 4.
2 −1 𝟏 3
−𝟑 𝟐 𝟓 𝟎
1
4
0
−2
−𝟐
𝟑
2
1
adalah
2 −1 3
1 0 2
4 −2 1
Yang diperoleh dengan menghilangkan unsur-unsur yang
berwarna gelap.
38. Determinan Matriks
2. Kofaktor. Jika minor dari 𝑎𝑗𝑗 dikalikan dengan (−1) 𝑗+𝑘
, maka
hasilnya dinamakan kofaktor dari 𝑎𝑗𝑗 dan dinyatakan dengan
𝐴𝑗𝑗 .
Contoh:
Kofaktor yang bersesuaian dengan unsure 5 dalam
determinan pada contoh di atas adalah (−1)2+3 dikalikan
minornya, atau
−1
2 −1 3
1 0 2
4 −2 1
Nilai determinan didefinisikan sebagai jumlah dari hasil kali unsur-
unsur pada suatu baris atau kolom dengan kofaktor-kofaktor yang
bersesuaian, dan ini dinamakan uraian Laplace. Dalam lambang
ditulis:
det 𝐴 = � 𝑎𝑗𝑗 𝐴𝑗𝑗
𝑛
𝑘=1
39. Determinan Matriks
Menghitung determinan berukuran 2 menggunakan uraian Laplace:
𝑎11 𝑎12
𝑎21 𝑎22
menggunakan unsur di baris pertama. Kofaktor yang
berkaitan adalah
𝐴11 = (−1)1+1
𝑎22 = 𝑎22, 𝐴12 = (−1)1+2
𝑎21 = −𝑎21
Menurut uraian Laplace, determinannya bernilai
𝑎11 𝐴11 + 𝑎12 𝐴12 = 𝑎11 𝑎22 − 𝑎12 𝑎21
40. Determinan Matriks
Contoh:
Hitunglah uraian Laplace dari determinan
3 −2 2
1 2 −3
4 1 2
dengan
menggunakan unsur baris pertama.
Dengan menggunakan unsur baris pertama, uraiannya adalah
3
2 −3
1 2
— 2
1 −3
4 2
+ 2
1 2
4 1
= 3 7 − −2 14 + 2 −7 = 35
Nilai determinan orde 3 juga dapat dihitung menggunakan cara di bawah
ini:
𝑎1 𝑏1 𝑐1
𝑎2 𝑏2 𝑐2
𝑎3 𝑏3 𝑐3
= 𝑎1 𝑏2 𝑐3 + 𝑏1 𝑐2 𝑎3 + 𝑐1 𝑎2 𝑏3 − 𝑏1 𝑎2 𝑐3 + 𝑎1 𝑐2 𝑏3 + 𝑐1 𝑏2 𝑎3
Kemudian dengan mengambil jumlah hasil kali suku-suku yang
ditunjukkan dengan anak panah bertanda + dan −.
41. Determinan Matriks : Teorema
TEOREMA-TEOREMA DETERMINAN
1. Nilai suatu determinan tetap sama jika baris dan kolomnya
ditukar. Dalam lambang det 𝐴 = det (𝐴 𝑇
) .
2. Jika A dan B dua matriks bujursangkar yang berukuran sama,
maka det 𝐴𝐴 = det 𝐴 det (𝐵).
3. Jumlah dari hasil kali unsur-unsur pada suatu baris atau kolom
dengan kofaktor-kofaktor dari baris atau kolom lainnya adalah
nol. Dalam lambang ditulis:
� 𝑎 𝑞𝑞 𝐴 𝑝𝑝 = 0 atau
𝑛
𝑘=1
� 𝑎 𝑘𝑘 𝐴 𝑘𝑘 = 0 jika 𝑝 ≠ 𝑞
𝑛
𝑘=1
Jika 𝑝 = 𝑞 , jumlahnya sama dengan
det 𝐴 = � 𝑎𝑗𝑗 𝐴𝑗𝑗
𝑛
𝑘=1
42. Determinan Matriks : Teorema
4. Misalkan 𝑣1, 𝑣2, … , 𝑣 𝑛 menyatakan vector baris atau vector
kolom dari suatu matriks bujursangkar A yang berukuran n. Maka
det (A) = 0 jika dan hanya jika ada konstanta (scalar) 𝜆1, 𝜆2, … , 𝜆 𝑛
yang tidak semua nol sehingga
𝜆1 𝑣1 + 𝜆2 𝑣2 + ⋯ + 𝜆 𝑛 𝑣 𝑛 = 𝑂
Di mana O adalah matriks baris nol. Jika syarat di atas dapat
dipenuhi maka kita menyatakan bahwa vektor-vektor 𝑣1, 𝑣2, … , 𝑣 𝑛
bergantungan linear. Jika tidak demikian kita menyatakannya
bebas linear. Suatu matriks A sehingga det (A) = 0 dinamakan
matriks singular. Jika det (A) ≠ 0, maka A dinamakan matriks tak-
singular.
43.
44. Invers Matriks
Jika untuk suatu matriks bujursangkar A terdapat suatu matrik B
sehingga AB = I, maka dinamakan invers dari A dan dinyatakan
dengan 𝐴−1
. Dasarnya adalah rumus berikut ini:
Jika A suatu matriks tak singular berukuran n (det (A) ≠ 0) maka
terdapat tepat satu invers 𝐴−1 sehingga 𝐴𝐴−1 = 𝐴−1 𝐴 = 𝐼 dan kita
dapat menyatakan 𝐴−1
dalam bentuk
𝐴−1 =
(𝐴𝑗𝑗) 𝑇
det 𝐴
Di mana (𝐴 𝑗𝑗) adalah matriks dari kofaktor 𝐴𝑗𝑗 dan (𝐴𝑗𝑗) 𝑇
= (𝐴 𝑘𝑘)
adalah transposenya.
Bentuk berikut ini menyatakan sifat invers matriks:
(𝐴𝐴)−1
= 𝐵−1
𝐴−1
, (𝐴−1
)−1
= 𝐴
Contoh:
Tentukanlah invers matriks 𝐴 =
3 −2 2
1 2 −3
4 1 2
45. Invers Matriks
MATRIKS TEGAK LURUS (ORTHOGONAL)
Suatu matriks riil A dinamakan suatu matriks tegak lurus
(orthogonal) jika trnsposenya sama dengan inversnya, yaitu
jika 𝐴 𝑇
= 𝐴−1
atau 𝐴 𝑇
𝐴 = 𝐼.
46.
47. Nilai Eigen dan Vektor Eigen
Misalkan 𝐴 = 𝑎𝑗𝑗 adalah suatu matirks 𝑛 × 𝑛 dan X suatu vektor
kolom. Persamaan
𝐴𝐴 = 𝜆𝜆
Di mana suatu bilangan dapat ditulis sebagai
𝑎11 𝑎12 𝑎13 ⋯ 𝑎1𝑛
𝑎21
⋮
𝑎22
⋮
𝑎23
⋮
⋯
𝑎2𝑛
⋮
𝑎 𝑛𝑛 𝑎 𝑛𝑛 𝑎 𝑛𝑛 ⋯ 𝑎 𝑛𝑛
𝑥1
𝑥2
⋮
𝑥 𝑛
= 𝜆
𝑥1
𝑥2
⋮
𝑥 𝑛
Atau
𝑎11 − 𝜆 𝑥1 + 𝑎12 𝑥2 + ⋯ + 𝑎1𝑛 𝑥 𝑛 = 0
𝑎21 𝑥1 + 𝑎22 − 𝜆 𝑥2 + ⋯ + 𝑎2𝑛 𝑥 𝑛 = 0
… … … … … … … … … … … … … … … … …
𝑎 𝑛𝑛 𝑥1 + 𝑎 𝑛𝑛 𝑥2 + ⋯ + 𝑎 𝑛𝑛 − 𝜆 𝑥 𝑛 = 0
48. Nilai Eigen dan Vektor Eigen
Akan memiliki penyelesaian tak-trivial jika dan hanya jika
𝑎11 − 𝜆 𝑎12 ⋯ 𝑎1𝑛
𝑎21 𝑎22 − 𝜆 ⋯ 𝑎2𝑛
⋮
𝑎 𝑛𝑛
⋮
𝑎 𝑛𝑛
⋯
⋮
𝑎 𝑛𝑛 − 𝜆
= 0
Yang merupakan suatu persamaan suku banyak berderajat n
dalam 𝜆. Akar dari persamaan suku banyak ini dinamakan nilai
eigen atau nilai karakteristik (nilai ciri) dari matriks A. Bersesuaian
dengan setiap nilai eigen aka nada penyelesaian 𝑋 ≠ 0 yang
merupakan suatu penyelesaian tak-trivial, yang dinamakan suatu
vektor eigen atau vektor karakteristik dari nilai eigennya.
Persamaan juga dapat ditulis
det 𝐴 − 𝜆𝜆 = 0
Dan persamaan dalam 𝜆 ini seringkali dinamakan persamaan
karakteristik.
49. Nilai Eigen dan Vektor Eigen
TEOREMA PADA NILAI EIGEN DAN VEKTOR EIGEN
Reduksi suatu matriks ke bentuk diagonal. Jika suatu matriks tak
singular A mempunyai nilai eigen yang berbeda-beda 𝜆1, 𝜆2, 𝜆3, … …
dengan vektor eigen yang berkaitan ditulis sebagai kolom dari matriks
𝐵 =
𝑏11 𝑏12 𝑏13 ⋯
𝑏21 𝑏22 𝑏23 ⋯
⋯ ⋯ ⋯ ⋯
Maka 𝐵−1
𝐴𝐴 =
𝜆1 0 0 ⋯
0 𝜆2 0 ⋯
0
⋯
0
⋯
𝜆3
⋯
⋯
⋯
Yaitu 𝐵−1
𝐴𝐴 dinamakan transformasi dari A oleh B, yang merupakan
matriks diagonal yang memuat nilai eigen dari A dalam diagonal
utamanya dan unsur lainnya nol. Kita mengatakan bahwa A telah
ditransformasikan atau di direksikan ke bentuk diagonal.
50. Nilai Eigen dan Vektor Eigen
TEOREMA PADA NILAI EIGEN DAN VEKTOR EIGEN
Contoh:
Transformasikan matriks ke dalam bentuk diagonal 𝐵 =
2 1 −1
1 1 1
3 2 1
51. Nilai Eigen dan Vektor Eigen
TEOREMA PADA NILAI EIGEN DAN VEKTOR EIGEN
Reduksi bentuk kuadrat ke bentuk kanonik. Misalkan A suatu matriks
riil setangkup, sebagai contoh
𝐴 =
𝑎11 𝑎12 𝑎13
𝑎21 𝑎22 𝑎23
𝑎31 𝑎32 𝑎33
𝑎12 = 𝑎21, 𝑎13 = 𝑎31, 𝑎23 = 𝑎32
Jika 𝑋 =
𝑥1
𝑥2
𝑥3
, maka kita memperoleh bentuk kuadrat
𝑋 𝑇 𝐴𝐴 = 𝑎11 𝑥1
2
+ 𝑎22 𝑥2
2
+ 𝑎33
2
𝑥3
2
+ 2𝑎12 𝑥1 𝑥2 + 2𝑎13 𝑥1 𝑥3 + 2𝑎23 𝑥2 𝑥3
Suku-suku hasil kali silang dari bentuk kuadrat ini dapat dihilangkan
dengan memisalkan 𝑋 = 𝐵𝐵 di mana U suatu vector kolom dengan
unsure-unsur 𝑢1, 𝑢2, 𝑢3 dan B suatu matriks orthogonal yang membuat
diagonal matriks A. bentuk kuadrat baru dalam 𝑢1, 𝑢2, 𝑢3 tanpa suku-
suku hasil kali silang dinamakan bentuk kanonik.
