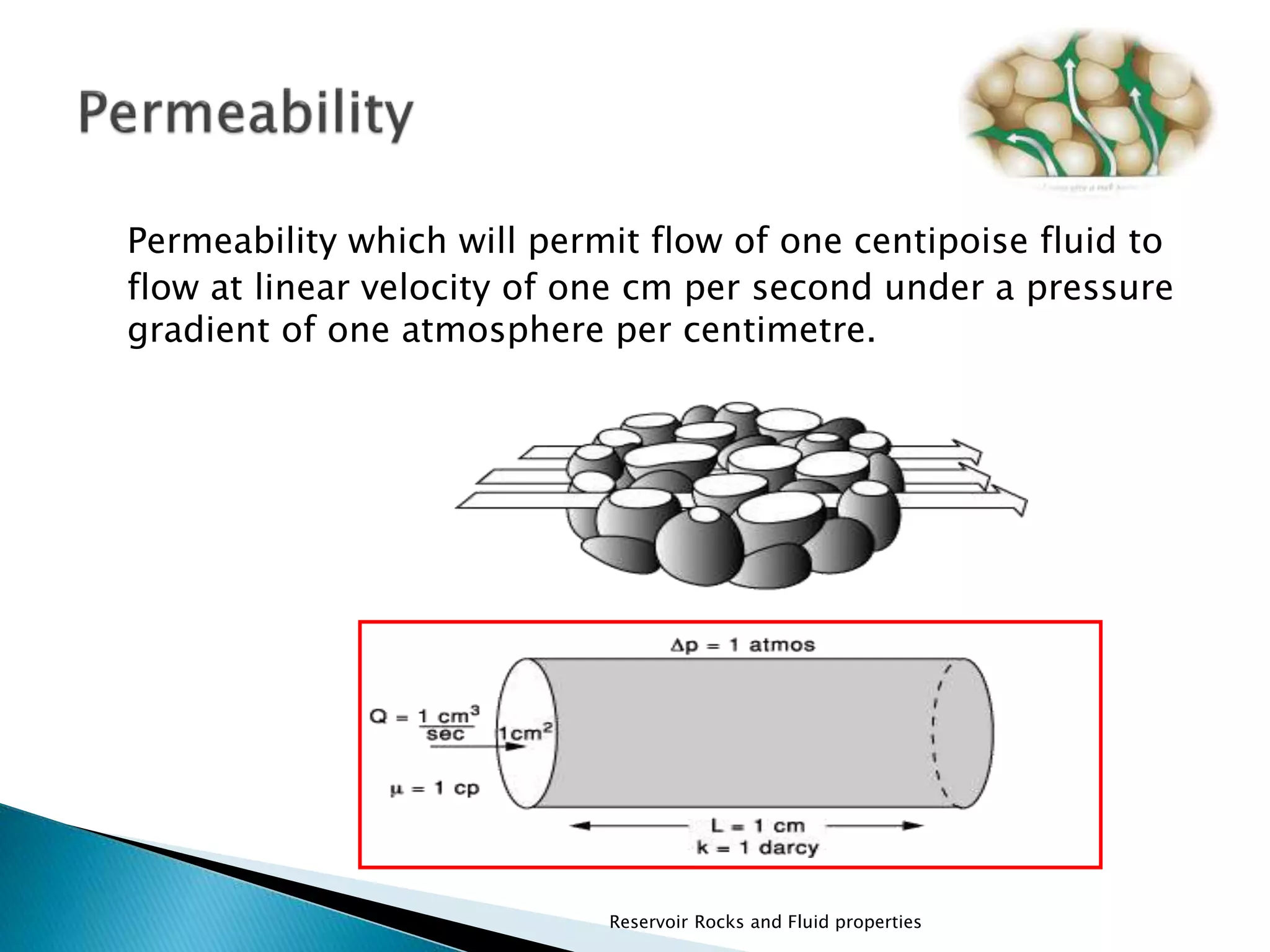
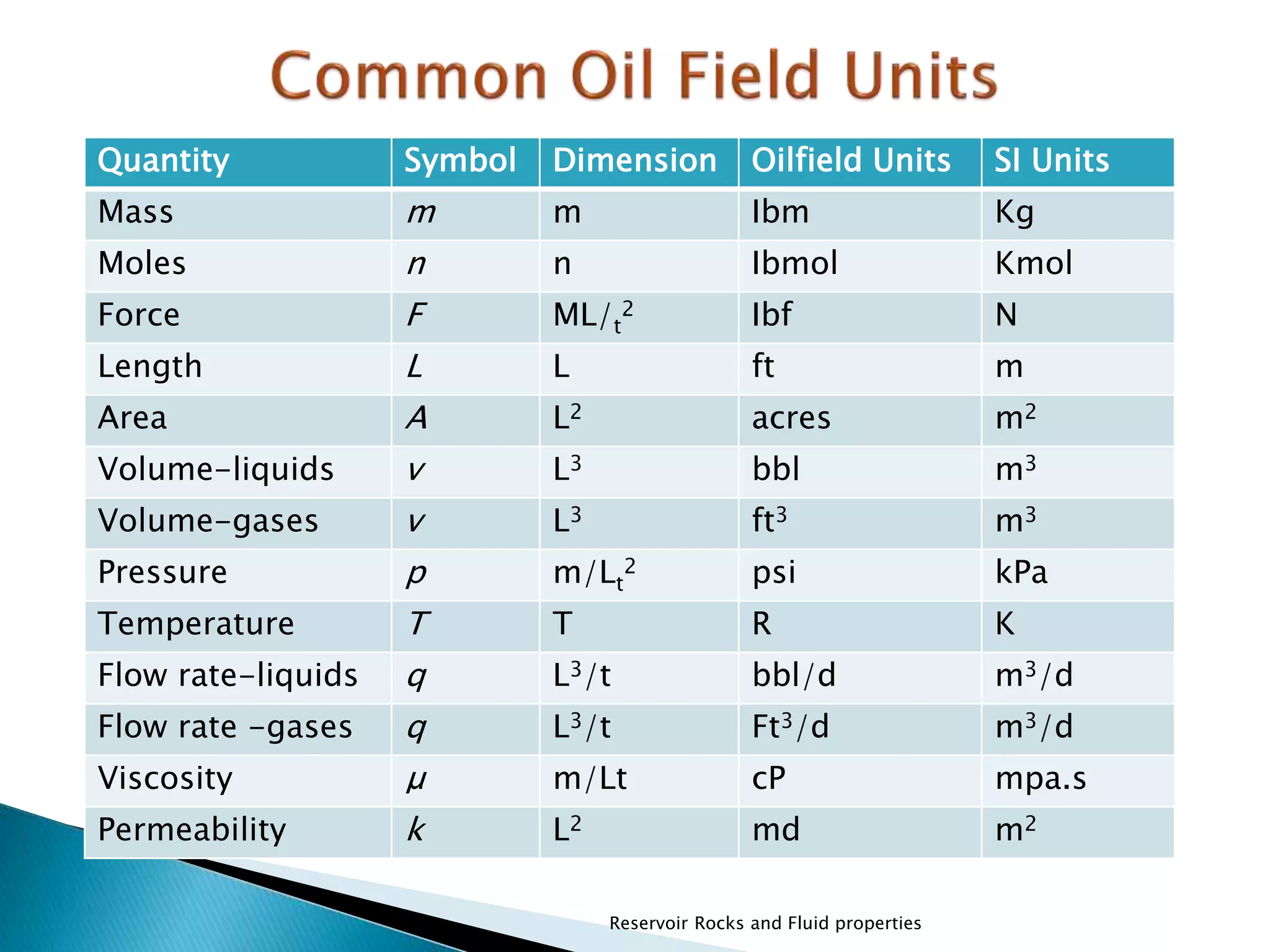
- Permeability is a property of porous rocks that measures their ability to transmit fluids. Higher permeability means fluids can flow more easily through the rock. - Darcy's law states that for laminar flow through a permeable medium, the flow rate is proportional to the permeability of the medium and the pressure gradient, and inversely proportional to the fluid viscosity. - There are different units used to measure and describe permeability, including darcies and millidarcies. Permeability is a key parameter in evaluating reservoir performance and fluid flow.

2.  Definition (ABW, Ref: API 27)
◦ … permeability is a property of the porous
medium and is a measure of the capacity of the
medium to transmit fluids
◦ … permeability is the fluid conductance capacity
of a rock, or it’s the a measure of the ease with
which the rock will permit the passage of fluids.
Reservoir Rocks and Fluid properties

3.  Permeability theory
 Permeability is an INTENSIVE property of a porous
medium (e.g. reservoir rock)
Reservoir Rocks and Fluid
properties

4. Permeability which will permit flow of one centipoise fluid to
flow at linear velocity of one cm per second under a pressure
gradient of one atmosphere per centimetre.
Reservoir Rocks and Fluid properties

5.  Three types of permeability
 Absolute permeability - the permeability of a porous medium
with only one fluid present (single-phase flow).
 When two or more fluids are present permeability of the rock to a
flowing fluid is called effective permeability (ko, kg, kw).
 Relative permeability is the ratio of absolute and effective
permeabilities kro=ko/k, krg=kg/k, krw=kw/k.
Reservoir Rocks and Fluid properties

6.  A French hydrologist named Darcy did the first work on
permeability. He was concerned about flow of water through
filters. He found that flow rate Q, is proportional to area of flow
A,h, and 1/L. This is expressed mathematically as flows:
1
h h
Q KA 1 2 

L
 Darcy’s “K” was determined to be a combination of
◦ k, permeability of the sand pack (porous medium, e.g.
reservoir rock)
◦ K is a constant of proportionality
◦ , viscosity of the liquid
 K constant may be written as;
2
Reservoir Rocks and Fluid properties
k
μ
K 

7.  Alternatively, eqn.1; can also be expressed in terms of the
pressure gradient dp over a section dL as;
3
dp
Where dp = Δhρg 4
– dp is the diff. b/w the upstream & downstream pressures
 Δh the diff. b/w the upstream and downstream hydraulic
gradients
 ρ fluid density
 g is the acceleration due to gravity (9.81 m/sec2)
Reservoir Rocks and Fluid
properties
dL
Q  KA

8. Darcy’s
Apparatus for
Determining
Permeability
h h
1 2

Q A
volumetric flow rate
cross sectional area


& hydraulic head at inlet and outlet
(Sand Pack Length) L
Reservoir Rocks and Fluid properties
length of the porous medium
Q
A
L
1 2



h h
L
Q

h1-h2
h1
h2
q
A
q
A

9. • Darcy did not consider the fluid viscosity.
• Restricted to a medium with 100% saturated by water
• Other researchers discovered that Q is inversely proportional to
Reservoir Rocks and Fluid properties
viscosity.

10. Extension of Darcy’s Equation
 Assumptions Used in Darcy Equation:
1. Steady state flow, under laminar regime i.e. Qin = Qout
2. Viscous flow - rate of flow directly proportional to pressure
gradient
3. The flowing fluid is incompressible.
4. Porous media 100% saturated with fluid which flowed
5. Fluid and porous media not reacting
Reservoir Rocks and Fluid properties

11.  Darcy’s Law can be extended to other fluids, if K is expressed as a
ratio of /μ, where μ is the viscosity of a given fluid and  the
permeability of the porous medium.
 Eqn. 3 can be written to account for viscosity μ as;
k
dp
Q = - A 5
Eqn.5 can be integrated b/w the limits of length from 0 to L and
pressure from P1(upstream) to P2 (downstream), for a fluid flow
case.
Reservoir Rocks and Fluid properties

dL

12.  Therefore,
6
7
KA 
P
or 8
Q L
Q
 0   
KA
Q  
Q
Hence, the original equation of Darcy was modified to account for
viscosity as follows:
9
KA
Q  
Reservoir Rocks and Fluid properties
   
p
p
dp
k
dL
A
2
1
0 
 k
L
 p p  A
2 1

  1 2 p p
L
 
L

  1 2 p p
L


13.  Permeability is determined by:
 Core analysis
 Well test analysis (flow testing)
◦ RFT (repeat formation tester) provides small well tests
 Production data
◦ production logging measures fluid flow into well
 Log data
◦ MRI (magnetic resonance imaging) logs calibrated via core analysis
Reservoir Rocks and Fluid properties

14. • Shape and size of pore system
• Sorting
• Cementation
• Fracturing and solution
• Lithology or rock type
Reservoir Rocks and Fluid properties

15.  Two sets of units are generally used in reservoir engineering:
Darcy units and Oil-field units
 For the purpose of the mathematical derivations, a system of
units commonly referred to as Darcy units are used. These
units are:
 Vs= cm/sec; μ = cP; ρ = gm/cc
 K = Darcy; g = cm/sec2; dp/ds = atm/cm
 For application to field data of the various mathematical
expressions, the second system of units called the practical
oil-field units are used.
Reservoir Rocks and Fluid properties

16.  From dimensional analysis, the dimension for K is [L]2.
We could use ft2, ins2, or cm2 for measure of permeability, but
these units are all too large to be applied in porous media.
 So Darcy unit is used and recommended , but in many cases the
millidarcy (mD)
 1 Darcy = 1000 miliDarcy
 1 Darcy ~ 10-8 sm2 (10-6 mm2)
 1 miliDarcy ~ 10-11 sm2 (10-9 mm2)
Reservoir Rocks and Fluid properties

17. Darcy’s Law - Darcy Units
 Linear (1-D) flow of an incompressible fluid
kA
μ L
q 
◦ where,
Δp
 q cm3/s
 k darcies
 A cm2
 p atm
  cp
 L cm
◦ The Darcy a derived unit of permeability, defined to make this
equation coherent (in Darcy units)

18. Darcy’s Law - Oilfield Units
 Linear (1-D) flow of an incompressible fluid
CkA
μ L
q 
◦ where,
Δp
 q bbl/D
 k millidarcies
 A ft2
 p psia
  cp
 L ft

19. Quantity Symbol Dimension Oilfield Units SI Units
Mass m m Ibm Kg
Moles n n Ibmol Kmol
Force F ML/2 Ibf N
t
Length L L ft m
Area A L2 acres m2
Volume-liquids v L3 bbl m3
Volume-gases v L3 ft3 m3
Pressure p m/Lt
2 psi kPa
Temperature T T R K
Flow rate-liquids q L3/t bbl/d m3/d
Flow rate -gases q L3/t Ft3/d m3/d
Viscosity μ m/Lt cP mpa.s
Permeability k L2 md m2
Reservoir Rocks and Fluid properties

20.  Permeability is an important parameter that controls the
reservoir performance. Its importance is reflected by the
number of available techniques typically used to estimate it.
 These different techniques provide formation permeability
that represents different averaging volumes.
 The quality of the reservoir, as it relates to permeability can
be classified as follows
< 10 md fair
10 – 100 High
100 – 1000 Very High
>1000 Exceptional
 This scale changes with time, for example 30 years ago k<
50 was considered poor.
Reservoir Rocks and Fluid properties

21.  What is 1 Darcy?
 A porous medium has a permeability of one Darcy, when a
single-phase fluid of one centipoises viscosity, that completely
fills the voids of the medium will flow through it, under
conditions of viscous flow (also known as laminar flow), at a
rate of one cubic centimeter cross sectional area, and under a
pressure or equivalent hydraulic gradient of one atmosphere
per centimeter.
Reservoir Rocks and Fluid properties

22.  Important Characteristics that must be considered in the
reservoir:
 Types of fluids in the reservoir
 Flow regimes
 Reservoir geometry
 Number of fluid flowing in the reservoir
Reservoir Rocks and Fluid properties

23.  Types of Fluids
• Incompressible fluids
• Slightly compressible fluids
• Compressible fluids
 Flow Regimes
• Steady state flow
• Unsteady state flow
• Pseudosteady state flow
Reservoir Rocks and Fluid properties

24.  Reservoir Geometry
• Linear flow
• Radial flow
• spherical and hemispherical flow
 Number of fluid flowing
• Single phase flow
• Two phase flow
• Three phase or multiple phase flow
Reservoir Rocks and Fluid properties

25.  Types of Fluids
• Incompressible fluids
• Slightly compressible fluids
• Compressible fluids
Reservoir Rocks and Fluid properties

26.  Flow Regimes
• Steady state flow
• Unsteady state flow
• Pseudosteady state flow
Reservoir Rocks and Fluid
properties

27.  Reservoir Geometry
• Linear flow
• Radial flow
• spherical and hemispherical flow
Reservoir Rocks and Fluid properties

28.  Steady state flow, i.e. Qin = Qout
 Viscous or Laminar flow: the particles flow in parallel paths
 Rock is 100% saturated with one fluid
 Fluid does not react with the; this a problem with shaly-sand
(interstitial particles)
 The formation is homogeneous and isotropic: same porosity,
same permeability and same fluid properties
Reservoir Rocks and Fluid properties

29.  Generalized form of Darcy’s Law
 The generalized Darcy’s law is given by the following equation:
k 
dp
Vs
 

 Vs = Q/A and dp/ds = dp/dx, hence



KA dp
Reservoir Rocks and Fluid properties
 
ds






 
dx
Q

Separating the variables and
integrating gives the following eqn.:
Note that P1>P2

30.    
 
  
0
6
k dP

k dP
k dP
Q
g dz
 
 


 0
    
2 1 1 2 *10
1.0135
2
1
P P
k
P P
k
L
Q
Q
Q
Q
A
dP
k
dx
A
dP
k
dx
A
dx
A
dx
v
ds
ds
v
A
P
P
L
x
s
     




 
 





• Fluid not compressed (no density
change with pressure)
• Steady flow (mass in = mass out)
• In horizontal flow (Linear):
dP
dx
dP
ds
dz
ds
 0 ,  
 
kA P P
Q 1 2 
 
L


31. The generalized form of Darcy’s Law includes pressure and gravity
terms to account for horizontal or non-horizontal flow



k dp
g s
q
   
dz


dΦ
k
Reservoir Rocks and Fluid properties



ds
ds
A
v
c
s


 The gravity term has dimension of pressure / length
Flow potential includes both pressure and gravity terms, simplifying
Darcy’s Law




q
  
ds
μ
A
vs
 = p - gZ/c; Z+; Z is elevation measured from a datum
 has dimension of pressure

32.  The gravitational conversion constant, c, is needed to convert
the gravity term to units of pressure gradient
[pressure/length]
 A clear way to determine the sign of the gravity term (+ or -)
is to consider the static case. If no fluid is flowing, then there
is no potential gradient (potential is constant), while pressure
changes with elevation, due to fluid density (dp=(g/c)dZ).
Reservoir Rocks and Fluid properties

33. Reservoir Rocks and Fluid properties

34. Reservoir Rocks and Fluid properties

35.  Fluid not compressed
Q
 
Q
 Steady flow (stream mass was constant)
rw
re
Pwf Pe
h
r
  
P
r
w
w
   
 
 
e w

 
 
r
hk P P
e w
r
e
w
e
w
P
P
r
r
r
Q
Q
P P
k
r
h
P
k
r
h
PdP
k
dr
h r
e
w
e
w
ln
ln
2
2
ln
2
1
2


 



36.  Q = flow rate, m3/sec
 K = permeability, m2
 h = thickness, m
 Pe = pressure drainage radius, N/m2
 Pwf = flowing pressure, N/m2
 = fluid viscosity, N/m2
 re = drainage radius, m
 rw = the well-bore radius, m
Reservoir Rocks and Fluid properties


37. • Permeability varies across several
horizontal layers (k1,k2,k3)
◦ Discrete changes in permeability
    1 2 3 i h h h h h
◦ Same pressure drop for each layer
1 2 1 2 3 p - p  Δp  Δp  Δp  Δp
◦ Total flow rate is summation of flow rate for all layers
    1 2 3 i q q q q q
◦ Average permeability results in correct total flow rate
q  
Δp ; A w h
kwh
μ L

38. • Substituting,
kwh
q 1 1 2 2 3 3    
• Rearranging,
k wh
 k  h
k 
i i
h
k wh
k wh
• Average permeability reflects flow capacity of all layers
Δp
μ L
Δp
μ L
Δp
μ L
Δp
μ L

39. • Permeability varies across several
vertical layers (k1,k2,k3)
◦ Discrete changes in permeability
    1 2 3 i L L L L L
◦ Same flow rate passes through each layer
1 2 3 q  q  q  q
◦ Total pressure drop is summation of pressure drop across
layers
     1 2 1 2 3 i p p Δp Δp Δp Δp
◦ Average permeability results in correct total pressure drop
p - p1 2   
; A w h
qμ L
kwh

40. qμ L
k wh
qμ L
k wh
qμ L
k wh
• Substituting,
qμ L
kwh
p - p
3
3
2
2
1
1
1 2    
• Rearranging,
k
• If k1>k2>k3, then
L


L
i
k
i
– Linear pressure profile in each layer
0 L
x 
p 
p1
p2
0
k

41. • Permeability varies across several
(3) horizontal layers (k1,k2,k3)
◦ Discrete changes in permeability
    1 2 3 i h h h h h
◦ Same pressure drop for each layer
e w 1 2 3 p - p  Δp  Δp  Δp  Δp
◦ Total flow rate is summation of flow rate for all layers
    1 2 3 i q q q q q
◦ Average permeability results in correct total flow rate
Δp
2π k h
μ ln(r /r )
q
e w


42. • Substituting (rw=r1, r2 ,re=r3),
qμ ln(r /r )
e w   
• Rearranging,
e w 2 w
ln(r /r )
e w
qμ ln(r /r )
(ln(r /r )
 

i 1 i
k
All Layers i
k
qμ ln(r /r )
e 2
2π k h
2π k h
2π k h
p - p
2
1

43. It is necessary to determine an average value of permeability.
Three common types of computed averages are as follows:
Reservoir Rocks and Fluid properties
i) arithmetic average
ii) harmonic average
ii) geometric average
Selection of the averaging technique should be based primarily on
the geometry of the flow system.

44. Reservoir Rocks and Fluid properties
k1
k2
k3
h1
h2
h3
 
k h
A h

i i
i
k
Q
Parallel Flow
Arithmetic Average

45. L
H L k
Series Flow
k1 k2 k3 
Reservoir Rocks and Fluid properties
L1 L2 L3
 
i
i i
k
/
 Harmonic Average

46. 1
Random Flow
Geometric Average
  h h h  hi
G k k k k
1 2 3 ....... 1 2 3
Reservoir Rocks and Fluid properties

47. Reservoir Rocks and Fluid properties