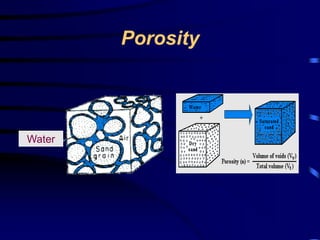
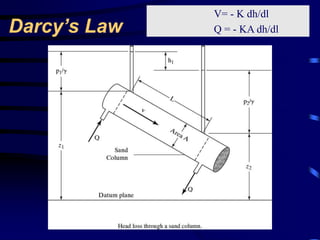
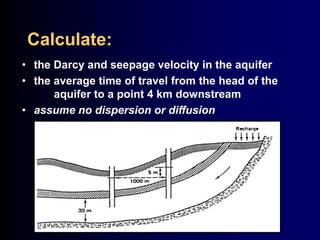
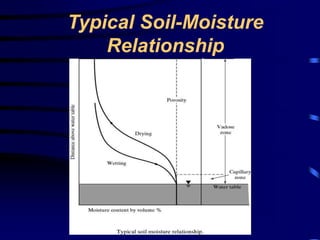
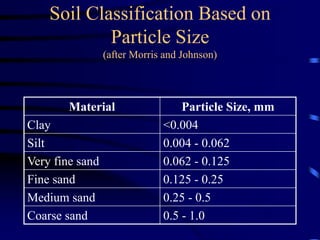
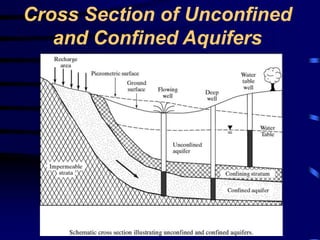
This document provides an overview of groundwater hydrology and aquifer systems. It discusses key topics such as: - Aquifer parameters like porosity, hydraulic conductivity, and storage coefficients. - Governing equations for groundwater flow including Darcy's Law and the Dupuit equation for unconfined flow. - Vertical zones of subsurface water and soil moisture relationships. - Characteristics of confined and unconfined aquifers. 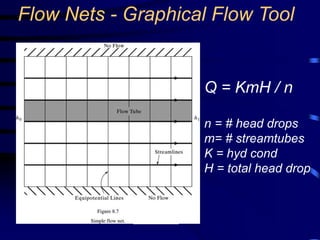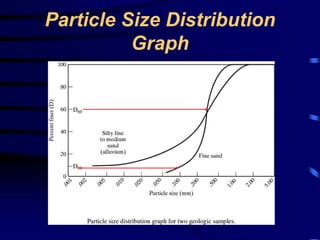- Flow nets as a graphical tool for analyzing groundwater flow patterns. The document serves as an introduction to analyzing groundwater resources and flow using fundamental hydrogeological principles.

1. Ground Water Hydrology
Introduction - 2005
Philip B. Bedient
Civil & Environmental Engineering
Rice University

2. GW Resources - Quantity
• Aquifer system parameters
• Rate and direction of GW flow
• Darcy’s Law - governing flow relation
• Dupuit Eqn for unconfined flow
• Recharge and discharge zones
• Well mechanics- pumping for water supply,
hydraulic control, or injection of wastes

3. GW Resources - Quality
• Contamination sources
• Contaminant transport mechanims
• Rate and direction of GW migration
• Fate processes-chemical, biological
• Remediation Systems for cleanup

4. Trends in Ground Water Use

5. Ground Water: A Valuable
Resource
• Ground water supplies 95% of the drinking
water needs in rural areas.
• 75% of public water systems rely on
groundwater.
• In the United States, ground water provides
drinking water to approximately 140 million
people.
• Supplies about 40% of Houston area

6. Regional Aquifer Issues

7. Typical Hydrocarbon Spill

8. Aquifer Characteristics
1. Matrix type
2. Porosity (n)
3. Confined or unconfined
4. Vertical distribution (stratigraphy or layering)
5. Hydraulic conductivity (K)
6. Intrinsic permeability (k)
7. Transmissivity (T)
8. Storage coefficient or Storativity (S)

9. Vertical Distribution of
Ground Water

10. Vertical Zones of Subsurface
Water
• Soil water zone: extends from the ground surface
down through the major root zone, varies with soil
type and vegetation but is usually a few feet in
thickness
• Vadose zone (unsaturated zone): extends from the
surface to the water table through the root zone,
intermediate zone, and the capillary zone
• Capillary zone: extends from the water table up to
the limit of capillary rise, which varies inversely
with the pore size of the soil and directly with the
surface tension

11. Typical Soil-Moisture
Relationship

12. Soil-Moisture Relationship
• The amount of moisture in the vadose zone
generally decreases with vertical distance
above the water table
• Soil moisture curves vary with soil type and
with the wetting cycle

13. Vertical Zones of Subsurface
Water Continued
• Water table: the level to which water will rise in a
well drilled into the saturated zone
• Saturated zone: occurs beneath the water table
where porosity is a direct measure of the water
contained per unit volume

14. Porosity
– Porosity averages about 25% to 35% for most
aquifer systems
– Expressed as the ratio of the volume of voids Vv to
the total volume V:
n = Vv/V = 1- b/m
where:
b is the bulk density, and
m is the density of grains

15. Porosity
Water

16. Arrangement of Particles in a
Subsurface Matrix
Porosity depends on:
• particle size
• particle packing
• Cubic packing of spheres with a theoretical
porosity of 47.65%

17. • Rhombohedral packing of spheres with a
theoretical porosity of 25.95%

18. Soil Classification Based on
Particle Size
(after Morris and Johnson)
Material Particle Size, mm
Clay <0.004
Silt 0.004 - 0.062
Very fine sand 0.062 - 0.125
Fine sand 0.125 - 0.25
Medium sand 0.25 - 0.5
Coarse sand 0.5 - 1.0

19. Soil Classification…cont.
Material Particle Size, mm
Very coarse sand 1.0 - 2.0
Very fine gravel 2.0 - 4.0
Fine gravel 4.0 - 8.0
Medium gravel 8.0 - 16.0
Coarse gravel 16.0 - 32.0
Very coarse gravel 32.0 - 64.0

20. Particle Size Distribution
Graph

21. Particle Size Distribution
and Uniformity
• The uniformity
coefficient U indicates
the relative sorting of
the material and is
defined as D60/D10
U is a low value for
fine sand compared
to alluvium which is
made up of a range
of particle sizes

22. Cross Section of Unconfined
and Confined Aquifers

23. Unconfined Aquifer Systems
• Unconfined aquifer: an aquifer where the
water table exists under atmospheric
pressure as defined by levels in shallow
wells
• Water table: the level to which water will
rise in a well drilled into the saturated zone

24. Confined Aquifer Systems
• Confined aquifer: an aquifer that is overlain
by a relatively impermeable unit such that
the aquifer is under pressure and the water
level rises above the confined unit
• Potentiometric surface: in a confined
aquifer, the hydrostatic pressure level of
water in the aquifer, defined by the water
level that occurs in a lined penetrating well

25. Special Aquifer Systems
• Leaky confined aquifer: represents a stratum that
allows water to flow from above through a leaky
confining zone into the underlying aquifer
• Perched aquifer: occurs when an unconfined water
zone sits on top of a clay lens, separated from the
main aquifer below

26. Ground Water Flow
Darcy’s Law
Continuity Equation
Dupuit Equation

27. Darcy’s Law
• Darcy investigated the flow of water through beds of
permeable sand and found that the flow rate through
porous media is proportional to the head loss and
inversely proportional to the length of the flow path
• Darcy derived equation of governing ground water
flow and defined hydraulic conductivity K:
V = Q/A
where:
A is the cross-sectional area
V  -Δh, and
V  1/ΔL

28. Darcy’s Law
V= - K dh/dl
Q = - KA dh/dl

29. Example of Darcy’s Law
• A confined aquifer has a source of recharge.
• K for the aquifer is 50 m/day, and n is 0.2.
• The piezometric head in two wells 1000 m apart is
55 m and 50 m respectively, from a common
datum.
• The average thickness of the aquifer is 30 m,
• The average width of flow is 5 km.

30. Calculate:
• the Darcy and seepage velocity in the aquifer
• the average time of travel from the head of the
aquifer to a point 4 km downstream
• assume no dispersion or diffusion

31. The solution
• Cross-Sectional area
30(5)(1000) = 15 x 104 m2
• Hydraulic gradient
(55-50)/1000 = 5 x 10-3
• Rate of Flow through aquifer
Q = (50 m/day) (75 x 101 m2)
= 37,500 m3/day
• Darcy Velocity:
V = Q/A = (37,500m3/day) / (15
x 104 m2) = 0.25m/day

32. Therefore:
• Seepage Velocity:
Vs = V/n = 0.25 / 0.2 =
1.25 m/day (about 4.1 ft/day)
• Time to travel 4 km downstream:
T = 4(1000m) / (1.25m/day) =
3200 days or 8.77 years
• This example shows that water moves
very slowly underground.

33. Ground Water Hydraulics
• Hydraulic conductivity, K, is an indication
of an aquifer’s ability to transmit water
–Typical values:
10-2 to 10-3 cm/sec for Sands
10-4 to 10-5 cm/sec for Silts
10-7 to 10-9 cm/sec for Clays

34. Ground Water Hydraulics
Transmissivity (T) of Confined Aquifer
-The product of K and the saturated
thickness of the aquifer T = Kb
- Expressed in m2/day or ft2/day
- Major parameter of concern
- Measured thru a number of
tests - pump, slug, tracer

35. Ground Water Hydraulics
Intrinsic permeability (k)
Property of the medium only, independent of
fluid properties
Can be related to K by:
K = k(g/μ)
where: μ = dynamic viscosity
 = fluid density
g = gravitational constant

36. Storage Coefficient
Relates to the water-yielding capacity of an aquifer
S = Vol/ (AsH)
– It is defined as the volume of water that an aquifer
releases from or takes into storage per unit surface
area per unit change in piezometric head - used
extensively in pump tests.
• For confined aquifers, S values range between
0.00005 to 0.005
• For unconfined aquifers, S values range
between 0.07 and 0.25, roughly equal to the
specific yield

37. Regional Aquifer Flows are
Affected by Pump Centers
Streamlines and Equipotential lines

38. Derivation of the Dupuit
Equation - Unconfined Flow

39. Dupuit Assumptions
For unconfined ground water flow Dupuit
developed a theory that allows for a simple
solution based off the following assumptions:
1) The water table or free surface is only
slightly inclined
2) Streamlines may be considered horizontal
and equipotential lines, vertical
3) Slopes of the free surface and hydraulic
gradient are equal

40. Derivation of the Dupuit
Equation
Darcy’s law gives one-dimensional flow per unit
width as:
q = -Kh dh/dx
At steady state, the rate of change of q with
distance is zero, or
d/dx(-Kh dh/dx) = 0
OR (-K/2) d2h2/dx2 = 0
Which implies that,
d2h2/dx2 = 0

41. Dupuit Equation
Integration of d2h2/dx2 = 0 yields
h2 = ax + b
Where a and b are constants. Setting the boundary
condition h = ho at x = 0, we can solve for b
b = ho
2
Differentiation of h2 = ax + b allows us to solve for a,
a = 2h dh/dx
And from Darcy’s law,
hdh/dx = -q/K

42. Dupuit Equation
So, by substitution
h2 = h0
2 – 2qx/K
2 = h0
Setting h = hL
2 – 2qL/K
Rearrangement gives
2- hL
q = K/2L (h0
2) Dupuit Equation
Then the general equation for the shape of the parabola is
h2 = h0
2 – x/L(h0
2- hL
2) Dupuit Parabola
However, this example does not consider recharge to the aquifer.

43. Cross Section of Flow
q

44. Adding Recharge W -
Causes a Mound to Form
Divide

45. Dupuit Example
Example:
2 rivers 1000 m apart
K is 0.5 m/day
average rainfall is 15 cm/yr
evaporation is 10 cm/yr
water elevation in river 1 is 20 m
water elevation in river 2 is 18 m
Determine the daily discharge per meter width into each
River.

46. Example
Dupuit equation with recharge becomes
h2 = h0
2 + (hL
2 - h0
2) + W(x - L/2)
If W = 0, this equation will reduce to the parabolic
Equation found in the previous example, and
q = K/2L (h0
2- hL
2) + W(x-L/2)
Given:
L = 1000 m
K = 0.5 m/day
h0 = 20 m
hL= 28 m
W = 5 cm/yr = 1.369 x 10-4 m/day

47. Example
For discharge into River 1, set x = 0 m
q = K/2L (h0
2- hL
2) + W(0-L/2)
= [(0.5 m/day)/(2)(1000 m)] (202 m2 – 18 m2 ) +
(1.369 x 10-4 m/day)(-1000 m / 2)
q = – 0.05 m2 /day
The negative sign indicates that flow is in the opposite direction
From the x direction. Therefore,
q = 0.05 m2 /day into river 1

48. Example
For discharge into River 2, set x = L = 1000 m:
q = K/2L (h0
2- hL
2) + W(L-L/2)
= [(0.5 m/day)/(2)(1000 m)] (202 m2 – 18 m2 ) +
(1.369 x 10-4 m/day)(1000 m –(1000 m / 2))
q = 0.087 m2/day into River 2
By setting q = 0 at the divide and solving for xd, the
water divide is located 361.2 m from the edge of
River 1 and is 20.9 m high

49. Flow Nets - Graphical Flow Tool
Q = KmH / n
n = # head drops
m= # streamtubes
K = hyd cond
H = total head drop

50. Flow Net in Isotropic Soil
Portion of a flow net is shown below
Y
F
Curvilinear Squares

51. Flow Net Theory
1. Streamlines Y and Equip. lines  are .
2. Streamlines Y are parallel to no flow
boundaries.
3. Grids are curvilinear squares, where
diagonals cross at right angles.
4. Each stream tube carries the same flow.

52. Seepage Flow under a Dam