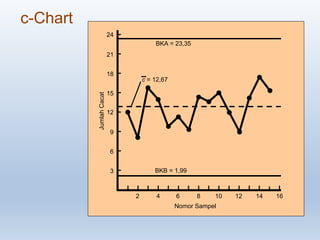
Dokumen ini membahas pengendalian proses statistik (SPC) yang meliputi penggunaan diagram kontrol untuk memantau dan meningkatkan kualitas proses produksi dan layanan. Ditekankan pentingnya pengukuran statistik dasar seperti rata-rata, varians, dan deviasi standar, serta cara menerapkan SPC dalam berbagai sektor seperti pelayanan kesehatan dan ritel. Selain itu, dijelaskan secara detail tentang penggunaan p-chart dan c-chart untuk analisis atribut, serta x-bar chart dan r-chart untuk variabel dalam memastikan proses tetap terkontrol.

1. Pengendalian Proses Statistik
Dodi Mulyadi, MT

2. • Pengendalian Proses Statistik
• Statistik Dasar
• Diagram Kontrol
• Diagram Kontrol untuk Atribut
• Diagram Kontrol untuk Variabel
• Pola Bagan Kontrol
• SPC dengan Excel dan OM Tools
• Kemampuan Proses

3. Pengendalian Proses Statistik (SPC)
• Pengendalian Proses Statistik
• memantau proses produksi
untuk mendeteksi dan
mencegah kualitas yang buruk
• Sampel
• sebagian jumlah produk yang
digunakan untuk proses inspeksi
• Diagram Kontrol
• Proses produksi harus berada
dalam batas kontrol statistik
BKA
BKB

4. Variabilitas Proses
• Acak
• melekat dalam sebuah
proses
• tergantung pada
peralatan dan mesin,
teknik, operator, dan
sistem pengukuran
• kejadian “natural”
• Tidak Acak
• penyebab khusus
• dapat diidentifikasi dan
diperbaiki
• termasuk peralatan yang
tidak disesuaikan, bahan
rusak, perubahan suku
cadang atau bahan,
mesin atau peralatan
yang rusak, kelelahan
operator atau metode
kerja yang buruk, atau
kesalahan karena
kurangnya pelatihan.

5. SPC dalam Manajemen Mutu
• Fungsi Menggunakan SPC
• Apakah proses terkontrol?
• Identifikasi masalah untuk melakukan
perbaikan
• Berkontribusi pada tujuan TQM untuk terus
melakukan perbaikan

6. Ukuran Mutu:
Atribut dan Variabel
• Atribut
• Karakteristik yang dievaluasi dengan respon
diskrit
• baik / buruk; ya / tidak; benar / salah
• Ukuran variabel
• Karakteristik yang kontinu dan bisa diukur
• Berat, panjang, tegangan, volume

7. SPC untuk Jasa Pelayan
• Sifat cacat (defect) berbeda dalam pelayanan
jasa
• Service defect adalah kegagalan untuk
memenuhi kebutuhan pelanggan
• Memantau waktu pelayanan dan kepuasan
pelanggan

8. SPC untuk Jasa Pelayan
• Rumah sakit
• ketepatan waktu & kecepatan perawatan, tanggapan staf
terhadap permintaan, akurasi tes laboratorium, kebersihan,
kesopanan, keakuratan dokumen, kecepatan administrasi
masuk & keluar rawat inap
• Toko grosir
• Waktu tunggu untuk pembayaran di kasir, frekuensi kontrol
stok barang, kualitas makanan, kebersihan, keluhan
pelanggan
• Penerbangan
• penundaan penerbangan, penanganan bagasi & bagasi
yang hilang, waktu tunggu di loket tiket & check-in,
kesopanan agen & petugas pramugari, informasi
penerbangan yang akurat, kebersihan kabin & perawatan

9. SPC untuk Jasa Pelayan
• Restoran cepat saji
• waktu tunggu untuk layanan, keluhan pelanggan,
kebersihan, kualitas makanan, ketertiban, sopan santun
karyawan
• Penjualan melalui katalog
• ketepatan pesanan, pengetahuan operator & kesopanan,
pengemasan, waktu pengiriman, waktu tunggu pesanan
melalui telepon
• Perusahaan asuransi
• akurasi penagihan, ketepatan waktu pemrosesan klaim,
ketersediaan agen & waktu respon

10. Statistik Dasar
• Mean atau titik tengah atau biasa disebut rata-
rata
• adalah jumlah data dibagi banyak data
• Contoh: hasil pengukuran panjang (mm): 25,06;
25,03; 25.08; 25,05; 25,03
n
x
n
i
ix
 1
05,25
5
25,125
5
03,2505,2508,2503,2506,25




x
x
x

11. Statistik Dasar
• Range atau rentang atau jangkauan
• adalah selisih antara data dengan nilai yang terbesar
dengan data denga nilai yang terkecil
• Contoh: hasil pengukuran panjang (mm): 25,06;
25,03; 25,08; 25,05; 25,03
05,003,2508,25
03,25
08,25
min
max



R
x
x
minmax xxR 

12. Statistik Dasar
• Variance atau varians atau ragam perbedaan
• adalah ukuran seberapa jauh sebuah kumpulan
bilangan tersebar. Varians nol mengindikasikan
bahwa semua nilai sama.
• atau
1
)(
1
2
2






n
xx
s
ni
i
1
1
2
12
2














n
n
x
x
s
ni
i
ni
i

13. Statistik Dasar
• Deviasi standar atau simpangan baku
• adalah rata-rata jarak penyimpangan titik-titik data
diukur dari nilai rata-rata data tersebut.
• deviasi standar sampel:
1
)(
1
2
2






n
xx
ss
ni
i

1
1
2
12
2














n
n
x
x
ss
ni
i
ni
i


14. Statistik Dasar
• Contoh varians dan deviasi standar
• Data hasil pengukuran panjang blok (mm):
25,6; 25,3; 25,8; 25,8; 25,5; 25,5; 25,3
• Langkah Pertama, buat tabel data
n x x2
1 25,6 655,36
2 25,3 640,09
3 25,8 665,64
4 25,8 665,64
5 25,5 650,25
6 25,5 650,25
7 25,3 640,09

15. Statistik Dasar
• Langkah Kedua, tentukan jumlah kolom x, jumlah kolom
x2 dan kuadrat dari jumlah kolom x
n x x2
1 25,6 655,36
2 25,3 640,09
3 25,8 665,64
4 25,8 665,64
5 25,5 650,25
6 25,5 650,25
7 25,3 640,09
(Σx) 178,8
(Σx)2 31969,44
(Σx2) 4567,32

16. Statistik Dasar
• Langkah Ketiga, hitung varians
(Σx) 178,8
(Σx)2 31969,44
(Σx2) 4567,32
1
1
2
12
2














n
n
x
x
s
ni
i
ni
i
043,0
17
7
44,31969
32,4567
2



s

17. Statistik Dasar
• Langkah Keempat, hitung deviasi standar
21,0043,02
 ss

18. Penggunaan Diagram Kontrol
• Proses
• Memiliki kecenderungan untuk lepas kontrol
• Sangat berbahaya dan mahal jika tidak terkendali
• Contoh:
• Pada awal proses, karena akan terjadi pemborosan jika
awal proses “buruk”
• Sebelum mencapai titik tidak bisa daur ulang atau mahal,
dimana setelah itu produk sulit untuk dikerjakan ulang
atau diperbaiki
• Sebelum dan sesudah proses perakitan atau pengecatan
yang mungkin terjadi cacat
• Sebelum produk atau jasa dikirim ke pelanggan

19. Diagram Kontrol
• Grafik yang memonitor kualitas proses
• Batas kontrol
• bagian atas dan bawah dari bagan kendali
• Bagan atribut
• p-chart
• c-chart
• Bagan variabel
• mean (x bar – chart)
• range (R-chart)

20. Bagan Kontrol Proses
1 2 3 4 5 6 7 8 9 10
Nomor Sampel
Batas
Kontrol
Atas
Proses
Rata-rata
Batas
Kontrol
Bawah
Keluar batas kontrol

21. Distribusi Normal
• Probabilitas, Z= 2.00 dan Z = 3.00
=0 1 2 3-1-2-3
95%
99.74%

22. Proses Terkontrol
1. Jika tidak ada titik sampel di luar batas
2. Sebagian besar sampel mendekati
proses rata-rata
3. Jumlah titik yang berada di atas dan di
bawah garis tengah adalah hampir sama
4. Distribusi titik poin mucul secara acak

23. Diagram Kontrol untuk Atribut
• p-chart
• menggunakan bagian (proporsi) yang cacat dalam
sampel
• c-chart
• menggunakan jumlah cacat (ketidaksesuaian)
dalam sampel

24. p-Chart
BKA = p + zp
BKB = p - zp
z = jumlah penyimpangan standar dari rata-rata proses
p = proporsi sampel rusak; perkiraan proses rata-rata
p = standar deviasi proporsi sampel
n = banyaknya produk dalam sub-grup
p =

25. p-Chart
20 sample dari 100 pasang jeans
Jumlah Proporsi
SAMPEL Produk Cacat Produk Cacat
1 6 0,06
2 0 0,00
3 4 0,04
: : :
: : :
20 18 0,18
200

26. p-Chart
BKA = p + z = 0,10 + 3
p(1 - p)
n
0,10(1 - 0,10)
100
BKA = 0,190
BKB = 0,010
BKB = p - z = 0,10 - 3
p(1 - p)
n
0,10(1 - 0,10)
100
= 200 / 20(100) = 0,10
total produk cacat
total produk dicek
p =

27. p-Chart
0,02
0,04
0,06
0,08
0,10
0,12
0,14
0,16
0,18
0,20
ProporsiProdukCacat
Nomor Sampel
2 4 6 8 10 12 14 16 18 20
BKA= 0,190
BKB= 0,010
p = 0,10

28. p-Chart dalam Excel / Spreadsheets

29. c-Chart
BKA = c + zc
BKB = c - zc
dimana
c = jumlah cacat per sampel
c = c

30. c-Chart
Jumlah cacat pada 15 grup sampel
1 12
2 8
3 16
: :
: :
15 15
190
c = = 12,67
190
15
BKA = c + zc
= 12,67 + 3 12,67
= 23,35
BKB = c - zc
= 12,67 - 3 12,67
= 1,99
JUMLAH
CACAT

31. c-Chart
3
6
9
12
15
18
21
24
JumlahCacat
Nomor Sampel
2 4 6 8 10 12 14 16
BKA = 23,35
BKB = 1,99
c = 12,67

32. Diagram Kontrol untuk Variabel
 Grafik Jangkauan ( R-Chart )
 Menggambarkan Jangkauan Sampel
(variabilitas)
 Bagan Rata-rata ( x -Chart )
 Menggambarkan Rata-rata Sampel

33. x-bar Chart:  Diketahui
BKA = x + z x
BKB = x - z x
-
-
=
=
Dimana
 = deviasi standar proses
x = deviasi standar dari rata-rata sample =/
k = jumlah sampel (subgroup)
n = ukuran sampel (jumlah yang diobservasi)
x1 + x2 + ... + xk
kX =
=
- - -
n

34. Observasi (Diameter Slip-Ring, cm) n
Sampel k 1 2 3 4 5
-
Contoh x-bar Chart:  Diketahui
x
Misal, diketahui σ = 0,08

35. Contoh x-bar Chart:  Diketahui
= 5,01 - 3(0,08 / )10
= 4,93
_____
10
50,09
= 5,01X =
=
BKB = x - z x
= -BKA = x + z x
=
-
= 5,01 + 3(0,08 / )10
= 5,09

36. x-bar Chart:  Tidak Diketahui
_
BKA = x + A2R
BKB = x - A2R
=
=
_
dimana
x = Rata-rata dari sampel rata-rata
R = Nilai jangkauan rata-rata
=
_

37. Faktor
Kontrol
n A2 D3 D4
2 1.880 0.000 3.267
3 1.023 0.000 2.575
4 0.729 0.000 2.282
5 0.577 0.000 2.114
6 0.483 0.000 2.004
7 0.419 0.076 1.924
8 0.373 0.136 1.864
9 0.337 0.184 1.816
10 0.308 0.223 1.777
11 0.285 0.256 1.744
12 0.266 0.283 1.717
13 0.249 0.307 1.693
14 0.235 0.328 1.672
15 0.223 0.347 1.653
16 0.212 0.363 1.637
17 0.203 0.378 1.622
18 0.194 0.391 1.609
19 0.187 0.404 1.596
20 0.180 0.415 1.585
21 0.173 0.425 1.575
22 0.167 0.435 1.565
23 0.162 0.443 1.557
24 0.157 0.452 1.548
25 0.153 0.459 1.541
Faktor R-chart
Sample
Size Faktor X-chart

38. Contoh x-bar Chart:  Tidak Diketahui
OBSERVASI (SLIP- RING DIAMETER, CM)
SAMPLE k 1 2 3 4 5 x R
1 5.02 5.01 4.94 4.99 4.96 4.98 0.08
2 5.01 5.03 5.07 4.95 4.96 5.00 0.12
3 4.99 5.00 4.93 4.92 4.99 4.97 0.08
4 5.03 4.91 5.01 4.98 4.89 4.96 0.14
5 4.95 4.92 5.03 5.05 5.01 4.99 0.13
6 4.97 5.06 5.06 4.96 5.03 5.01 0.10
7 5.05 5.01 5.10 4.96 4.99 5.02 0.14
8 5.09 5.10 5.00 4.99 5.08 5.05 0.11
9 5.14 5.10 4.99 5.08 5.09 5.08 0.15
10 5.01 4.98 5.08 5.07 4.99 5.03 0.10
50.09 1.15Total

39. Contoh x-bar Chart:  Tidak Diketahui
115.0
10
15.1

k
R
R
_
BKA = x + A2R
=
= 50.09
10
_____
x = = = 5.01 cm
x
k
___
= 5.01 + (0.58)(0.115) = 5.08
_
BKB = x - A2R
=
= 5.01 - (0.58)(0.115) = 4.94
_

40. Contoh
x- bar
Chart BKA = 5.08
BKB = 4.94
Rata-rata
Nomor Sampel
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
5.10 –
5.08 –
5.06 –
5.04 –
5.02 –
5.00 –
4.98 –
4.96 –
4.94 –
4.92 –
x = 5.01=

41. R- Chart
BKA = D4R BKB = D3R
R =
R
k'
dimana
R = jangkauan masing-masing sampel
k' = jumlah sampel sub kelompok

42. Contoh R-Chart
OBSERVATIONS (SLIP- RING DIAMETER, CM)
SAMPLE k 1 2 3 4 5 x R
1 5.02 5.01 4.94 4.99 4.96 4.98 0.08
2 5.01 5.03 5.07 4.95 4.96 5.00 0.12
3 4.99 5.00 4.93 4.92 4.99 4.97 0.08
4 5.03 4.91 5.01 4.98 4.89 4.96 0.14
5 4.95 4.92 5.03 5.05 5.01 4.99 0.13
6 4.97 5.06 5.06 4.96 5.03 5.01 0.10
7 5.05 5.01 5.10 4.96 4.99 5.02 0.14
8 5.09 5.10 5.00 4.99 5.08 5.05 0.11
9 5.14 5.10 4.99 5.08 5.09 5.08 0.15
10 5.01 4.98 5.08 5.07 4.99 5.03 0.10
50.09 1.15Totals

43. Contoh R-Chart
Faktor D3 and D4 diambil dari tabel
BKA = D4R = 2.11(0.115) = 0.243
BKB = D3R = 0(0.115) = 0
_
_

44. Contoh R-Chart
BKA = 0.243
BKB = 0
Jangkauan
Nomor Sampel
R = 0.115
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
0.28 –
0.24 –
0.20 –
0.16 –
0.12 –
0.08 –
0.04 –
0 –

45. X-bar and R charts – Excel & OM Tools

46. Menggunakan x-bar dan R-Charts
secara bersamaan
• Proses rata-rata dan variabilitas proses harus
terkontrol
• Sampel dapat memiliki rentang yang sangat
sempit, namun rata-rata sampel mungkin berada
di luar batas kontrol
• Atau, rata-rata sampel mungkin terkendali,
namun rentangnya mungkin tidak terkendali
• R-chart mungkin menunjukkan tren penurunan
yang berbeda

47. Pola Bagan Kontrol
• Run
• urutan nilai sampel yang menampilkan karakteristik
yang sama
• Tes Pola
• menentukan apakah pengamatan dalam batas-batas
diagram kontrol, menampilkan pola nonrandom

48. Pola Bagan Kontrol
BKA
BKB
Pengamatan sampel
konsisten di atas
garis tengah
BKB
BKA
Pengamatan sampel
konsisten di bawah
garis tengah

49. Pola Bagan Kontrol
BKB
BKA
Pengamatan sampel
terus meningkat
BKA
BKB
Pengamatan sampel
terus menurun

50. Zona untuk Tes Pola
BKA
BKB
Zona A
Zona B
ZonaC
Zona C
Zona B
Zona A
Rata-
rata
3 sigma = x + A2R
=
3 sigma = x - A2R
=
2 sigma = x + (A2R)
= 2
3
2 sigma = x - (A2R)
= 2
3
1 sigma = x + (A2R)
= 1
3
1 sigma = x - (A2R)
= 1
3
x
=
Nomor sample
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13

51. Melakukan Uji Pola
1 4.98 B — B
2 5.00 B N C
3 4.95 B T A
4 4.96 B T A
5 4.99 B N C
6 5.01 — N C
7 5.02 A N C
8 5.05 A N B
9 5.08 A N A
10 5.03 A T B
SAMPEL x ATAS/BAWAH NAIK/TURUN ZONA

52. Penentuan Ukuran Sampel
• Bagan atribut memerlukan ukuran sampel yang
lebih besar
• 50 sampai 100 bagian dalam sampel
• Grafik variabel memerlukan sampel yang lebih
kecil
• 2 sampai 10 bagian dalam sampel

53. Kemampuan Proses
• Membandingkan variabilitas natural terhadap variabilitas
desain
• Variabilitas natural
• Apa yang kita ukur dengan diagram kontrol
• Rata-rata proses = 8,80
• Deviasi standar = 0,12
• Toleransi
• Spesifikasi desain yang mencerminkan kebutuhan
produk
• Berat bersih = 9,0 gr  0,5 gr
• Toleransinya adalah  0,5 gr

54. Kemampuan Proses
(b) Spesifikasi desain dan
variasi natural yang sama;
Prosesnya mampu
memenuhi spesifikasi pada
sebagian besar waktu.
Spesifikasi
Desain
Proses
(a) Variasi natural
melebihi spesifikasi
desain; Prosesnya tidak
mampu memenuhi
spesifikasi selamanya.
Spesifikasi
Desain
Proses

55. Kemampuan Proses
(c) Spesifikasi desain lebih
besar dari variasi natural;
Prosesnya selalu bisa
sesuai dengan spesifikasi.
Spesifikasi
Desain
Proses
(d) Spesifikasi lebih besar
dari variasi alami, tapi
proses berada di luar titik
tengah; mampu tetapi
beberapa output tidak akan
memenuhi batas
spesifikasi atas.
Spesifikasi
Desain
Proses

56. Rasio Kemampuan Proses
Cp =
Jangkauan Toleransi
Jangkauan Proses
Toleransi Atas - Toleransi Bawah
6
=

57. Rasio Kemampuan Proses
Cp > 1, prosesnya mampu menghasilkan 99,7% bagian
dalam toleransi (dan dikatakan mampu)
Cp < 1, prosesnya dikatakan tidak mampu
Cp > 1,33 telah menjadi standar untuk menunjukan
kemampuan proses.
Cp menunjukkan apakah variasi proses cukup memuaskan,
tapi tidak mengukur apakah proses terpusat dengan benar
atau tidak.

58. Contoh Menghitung Cp
Spesifikasi berat bersih = 9,0 gr  0,5 gr
Proses rata-rata = 8,80 gr
Standar deviasi proses = 0,12 gr
Cp =
= = = 1,39
Toleransi Atas - Toleransi Bawah
6
9,5 - 8,5
6(0,12)

59. Indeks Kemampuan Proses
Cpk = minimum
x - toleransi bawah
3
=
toleransi atas - x
3
=
,
Cpk < 1 : distribusi proses tidak sesuai spesifikasi desain,
proses tidak dapat diterima
1 < Cpk < 1,33 : distribusi proses hampir tidak dalam spesifikasi,
proses marjinal
Cpk > 1,33 : distribusi proses sesuai spesifikasi,
proses dapat diterima

60. Contoh Menghitung Cpk
Spesifikasi berat bersih = 9,0 gr  0,5 gr
Proses rata-rata = 8,80 gr
Standar deviasi proses = 0,12 gr
Cpk = minimum
= minimum , = 0,83
x - toleransi bawah
3
=
toleransi atas - x
3
=
,
8,80 - 8,50
3(0,12)
9,50 - 8,80
3(0,12)

61. Tentukan apakah proses produksi dapat diterima atau tidak.
Latihan
No Hasil Ukur Ø Hasil Ukur P
1 12,50 150,15
2 12,35 149,95
3 12,35 148,90
4 12,55 150,10
5 12,55 150,05
6 12,60 149,95
7 12,35 149,95
8 12,45 150,10
9 12,60 150,15
10 12,35 150,15
Ø12,5±0,1
150 ± 0,15

62. Terima kasih