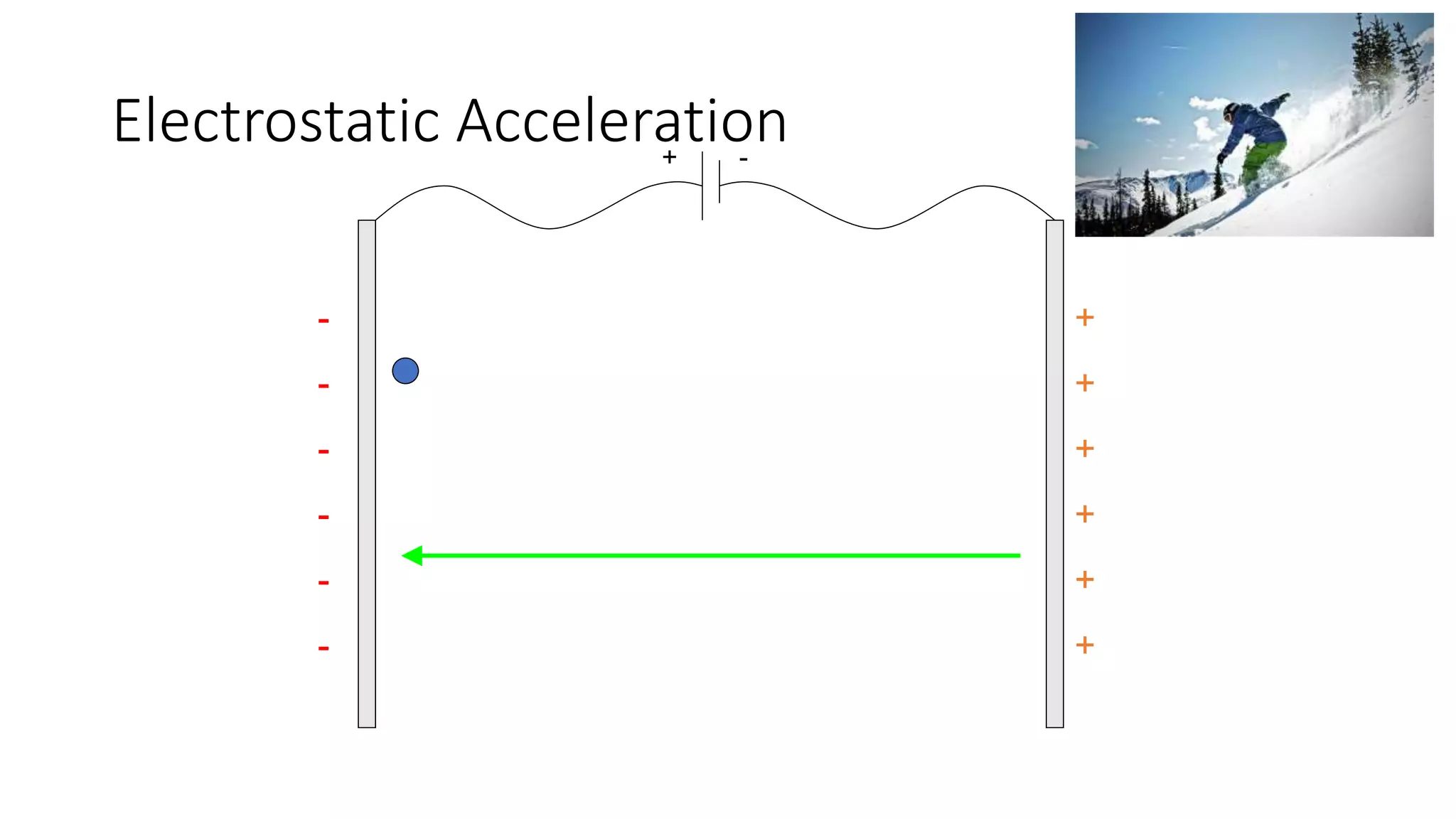
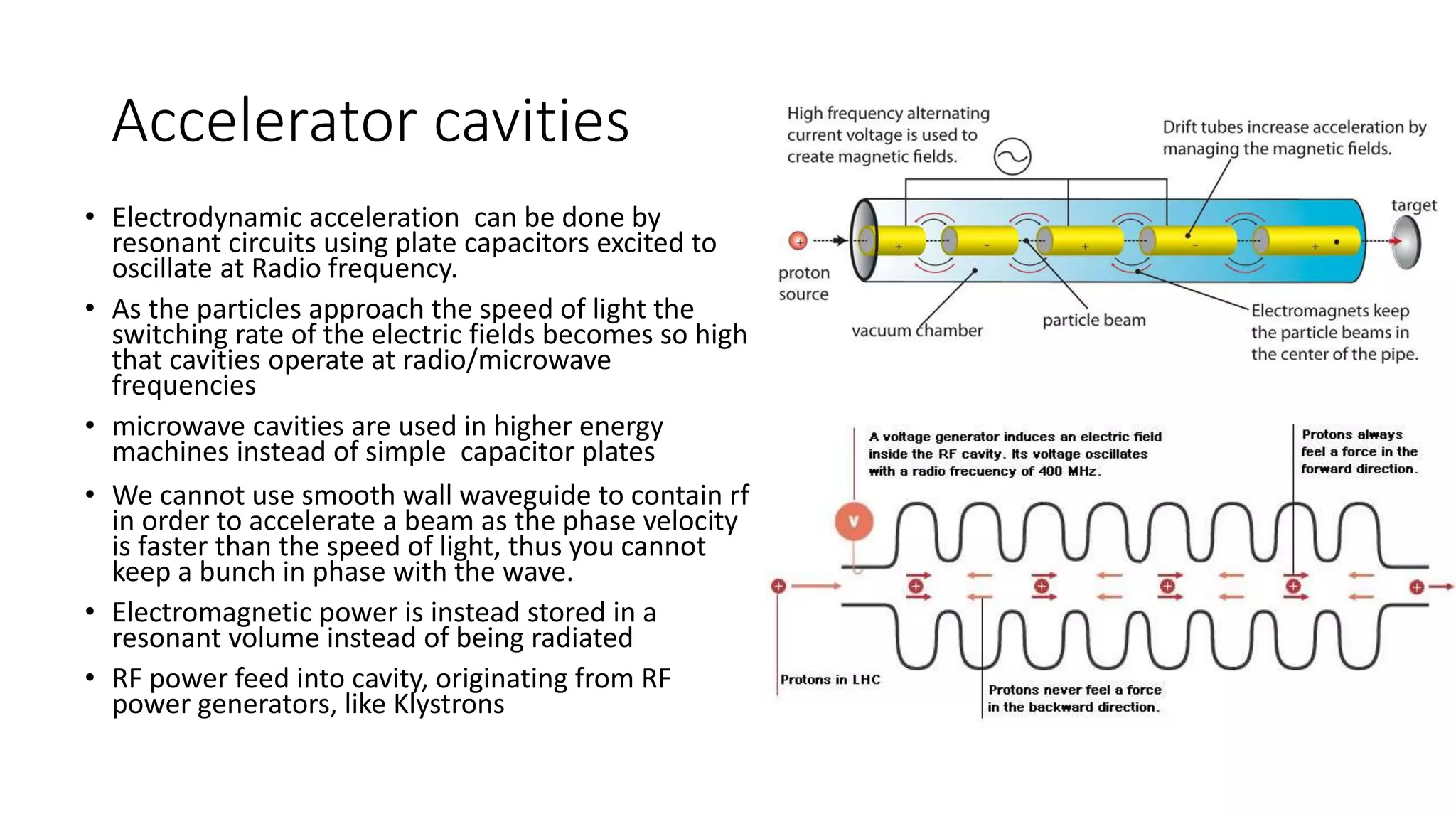
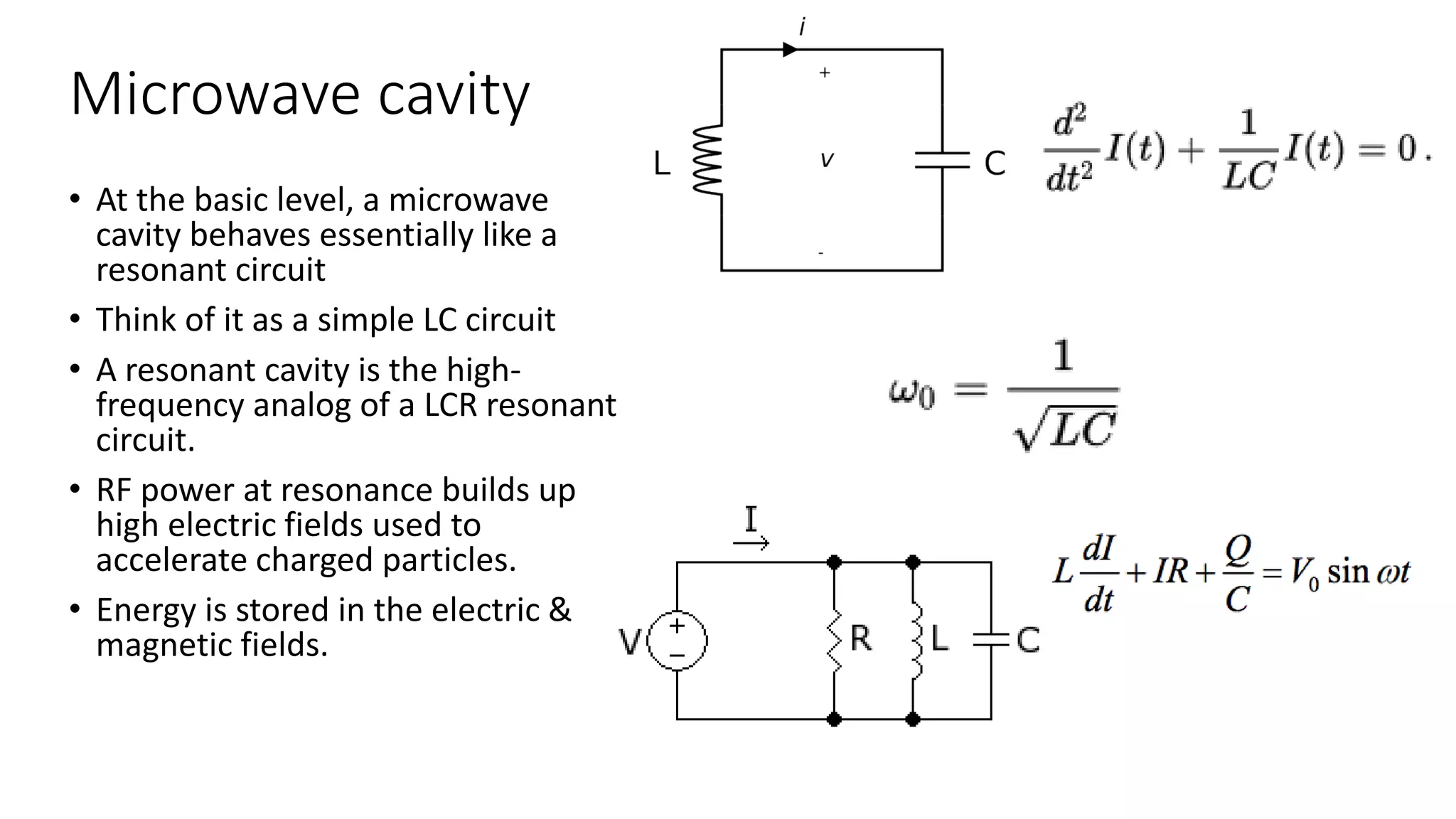
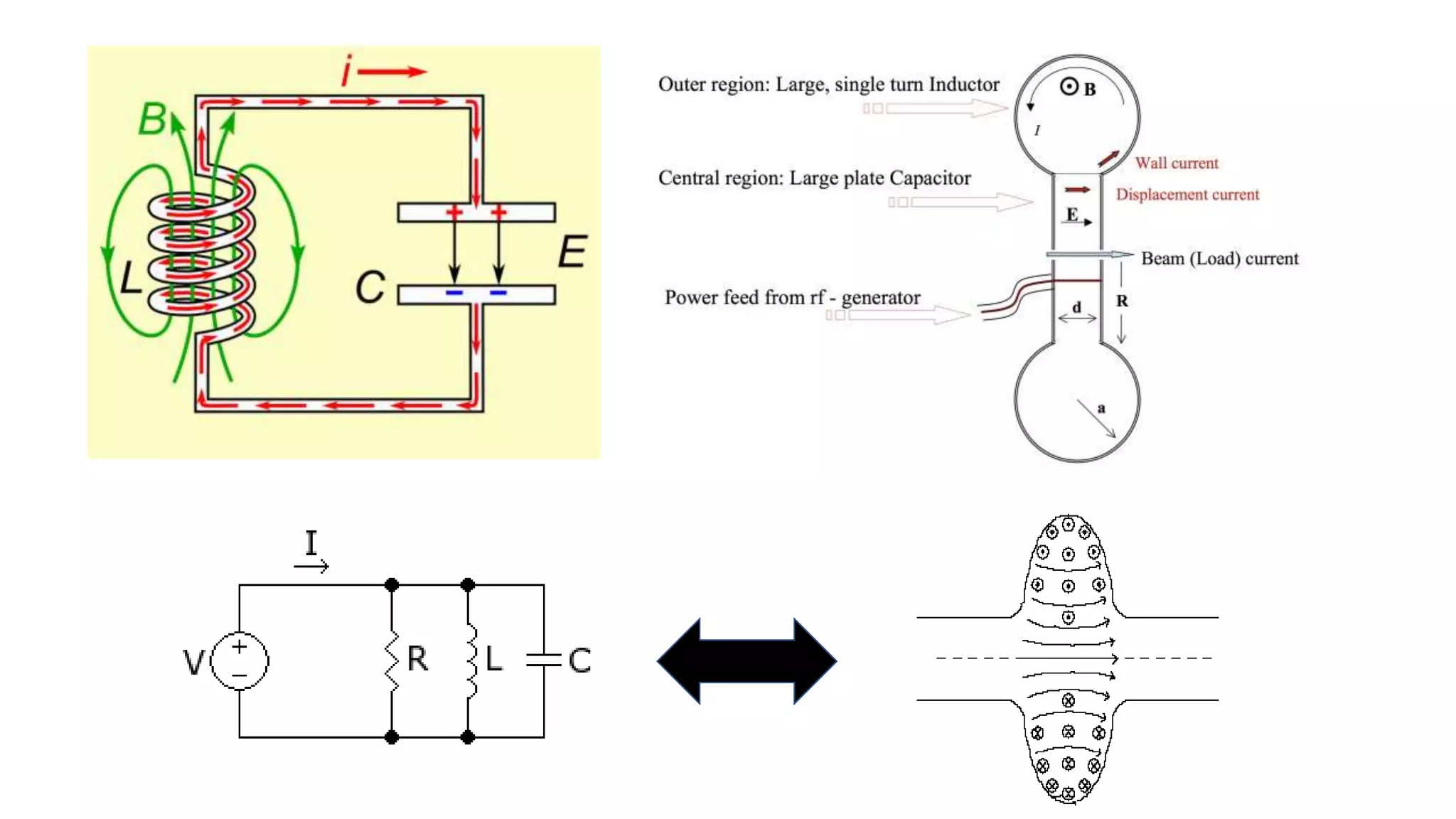
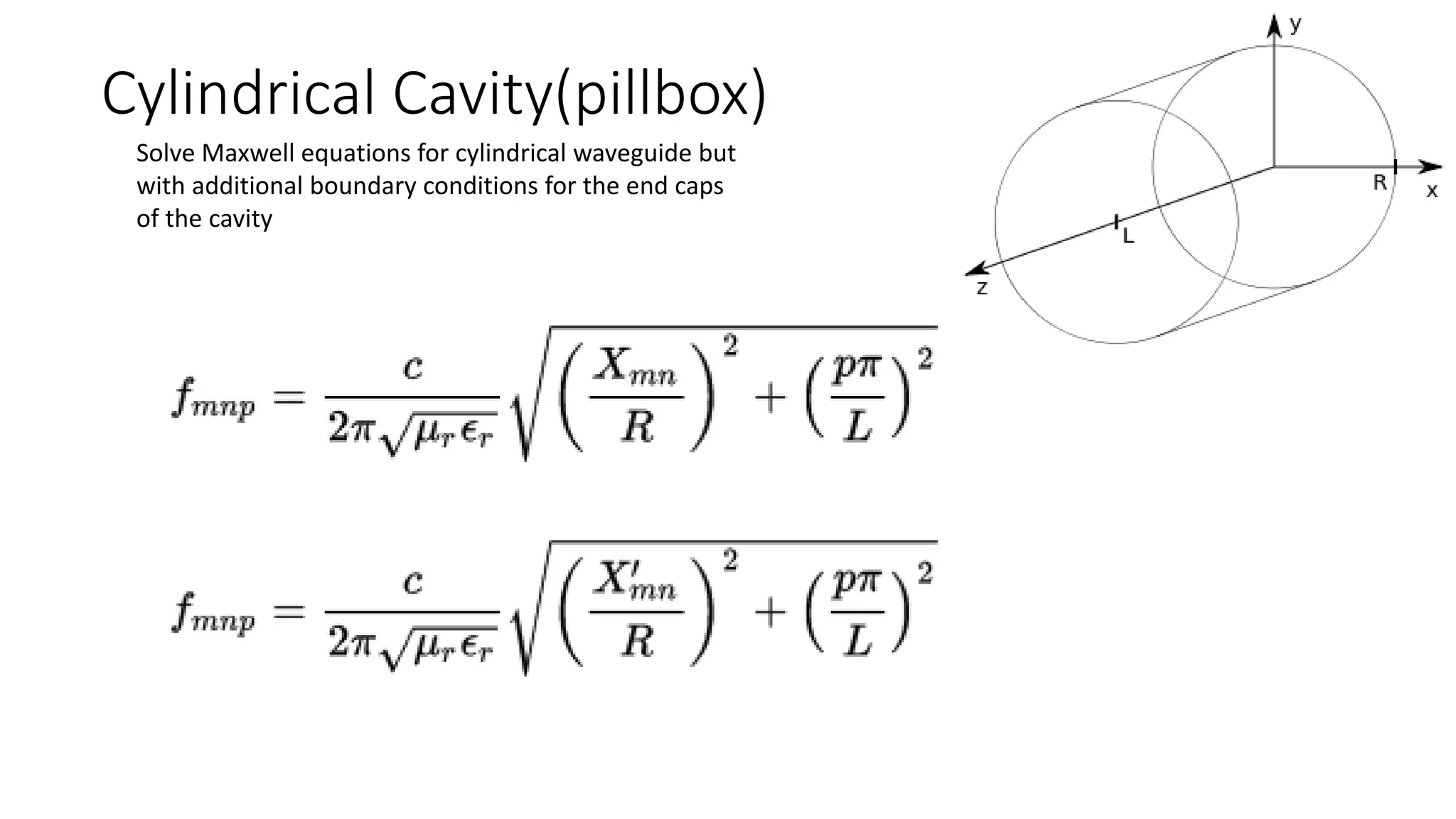
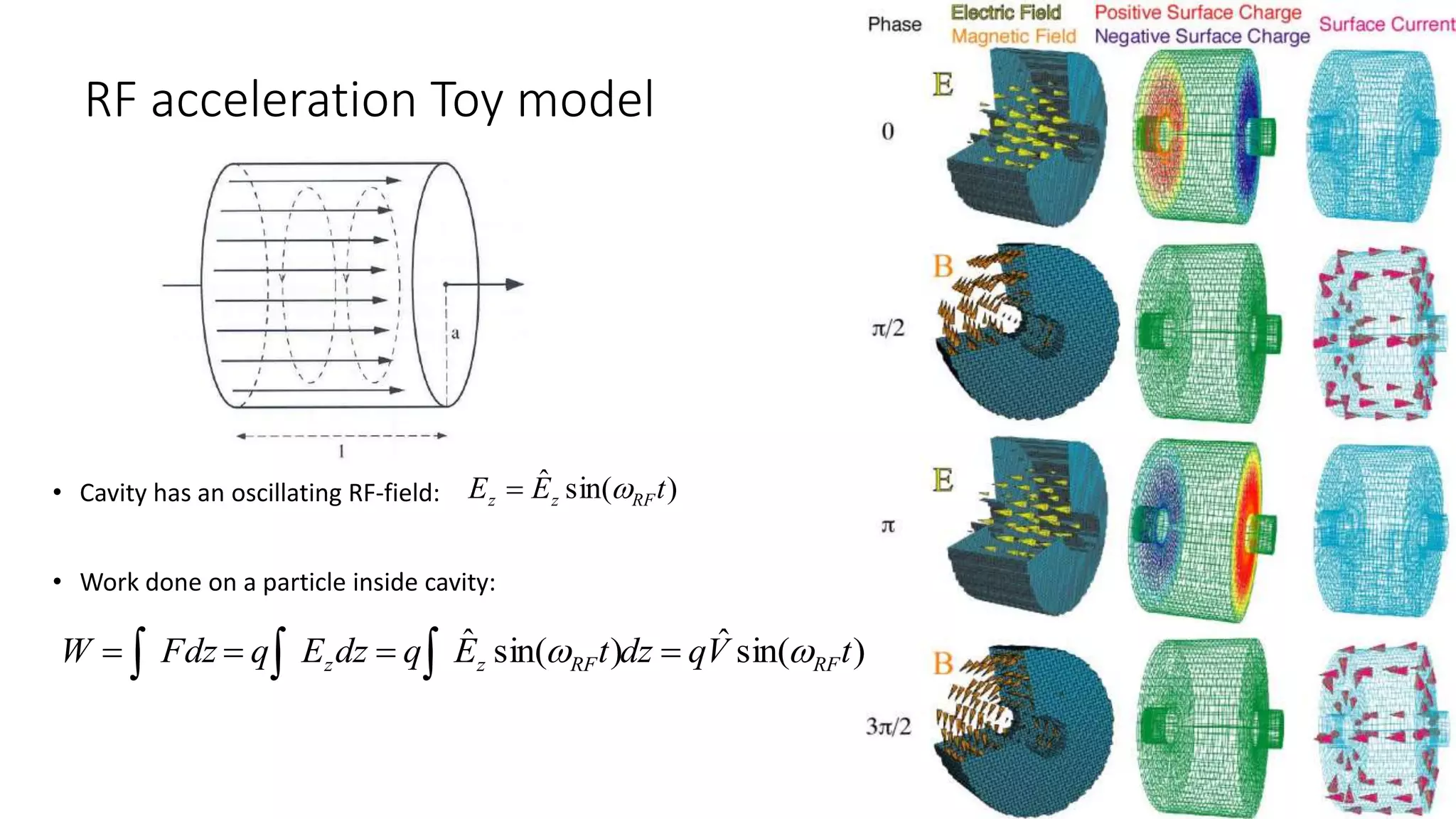
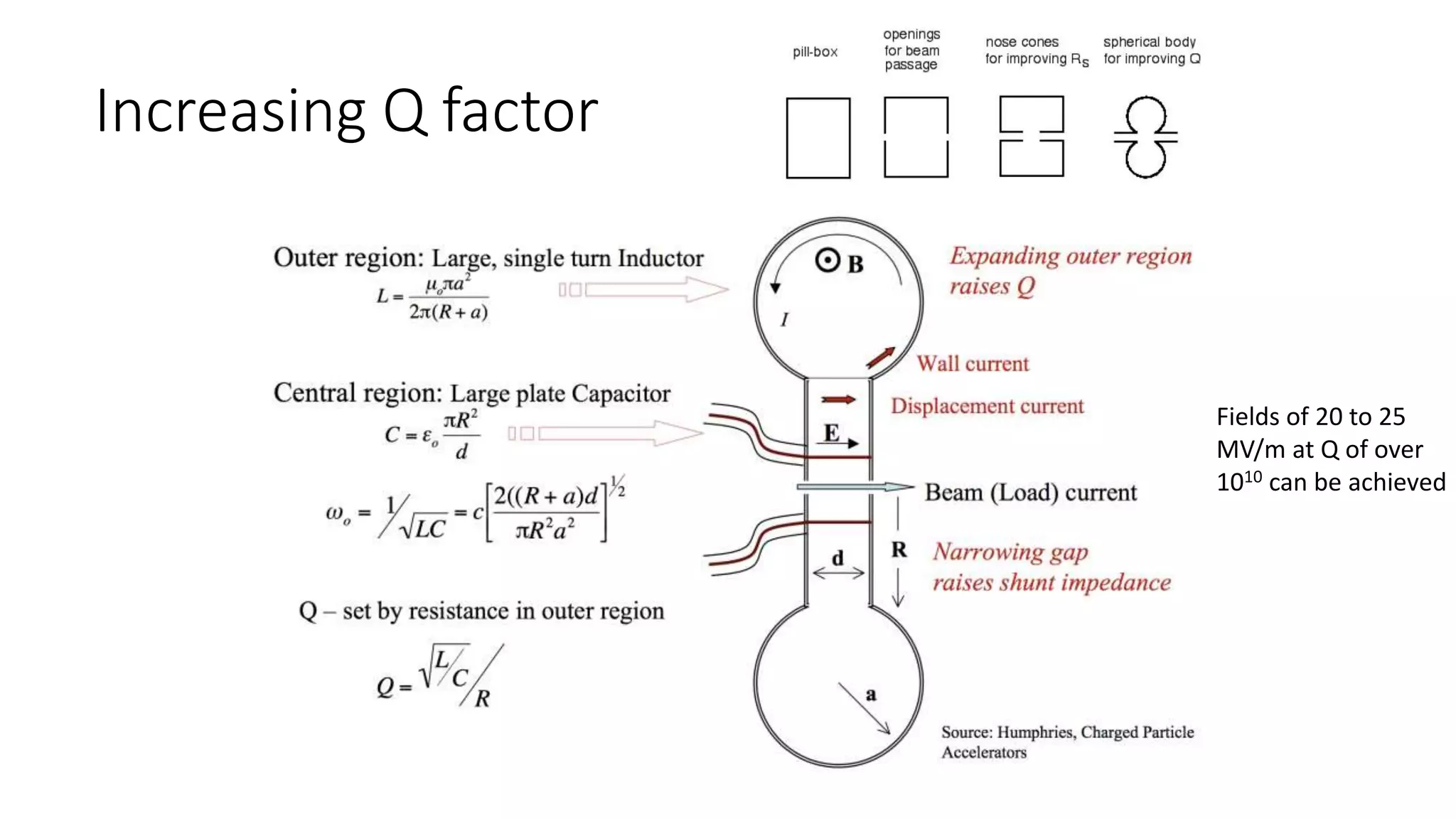
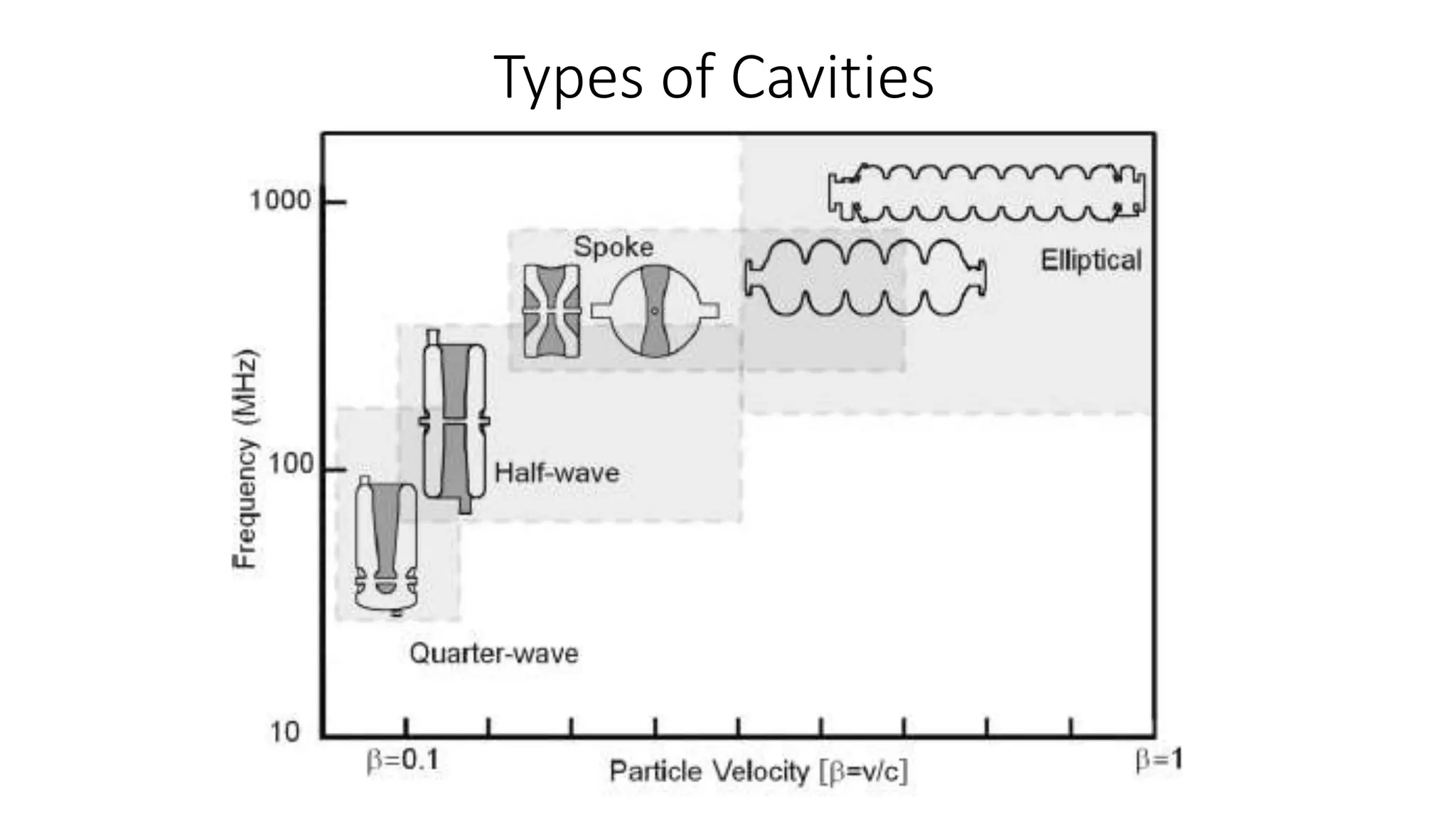
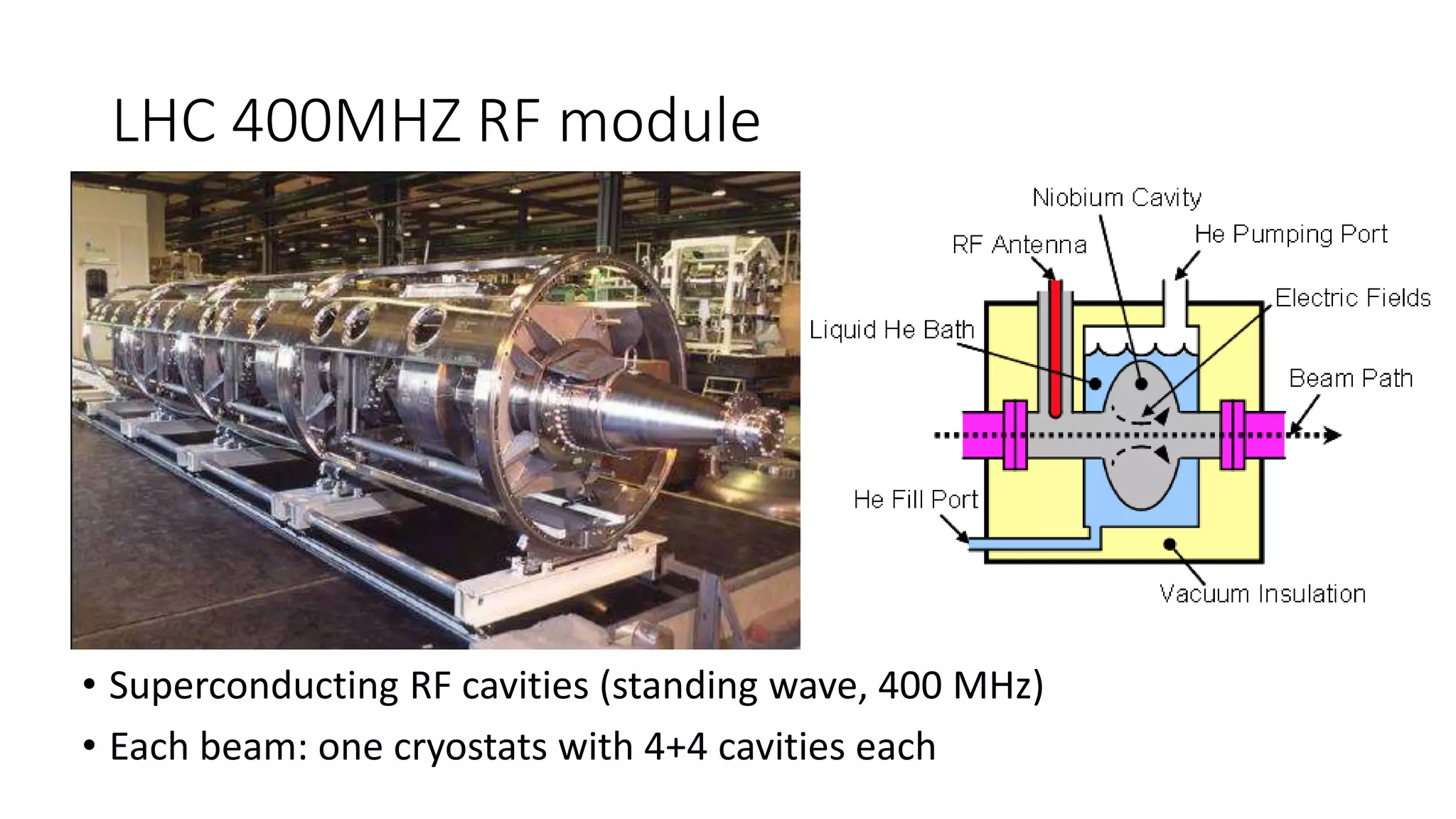
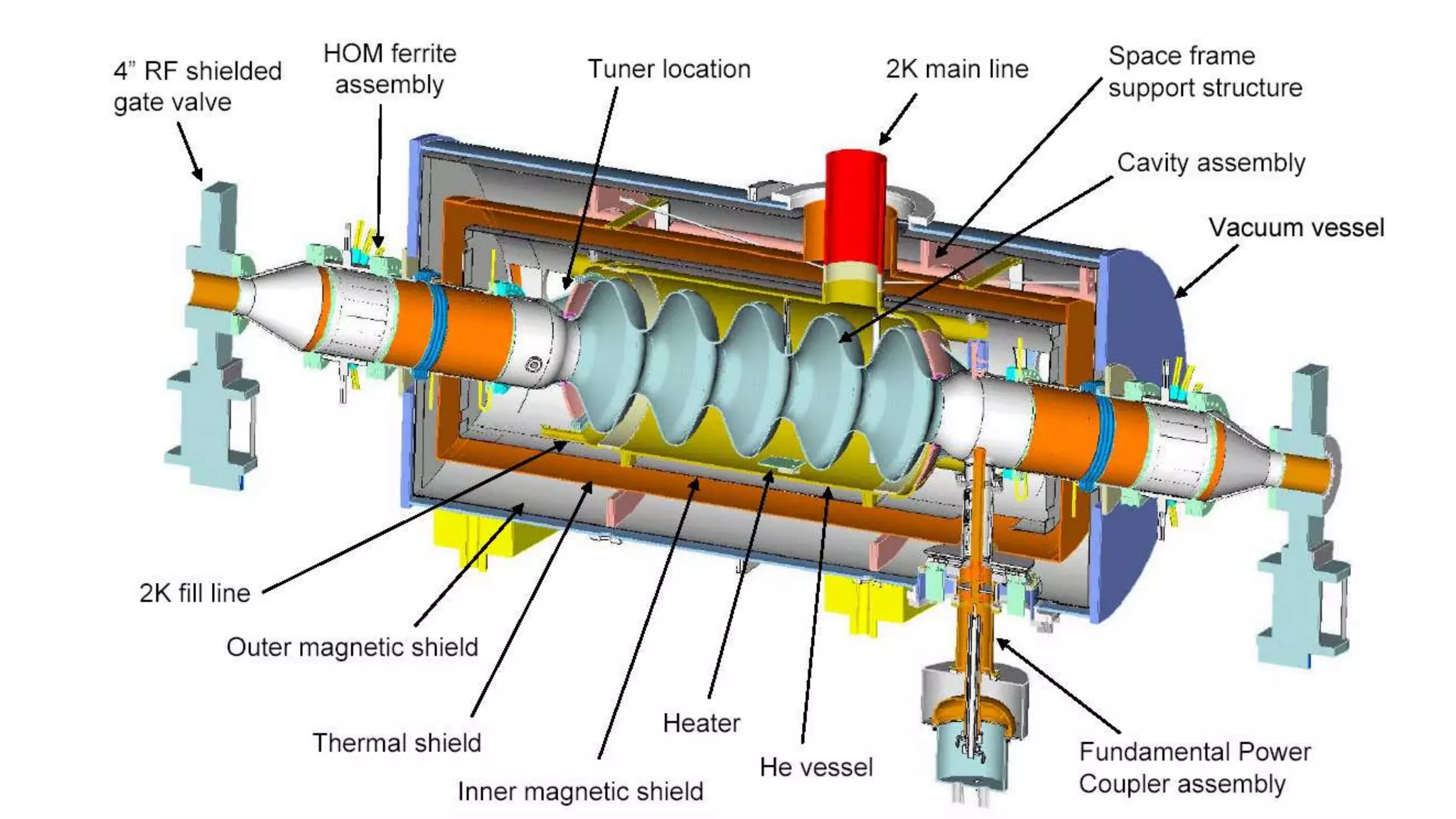
This document discusses particle accelerator cavities and electrodynamics. It explains that particle accelerators use electric fields to accelerate charged particle beams and magnetic fields to steer and focus them. Electrostatic accelerators directly use electric fields, while electrodynamic accelerators use oscillating electric fields to accelerate particles to higher energies. Radio frequency cavities operate as resonant circuits using oscillating electric fields from RF power sources to accelerate particle bunches in sync with the field oscillations. Superconducting RF cavities can achieve very high quality factors for particle acceleration. Common cavity types include quarter-wave and cylindrical pillbox designs.

1. Electrodynamics of particle
Accelerator Cavities
Erich Wanzek

2. Particle Accelerator basics
• Electromagnetism is the basis of the design of particle accelerators.
• Beams of Charged particles can be:
• Accelerated by electric field
• An steered and focused using magnetic fields
• Use Electric Field to do work on particle beam
• Use magnetic field to steer particle beam
• Electrostatic Accelerator use electrostatic fields to accelerate particles
• Achievable energies Limited by electrical breakdown of high E field Gradients at
millions of volts
• Electrodynamic Accelerators use changing (oscillating electric fields) to
accelerate particles
• Higher achievable energies, because beam passes through same field multiple times
instead of just once
BE FFBvqEqBvEqF

 )(

3. Electrostatic Acceleration
+
+
+
+
+
+
-
-
-
-
-
-
+ -

4. Electro dynamical Acceleration
- + - +
- + - +
By switching the charge on the plates in
phase with the particle motion, charged
particles will always see an acceleration
You only need to maintain a oscillating voltage between two plates not the
full static accelerating voltage of the accelerator.
The particles do need to “catch the waves” however, so particle bunches
must be bunched in phase with the oscillating fields.

5. Accelerator cavities
• Electrodynamic acceleration can be done by
resonant circuits using plate capacitors excited to
oscillate at Radio frequency.
• As the particles approach the speed of light the
switching rate of the electric fields becomes so high
that cavities operate at radio/microwave
frequencies
• microwave cavities are used in higher energy
machines instead of simple capacitor plates
• We cannot use smooth wall waveguide to contain rf
in order to accelerate a beam as the phase velocity
is faster than the speed of light, thus you cannot
keep a bunch in phase with the wave.
• Electromagnetic power is instead stored in a
resonant volume instead of being radiated
• RF power feed into cavity, originating from RF
power generators, like Klystrons

6. Electrodynamics of Micro wave cavities
• A microwave cavity is a resonator, consisting of a closed waveguide
metal structure that confines electromagnetic fields in the radio
microwave region of the spectrum.
• It is basically a waveguide that is deformed in a such a shape to
resonate standing electromagnetic waves with very high quality factor
• The electromagnetic waves reflect between the walls of the cavity. At
the resonate frequency of the cavity.
• The EM waves reinforce to form standing waves in the cavity

7. Microwave cavity
• At the basic level, a microwave
cavity behaves essentially like a
resonant circuit
• Think of it as a simple LC circuit
• A resonant cavity is the high-
frequency analog of a LCR resonant
circuit.
• RF power at resonance builds up
high electric fields used to
accelerate charged particles.
• Energy is stored in the electric &
magnetic fields.

9. Cylindrical Cavity(pillbox)
Solve Maxwell equations for cylindrical waveguide but
with additional boundary conditions for the end caps
of the cavity

10. RF acceleration Toy model
• Cavity has an oscillating RF-field:
• Work done on a particle inside cavity:
)sin(ˆ tEE RFzz 
)sin(ˆ)sin(ˆ tVqdztEqdzEqFdzW RFRFzz   

11. Transverse Magnetic Mode 010 TM010

12. Cavity Resonator Quality Factor

13. Increasing Q factor
Fields of 20 to 25
MV/m at Q of over
1010 can be achieved

14. Superconducting RF modules
• The ultra-low resistivity of a superconducting material allows an RF resonator to
obtain an extremely high quality factor
• A 1.3 GHz niobium SRF resonant cavity at 1.8 kelivn can obtain a quality factor
of Q=5×1010.
• Very high Q factor resonators store energy with very low loss and at a narrow
bandwidth.
• These properties are exploited for a variety of applications, including the
construction of high-performance particle accelerator structures.
• Had Galileo experimented with a 1 Hz resonator with a quality factor Q typical of
today's SRF cavities and left it swinging it would still be swinging today
• The motivation for using superconductors in RF cavities is not to achieve a net
power savings, but rather to increase the "quality" of the particle beam.

15. Types of Cavities

16. Quarter Wave

17. LHC 400MHZ RF module
• Superconducting RF cavities (standing wave, 400 MHz)
• Each beam: one cryostats with 4+4 cavities each

19. LHC parameters
Particle type p, Pb
Proton energy Ep at collision 7000 GeV
Peak luminosity (ATLAS,
CMS)
10 x 1034 cm-2s-1
Circumference C 26 658.9 m
Bending radius  2804.0 m
RF frequency fRF 400.8 MHz
# particles per bunch np 1.15 x 1011
# bunches nb 2808

20. Sources

21. Here is a video
• https://www.youtube.com/watch?v=MTEk39Yt55M