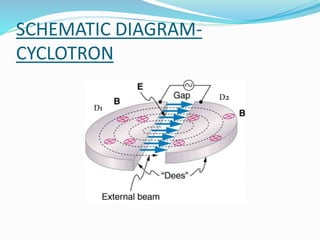
This document describes the working of a cyclotron particle accelerator. It explains that a cyclotron uses a magnetic field to curve the path of charged particles into a circular orbit, while an alternating electric field accelerates the particles at each half orbit. As the particles accelerate, they travel along spiraling paths of increasing radius. The document provides details on the construction of a cyclotron, including its dees and vacuum chamber between magnets. It also gives the mathematical expression for the cyclotron frequency that determines the electric field frequency needed for resonance acceleration. Limitations of the cyclotron are that particle mass may change at high speeds and it is difficult to accelerate low-mass particles like electrons.

1. Presented by,
Ruby Mathew
MTTC Pathanapuram

2. OUTLINE
 The purpose of an accelerator of charged
particles is to direct against a target a beam of a
specific kind of particles of a chosen energy.
 A particle accelerator is a device for
increasing the K.E. of electrically charged
particles.
There are many varieties of methods for
accomplishing this task, all using various
arrangements of electric and magnetic fields.

3. Cyclotron accelerators
It is used to accelerate particles to high energy.
 An electric field can accelerate a charged particle.
 A perpendicular magnetic field gives the ion circular path.
CONSTRUCTION
 Cyclotron consists of two semicircular dees D1 and
D2,enclosed in chamber. This chamber is placed in between
two magnets. An ac voltage is applied in between D1 and D2.
An ion kept in a vacuum chamber.
 At certain instant, let D1 be positive and D2 be negative,
Ion(+ve)will be accelerated towards D1 and describes a
semicircular path(inside it).When the particle reaches the
gap, D2,becomes negative and D1 become positive. So ion is
accelerated towards D2 and undergoes a circular motion with
larger radius . This process repeats again and again.
 Thus ion comes near the edge of the dee with high K.E This
ion can be directed towards the target by a deflecting plate.

4. SCHEMATIC DIAGRAM-
CYCLOTRON
D1
D2

5. MATHEMATICAL EXPRESSION
 The Lorentz force in the circular orbit, qv B , provides the centripetal
acceleration to maintain the circular motion at an instantaneous
radius ‘r ‘. Thus,
F = qv B = mv² ∕ r
v = q Br / m
the time taken for a semicircular orbit is,
time=distance/velocity
t = ∏r ∕ v = m∏ ∕ q B ; it shows that time is independent of radius and velocity.
The condition for resonance is half the period of the accelerating potential of
the oscillator should be ’ t’. (i.e., T∕2 = t). Hence the period of AC
T=2t
T=2∏m ∕q B [ since t = ∏m ∕q B ]
But we know frequency, ν = 1 ∕ T
therefore , Resonance frequency, ν = qB /2∏m
Which is often called “cyclotron frequency”
or “cyclotron resonance frequency.

6. K.E OF THE POSITIVE ION
KE = 1 ∕ 2 mv²
=1 ∕ 2 m(qBr∕m)²
i.e.,
KE = 1 ∕ 2( q²B²r²∕m)
Thus the kinetic energy that can be gained depends on
mass of particle ,charge of particle, magnetic field and
radius of cyclotron.

7. Limitations
(1 ) As the particle gains extremely high velocity, the mass of
particle will be changed from its constant value. This will
affect the normal working of cyclotron as frequency
depends of mass of particle.
(2) Another limitation of cyclotron is that very small
particles like electron can not be a accelerated using
cyclotron. This is because as the mass of electron is very
small the cyclotron frequency required becomes extremely
high which is practically difficult.

8. THANK YOU. . .