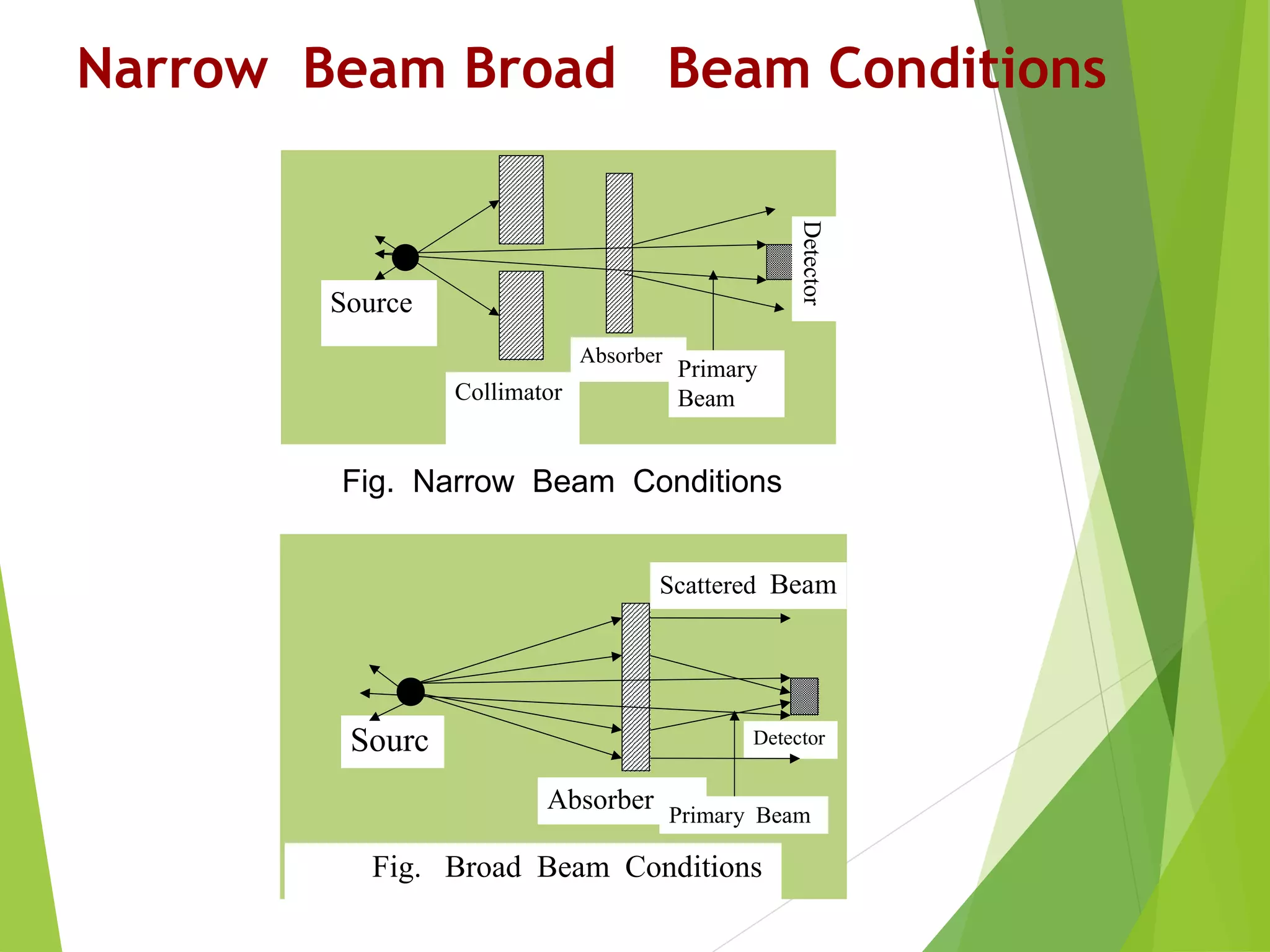
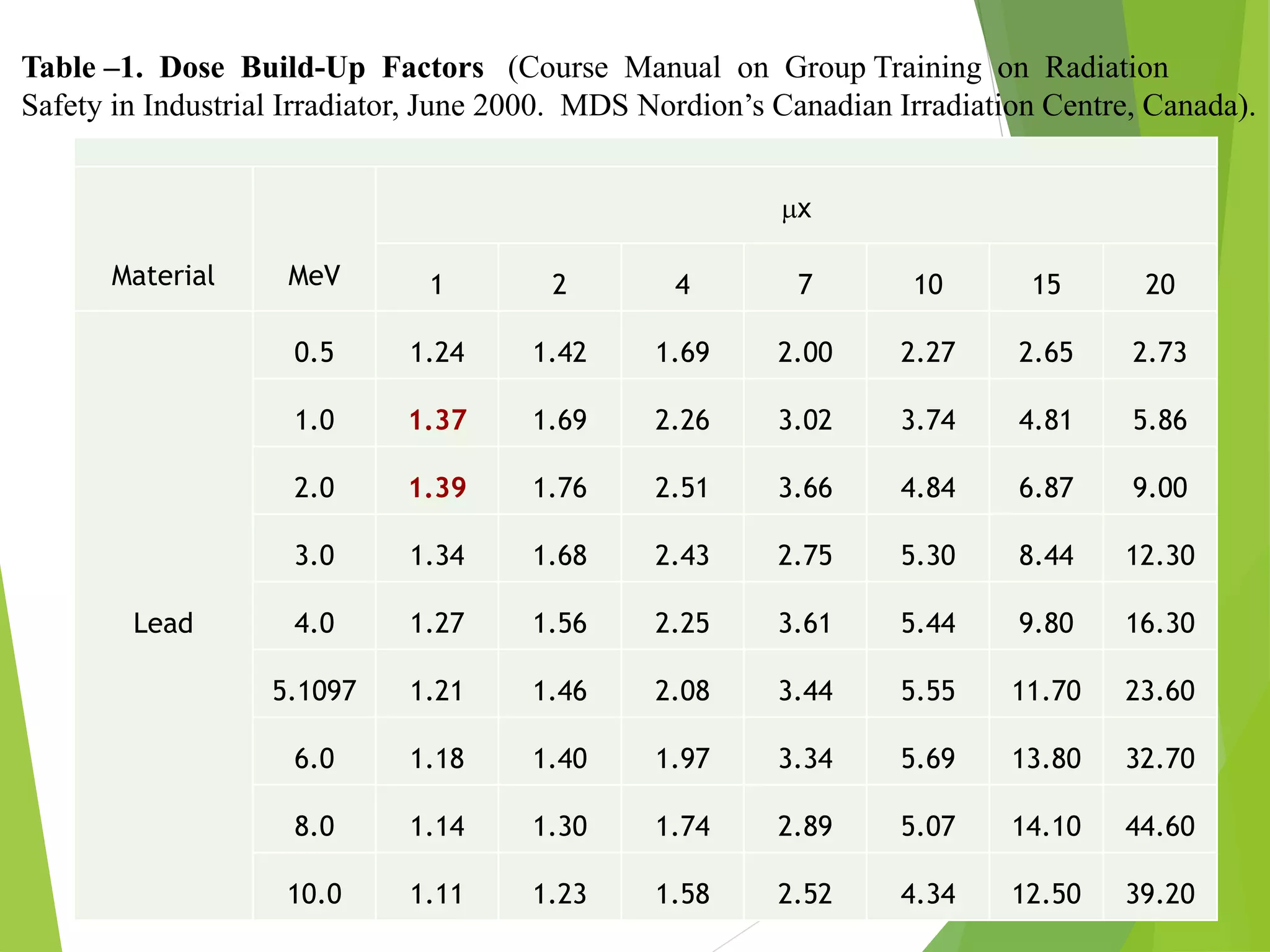
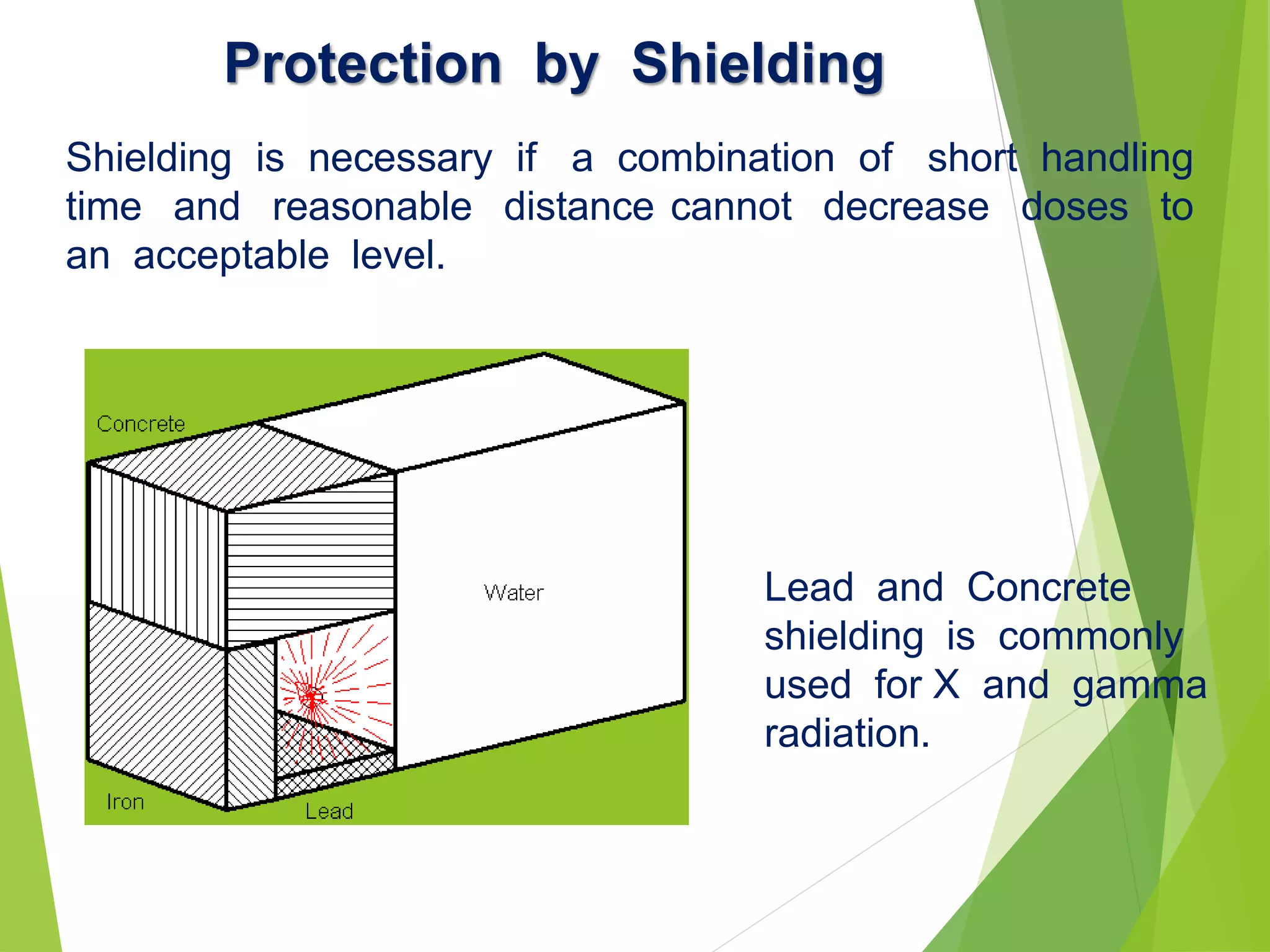
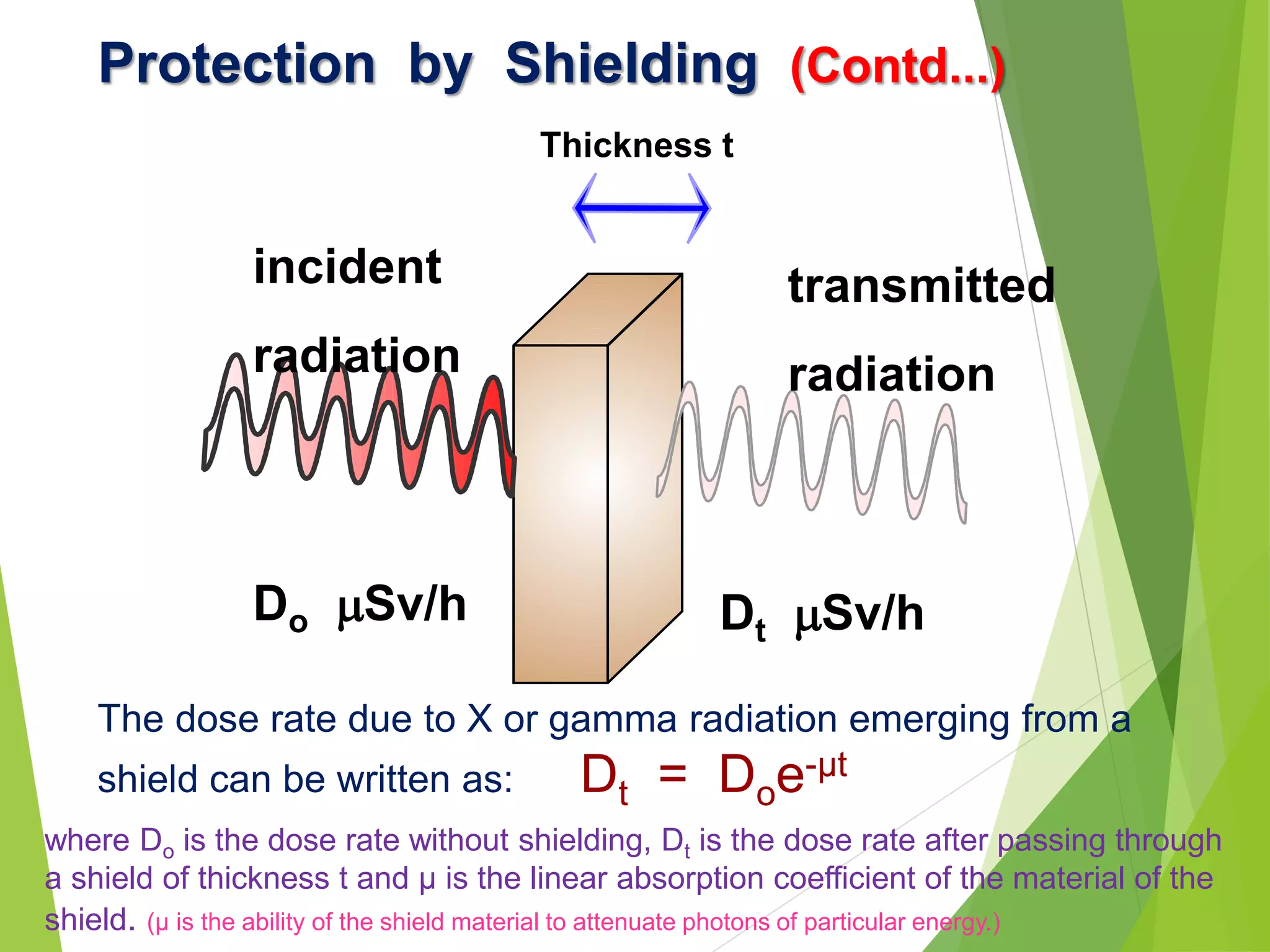
This document discusses radiation shielding concepts and calculation techniques necessary for protecting against radiation hazards, particularly for x and gamma radiation. It covers the importance of shielding materials, calculations for determining the thickness of shields required, and provides examples and problems related to radiation dose reduction through shielding. Additionally, it addresses half-life concepts and fast neutron shielding methods, emphasizing the need for materials rich in hydrogen for effective protection.

1. Institute of Nuclear Science and Technology
Atomic Energy Research Establishment, Savar, Dhaka
E-mail: dpaulbaec@yahoo.com
1
BASIC CONCEPT OF RADIATION SHIELDING
AND ITS CALCULATION TECHNIQUES
Dr. Debasish Paul
Chief Scientific Officer & Director
Training Course on Radiation Protection for Radiation Workers
and RCOs of BAEC, Medical Facilities & Industries
24 - 28 October 2021
Training Institute
Atomic Energy Research Establishment, Savar, Dhaka

2. INTRODUCTION
The preferred method of controlling the external
radiation hazard is by means of shielding.
The amount of shielding required depends on:
 the type of radiation
 the activity of the source and
 shielding material
 the dose rate which is acceptable outside the
shielding material.
2

3. Protection by Shielding
Shielding is necessary if a combination of short handling
time and reasonable distance cannot decrease doses to
an acceptable level.
Lead and Concrete
shielding is commonly
used for X and gamma
radiation.

4. Protection by Shielding (Contd...)
incident
radiation
transmitted
radiation
Thickness t
Do Sv/h Dt Sv/h
The dose rate due to X or gamma radiation emerging from a
shield can be written as: Dt = Doe-µt
where Do is the dose rate without shielding, Dt is the dose rate after passing through
a shield of thickness t and µ is the linear absorption coefficient of the material of the
shield. (µ is the ability of the shield material to attenuate photons of particular energy.)

5. Half-Value Layer (HVL)
incident
radiation
transmitted
radiation
HVL
Do Sv/h Dt = Do/2 Sv/h
A half-value layer (HVL) or half-value thickness (HVT), is
defined as the thickness of a material required to reduce the
intensity of a photon beam to half its initial value.
HVL or t1/2 = ln 2/µ = 0.693/

6. Determination of number of Half Value Layer
We know HVL or t1/2 = ln 2/µ = 0.693/
where,  is the linear absorption coefficient of the material.
Gamma and X-radiation, the dose rate can be written as;
Dt = Doe-t
where Do is the dose rate without shielding and Dt is the dose rate
after passing through a shield of thickness t.
This equation can be written as:
Nt = N0e-µt
where N0 is the original number of photons and Nt is number of
photons passing through a shield of thickness t.
Substituting the value of µ and using the properties of logarithms,
we can write: N0/Nt = 2t/t
1/2
Using this equation the number of HVL’S needed can be calculated.
6

7. Problem-1: It is necessary to reduce the source
of 5000 monoenergetic photons per second to
1000 photons per seconds. How many HVL’s of a
particular substance are needed?
Problem-2: Calculate the reduction in the
intensity of gamma-rays emitted by a Cs-137
source, if the source is placed in a lead container
2.7 cm thick, at some point outside the container.
7

8. Problem-3: The dose rate to a cobalt-60 source
is 160 Sv/h. How much lead shielding must be
placed around the source to reduce the dose rate
to 10 Sv/h? HVL of lead for 60Co gamma
radiation is 1.6 cm.
8

9. Half-life (T½)
Half-life (T1/2) is the time it takes for half of the atoms of a
radioactive material to decay.

10. Half-life (contd....)
Activity of the sample varies exponentially with time in accordance
with the equation:
A = A0 exp (-t) , where Ao is the initial activity, A is the activity at time
t and  is the decay constant.
For t = T1/2, A = A0/2 , this equation becomes
A0/2 = A0 exp (-T1/2) Or, ½ = exp (-T1/2) ,
Taking the natural logarithm ln (½) = -T1/2 or, - ln 2 = -T1/2 ,
Hence, T1/2 = ln 2 / = 0.693/
All radionuclides have a particular half-life, for example, uranium-238 has
such a long half-life of 4.47109 years and carbon-11 has a half-life of
only 20 minutes.

11. Some examples of half-lives
Fluorine-18 1.83 hours
Technetium-99m 6 hours
Thallium-201 3.04 days
Iodine-131 8 days
Phosphorus-32 14.3 days
Iridium-192 73.8 days
Cobalt-60 5.27 years
Caesium-137 30.2 years
Carbon-14 5730 years
Uranium-238 4.47 x 109 years

12. Problem-4: Calculate the activity of 30 mCi source of
11
24Na after 2.5 days. What is the decay constant of this
radionuclide? [ Half life = 15 hr]
12

13. Calculation of Shield Thickness
Gamma-ray absorption is an exponential process.
Following relationships can be used for calculation
shield thickness:
I = Ioe-x ………………… (1)
I = Iobe-x ….……………… (2) where
I is intensity of the radiation beam emerging from
the shielding material
Io is intensity of beam incident on shielding material.
 is linear absorption coefficient for shielding material.
x is the thickness of the shielding material, in cm.
b is the buildup factor if broad beam geometry is used

14. Narrow Beam Broad Beam Conditions
Source
Collimator
Absorber
Detector
Primary
Beam
Fig. Narrow Beam Conditions
Sourc
e
Absorber
Detector
Primary Beam
Fig. Broad Beam Conditions
Scattered Beam

15. Problem-5: A radiation field of 100 mR/h is
reduced by a lead shield of 2 cm thick. What is
the new dose rate? (Gamma energy is 1.5 MeV).
15

16. 16
Material MeV
x
1 2 4 7 10 15 20
Lead
0.5 1.24 1.42 1.69 2.00 2.27 2.65 2.73
1.0 1.37 1.69 2.26 3.02 3.74 4.81 5.86
2.0 1.39 1.76 2.51 3.66 4.84 6.87 9.00
3.0 1.34 1.68 2.43 2.75 5.30 8.44 12.30
4.0 1.27 1.56 2.25 3.61 5.44 9.80 16.30
5.1097 1.21 1.46 2.08 3.44 5.55 11.70 23.60
6.0 1.18 1.40 1.97 3.34 5.69 13.80 32.70
8.0 1.14 1.30 1.74 2.89 5.07 14.10 44.60
10.0 1.11 1.23 1.58 2.52 4.34 12.50 39.20
Table –1. Dose Build-Up Factors (Course Manual on Group Training on Radiation
Safety in Industrial Irradiator, June 2000. MDS Nordion’s Canadian Irradiation Centre, Canada).

17. Shielding For Fast Neutrons
 Fast neutron shielding materials should be rich in hydrogen.
Hydrogen will also capture low energy neutrons.
 Secondary gamma rays, with an energy 2.2 MeV are created as a
result of the capture of thermal neutrons by hydrogen.
 These capture gamma rays can be minimized by adding
Boron, Lithium or Cadmium.
5
10B + 0
1n 3
7Li + 2
4He + 0
0 (0.475 MeV)
Gamma photon released is of relatively low energy and easily shielded.
 Cadmium-113 also has high cross section for thermal neutron but
the reaction results in a 9.05 MeV gamma photon that creates an
additional shielding problem.
 Paraffin, wax, pure polyethylene are sometimes used as moderators
in neutron shielding to slow fast neutrons to thermal energies.
17

18. THANK YOU
18