Introduction To Survival Analysis

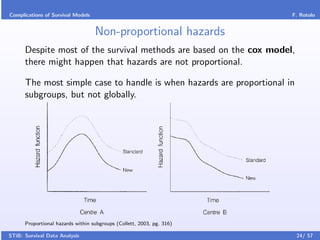
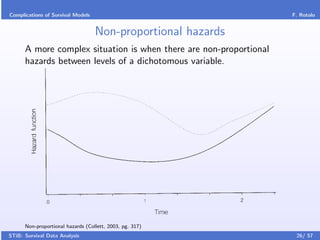
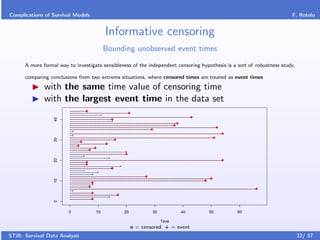
Special Topics in Biostatistics
An Introduction to Survival Data Analysis

Federico Rotolo
federico.rotolo@stat.unipd.it — federico.rotolo@uclouvain.be

Visiting PhD student at
PhD student at
Dipartmento di Scienze Statistiche Institut de Statistique, Biostatistique
et Sciences Actuarielles

Universit` degli Studi di Padova
a Universit´ Catholique de Louvain
e

March 30, 2011

F. Rotolo

Survival Analysis
Outline
An example

Peculiarities of Survival Data

Notation and Basic Functions

Survival Likelihood

Parametric models

Non-Parametric models

Regression
Complications of Survival Models

Non-proportional hazards

Informative censoring

Dependent observations

Multi-state phenomena

Competing Risks
References
STiB: Survival Data Analysis 2/ 57

Survival Analysis F. Rotolo

Survival Analysis

What is Survival Analysis?
The ﬁeld of statistics providing tools for handling duration data,
i.e. continuous and positive numerical variables measuring the
time from an origin event until the occurrence of an event of
interest.



Survival Analysis

interest.

Why “Survival” Analysis?
First works on this topic originated from the problem of studying
death times, that is times from birth to death.



Survival Analysis

interest.

Why “Survival” Analysis?
First works on this topic originated from the problem of studying
death times, that is times from birth to death.

Many ad-hoc statistical tools have been developed for survival
data (Cox model, Kaplan–Meier estimator, Mantel–Haenszel test, etc.) and
research interest in such problems has been increasing.
Why is Survival Data Analysis so peculiar?



An example

An example

Consider a clinical trial with patients undergone tumour surgical
removal.



An example

An example

Consider a clinical trial with patients undergone tumour surgical
removal.

One can be interested in
M: the level of a tumor marker after 6 months
T : the time until recurrence of the disease

In both cases the measured variable is continuous numerical and
positive, so there is no apparent diﬀerence.



An example

Actually, other situations can perturb the experiment before the
variable of interest is observed: the patient dies, gives up the
study, migrates, another disease occurs, the study ends, etc. . .



An example

Actually, other situations can perturb the experiment before the
variable of interest is observed: the patient dies, gives up the
study, migrates, another disease occurs, the study ends, etc. . .

In such cases
M is missing
T is missing and we know that T > s, with s the time of the
“disturbing event”



Censoring

Then the most particular feature of survival data is censoring.



Censoring


Right censoring (T > t) is very frequent and often unavoidable; all
survival methods account for it.
Interval censoring (T ∈ (l, r ]) is very frequent, too, but much more
ignored in usual practice.
Left censoring (T ≤ t) is very infrequent.



Censoring


Right censoring (T > t) is very frequent and often unavoidable; all
survival methods account for it.
Interval censoring (T ∈ (l, r ]) is very frequent, too, but much more
ignored in usual practice.
Left censoring (T ≤ t) is very infrequent.

Left truncation is a diﬀerent concept, concerning the selection
bias introduced by including in the study only subjects having a
survival time greater than a certain value, say t ∗ ; then we do not
observe T but T = T |T > t ∗ .



Conditioning

The second important feature of survival data is the concept of
conditioning, even more important than censoring according to
some authors (Hougaard, 2000).



Conditioning


As time passes, new information is available, not only for subjects
dying, but also for those surviving.



Conditioning


As time passes, new information is available, not only for subjects
dying, but also for those surviving.

In this case it is useful to consider, rather than the density f (t) of
T , its hazard function
f (t)
h(t) = ·
1 − F (t)



Survival Analysis
Consider the event time variable T with distribution F (t) and
density f (t) = dF (t)/dt.
The survival function is deﬁned as
S(t) = P(T > t) = 1 − F (t). (1)



Survival Analysis
Consider the event time variable T with distribution F (t) and
density f (t) = dF (t)/dt.
The survival function is deﬁned as
S(t) = P(T > t) = 1 − F (t). (1)

Then, the hazard function is
P(t ≤ T < t + ∆t|T ≥ t) f (t)
h(t) = lim = · (2)
∆t 0 ∆t S(t)

If the censoring time C is independent of the event time T , then h(t) coincides with
the Crude Hazard Function (Fleming & Harrington, 1991, Theorem 1.3.1)
P(t ≤ T < t + ∆t|T ≥ t, C ≥ t)
h# (t) = lim ·
∆t 0 ∆t



Survival Analysis

The cumulative hazard functions is deﬁned as
t
H(t) = h(u)du. (3)
0



Survival Analysis

The cumulative hazard functions is deﬁned as
t
H(t) = h(u)du. (3)
0

Since f (t) = −dS(t)/dt, then

S(t) = e −H(t) (4)

or, equivalently,
d
h(t) = − log{S(t)}.
dt



Hazard and Conditioning

The hazard function already contains conditioning. Then, it is
particularly advantageous in a survival context, as shown by
Hougaard (1999) in the following table.

In truncated
In full distribution
Quantity distribution given survival to time v
Survival function S(t) S(t)/S(v )
Density f (t) f (t)/S(v )
Hazard function h(t) h(t)

Conditioning corresponds to considering only actually possible
events, accounting for the past being ﬁxed and known.



Survival Likelihood

Since right censoring is almost unavoidable, the observable
variable is not the time T , but

Y = min(T , C )
(Y , δ), ,
δ = I(T ≤C )

with C ∼ G (·) the censoring time variable and IA the indicator variable on the set A.



Survival Likelihood


Y = min(T , C )
(Y , δ), ,
δ = I(T ≤C )


What we are interested in is inference on the survival distribution
and its parameters, the vector ζ.



Survival Likelihood


Y = min(T , C )
(Y , δ), ,
δ = I(T ≤C )


What we are interested in is inference on the survival distribution
and its parameters, the vector ζ.

What is the survival likelihood L(ζ; y )?



Survival Likelihood
The contribution of an event time yi to the likelihood is
T⊥
⊥C
L(ζ; yi ) = (1 − G (yi ))f (yi ) ∝ f (yi ) = h(yi )S(yi ).

The contribution of a right-censor time yi is
T⊥
⊥C
L(ζ; yi ) = g (yi )(1 − F (yi )) ∝ (1 − F (yi )) = S(yi ).

Under i.i.d. sampling of size n with T ⊥ C , the total likelihood is
⊥
n
L(ζ; y ) = {h(yi )}δi S(yi ). (5)
i=1



Parametric models

A parametric form can be assumed for the hazard function and its
parameters can be estimated via maximization of the likelihood (5).
The most common models are:

Exponential, with constant hazard h(t) = λ > 0
Weibull, with monotone hazard h(t) = λρt ρ−1 , (λ > 0, ρ > 0)

Gompertz, with monotone hazard h(t) = λ exp(γt)
(λ > 0, γ ∈ R) and a fraction (e λ/γ ) of long-term survivors if
γ<0
Piecewise Constant over m intervals with ﬁxed end points
{xq }, and hazard h(t) = m λq I(xq−1<t≤xq )
q=1



Parametric models

Comparison of parametric models (Hougaard, 2000, Table 2.6)

Property Exponential Weibull Gompertz Piecewise
constant
Increasing hazard possible No Yes Yes Yes
Continuous hazard Yes Yes Yes No
Estimate monotone (Constant) Yes Yes No
Non-zero initial hazard Yes No Yes Yes
Minimum stable Yes Yes No No
Explicit estimation Yes No No Yes
Needs choice of intervals No No No Yes
No. of parameters 1 2 2 m
Dim. of suﬀ.stat.
Complete data 1 n n 2m − 1
Censored data 2 2n 2n 2m
n = number of observations; m + 1 = number of intervals in the piecewise constant model




Non-parametric methods require no assumption on the form of
survival function.

In general, the most common NP estimator is the empirical
ˆ
distribution function F (t), but censoring prevents its use.




Non-parametric methods require no assumption on the form of
survival function.

In general, the most common NP estimator is the empirical
ˆ
distribution function F (t), but censoring prevents its use.

Two methods are very widely used:
ˆ
the Kaplan–Meier estimator SKM (t) of the Survival function
ˆ
the Nelson–Aalen estimator HNA (t) of the Cumulative
Hazard

ˆ ˆ
Note that SKM (t) = exp{−HNA (t)}.



Kaplan–Meier estimator
The Kaplan–Meier Product Limit estimator (Kaplan & Meier, 1958)
of the Survival Function is

ˆ Ni ,
SKM (t) = 1− (6)
Ri
i|ti ≤t

with {ti }i the observed event times, Ni the number of events at time ti and Ri the
number of survivors at time ti .



Kaplan–Meier estimator
The Kaplan–Meier Product Limit estimator (Kaplan & Meier, 1958)
of the Survival Function is

ˆ Ni ,
SKM (t) = 1− (6)
Ri
i|ti ≤t


Its variance can be evaluated by the Greenwood’s formula
(Greenwood, 1926; Meier, 1975):

ˆ ˆ Ni
V SKM (t) = [SKM (t)]2 ·
Ri (Ri − Ni )
i|ti ≤t



Nelson–Aalen estimator
Nelson (1969); Aalen (1976)

The Nelson–Aalen estimator

of the cumulative hazard function is

ˆ Ni ,
HNA (t) = (7)
Ri
i|ti ≤t




Nelson–Aalen estimator
Nelson (1969); Aalen (1976)

The Nelson–Aalen estimator

of the cumulative hazard function is

ˆ Ni ,
HNA (t) = (7)
Ri
i|ti ≤t


Its variance evaluated by the Greenwood’s formula is

ˆ Ni
V HNA (t) = ·
Ri2
i|ti ≤t



Cox proportional hazards model

The most common and popular model in survival analysis is by far
the Cox Regression Model (Cox, 1972).




The most common and popular model in survival analysis is by far
the Cox Regression Model (Cox, 1972).

For a subject with covariates vector x, the hazard is expressed as
Tβ
h(t; x) = h0 (t)e x , (8)

with β the linear regression parameters vector and h0 (t) the
so-called baseline hazard function, corresponding to the hazard of
a (hypothetical) reference subject with x = (0, . . . 0).



For any two subjects i and j with covariates xi and xj , the hazard
ratio
h(t; xi ) h0 (t) exp(xT β)
i
= = exp{(xi − xj )T β}
h(t; xj ) h0 (t) exp(xT β)
j

is time-constant, so the two hazard functions are proportional.



For any two subjects i and j with covariates xi and xj , the hazard
ratio
h(t; xi ) h0 (t) exp(xT β)
i
= = exp{(xi − xj )T β}
h(t; xj ) h0 (t) exp(xT β)
j

is time-constant, so the two hazard functions are proportional.

The hypothesis of Proportional Hazards (PH) is quite strong !

On the other hand, the regression parameters have a very
straightforward meaning. Indeed, if xi(k) = xj(k) + 1 and
xi(l) = xj(l) , ∀l = k, then
h(t; xi )
β(k) = log ·
h(t; xj )



Semiparametric approach

Under PH assumption, the likelihood (5) is
n
L(β, ξ; y ) = {h0 (yi ) exp(xT β)}δi exp {−H0 (yi ) exp(xT β)} , (9)
i i
i=1

with ξ are the baseline parameters and (β, ξ) corresponding to ζ.



Semiparametric approach

Under PH assumption, the likelihood (5) is
n
L(β, ξ; y ) = {h0 (yi ) exp(xT β)}δi exp {−H0 (yi ) exp(xT β)} , (9)
i i
i=1

with ξ are the baseline parameters and (β, ξ) corresponding to ζ.

If the interest is in the covariates effect, the baseline hazard can
be left unspecified and the likelihood can be profiled (Duchateau &
Janssen, 2008, pg.’s 24–26) reducing to the Partial Likelihood
n
exp (xT β)
i ,
L(β) = (10)
j∈R(yi ) exp(xT β)
j
i=1

where R(t) = {r |yr ≥ t} is the risk set at t.


Accelerated failure times model
Very less used is the Accelerated Failure Time Model (AFT),
where the covariates act directly on time via a scale factor.
In this case the probability of surviving is
S(t) = S0 (exp(xT β)t).



Consequently the density and the hazard functions are
f (t) = exp(xT β)f0 (exp(xT β)t)
h(t) = exp(xT β)h0 (exp(xT β)t).




The usual way of representing an AFT model is as loglinear
model of times
log T = xT α + .




The usual way of representing an AFT model is as loglinear
model of times
log T = xT α + .

In the (only) case of T ∼ Weibull, the model corresponds to a PH
regression.

Complications of Survival Models F. Rotolo

Outline
Survival Analysis






Competing Risks
Incidence

Covariates eﬀect

References



Most of the methods for Survival Data Analysis rest on some
hypotheses, notably
proportional hazards
uninformative censoring
independent observations
one type of unavoidable event




hypotheses, notably

How to test for these assumptions?

How to handle data not satisfying these assumptions?



Despite most of the survival methods are based on the cox model,
there might happen that hazards are not proportional.




The most simple case to handle is when hazards are proportional in
subgroups, but not globally.




The most simple case to handle is when hazards are proportional in
subgroups, but not globally.

Proportional hazards within subgroups (Collett, 2003, pg. 316)




The eﬀect of the treatment in the whole population is not
multiplicative, despite it is so within each centre.





What can be done is to use a stratiﬁed PH model

hij (t) = h0j (t) exp(xT β),
ij

where the hazard of patient i from center j is exp(xT β) times the
ij
baseline h0j (t) of the stratum (center) at each time point.





What can be done is to use a stratified PH model

hij (t) = h0j (t) exp(xT β),
ij

where the hazard of patient i from center j is exp(xT β) times the
ij
baseline h0j (t) of the stratum (center) at each time point.

Since different baselines are taken into account, the covariates
effect is multiplicative and it can be estimated thanks to usual
methods for PH cox models.



A more complex situation is when there are non-proportional
hazards between levels of a dichotomous variable.

Non-proportional hazards (Collett, 2003, pg. 317)


A more complex situation is when there are non-proportional
hazards between levels of a dichotomous variable.

Non-proportional hazards modelled as PH (Collett, 2003, pg. 317)


Hazards can be modelled as proportional in a series of k
consecutive time intervals, obtaining the piecewise PH model
  
 k 
hi (t) = h0 (t) exp xi β1 + βj zj (t) ,
 
j=2

where xi is 0 for standard treatment and 1 for new treatment and the
zj (t)’s are (time-varying) indicators for being in the j th interval.



  
 k 
hi (t) = h0 (t) exp xi β1 + βj zj (t) ,
 
j=2


Log-hazard ratio for treatments is now diﬀerent in each interval:
β1 for interval 1
β1 + βk for interval k > 1.




hi (t) = h0 (t) exp xi β1 + βj zj (t) ,


Log-hazard ratio for treatments is now different in each interval:

β1 for interval 1
β1 + βk for interval k > 1.

Testing PH assumption: if all βk ’s are not significantly different
from 0 then there is no evidence of non-PH.



hypotheses, notably






Most of the survival analysis methods are only valid under
independent censoring hypothesis:

Ci ⊥ Ti .
⊥




Most of the survival analysis methods are only valid under
independent censoring hypothesis:

Ci ⊥ Ti .
⊥

For censoring due to end of the study, independence is reasonable.
For censoring due to loss to follow-up or competing risk it is much
more questionable.




Two typical situations (Putter et al., 2007):

Healthy participants feel less need for medical services oﬀered
by the study, and therefore quit.
→ C is negatively correlated with T
→ Overestimation of event risk




Two typical situations (Putter et al., 2007):

Healthy participants feel less need for medical services oﬀered
by the study, and therefore quit.
→ C is negatively correlated with T
→ Overestimation of event risk

Persons with advanced disease progression have become too
ill for further follow-up or they return to their country to
spend the last period with their family.
→ C is positively correlated with T
→ Underestimation of event risk



Empirical evaluation

An empirical way to check the uninformative censoring assumption
is to plot observed survival times against each regressor,
distinguishing censored and event times.



Empirical evaluation

An empirical way to check the uninformative censoring assumption
is to plot observed survival times against each regressor,
distinguishing censored and event times.
(a) (b)

+ +

+ + + + + + + +
++ +
50

50
+
+ +
+ + +
Time

Time
+
30

30
+ + + +
+ q + + + q

+ + +q q q
q
++ +
q
q q q
10

q
10 q

+ ++ + ++ ++ + ++ + + + +
+ + +
q q
q q q q

q + q
q
q
q + q
q q
q q

40 50 60 70 80 40 50 60 70 80

Age at diagnosis Age at diagnosis
o = censored; + = event
Example of data not suggesting (a) and suggesting (b) informative censoring


Bounding unobserved event times

A more formal way to investigate sensibleness of the independent
censoring hypothesis is a sort of robustness study, comparing
conclusions from two extreme situations, where censored times
are treated as event times

with the same time value of censoring time
with the largest event time in the data set




A more formal way to investigate sensibleness of the independent censoring hypothesis is a sort of robustness study,

comparing conclusions from two extreme situations, where censored times are treated as event times

o
o
+
o
40

o
+
o
o
o
o
+
o
+
o
30

o
o
o
o
o
o
+
o
+
+
20

o
o
o
+
o
+
+
+
o
o
10

o
o
+
o
o
+
o
o
+
o
0

0 10 20 30 40 50 60

Time





+
o
+
o
+
+ +
o
40

o
+
++
o
o
+
o +
o
+
+ +
o

+ +
o
30

o
+
o
+
o
+
o
++
o
o
+
+ +
o
+
+
20

o
+
o
+
o
+
+ +
o
+
+
+
o
++
o
10

o
+
o
+
+
o
+
o
+
+
o
+
o
+
+
o
0

0 10 20 30 40 50 60

Time





o ++o
+
+ +
o
40

o
+
++
o
o
+
o
+
+
o

+
+
o

+ +
o
30

o
o
o
+
+
o
o
+
+
o +
+
+
+
o
+
+
20

o
o
o
+
+
+
+
o +
+
+
+
o
++o
10

o
o
+
+
o + +
o
+
o
o
+
+
+
o +
0

0 10 20 30 40 50 60

Time



A more formal way to investigate sensibleness of the independent
censoring hypothesis is a sort of robustness study, comparing
conclusions from two extreme situations, where censored times
are treated as event times

o ++o
+
+ +
o
40

o
+
++
o
o
+
o
+
+
o

+
+
o

+ +
o
30

o
o
o
+
+
o
o
+
+
o +
+
+
+
o
+
+
20

o
o
o
+
+
+
+
o +
+
+
+
o
++o
10

o
o
+
+
o + +
o
+
o
o
+
+
+
o +
0

0 10 20 30 40 50 60

Time

If essentially the same conclusions can be drawn from the
original and these two models, then the censoring times can be
safely treated as independent of the event times.


Logistic regression

The most formal way of testing independent censoring hypothesis
is to use a linear logistic model with censoring variable as
response.



Logistic regression

response.

If any covariate results signiﬁcant in predicting whether the
event time is observed or censored, then the independence
hypothesis is quite unlikely.



Logistic regression

response.

If any covariate results signiﬁcant in predicting whether the
event time is observed or censored, then the independence
hypothesis is quite unlikely.

What to do?



Solutions are quite limited and no satisfactory way to overcome
the problem exists.



the problem exists.

Censoring all data before the ﬁrst censored observation makes
the censoring really independent of event times, but it is little
useful if this occurs early.
o
o
+
o
40

o
+
o
o
o
o
+
o
+
o
30

o
o
o
q
o
o
o
+
o
+
+
20

o
o
o
+
o
+
+
+
o
o
10

o
o
+
o
o
+
o
o
+
o
0

0 10 20 30 40 50 60

Time


the problem exists.

Censoring all data before the ﬁrst censored observation makes
the censoring really independent of event times, but it is little
useful if this occurs early.
o o
o o
o +
o o
40

o o
o +
o o
o o
o o
o o
+
o o
+
o o
30

o o
o o
o o
q
o
o o
o o
o +
o o
o +
o +
20

o o
o o
o o
o +
o o
o +
o +
o +
o o
o o
10

o o
o o
o +
o o
o o
+
o o
o o
o +
o o
0

0 10 20 30 40 50 60

Time



hypotheses, notably





Cox models and most of the survival analysis models assume that,
conditionally on possible regressors, event times are i.i.d.




This is an unreasonable assumption in many situations:
multi-centre studies
repeated measures on the same subject
inclusion of relatives in the same study
measures on similar organs from the same organism
paired samples
...




This is an unreasonable assumption in many situations:
multi-centre studies
repeated measures on the same subject
inclusion of relatives in the same study
measures on similar organs from the same organism
paired samples
...

If the group eﬀect is of interest, the factor is inserted in the model
as usual. More often one is only interested in controlling its
eﬀect in a parsimonious way in term of parameters.



The most common way to account for clustering in hazard
regression models is in a mixed model form (McCullagh & Nelder, 1989)
through a random eﬀect.
2
log{hij (t)} = log{h0 (t)} + wj + xT β,
ij wj ∼ IID(0, σw ).




2

The random eﬀect wj is unobservable and common to all
elements of a cluster.




2

The random eﬀect wj is unobservable and common to all
elements of a cluster.

Its actual realizations are not that important; on the contrary its
distribution is of primary interest to eliminate the variability
introduced by it.




In survival analysis, the model is usually expressed in the form
2
hij (t) = h0 (t)zj exp{xT β},
ij zj ∼ IID(1, σz ). (11)

with zj = e wj > 0 and is called Frailty Model (Duchateau & Janssen, 2008;
Wienke, 2009).




2
ij zj ∼ IID(1, σz ). (11)

Wienke, 2009).

The random variable zj was named frailty (term) by Vaupel et al.
(1979) as long as subjects with larger values have an increased
hazard, then they are more likely to die sooner.




2
ij zj ∼ IID(1, σz ). (11)

Wienke, 2009).

The random variable zj was named frailty (term) by Vaupel et al.
(1979) as long as subjects with larger values have an increased
hazard, then they are more likely to die sooner.

Note that the frailty is time-constant, so the hazard is increased or
decreased at any time.




The main consequences of this approach are two:
Dependence between event times in the same cluster
Thanks to that Frailty Models can account for dependency!
Non-proportionality of hazards in general
Hazards are still proportional conditionally on frailty values




The main consequences of this approach are two:
Dependence between event times in the same cluster
Thanks to that Frailty Models can account for dependency!
Non-proportionality of hazards in general
Hazards are still proportional conditionally on frailty values

Clusters can also have dimension 1, in which case all methods are
unchanged but their meaning and interpretation are quite
diﬀerent. (Univariate frailty models for overdispersion: Wienke, 2009, Chp. 3)



Many distributions can be used to model the frailty term; the most
common (Duchateau & Janssen, 2008, Chp. 4) are
Gamma, mathematically the most convenient: analytical
integration, closed under truncation
Log-Normal, the most consistent with the GLMM theory:
the random effects wj are Normal
Inverse-Gaussian, analytical integration
Positive-Stable, analytical integration and very flexible:
extends Gamma, Inverse-Gaussian, Positive-Stable and
compound-Poisson
Power-Variance-Function, very flexible: extends Gamma,
Inverse-Gaussian, Positive-Stable and compound-Poisson.
Closed under truncation




When a parametric model for the baseline hazard is assumed,
then the likelihood (9) can be used.
As long as the frailties are not known, the marginal likelihood is
considered:




considered:
s ∞ nj

Lmarg = hij (tij )δij S(tij )f (zj )dzj (12)
j=1 0 i=1

with s the number of clusters, nj the number of subjects in cluster j, hij (·) deﬁned as
in (11) and f (·) the density of zj .




considered:
s ∞ nj

Lmarg = hij (tij )δij S(tij )f (zj )dzj (12)
j=1 0 i=1

with s the number of clusters, nj the number of subjects in cluster j, hij (·) deﬁned as
in (11) and f (·) the density of zj .

Maximisation of (12) usually requires numerical methods, except
for particular cases (Duchateau & Janssen, 2008, Sec. 2.2, 2.4).




Note: βk are coeﬃcients of the conditional PH hazard model

⇓

βk has to be interpreted as a log-hazard ratio conditionally on the
frailty value, i.e. as a log-hazard ratio between two subjects in the
same cluster.




hypotheses, notably





Survival analysis can be regarded as the study of the times of
transition from a state (Alive) to another (Dead).

h(t)
Alive Dead




h(t)
Alive Dead

Some other intermediate states in between can be of interest, for
example the relapse of a treated disease.



Some other intermediate states in between can be of interest, for
example the relapse of a treated disease.

Alive without
Disease hD(t)

hR(t) Dead

Alive with hRD(t)
relapse

Can hD (t) and hRD (t) be considered equivalent? Probably not. . .


The two hazards, hD (t) and hR (t), with origin state Alive
without Disease can be modelled straightforwardly.




Example. Overall Survival

q
1

q
2
3

q
4

q
5

q
6
7

0 2 4 6 8 10

Time
(•: relapse; ×: censoring; : death)




Example. Transition D: Alive without Disease → Dead

q cen
1

q cen
2

cen
3

q cen
4

q cen
5

q cen
6

Event
7

0 2 4 6 8 10

Time




Example. Transition R: Alive without Disease → Alive with relapse

q Event
1

q Event
2

cens
3

q Event
4

q Event
5

q Event
6

cens
7

0 2 4 6 8 10

Time



The hazard hRD (t) requires considering life histories as truncated
at the time of relapse, from which subjects begin being at risk.

Example. Transition RD: Alive with relapse → Dead

q Event
1

q cens
2

cens
3

q cens
4

q Event
5

q Event
6

cens
7

0 2 4 6 8 10

Time



Competing Risks

A particular and common case of informative censoring is that
due to the presence of competing risks (CRs) which have common
causes with the event of interest.



Competing Risks

A particular and common case of informative censoring is that
due to the presence of competing risks (CRs) which have common
causes with the event of interest.

Example. Consider patients after surgical excision of cancer.
Interest is in distant metastasis (DM):
can local recurrence (LR) be considered as non-informative
censoring? Probably not!
what would be the eﬀect of reducing LR hazard, e.g. by
radiotherapy? Probably it would increase DM incidence, even
if its hazard is unchanged!



Competing Risks

Depending on the endpoint of the study, two possible approaches
(Pintilie, 2006) are possible:

Considering diﬀerent hazards simultaneously, taking into
account the interactions between causes of failure
→ the aim is to model the incidence of each type of event,
given the competition of the other events
Considering each cause of failure independently of all the
others, as if they didn’t exist
→ the aim is to get an insight into the biological process by
modelling the pure eﬀect of covariates on each hazard



Competing Risks
Incidence
In order to account for CRs, Prentice et al. (1978) extended the
definition of hazard (2), defining the cause-specific (C–S) hazard

P(t ≤ T < t + ∆t, K = i|T ≥ t) fi (t) ,
hi (t) = lim = (13)
∆t 0 ∆t S(t)

for i ∈ {1, . . . I }, with I the number of CRs and K the event type indicator.



Competing Risks
Incidence
In order to account for CRs, Prentice et al. (1978) extended the
definition of hazard (2), defining the cause-specific (C–S) hazard

P(t ≤ T < t + ∆t, K = i|T ≥ t) fi (t) ,
hi (t) = lim = (13)
∆t 0 ∆t S(t)

for i ∈ {1, . . . I }, with I the number of CRs and K the event type indicator.

The corresponding unconditional probability functions is

fi (t) = hi (t)S(t)

and is called subdensity function.

Note: this is not a density since R+ fi (t)dt < 1.


Competing Risks
Incidence
The corresponding subdistribution function is
t
Fi (t) = hi (u)S(u)du = P(T ≤ t, K = i) (14)
0

also named cumulative incidence function (CIF).



Competing Risks
Incidence
The corresponding subdistribution function is
t
Fi (t) = hi (u)S(u)du = P(T ≤ t, K = i) (14)
0

also named cumulative incidence function (CIF).

Note that ∞
Fi (∞) = fi (u)du = P(K = i) < 1
0

and that
Fi (t) + Si (t) = P(K = i) < 1 ∀t ≥ 0,

t
with Si (t) = exp{− 0 hi (u)du} the C–S survival function (see (3)–(4)).



Competing Risks
Incidence

The expression (14) of the CIF
t
Fi (t) = hi (u)S(u)du
0

clearly shows that the incidence of failure from a given cause i
depends not only on its C-S hazard hi (t), but also (inversely) on
other causes’ hazards through
 
I
S(t) = exp − Hj (t) .
j=1



Competing Risks
Incidence

Example. The expression of the CIF for DM is
t u u
FDM (t) = hDM (u)e − 0 hLR (v )dv −
e 0 hDM (v )dv
du.
0

Theerefore if, for instance, the C-S hazard of LR is increased of
25%, then the incidence of DM will be reduced by a factor of
e −0.25HLR (v ) .



Competing Risks
Incidence
MLE for the C-S hazard at the observed time tj is
ˆ
hi (tj ) = dij /nj ,
with dij the number of events of type i at time tj and nj the number of subjects at
risk at time tj (Marubini & Valsecchi, 2004, pg. 338).

MLE for the total survival function S(t) are simply provided by
K–M estimator (6).

Thus, the MLE for the CIF (Kalbﬂeisch, 1980, pg. 168) results
ˆ ˆ dij
Fi (t) = SKM (t) ,
nj
j|tj ≤t

and its variance can be computed, as usual, via Greenwood’s
formula (Greenwood, 1926).


Competing Risks
Covariates effect
The effect of covariates x can be accounted for by a regression
model, usually a cox model of the C-S hazard

hi (t; x) = h0i (t) exp (xT βi ) , i ∈ {1, . . . I }.

Both the baseline hazard h0i (t) and the coefficients βi are specific
of each type of event.
The model is fitted considering CR events as censored
observations, then the βi coefficients must be interpreted as
“pure” effects, as if no other risk existed.

On the contrary, the covariate vector is the same: this is a
recommendable practice because a covariate which is significant for
an event is likely to influence also the others, even if it does not
result significant.

References F. Rotolo

References I

Aalen, O. (1976). Nonparametric inference in connection with
multiple decrement models. Scandinavian Journal of Statistics
3, 15–27.
Collett, D. (2003). Modelling survival data in medical research.
CRC press.
Cox, D. R. (1972). Regression models and life-tables. Journal of
the Royal Statistical Society. Series B (Methodological) 34,
187–220.
Duchateau, L. & Janssen, P. (2008). The frailty model.
Springer.
Fleming, T. R. & Harrington, D. P. (1991). Counting
processes and survival analysis, vol. 8. Wiley New York.



References II
Greenwood, M. (1926). The natural duration of cancer.
Reports on public health and medical subjects 33, 1–26.
Hougaard, P. (1999). Fundamentals of survival data.
Biometrics 55, 13–22.
Hougaard, P. (2000). Analysis of multivariate survival data.
Springer Verlag.
Kalbfleisch, J. D. (1980). The statistical analysis of failure
time data, vol. 5. IEEE.
Kaplan, E. L. & Meier, P. (1958). Nonparametric estimation
from incomplete observations. Journal of the American
statistical association 53, 457–481.
Marubini, E. & Valsecchi, M. G. (2004). Analysing survival
data from clinical trials and observational studies.
Wiley-Interscience.



References III
McCullagh, P. & Nelder, J. A. (1989). Generalized linear
models. Chapman & Hall/CRC.
Meier, P. (1975). Estimation of a distribution function from
incomplete observations. Perspectives in Probability and
Statistics , 67–87.
Nelson, W. (1969). Hazard plotting for incomplete failure data.
Journal of Quality Technology 1, 27–52.
Pintilie, M. (2006). Competing risks: a practical perspective.
Wiley.
Prentice, R. L., Kalbfleisch, J. D., Peterson, A. V.,
Flournoy, N., Farewell, V. T. & Breslow, N. E.
(1978). The analysis of failure times in the presence of
competing risks. Biometrics 34, 541–554.



References IV

Putter, H., Fiocco, M. & Geskus, R. B. (2007). Tutorial in
biostatistics: competing risks and multi-state models. Stat Med
26, 2389–430.
Vaupel, J. W., Manton, K. G. & Stallard, E. (1979).
The impact of heterogeneity in individual frailty on the dynamics
of mortality. Demography 16, 439–454.
Wienke, A. (2009). Frailty Models in Survival Analysis.
Chapman & Hall/CRC biostatistics series. Taylor and Francis.


Introduction To Survival Analysis

More Related Content

What's hot

Similar to Introduction To Survival Analysis

Recently uploaded

Introduction To Survival Analysis