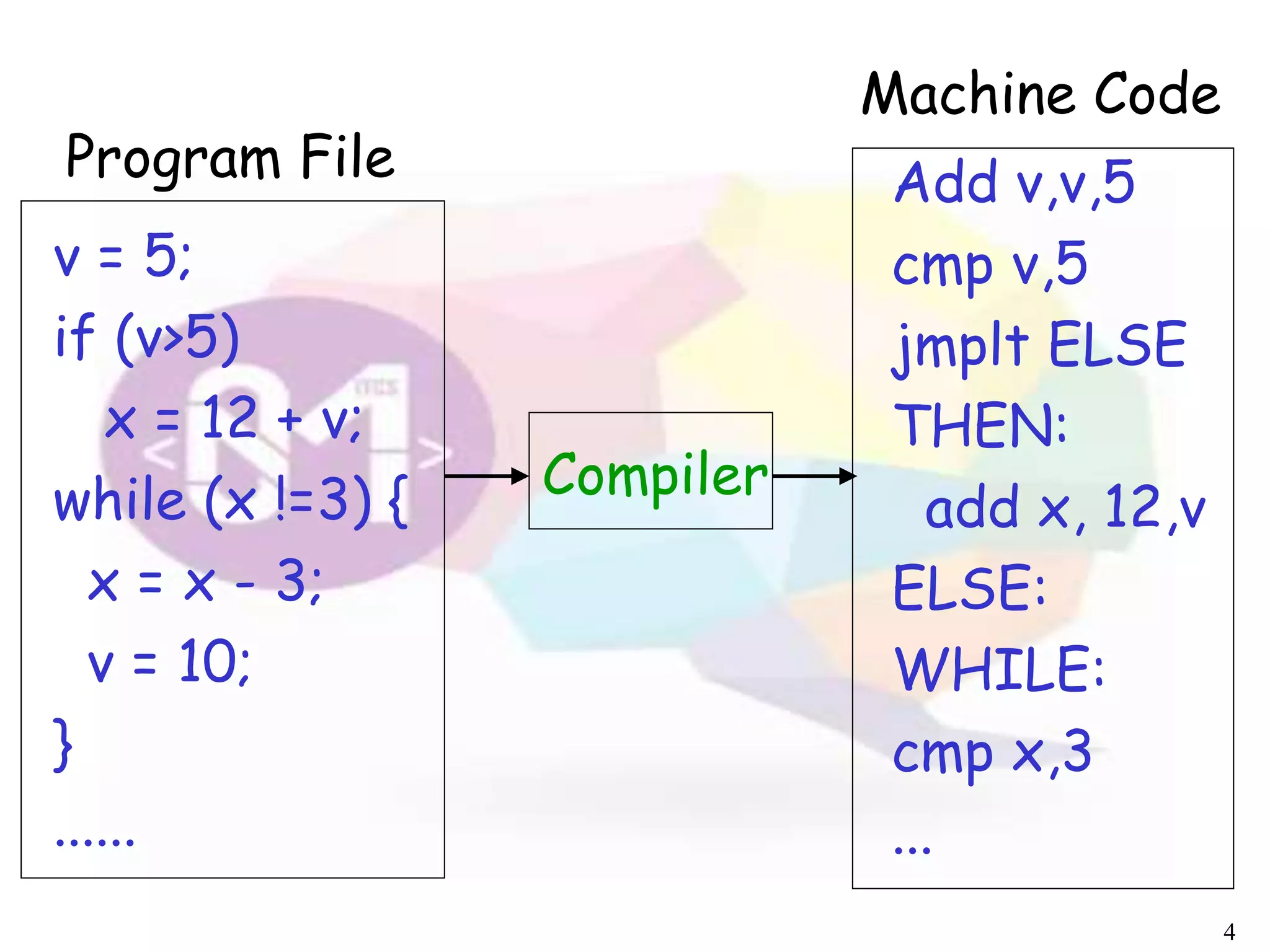
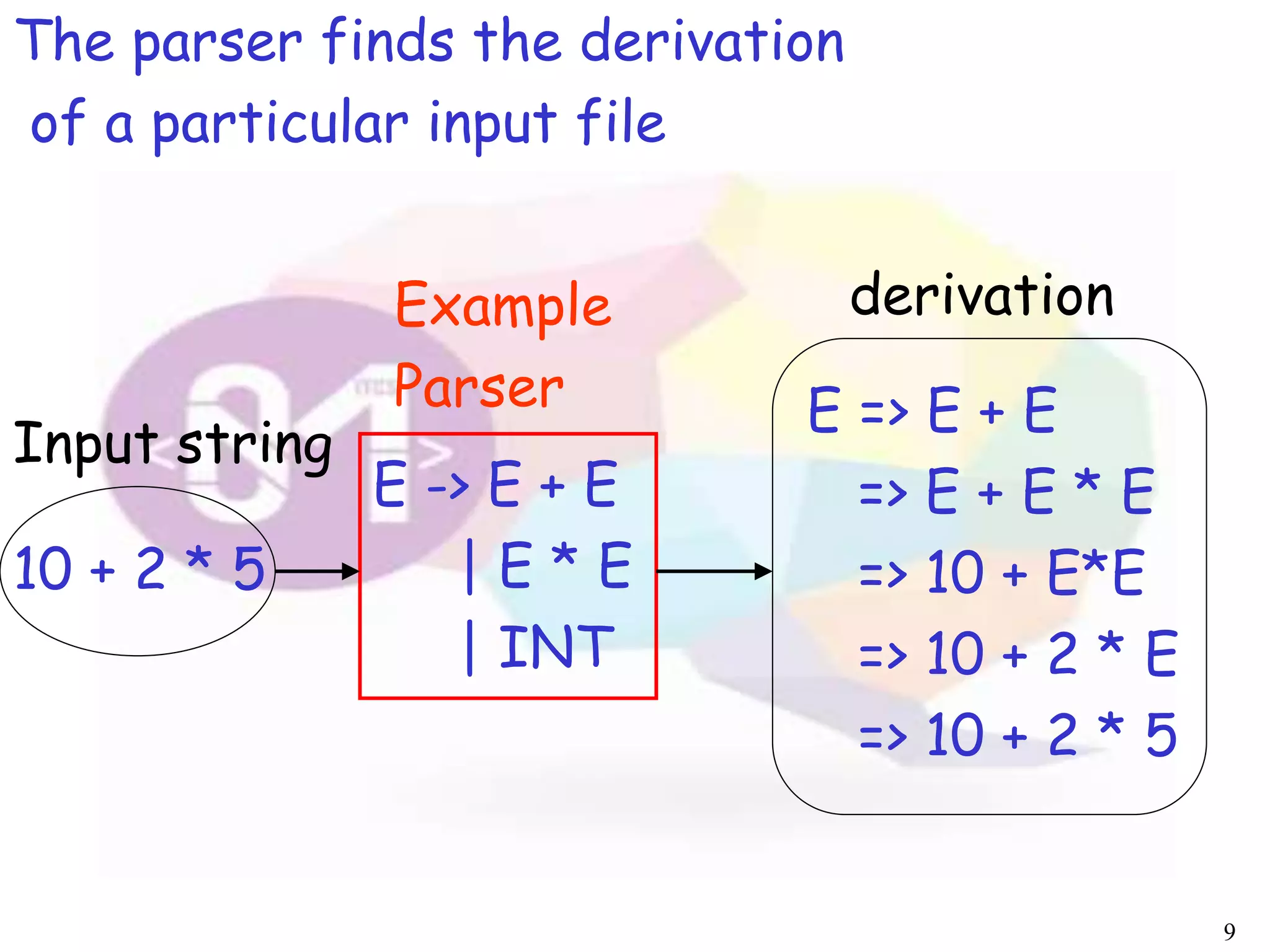
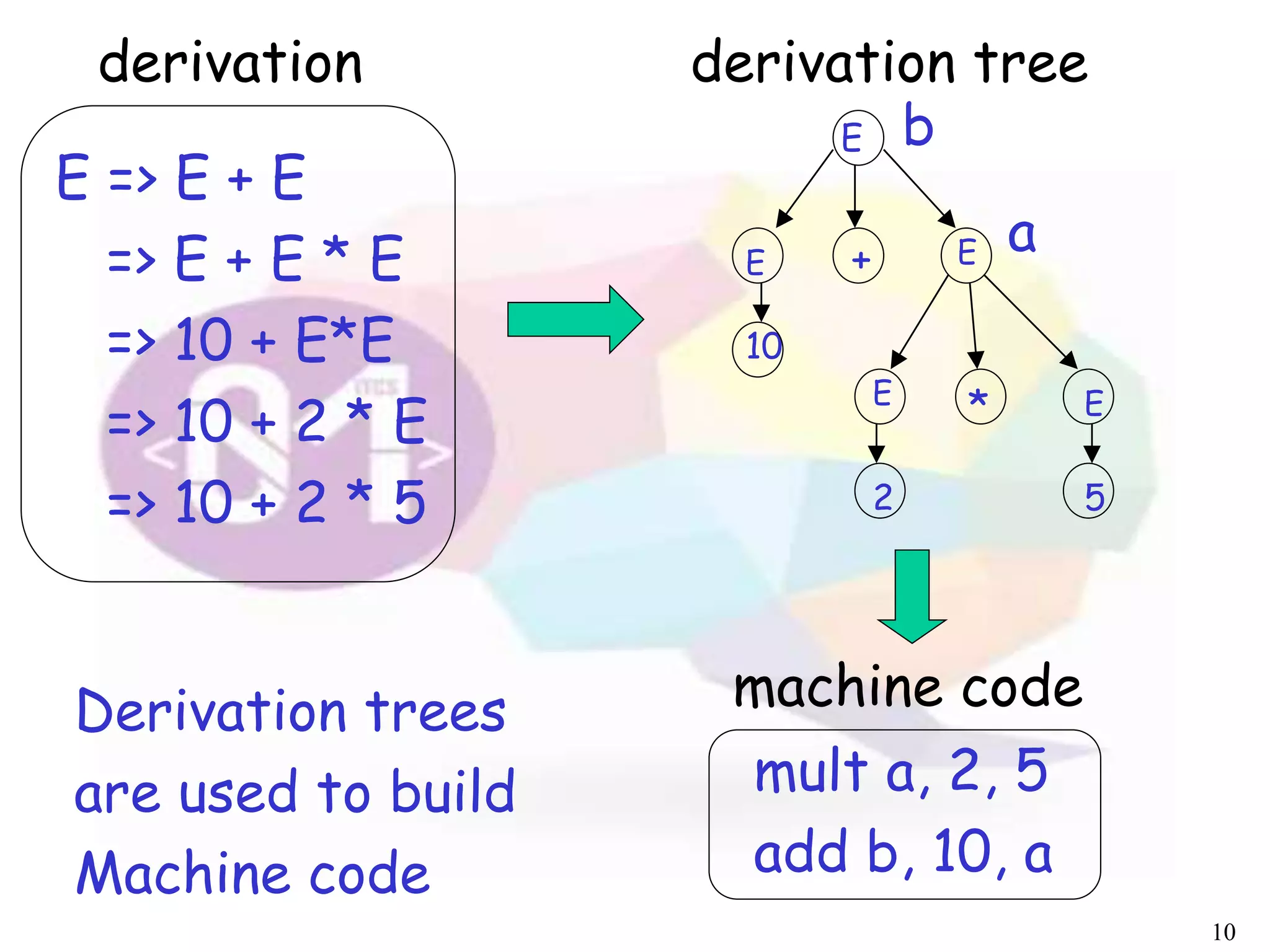
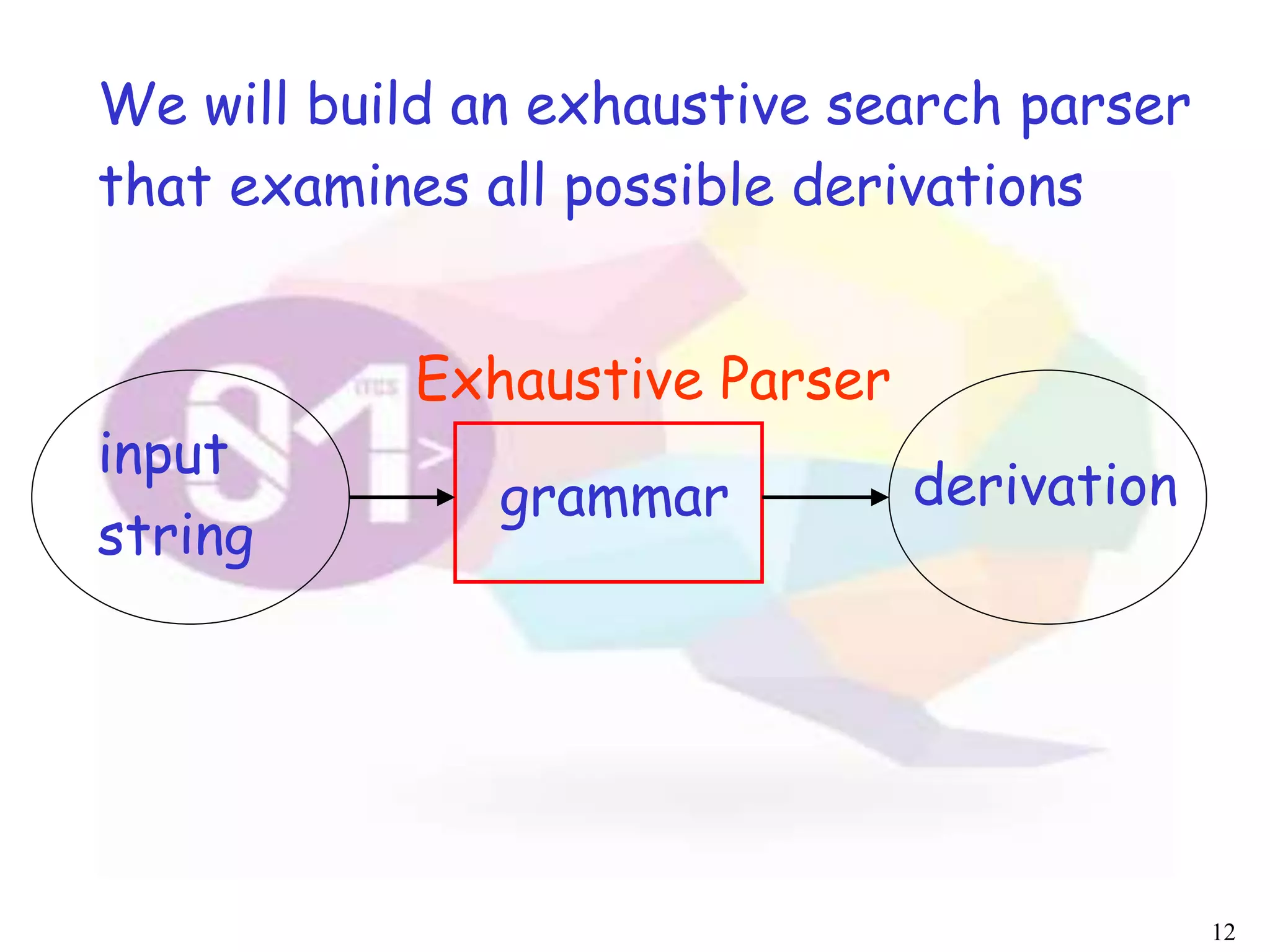
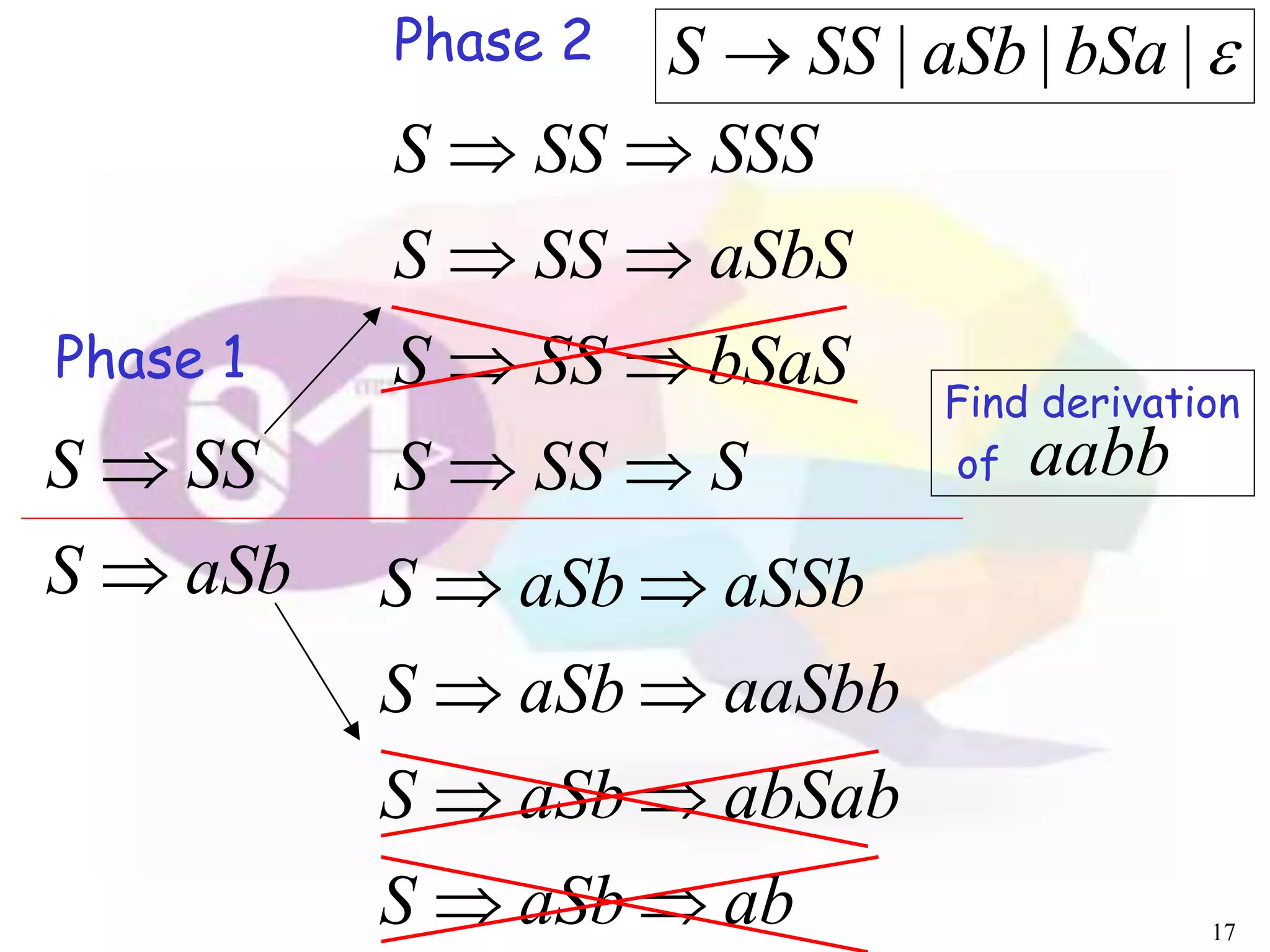
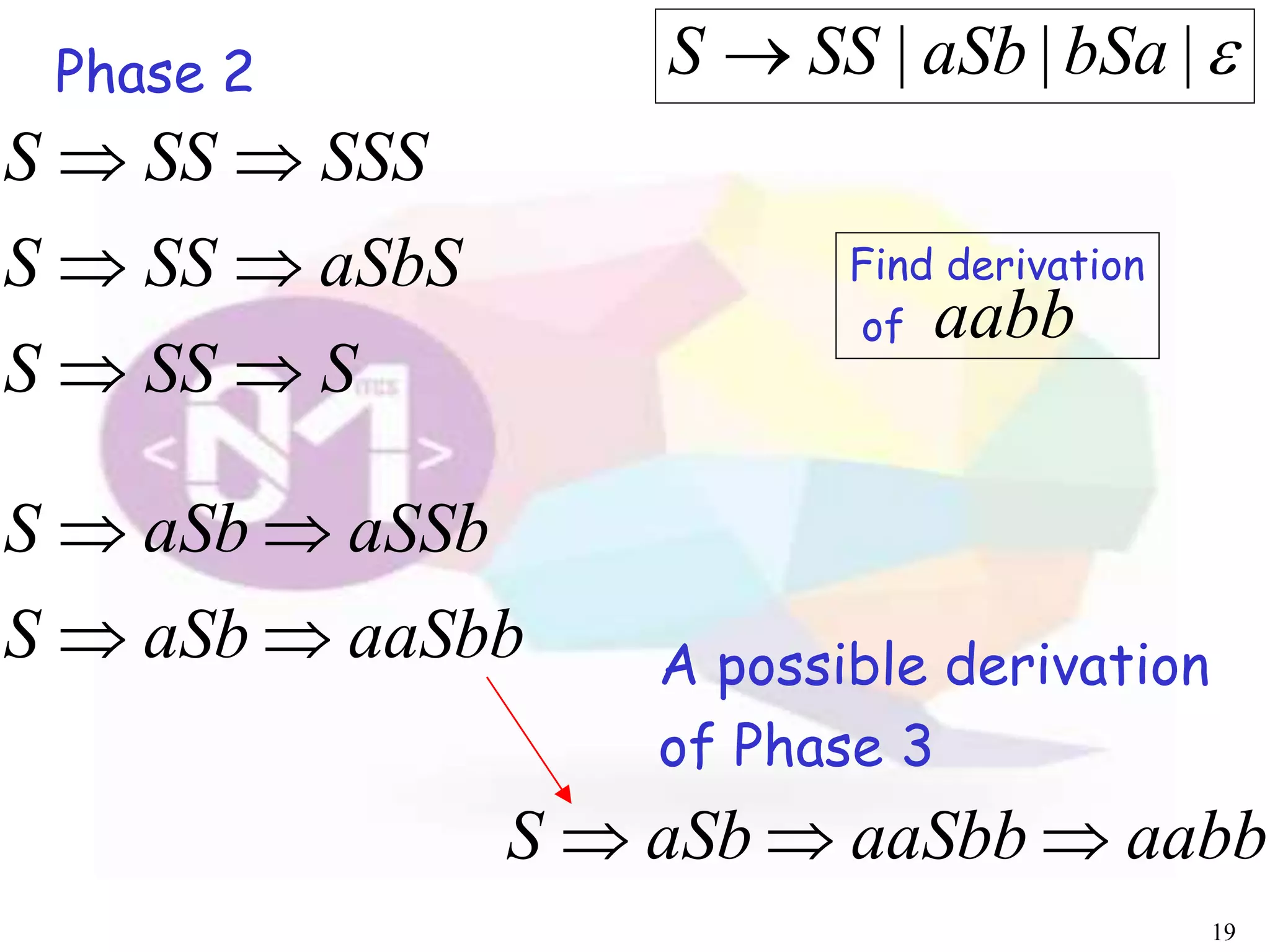
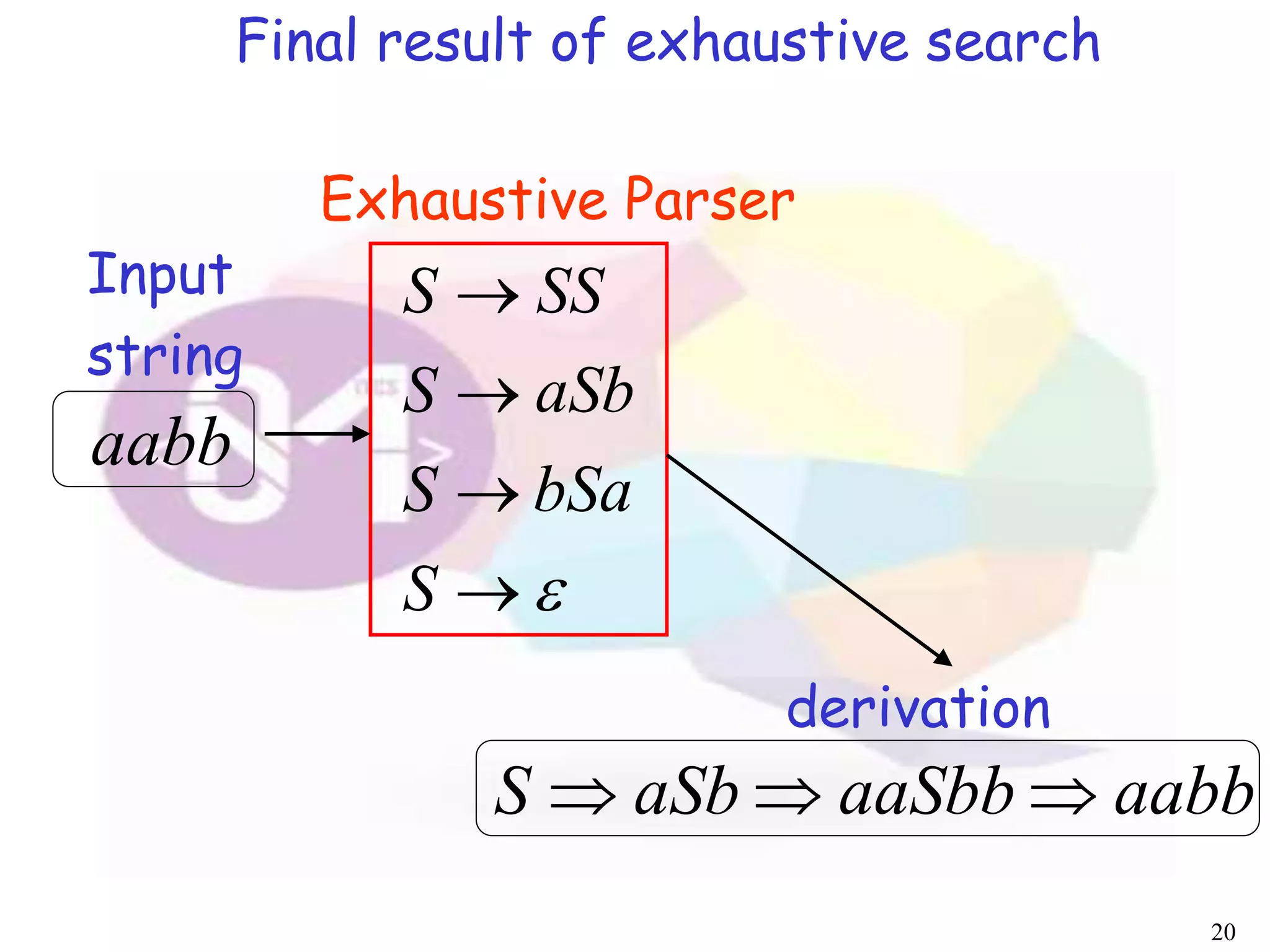
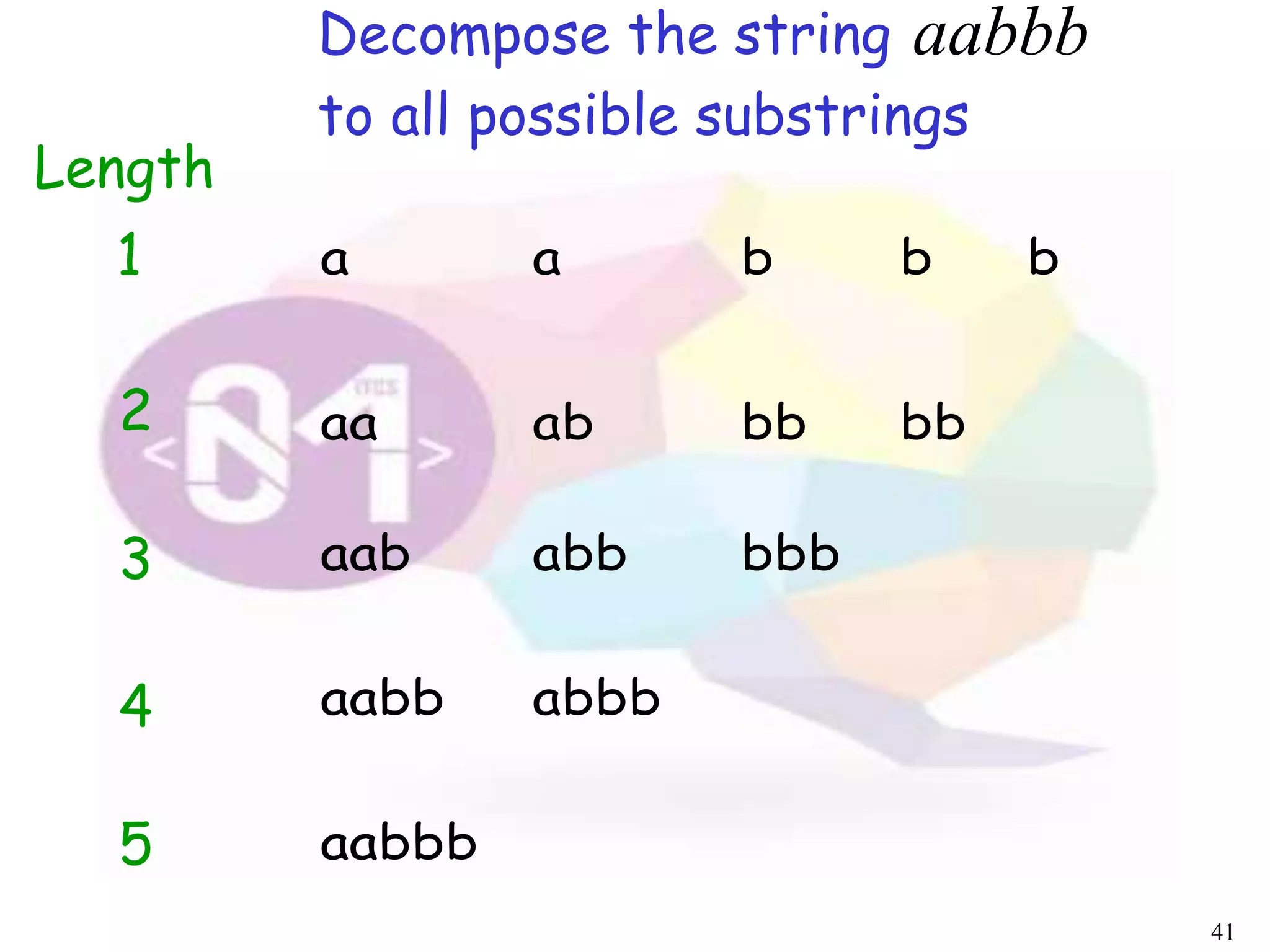
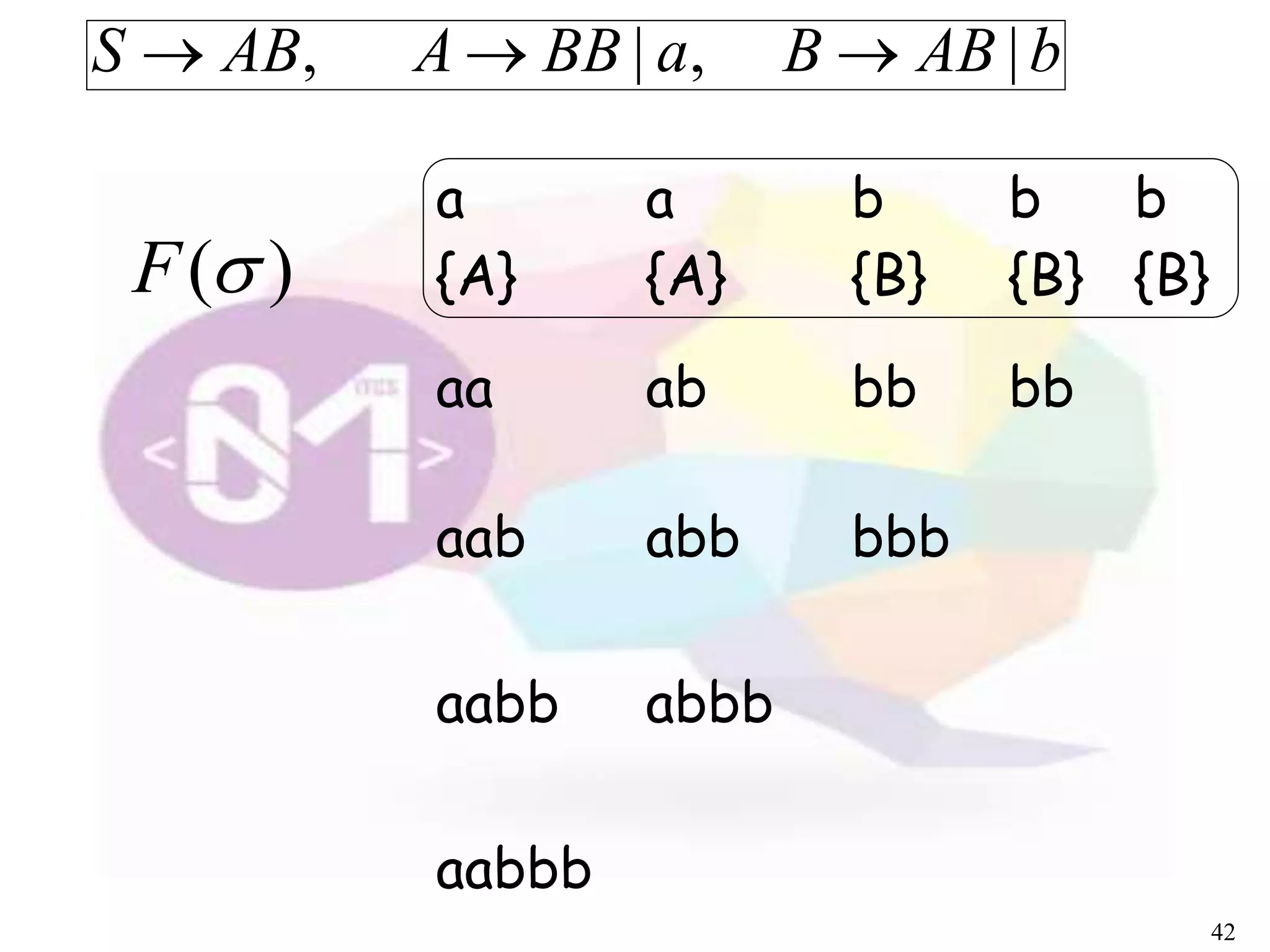
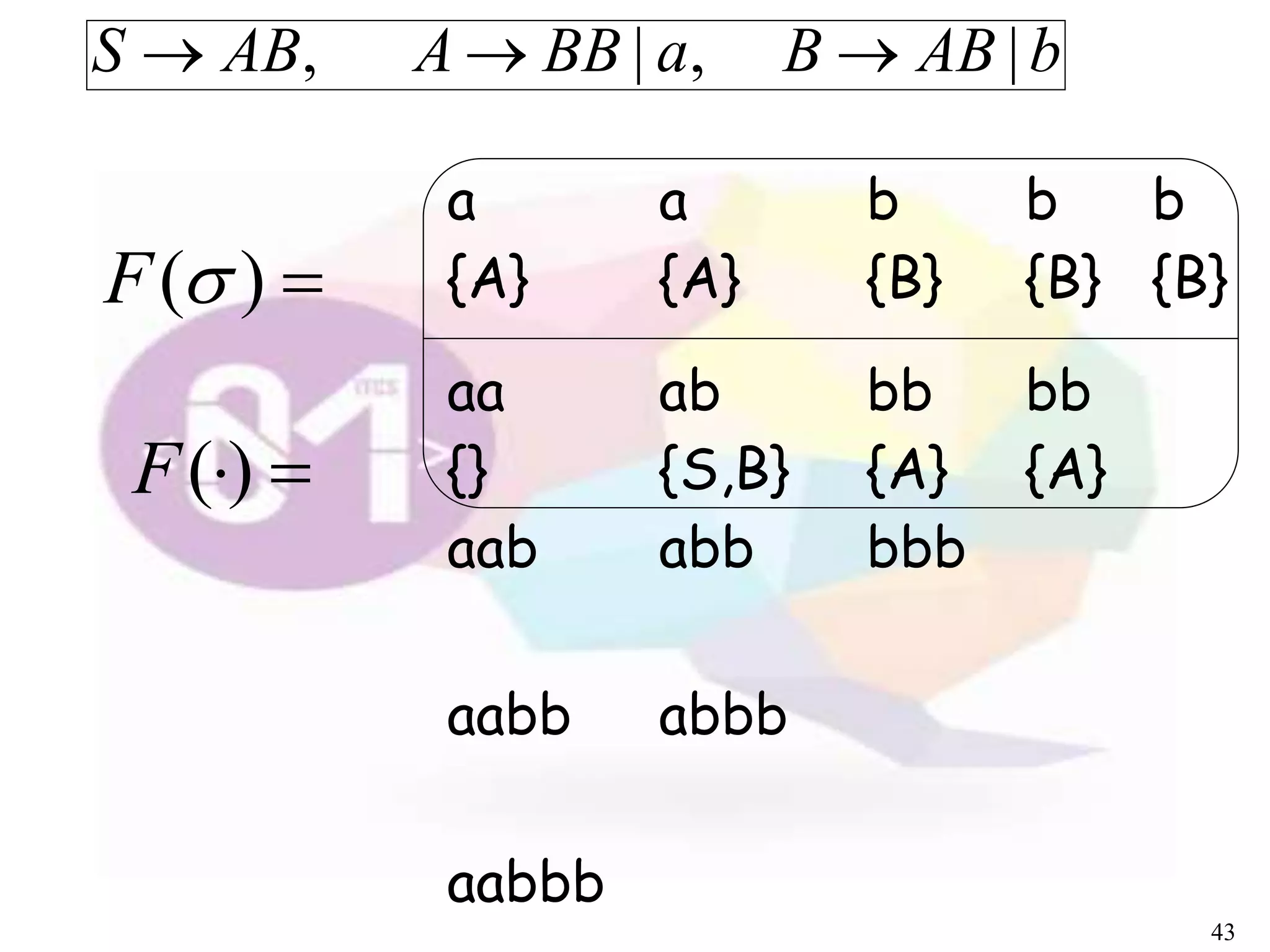
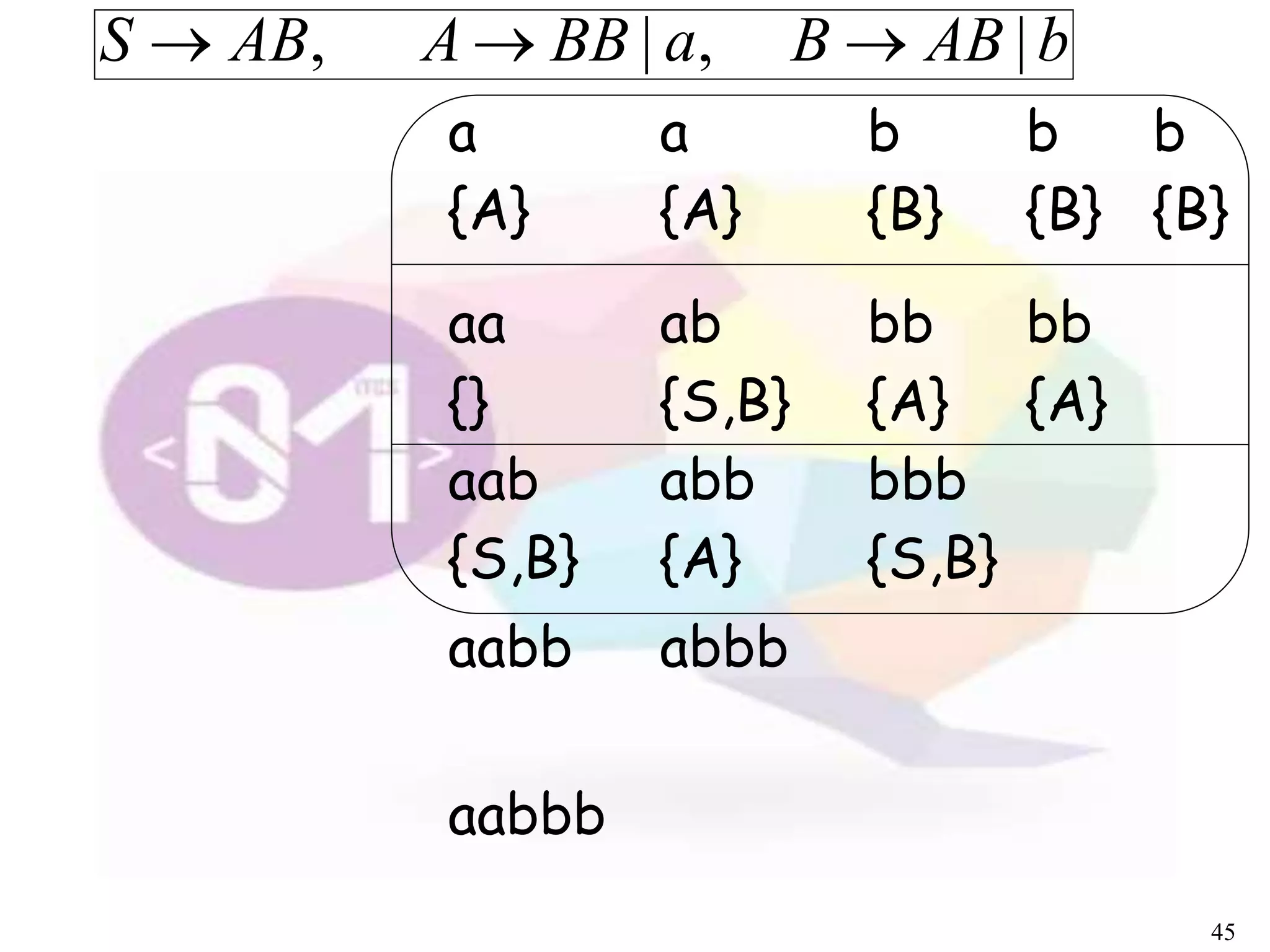
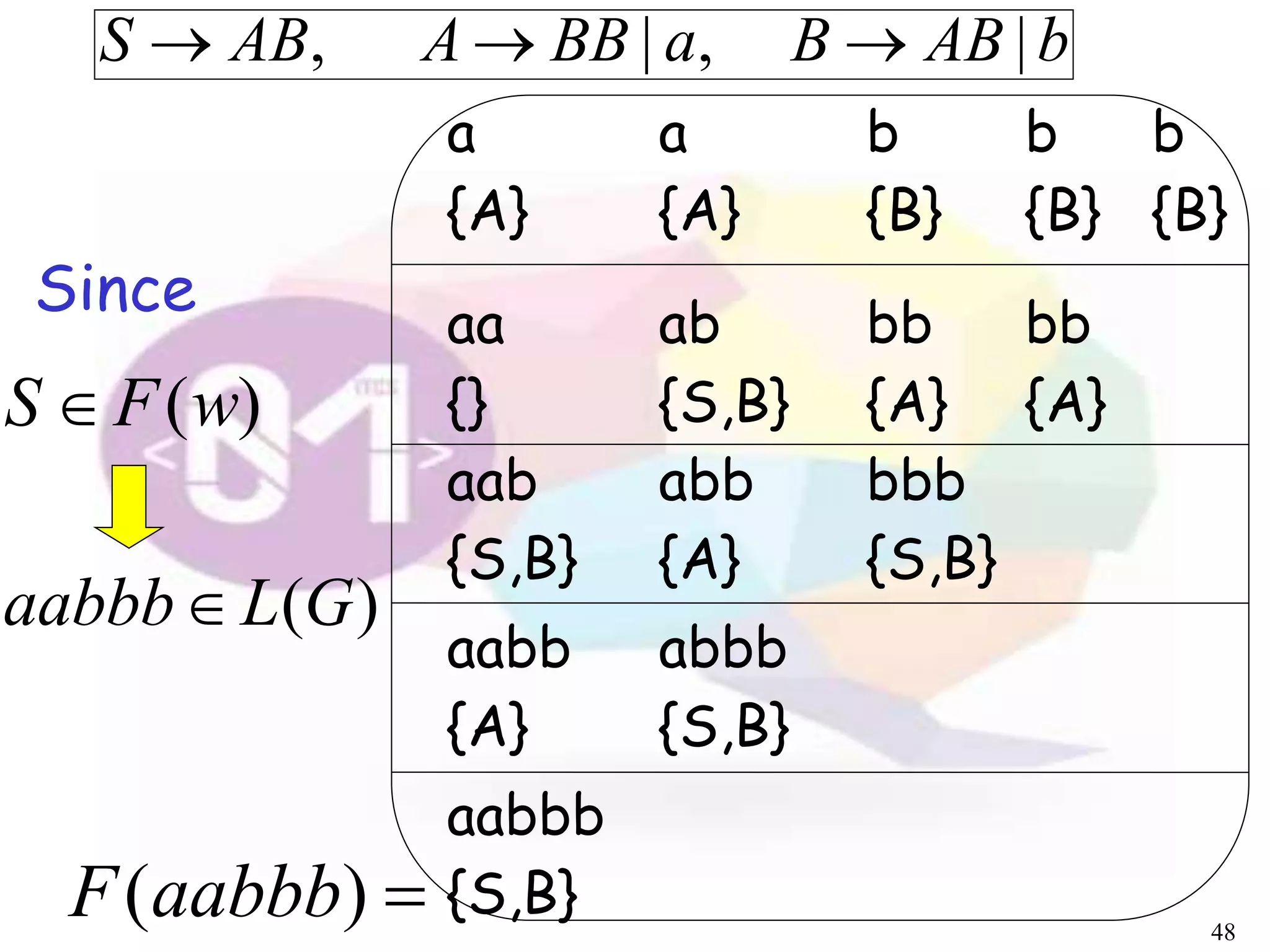
The document describes an algorithm for parsing context-free grammars called the CYK algorithm. It works by examining all possible decompositions of the input string into prefix-suffix pairs based on the grammar productions. It runs in O(n3) time, where n is the length of the input string, making it faster than an exhaustive search approach. The algorithm is demonstrated on an example grammar and string to show how it builds up the possible derivations in a bottom-up dynamic programming manner.

1. 1
Parsing
DISCLAIMER:
This video is optimized for HD large display using
patented and patent-pending “Nile Codec”, the first
Egyptian Video Codec for more information,
PLEASE check https://NileCodec.com
Also available as a PodCast

2. Copyright © 2020 Wael Badawy. All rights reserved
• This video is subject to copyright owned by Wael Badawy “WB”. Any reproduction
or republication of all or part of this video is expressly prohibited unless WB has
explicitly granted its prior written consent. All other rights reserved.
• This video is intended for education and information only and is offered AS IS,
without any warranty of the accuracy or the quality of the content. Any other use
is strictly prohibited. The viewer is fully responsible to verify the accuracy of the
contents received without any claims of costs or liability arising .
• The names, trademarks service marked as logos of WB or the sponsors appearing in
this video may not be used in any any product or service, without prior express
written permission from WB and the video sponsors
• Neither WB nor any party involved in creating, producing or delivering information
and material via this video shall be liable for any direction, incidental,
consequential, indirect of punitive damages arising out of access to, use or inability
to use this content or any errors or omissions in the content thereof.
• If you will continue to watch this video, you agree to the terms above and other
terms that may be available on http://nu.edu.eg & https://caiwave.net
2

4. 4
Compiler
Program File
v = 5;
if (v>5)
x = 12 + v;
while (x !=3) {
x = x - 3;
v = 10;
}
......
Add v,v,5
cmp v,5
jmplt ELSE
THEN:
add x, 12,v
ELSE:
WHILE:
cmp x,3
...
Machine Code

5. 5
Lexical
analyzer
parser
Compiler
Program
file
machine
code
Input String Output

6. 6
Lexical analyzer:
• Recognizes the lexemes of the
input program file:
Keywords (if, then, else, while,…),
Integers,
Identifiers (variables), etc
•It is built with DFAs (based on the
theory of regular languages)

7. 7
•Knows the grammar of the
programming language to be compiled
Parser:
•Constructs derivation (and derivation tree)
for input program file (input string)
•Converts derivation to machine code

8. 8
Example Parser
PROGRAM STMT_LIST
STMT_LIST STMT; STMT_LIST | STMT;
STMT EXPR | IF_STMT | WHILE_STMT
| { STMT_LIST }
EXPR EXPR + EXPR | EXPR - EXPR | ID
IF_STMT if (EXPR) then STMT
| if (EXPR) then STMT else STMT
WHILE_STMT while (EXPR) do STMT







9. 9
The parser finds the derivation
of a particular input file
10 + 2 * 5
Example
Parser
E -> E + E
| E * E
| INT
E => E + E
=> E + E * E
=> 10 + E*E
=> 10 + 2 * E
=> 10 + 2 * 5
Input string
derivation

10. 10
E => E + E
=> E + E * E
=> 10 + E*E
=> 10 + 2 * E
=> 10 + 2 * 5
derivation derivation tree
10
E
2 5
E E
E E
+
*
mult a, 2, 5
add b, 10, a
machine codeDerivation trees
are used to build
Machine code
a
b

11. 11
A simple (exhaustive) parser

12. 12
grammar
Exhaustive Parser
input
string
derivation
We will build an exhaustive search parser
that examines all possible derivations

13. 13
Example:
Exhaustive Parser
derivation




S
bSaS
aSbS
SSSInput string
?aabb
aabbFind derivation of string

14. 14
Exhaustive Search
||| bSaaSbSSS 
Phase 1:
All possible derivations of length 1
Find derivation
of aabb




S
bSaS
aSbS
SSS

15. 15
Find derivation
of aabb
Cannot possibly produce aabb
Phase 1:
||| bSaaSbSSS 




S
bSaS
aSbS
SSS

16. 16
aSbS
SSS


Phase 1
In Phase 2,
explore the next step
of each derivation
from Phase 1
||| bSaaSbSSS 

17. 17
Phase 2
aSbS
SSS

 SSSS
bSaSSSS
aSbSSSS
SSSSSS




Phase 1
abaSbS
abSabaSbS
aaSbbaSbS
aSSbaSbS




Find derivation
of aabb
||| bSaaSbSSS 

18. 18
Phase 2
SSSS
aSbSSSS
SSSSSS



aaSbbaSbS
aSSbaSbS


Find derivation
of aabb
In Phase 3 explore
all possible derivations
||| bSaaSbSSS 

19. 19
Phase 2
SSSS
aSbSSSS
SSSSSS



aaSbbaSbS
aSSbaSbS


A possible derivation
of Phase 3
aabbaaSbbaSbS 
Find derivation
of aabb
||| bSaaSbSSS 

20. 20
Final result of exhaustive search
Exhaustive Parser
derivation




S
bSaS
aSbS
SSSInput
string
aabb
aabbaaSbbaSbS 

21. 21
( -productions)
Suppose that the grammar does not have
productions of the form
A
BA  (unit productions)

Time Complexity

22. Since the are no -productions
22
wxxxS k  21
|||| wxi 
For any derivation of a
string of terminals )(GLw 
it holds that for all i


23. 23
Since the are no unit productions
1. At most derivation steps are needed
to produce a string with at most
variables
||w
jx ||w
2. At most derivation steps are needed
to convert the variables of to the
string of terminals
||w
jx
w

24. 24
Therefore, at most derivation
steps are required to produce
||2 w
w
The exhaustive search requires at most
||2 w phases

25. 25
Possible derivation choices
to be examined in phase 1: k
kSuppose the grammar has productions
at most

26. 26
Choices for phase 2: at most
2
kkk 
Choices of
phase 1
Number of
Productions
Choices for phase i: at most
ii
kkk  )1(
Choices of
phase i-1
Number of
Productions
In General

27. 27
Total exploration choices for string :w
)( ||2||22 ww
kOkkk  
Extremely bad!!!
phase 1 phase 2 phase 2|w|
Exponential to the string length

28. 28
Faster Parsers

29. 29
There exist faster parsing algorithms
for specialized grammars
S-grammar: avA 
Symbol String of variables
),( X
appears once in a production
Each pair of variable, terminal
(a restricted version of Greinbach Normal form)
wX 

30. 30
S-grammar example:
cS
bSSS
aSS



abccabcSabSSaSS 
Each string has a unique derivation

31. 31
In the exhaustive search parsing
there is only one choice in each phase
For S-grammars:
Total steps for parsing string :w || w
Steps for a phase: 1

32. 32
For general context-free grammars:
Next, we give a parsing algorithm
that parses a string in timew )|(| 3
wO
(this time is very close to the worst case
optimal since parsing can be used to solve
the matrix multiplication problem)

33. 33
The CYK Parsing Algorithm
Input: • Arbitrary Grammar
in Chomsky Normal Form
G
• String
Output: Determine if )(GLw
w
Number of Steps: )|(| 3
wO
Can be easily converted to a Parser

34. 34
Basic Idea
Denote by the set of variables
that generate a string
)(wF
w
Consider a grammar
In Chomsky Normal Form
G
)(wFX  wX
*
if

35. 35
Suppose that we have computed )(wF
Check if :)(wFS 
YES
NO
)(GLw 
)(GLw 
)(
*
wS 

36. 36
and there is production
uvw 
)(uFX 
)(wF can be computed recursively:
)(vFY 
XYH 
Then )(wFH 
prefix suffix
If
)(
*
vY )(
*
uX 
and
)(
**
wuvuYXYH 
Write

37. 37
Examine all prefix-suffix
decompositions of w
1||1 
 w
vuw
2||2 
 w
vuw
11||
vuw w 

1
2
|w|-1
Length Set of Variables
that generate w
1H
2H
1|| wH
1||21)(  wHHHwF Result:

38. 38
At the basis of the recursion
we have strings of length 1
}symbolgeneratethatVariables{)(  F
symbol X
Very easy to find

39. 39
The whole algorithm can be implemented
with dynamic programming:
Remark:
First compute for smaller
substrings and then use this
to compute the result for larger
substrings of
)(wF 
w 
w

40. 40
• Grammar :G
bABB
aBBA
ABS
|
|



• Determine if )(GLaabbbw 
Example:

41. 41
a a b b b
aa ab bb bb
aab abb bbb
aabb abbb
aabbb
aabbbDecompose the string
to all possible substrings
Length
1
2
3
4
5

42. a
{A}
a
{A}
b
{B}
b
{B}
b
{B}
aa ab bb bb
aab abb bbb
aabb abbb
aabbb
42
bABBaBBAABS |,|, 
)(F

43. a
{A}
a
{A}
b
{B}
b
{B}
b
{B}
aa
{}
ab
{S,B}
bb
{A}
bb
{A}
aab abb bbb
aabb abbb
aabbb
43
bABBaBBAABS |,|, 
)(F
)(F

44. 44
)(aaF
}{)( AaF 
AAX There is no production of form
aaprefix suffix
}{)( AaF 
bABBaBBAABS |,|, 
Thus, {})( aaF
)(abF
}{)( AaF 
ABX There are two productions of form
abprefix suffix
}{)( BbF 
Thus, },{)( BSabF 
ABBABS  ,

45. a
{A}
a
{A}
b
{B}
b
{B}
b
{B}
aa
{}
ab
{S,B}
bb
{A}
bb
{A}
aab
{S,B}
abb
{A}
bbb
{S,B}
aabb abbb
aabbb
45
bABBaBBAABS |,|, 

46. 46
)(aabF
}{)( AaF 
ASX There is no production of form
aabprefix suffix
},{)( BSabF 
bABBaBBAABS |,|, 
ABX 
ABBABS  ,
There are 2 productions of form
Decomposition 1
},{1 BSH 

47. 47
)(aabF
{})( aaF
BX There is no production of form
aabprefix suffix
}{)( BbF 
bABBaBBAABS |,|, 
Decomposition 2
}{2 H
},{}{},{)( 21 BSBSHHaabF 

48. a
{A}
a
{A}
b
{B}
b
{B}
b
{B}
aa
{}
ab
{S,B}
bb
{A}
bb
{A}
aab
{S,B}
abb
{A}
bbb
{S,B}
aabb
{A}
abbb
{S,B}
aabbb
{S,B} 48
bABBaBBAABS |,|, 
)(aabbbF
)(GLaabbb
)(wFS 
Since

49. 49
Approximate time complexity:
)|(||)||(| 32
wOwwO 
Number of
substrings
Number of
Prefix-suffix
decompositions
for a string

50. Questions
Leave a comment below
or
Email: Badawy@caiwave.net
50