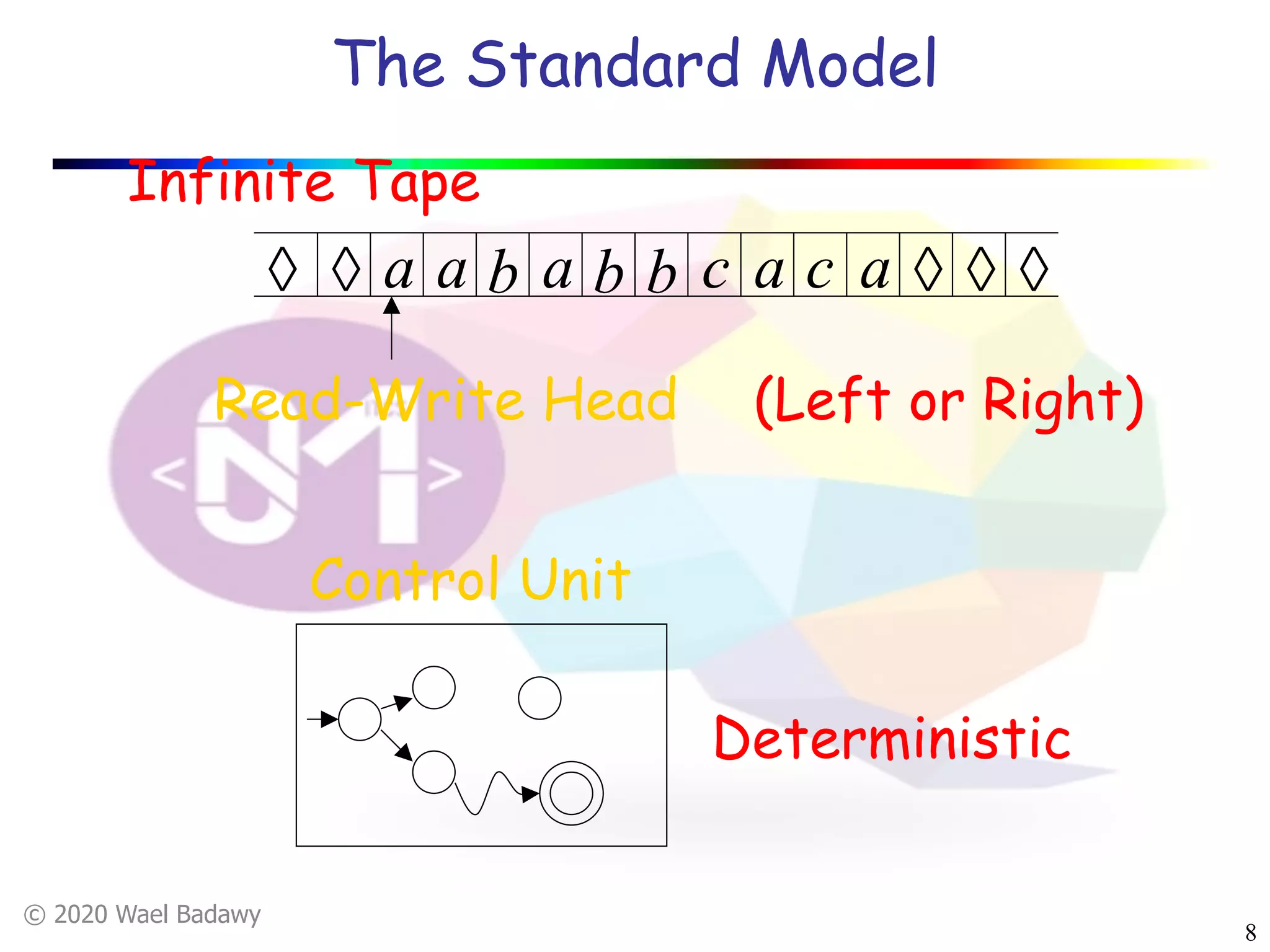
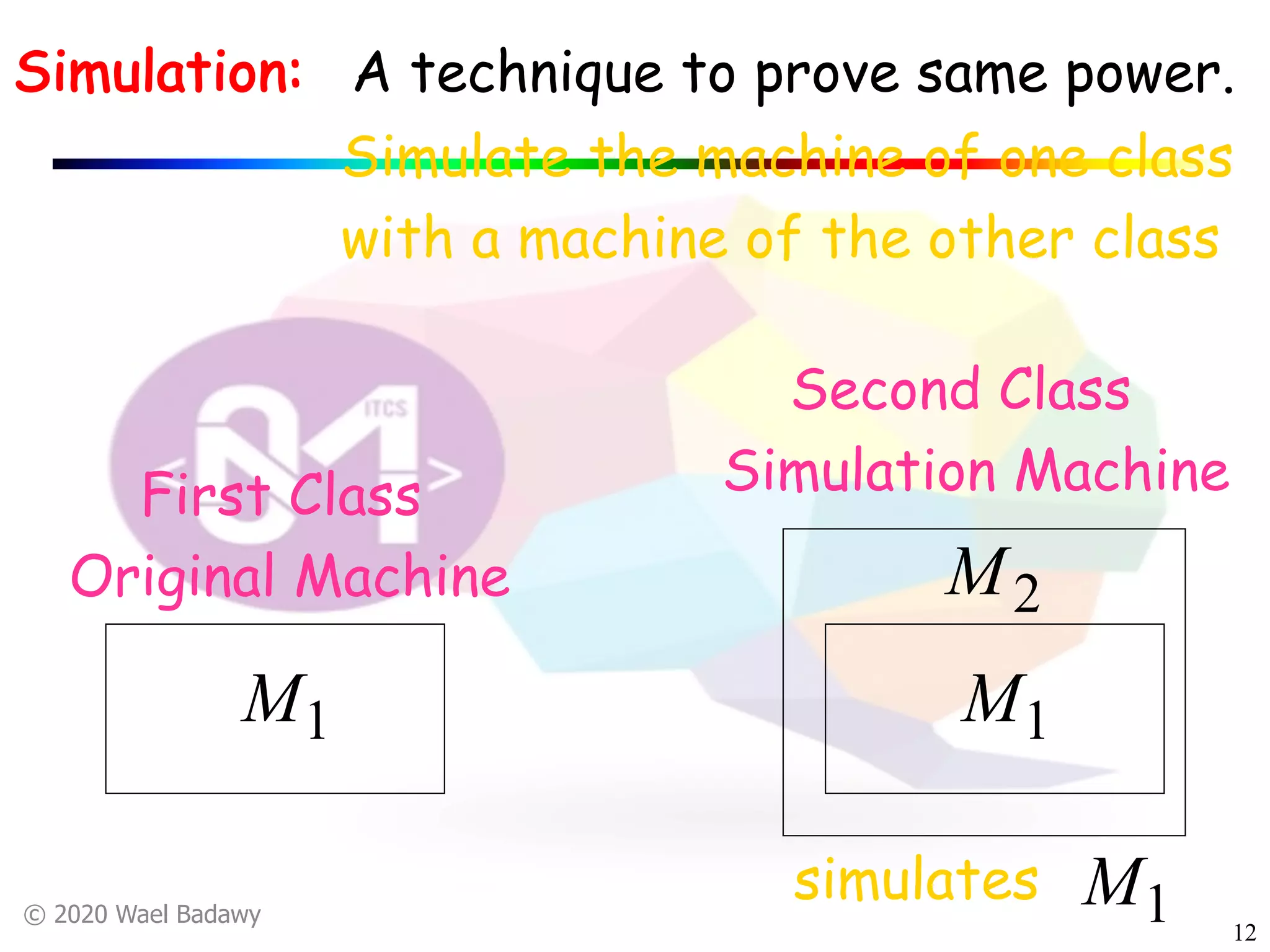
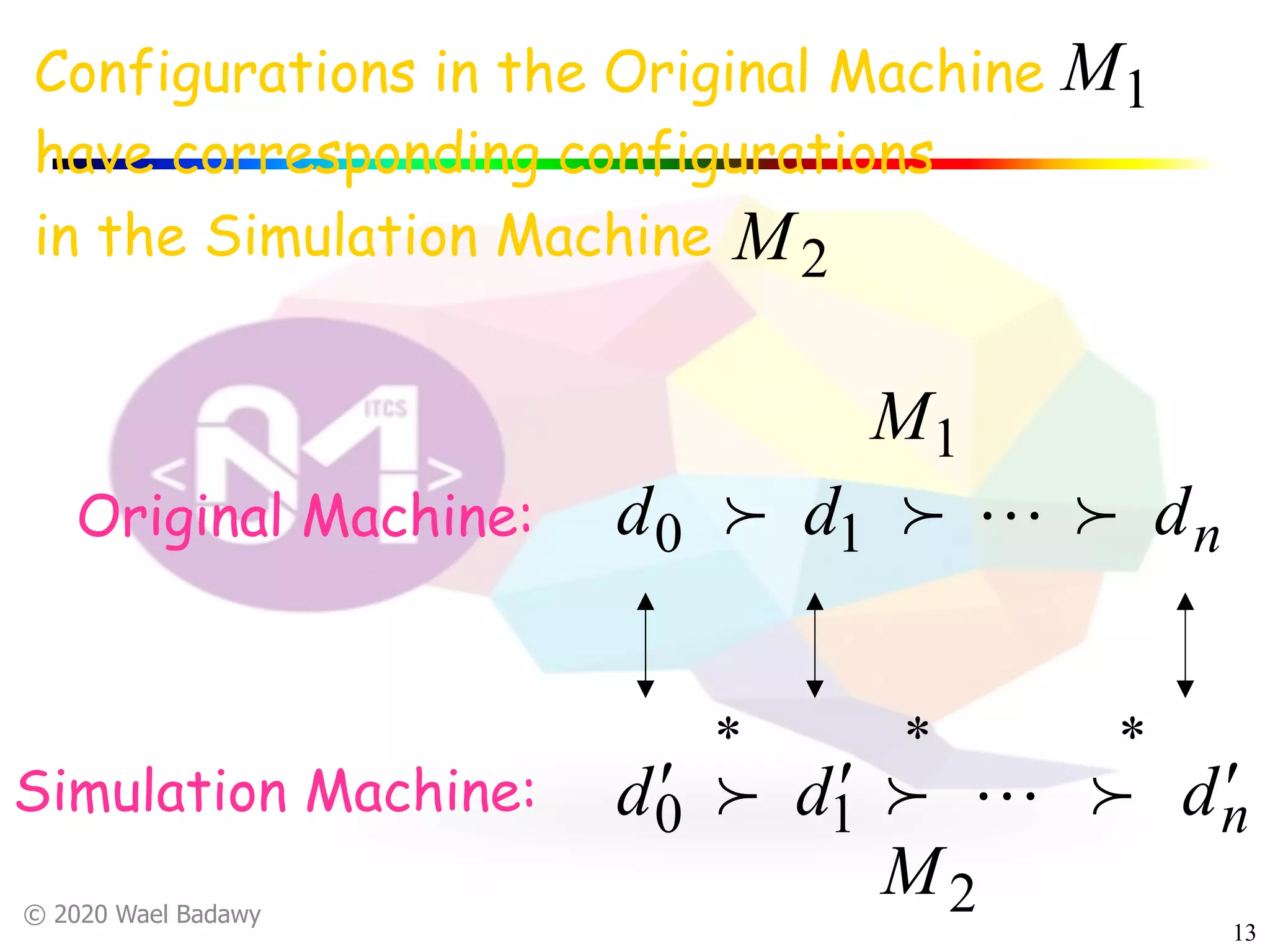
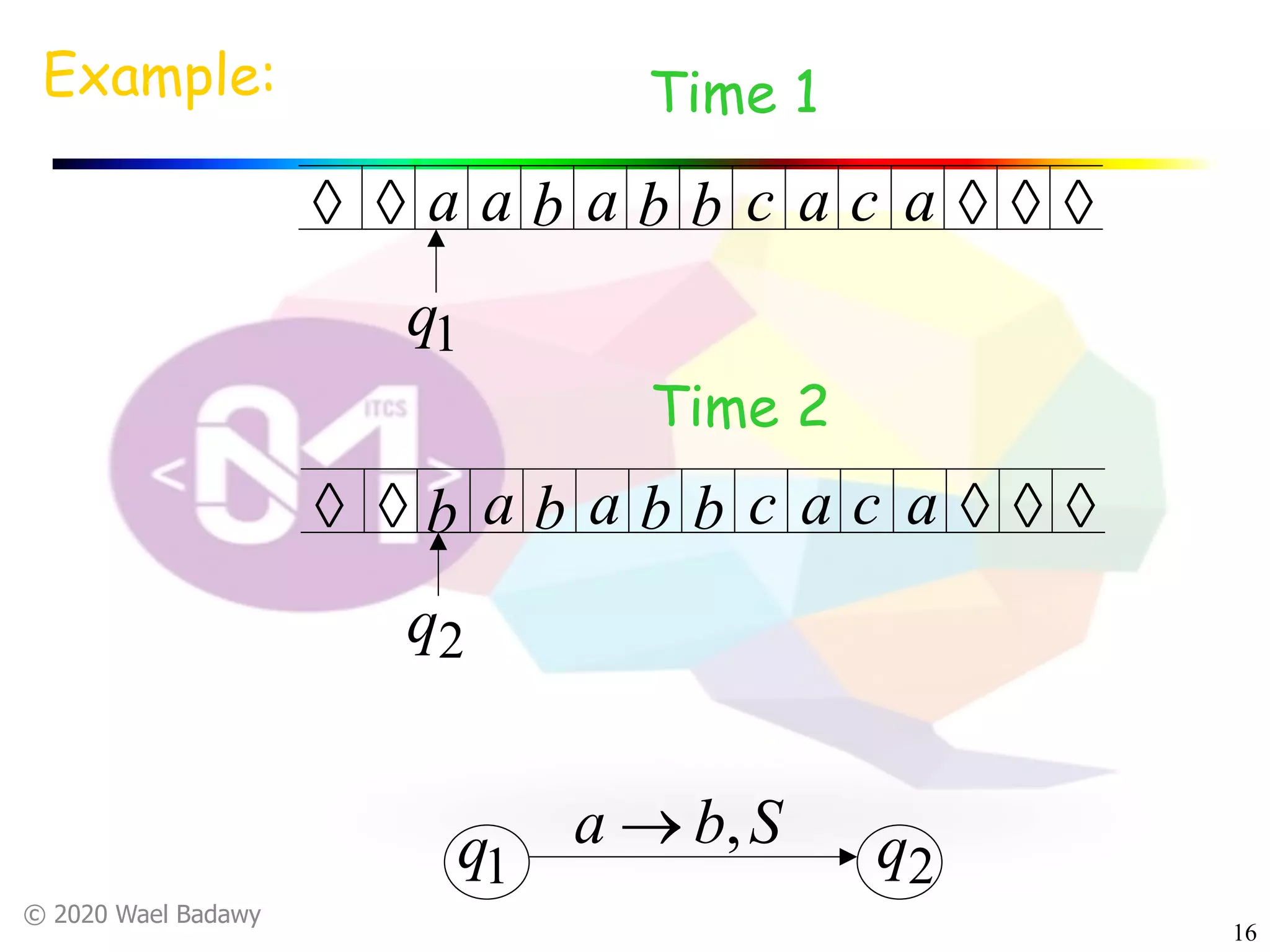
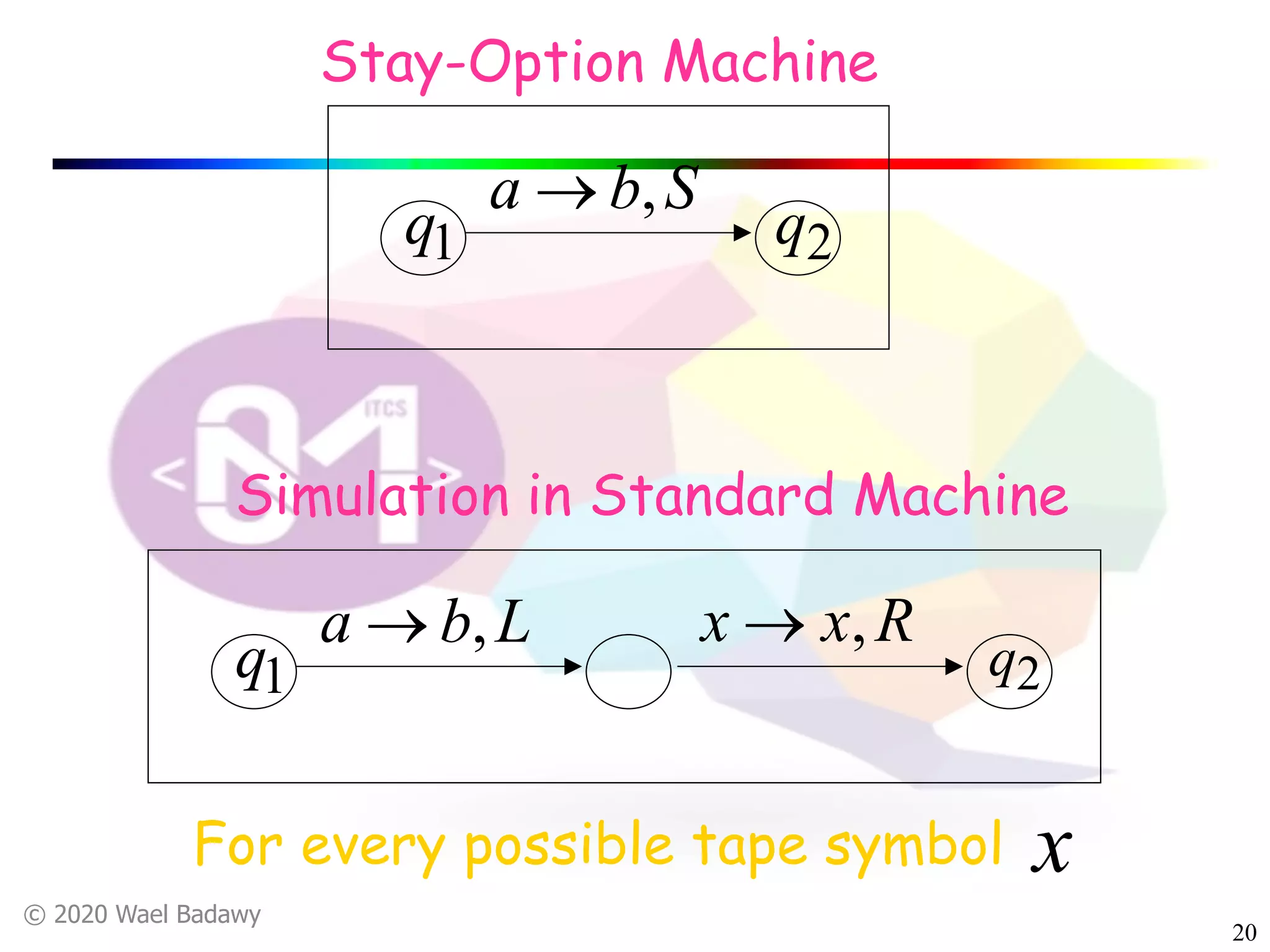
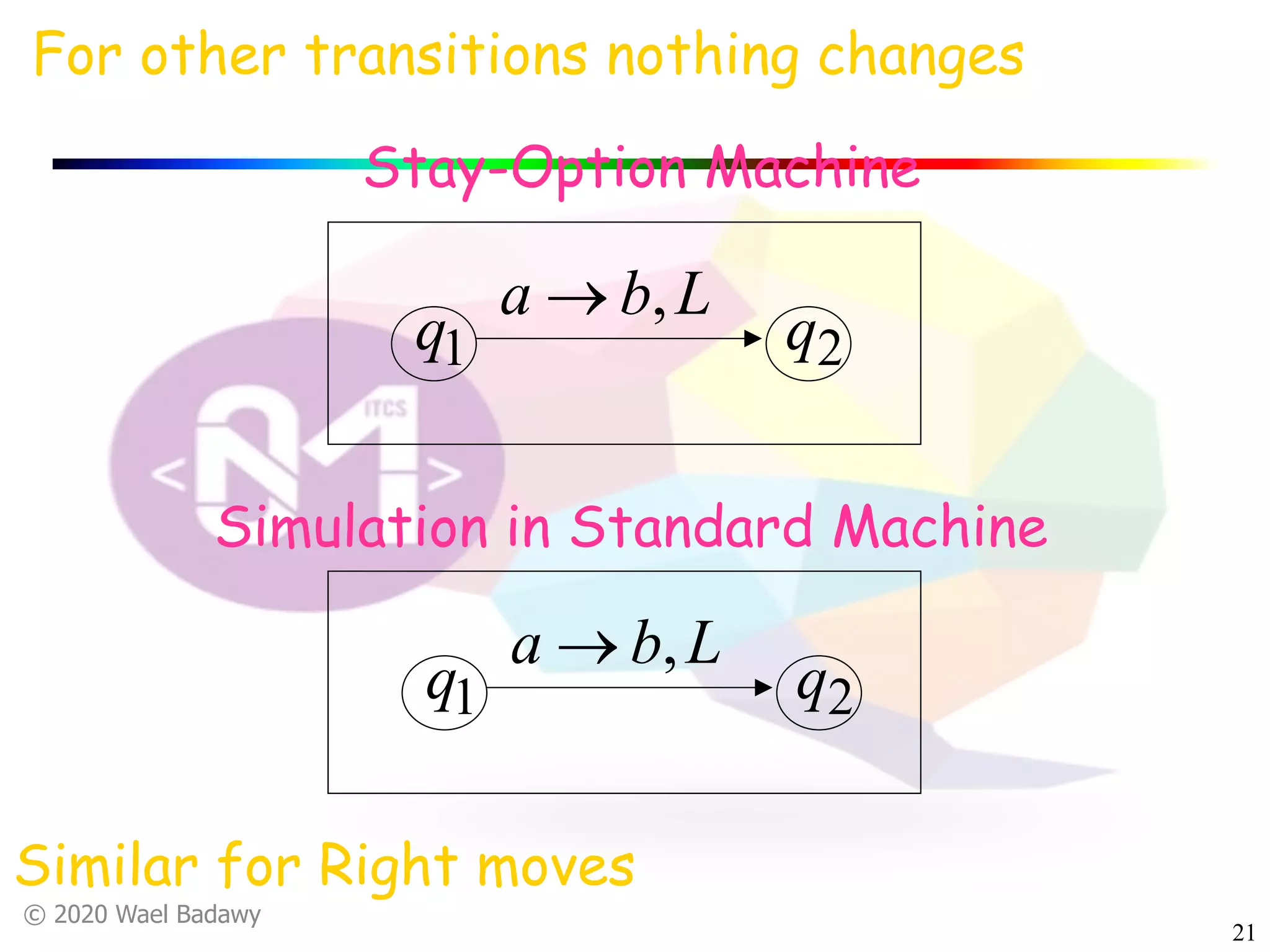
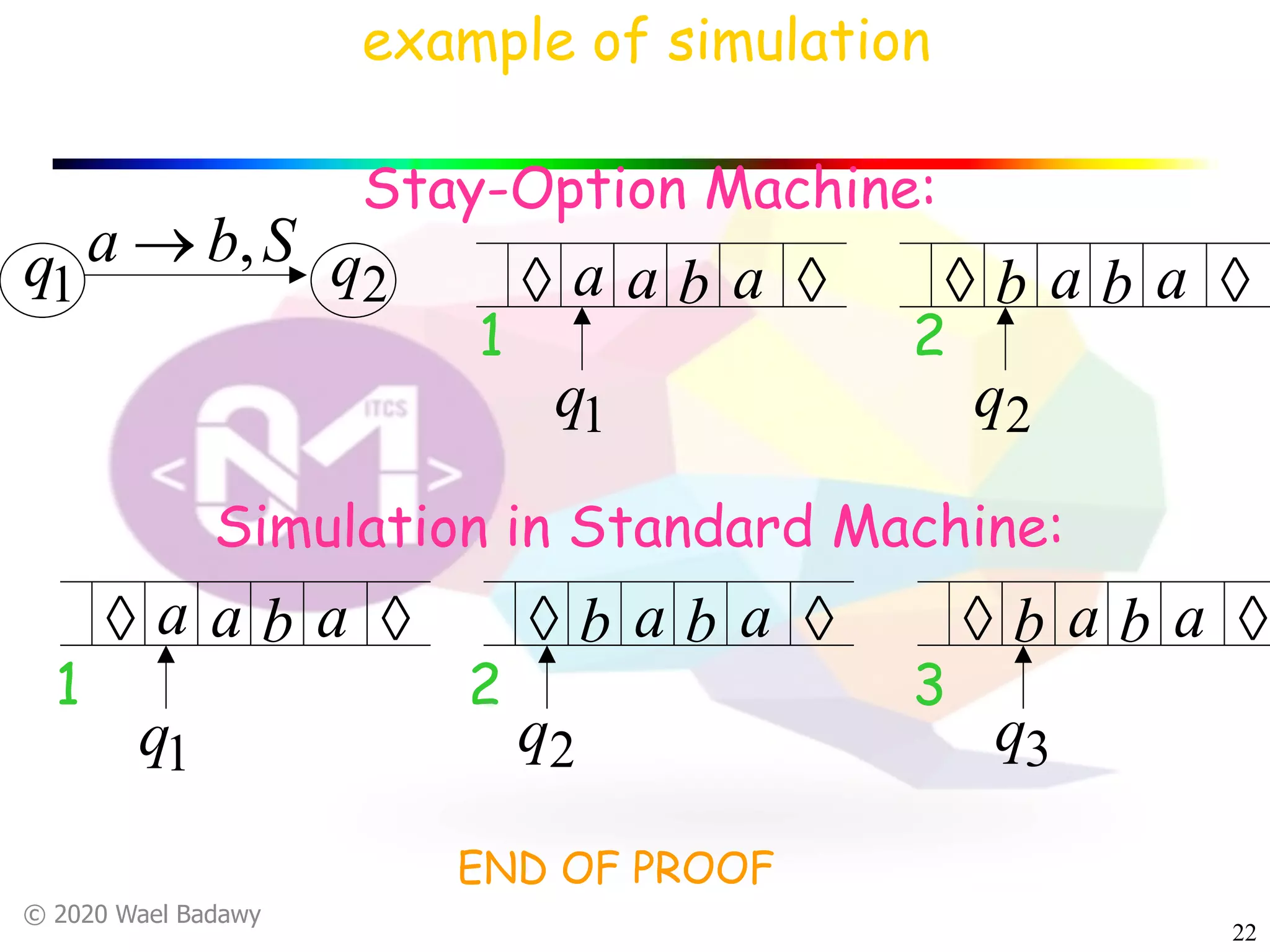
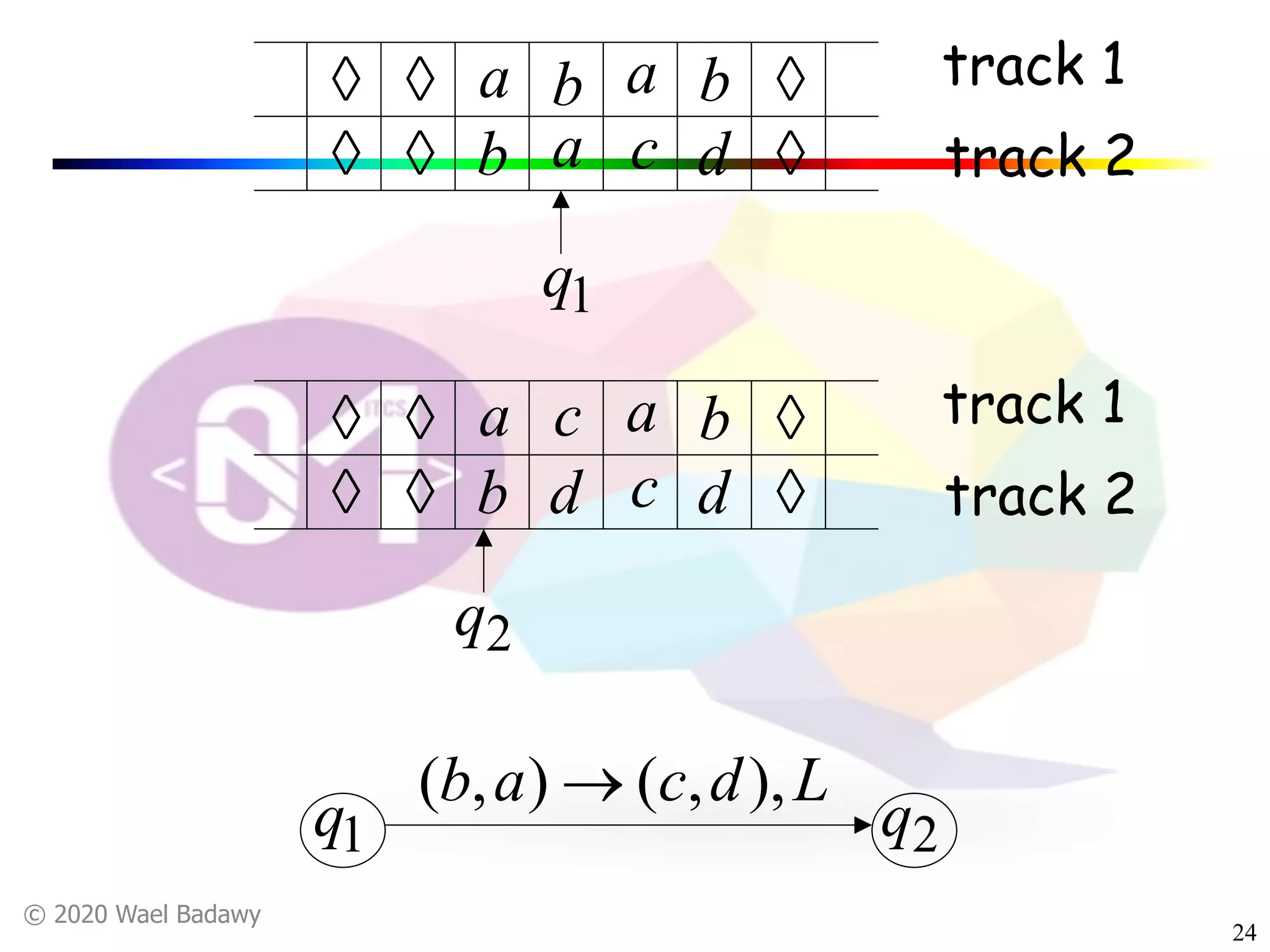
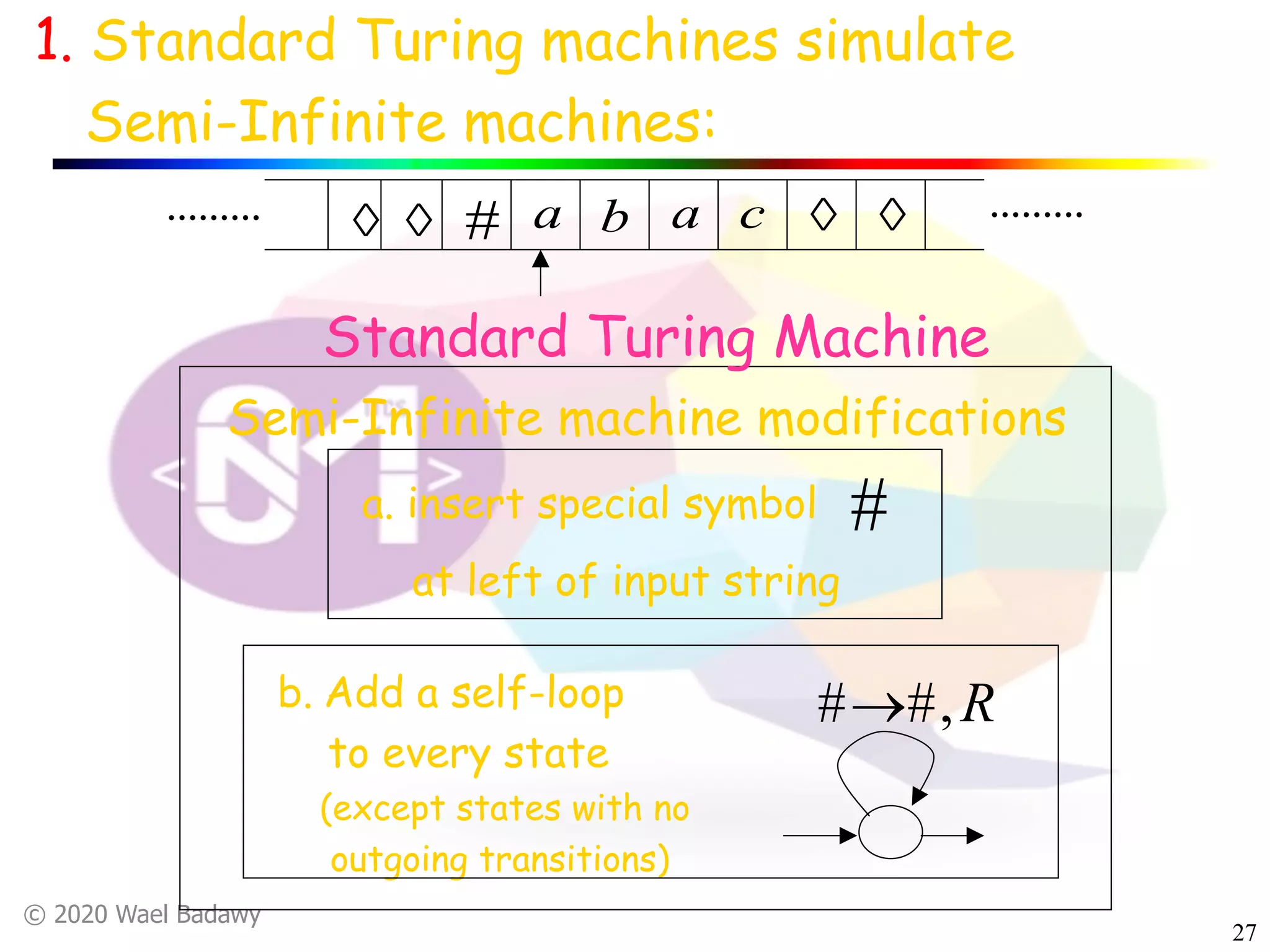
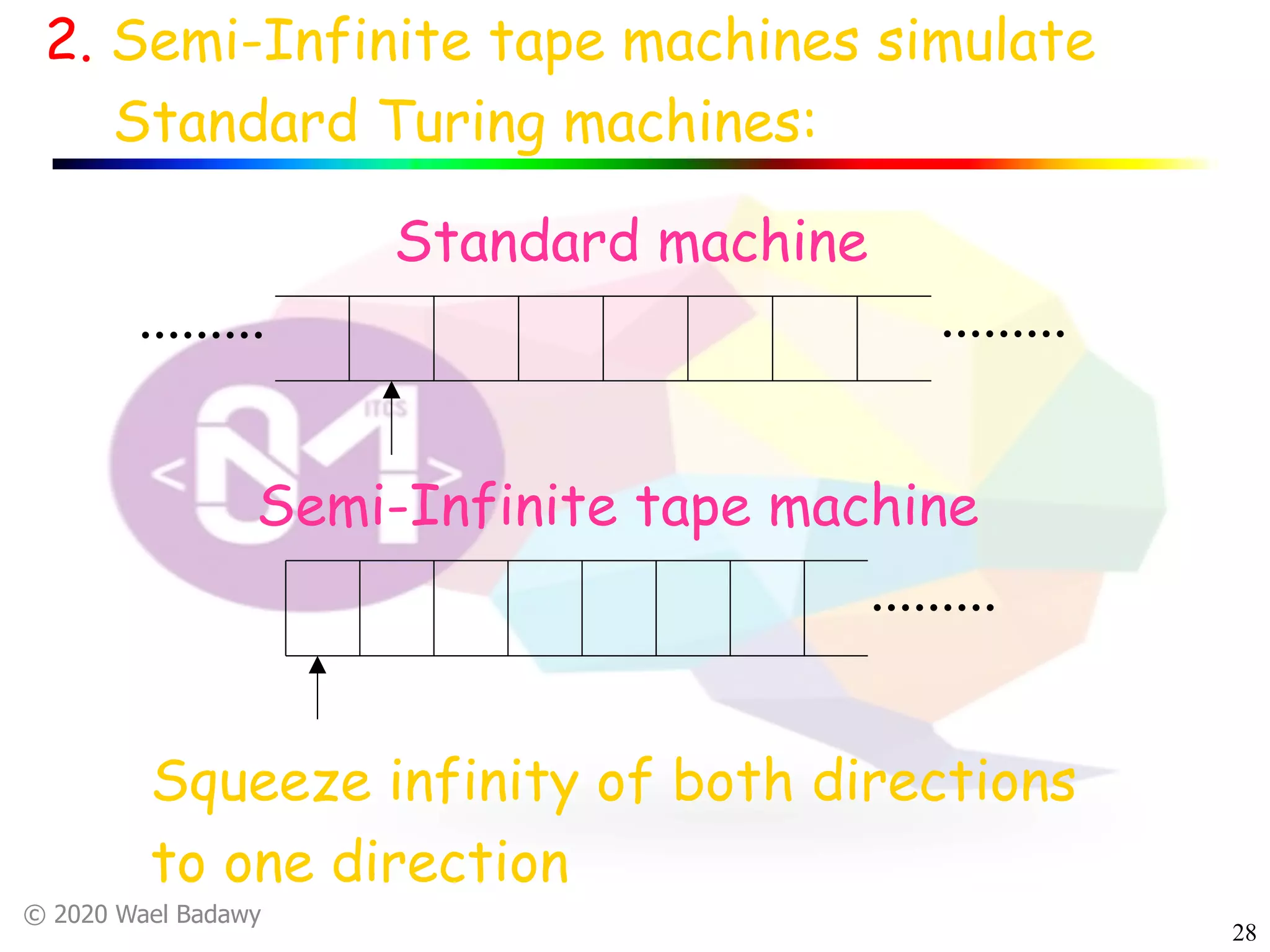
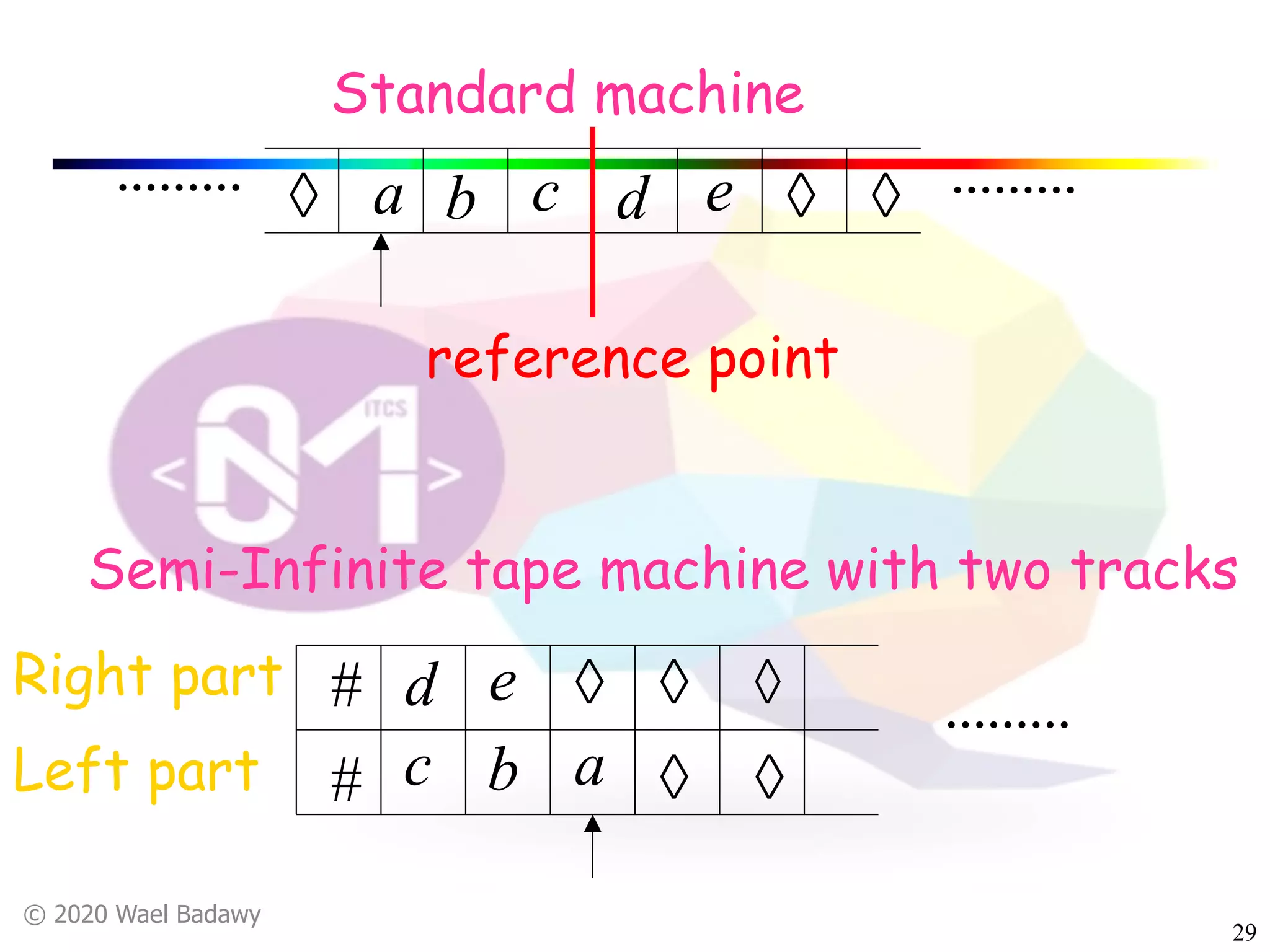
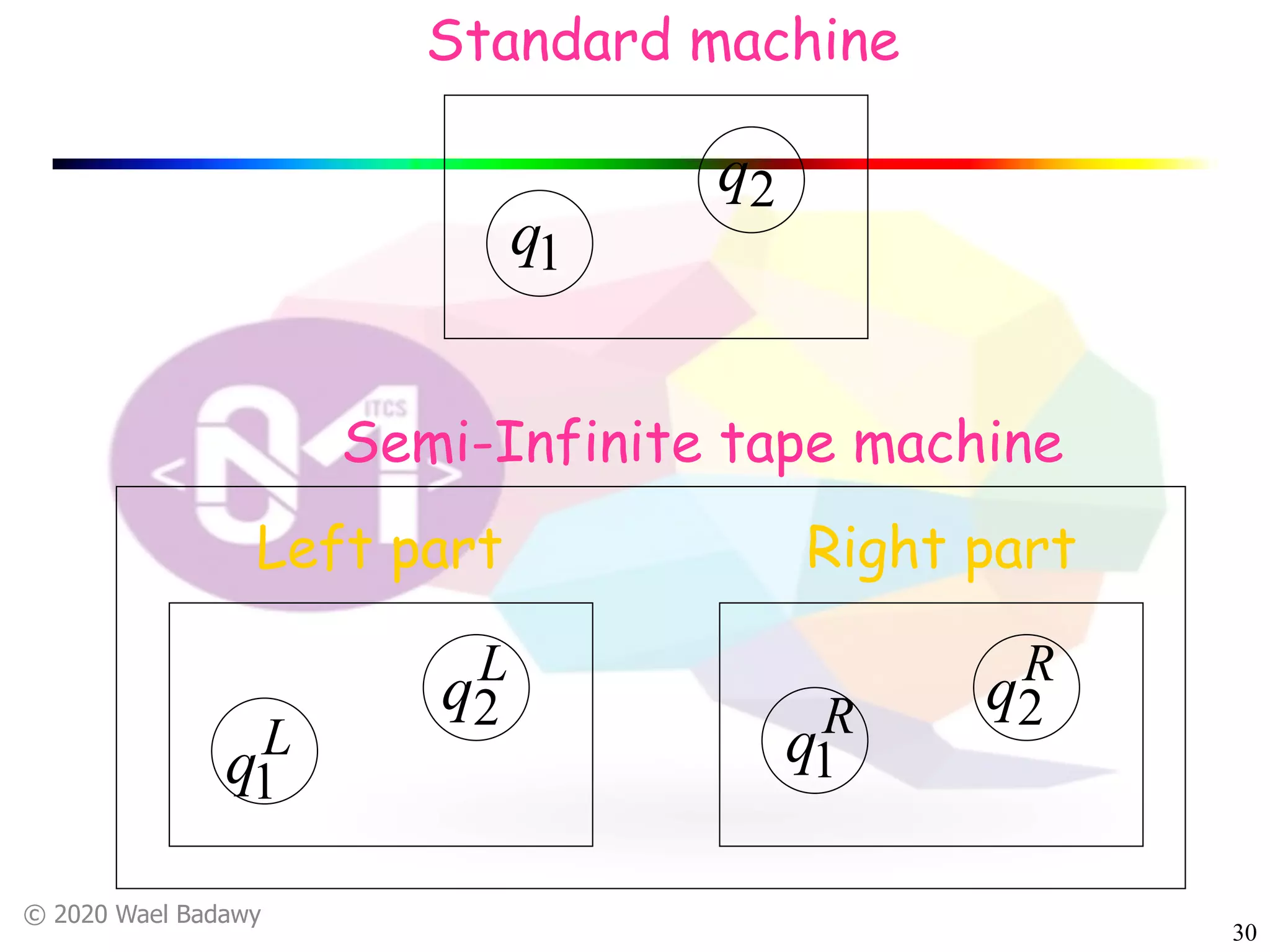
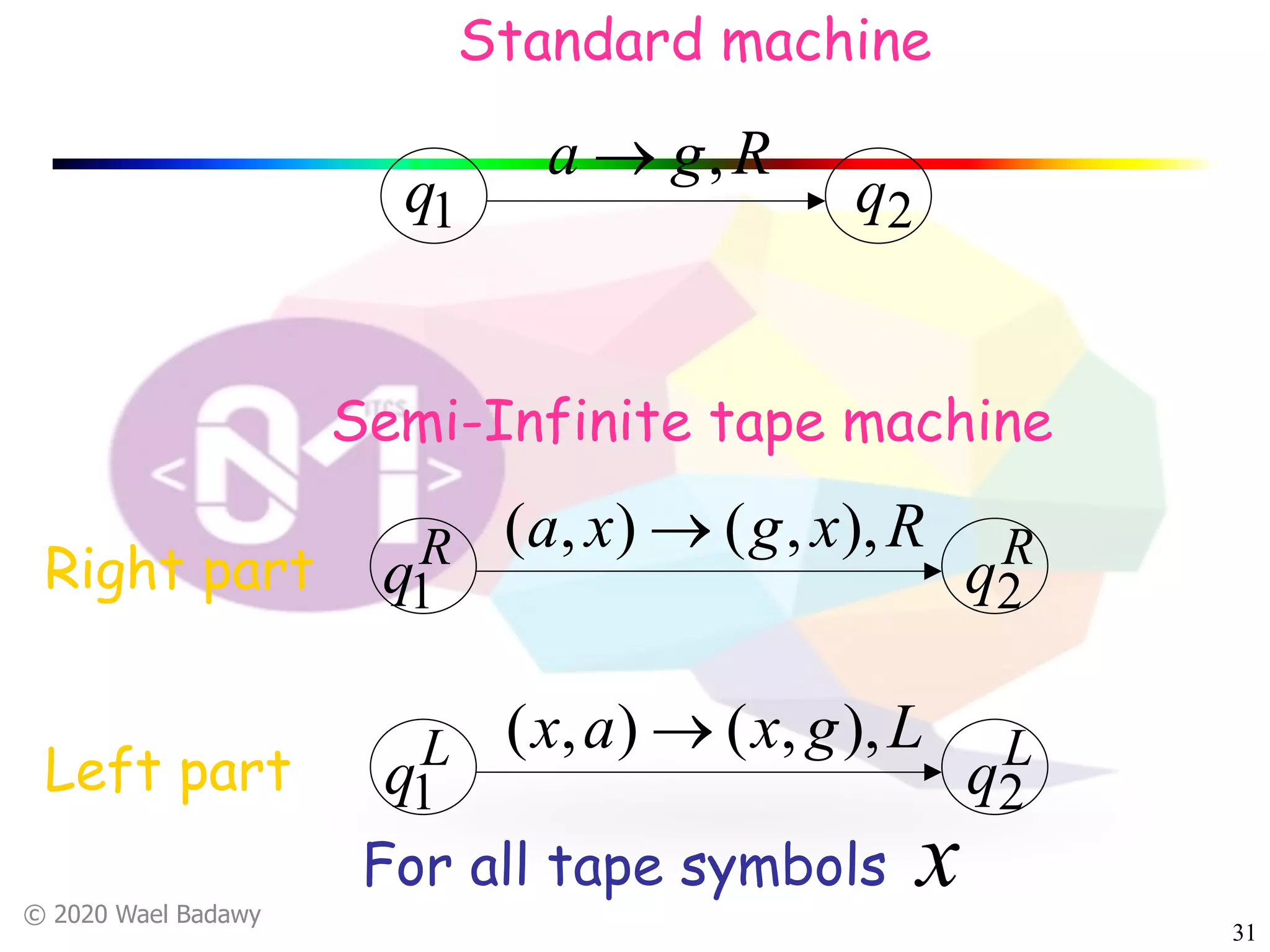
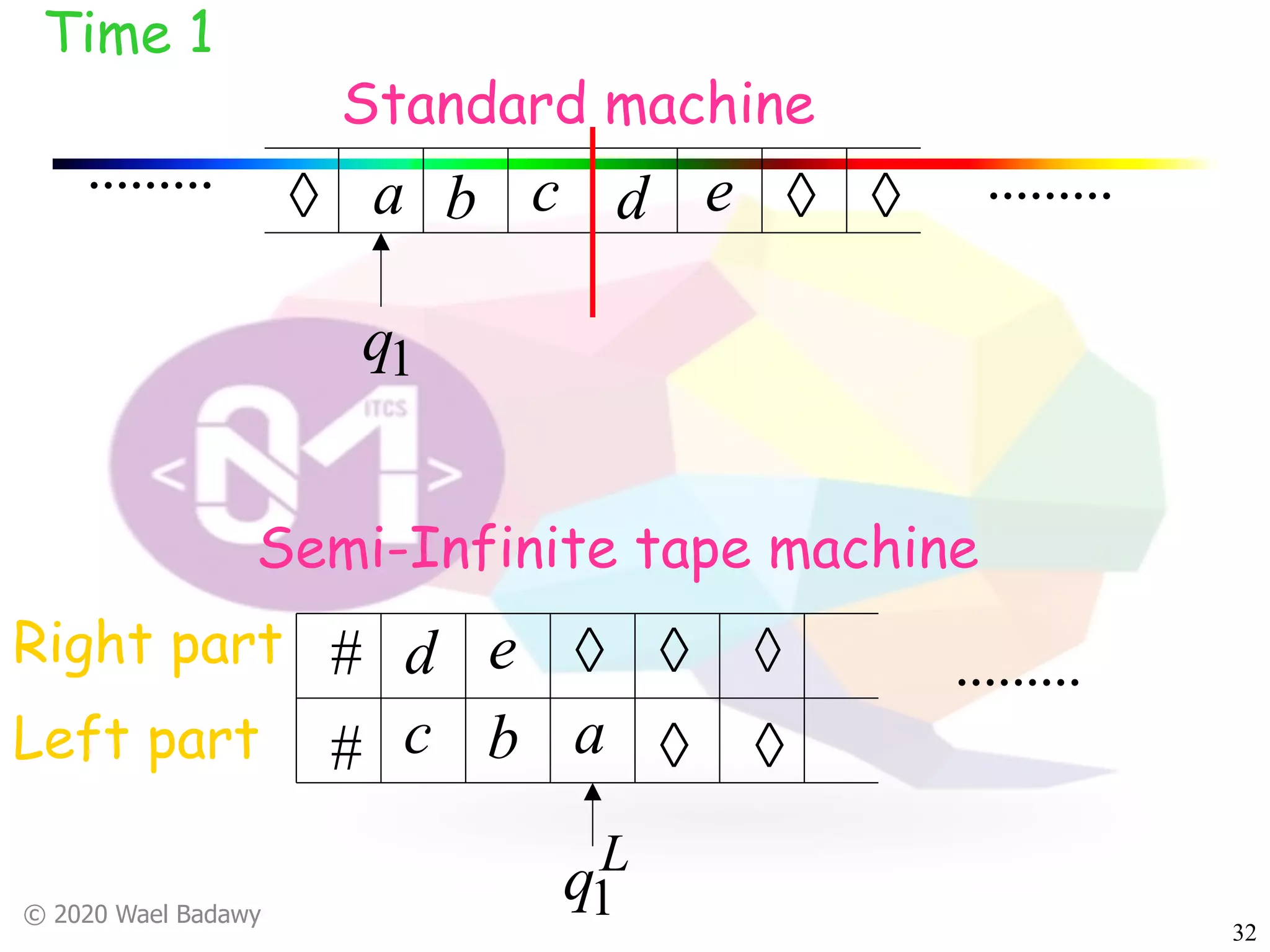
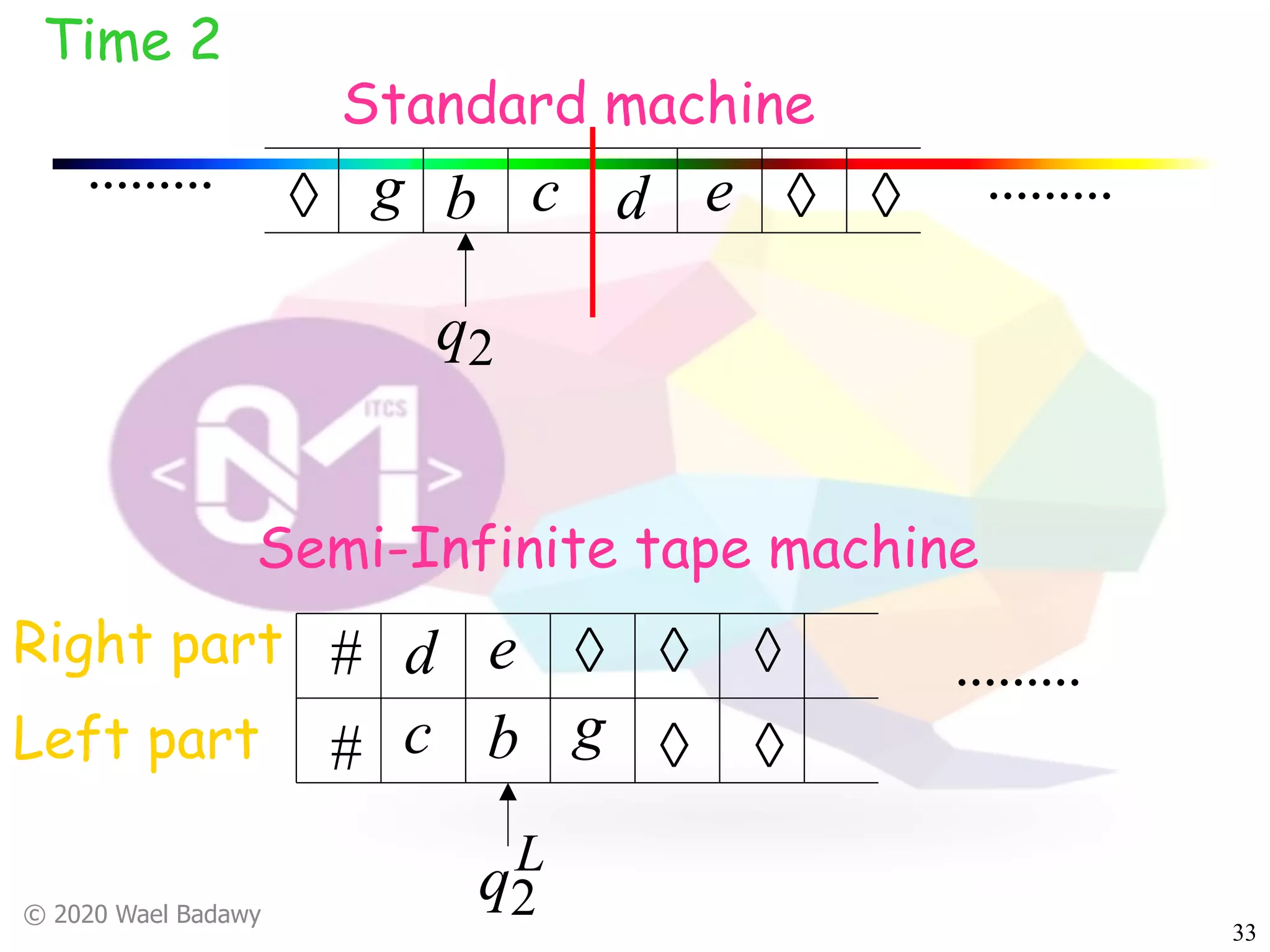
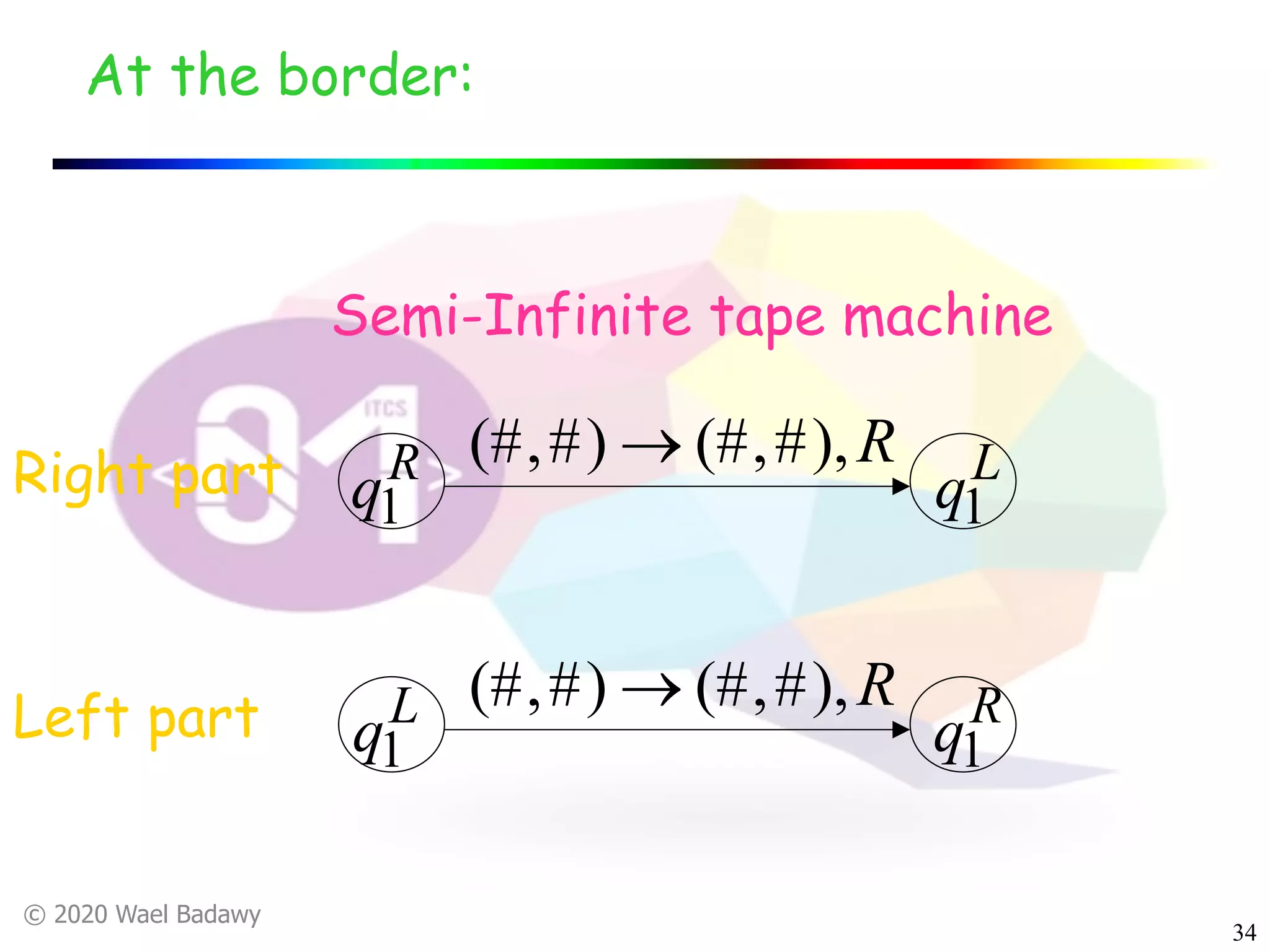
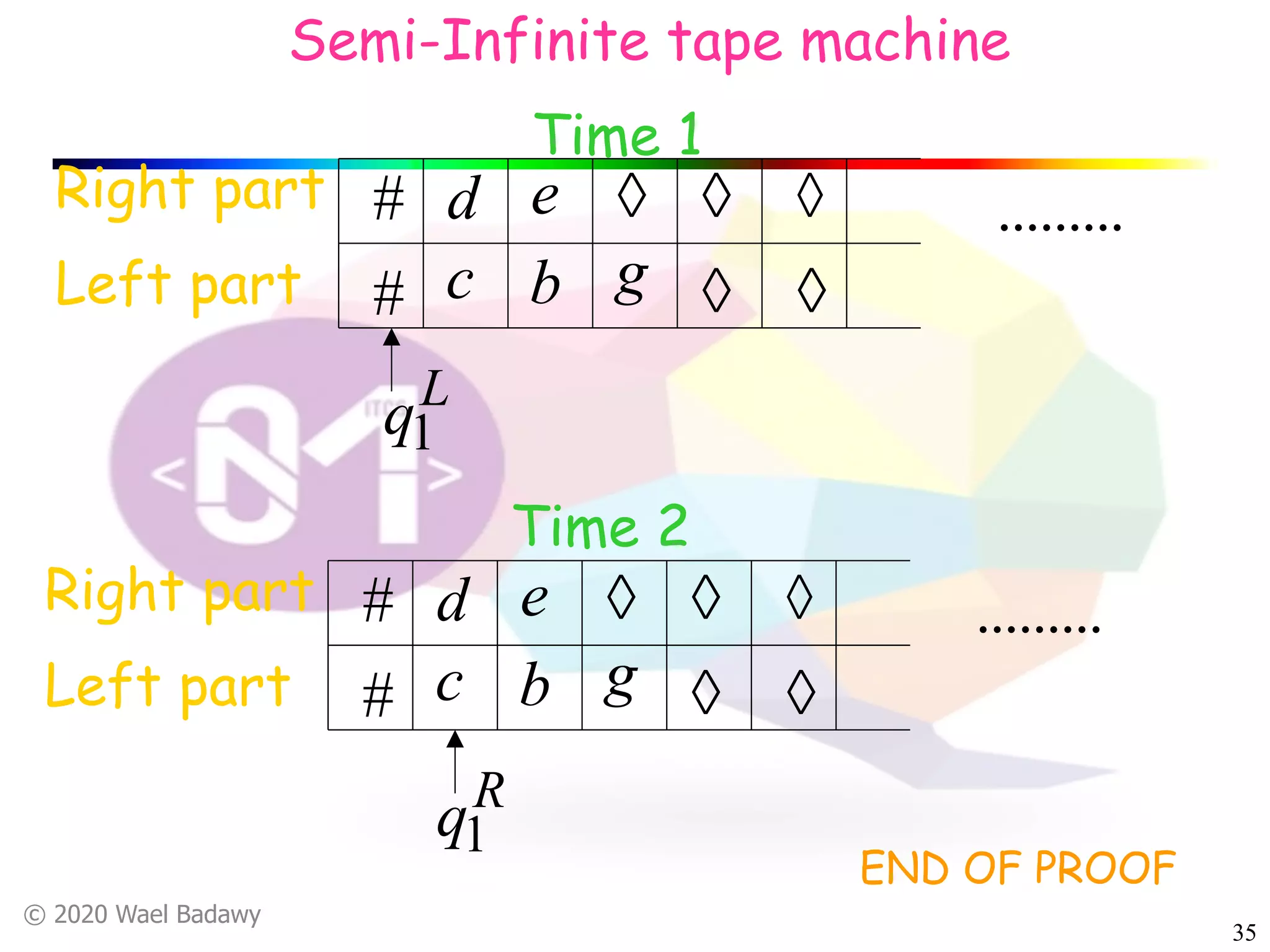
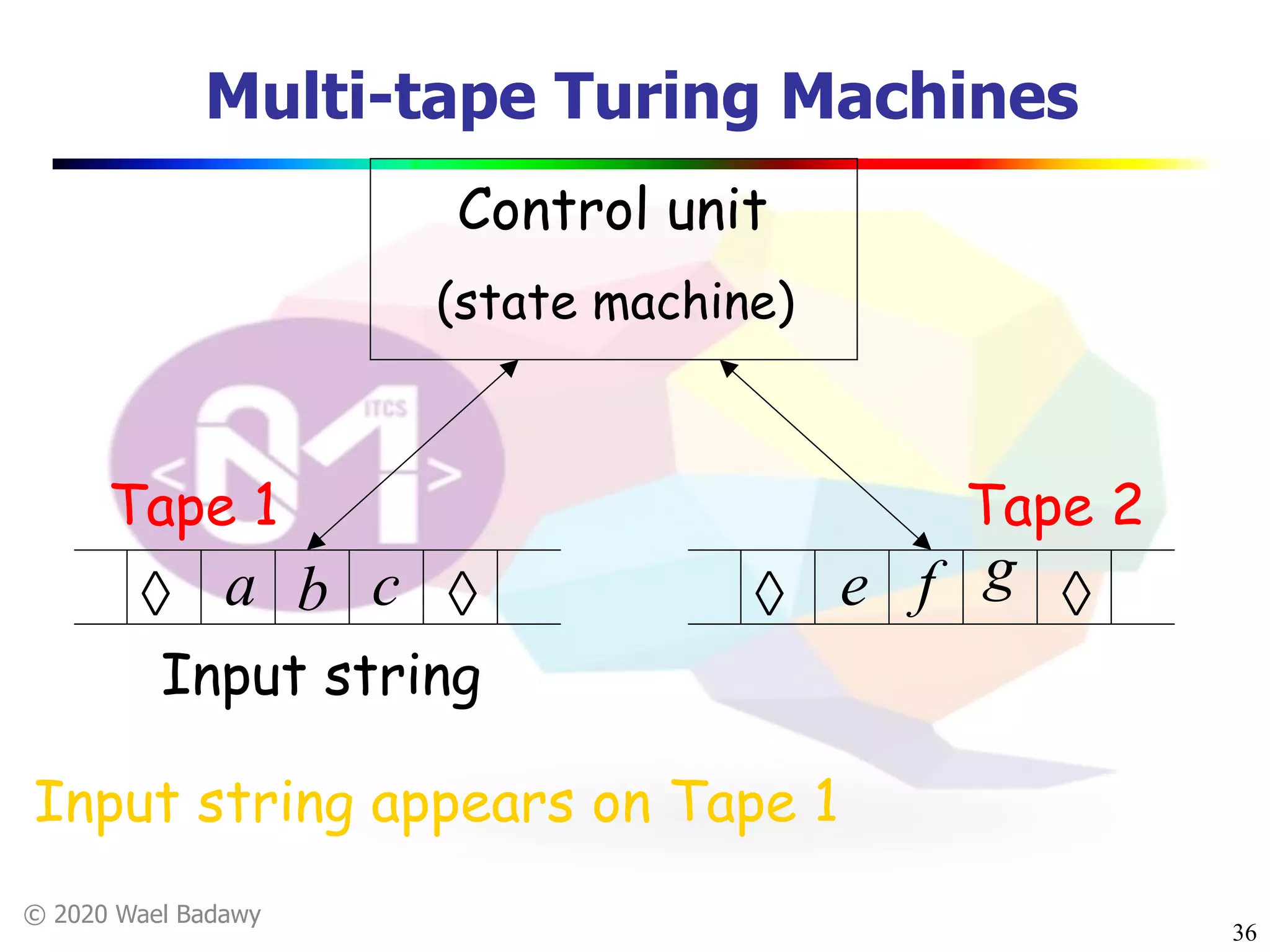
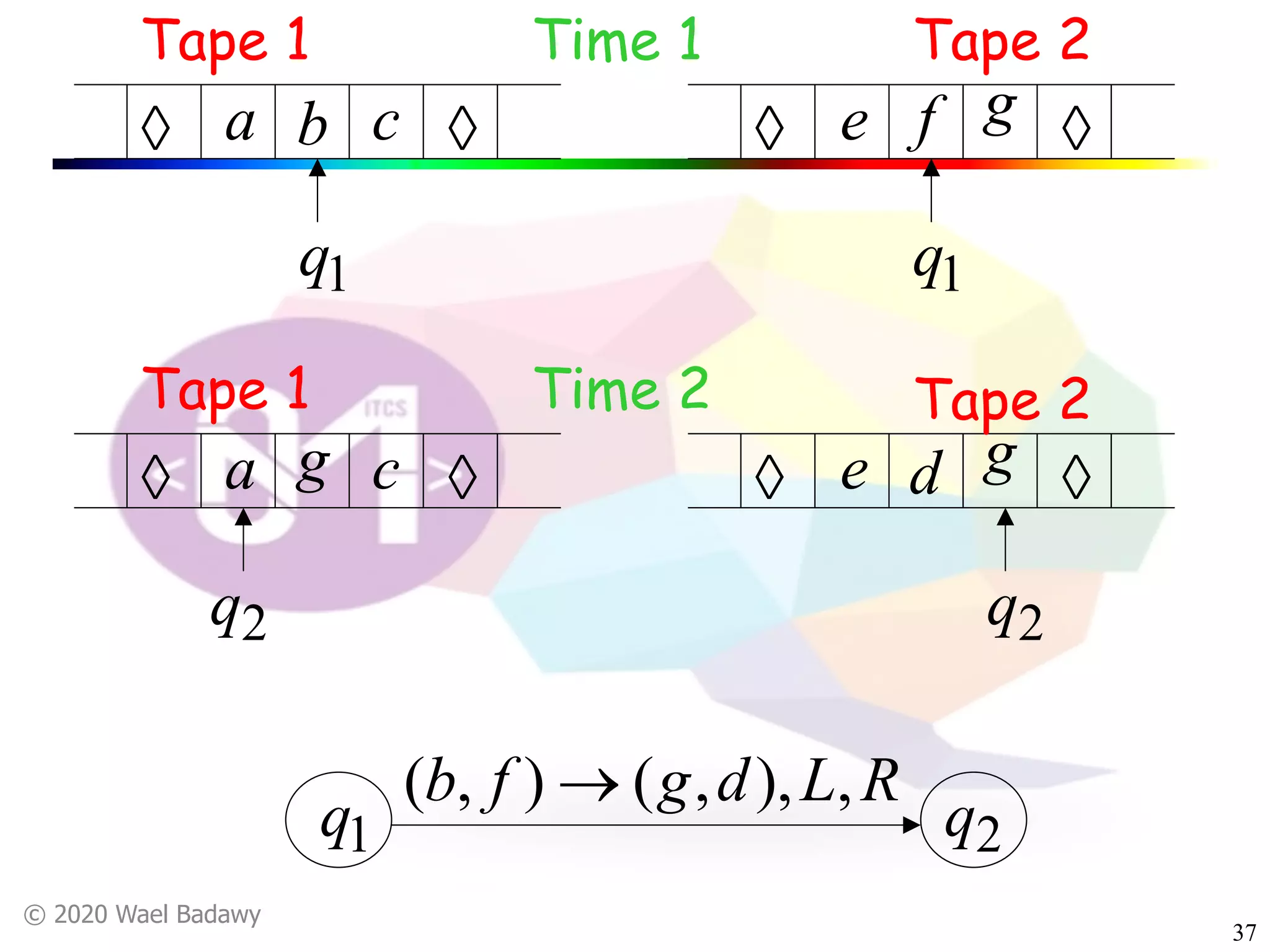
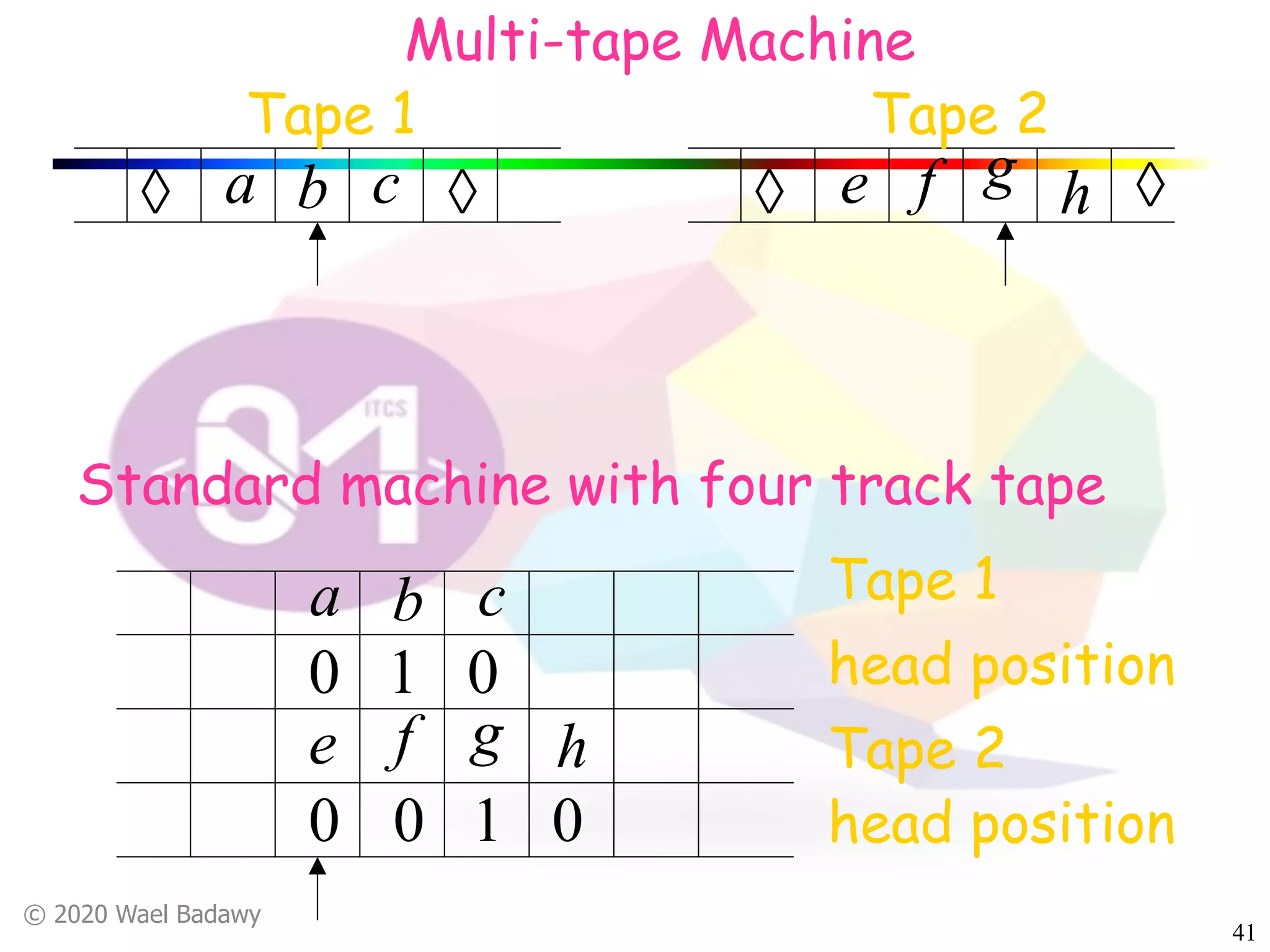
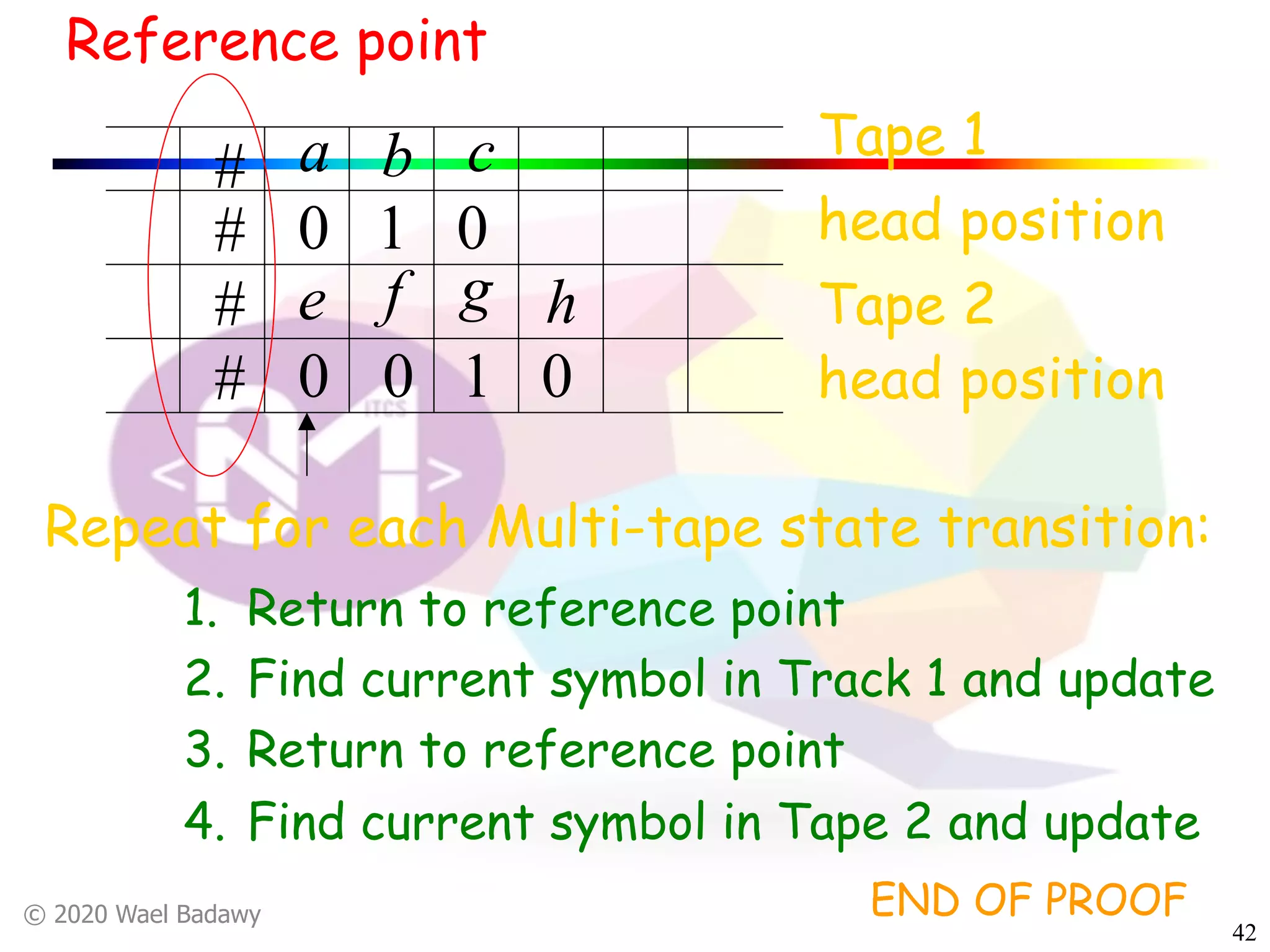
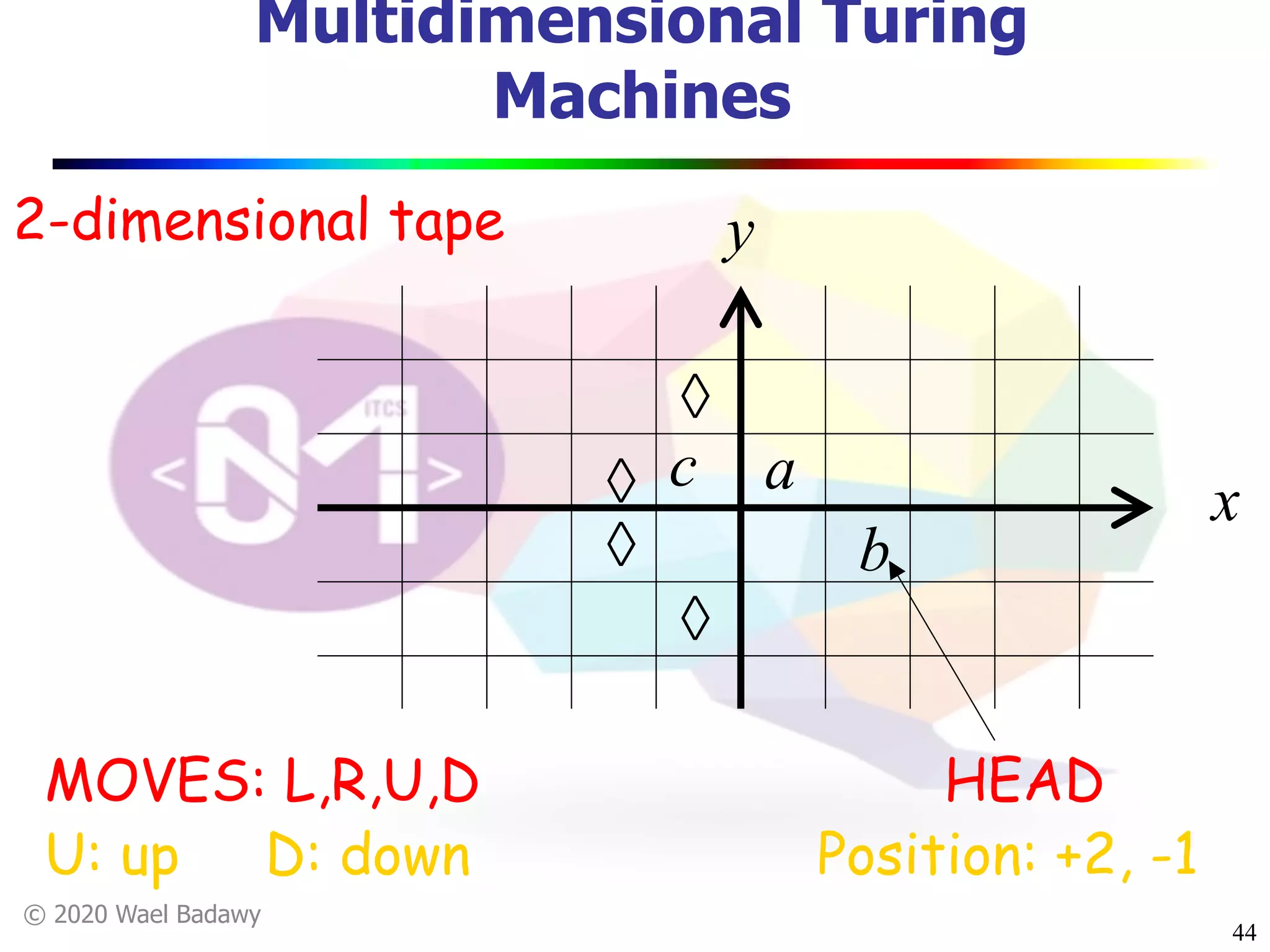
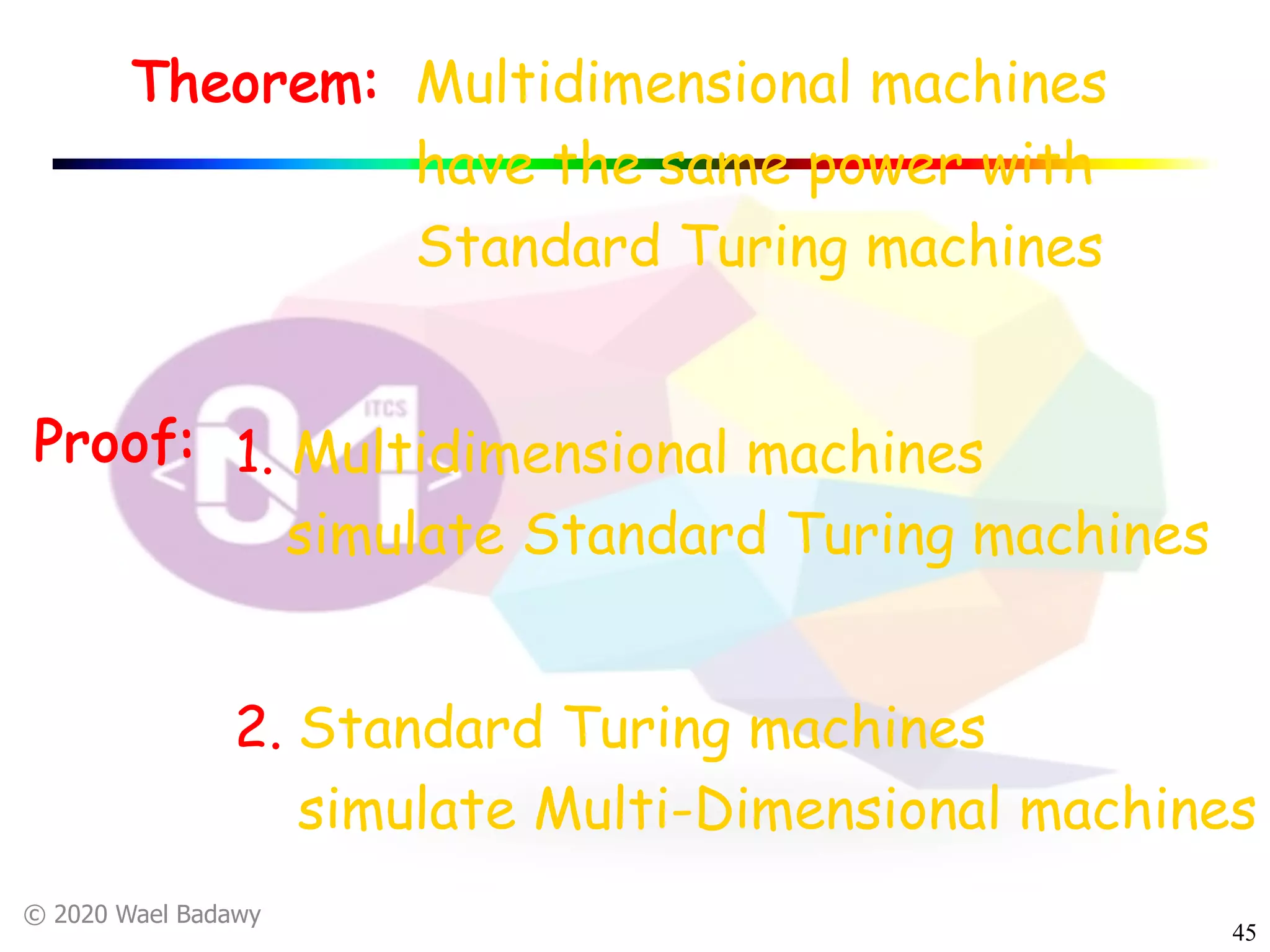
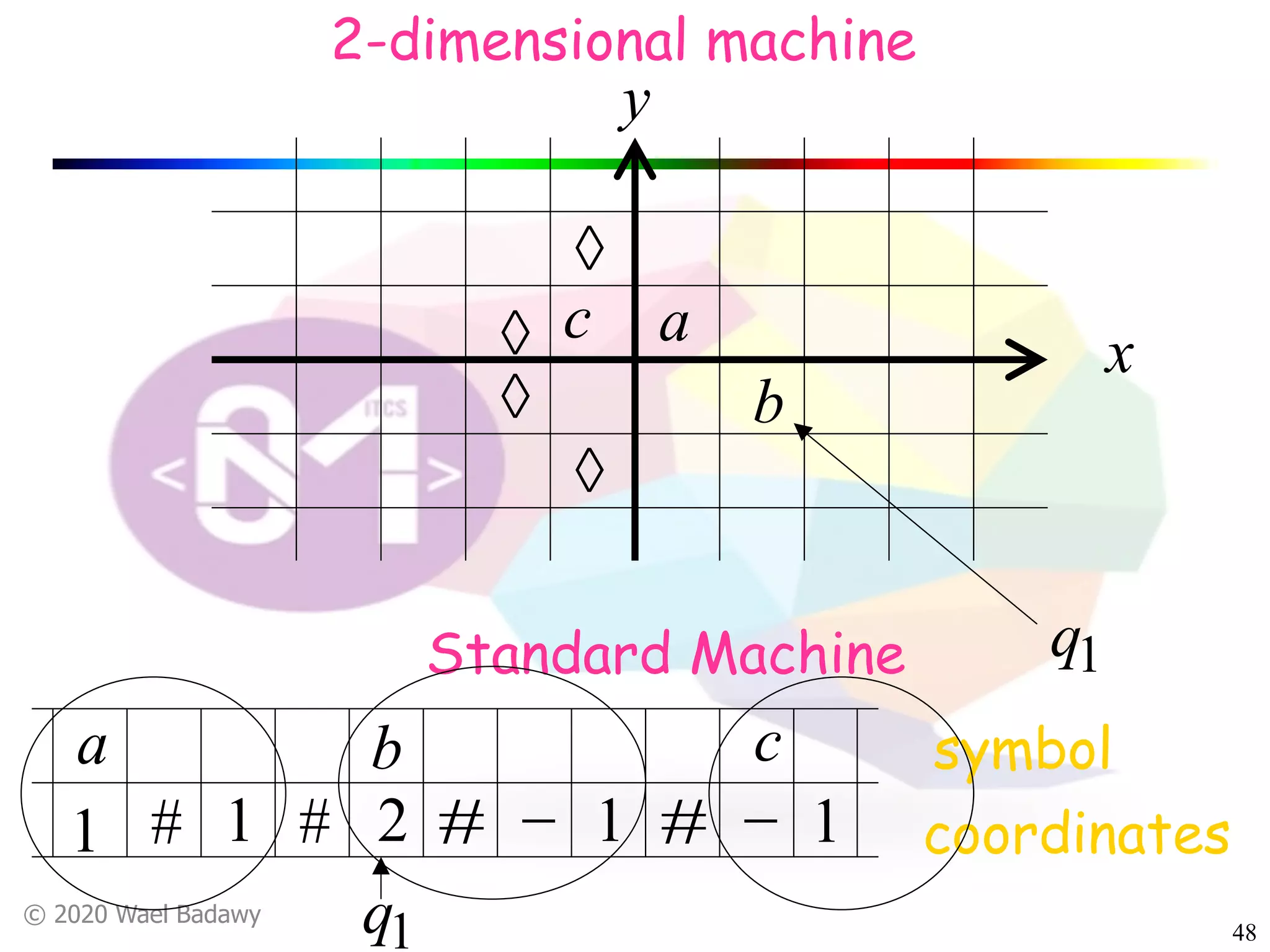
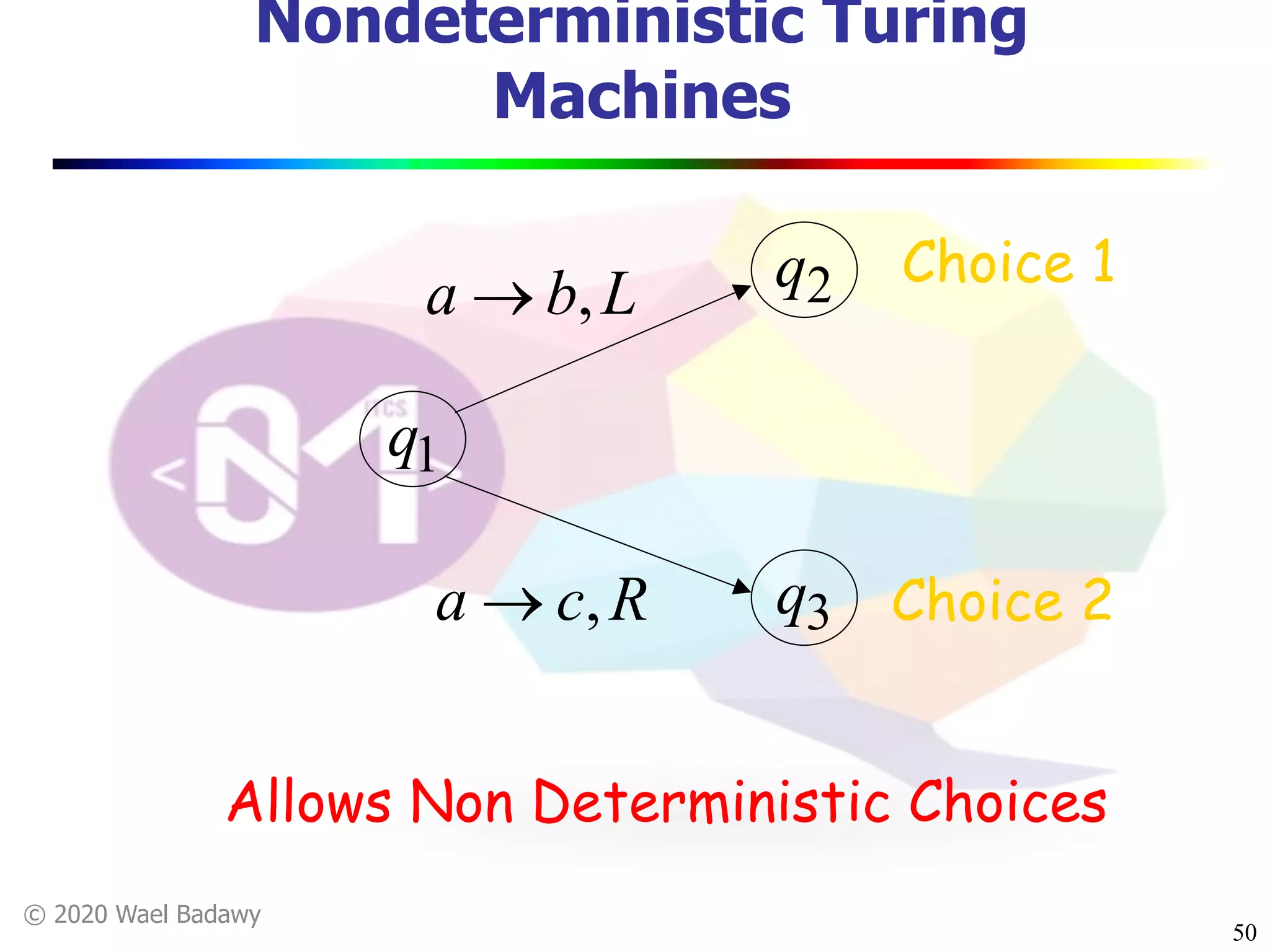
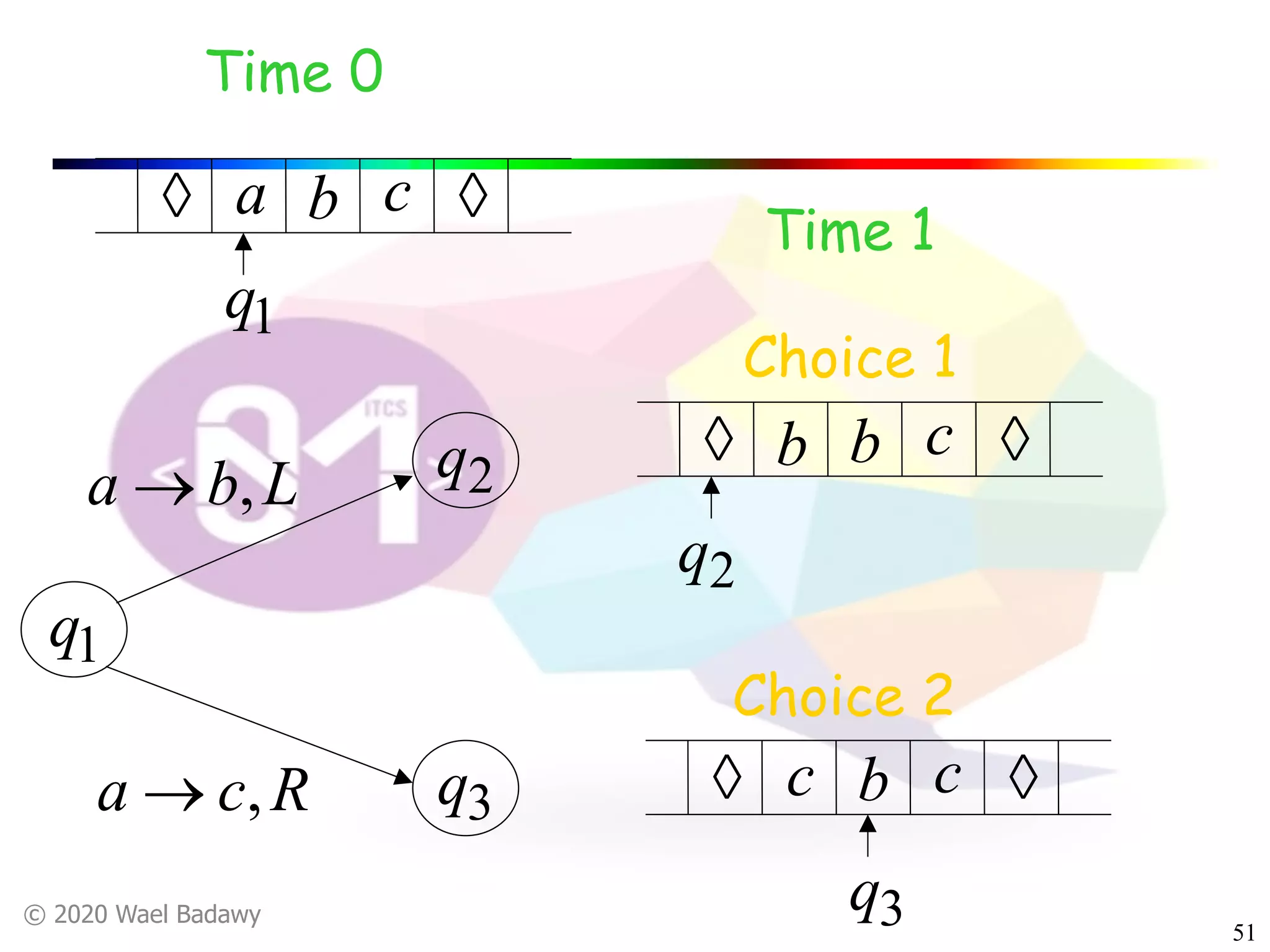
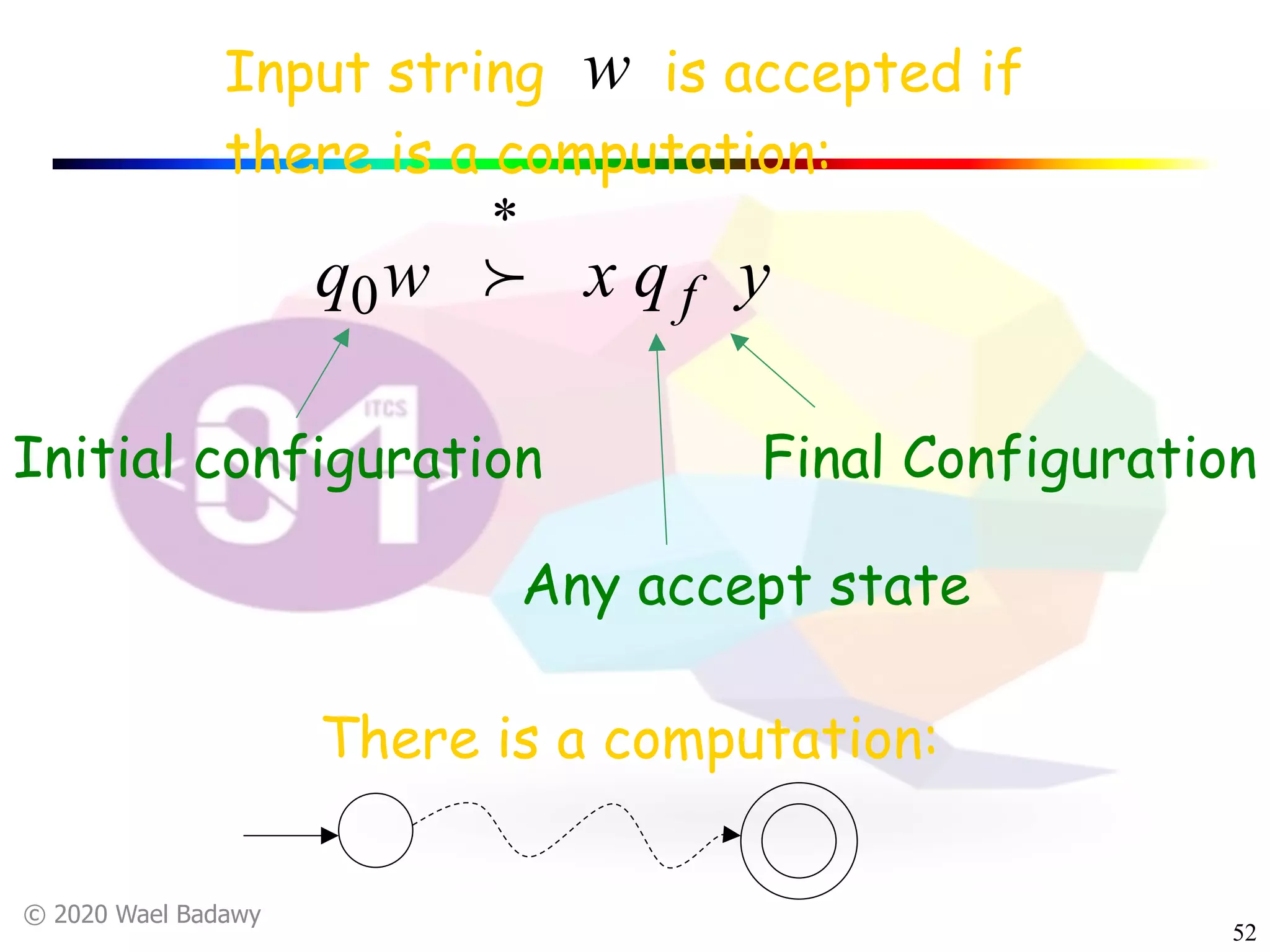
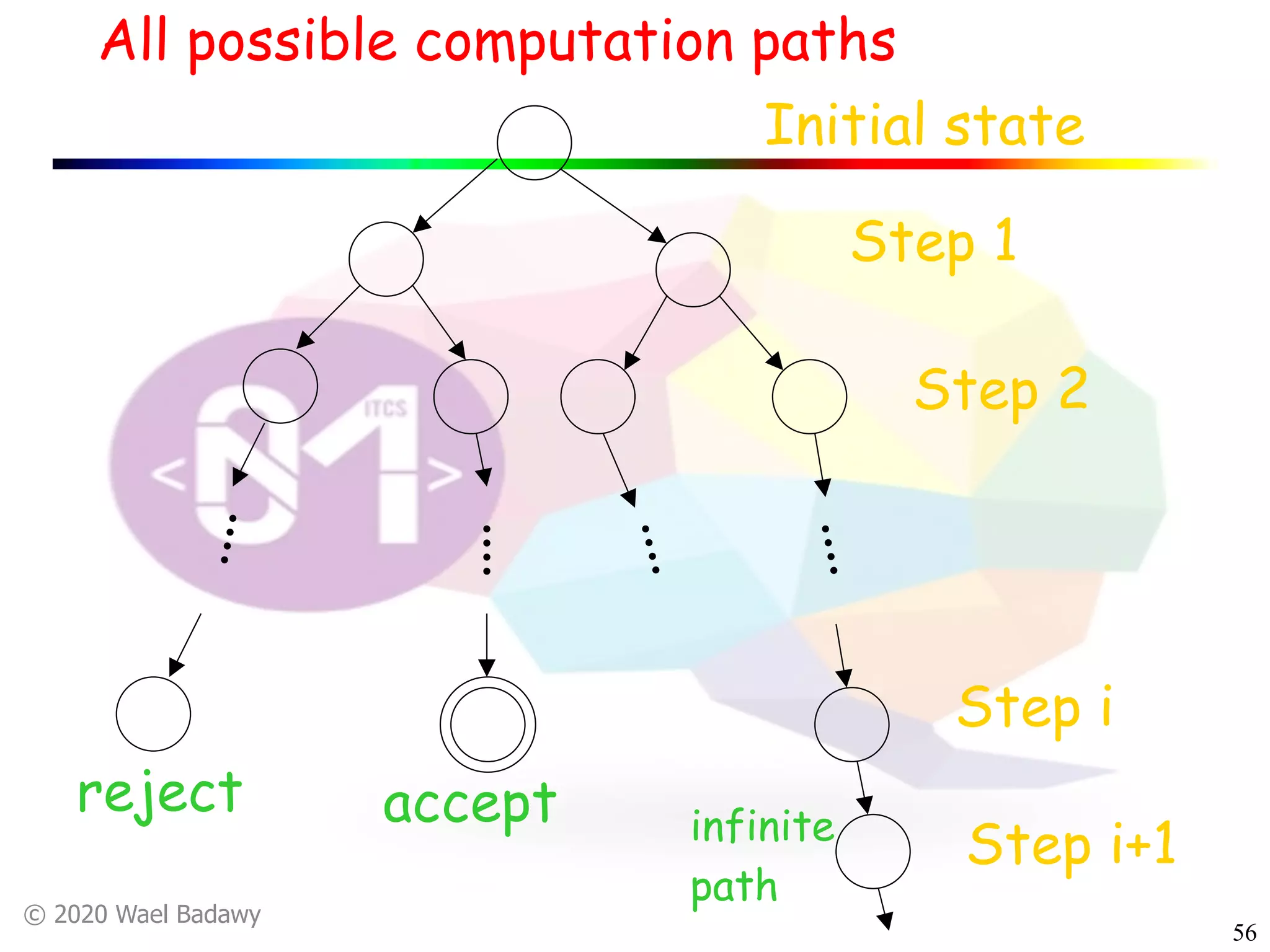
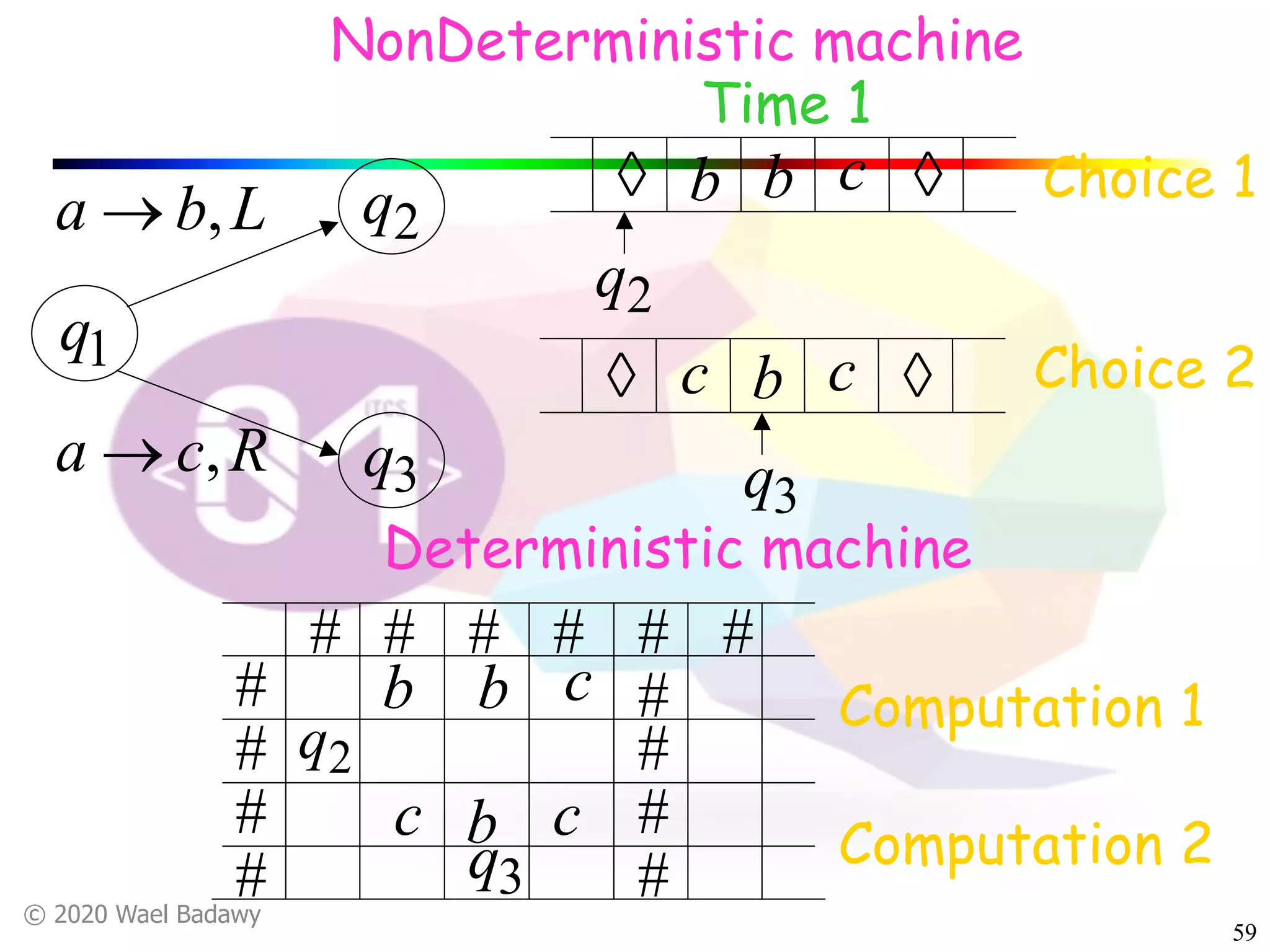
The document discusses variations of Turing machines and proves they have the same computational power as standard Turing machines. It introduces Turing machines with additional capabilities like staying in place, semi-infinite tapes, multiple tapes, and multiple dimensions. It then proves that each variation can simulate a standard Turing machine and vice versa through techniques like tracking multiple tape positions or dimensions on a single tape. This establishes that all the machine variations accept the same formal languages.

1. © 2020 Wael Badawy
1
Turing’s Thesis
1
DISCLAIMER:
This video is optimized for HD large display using
patented and patent-pending “Nile Codec”, the first
Egyptian Video Codec for more information,
PLEASE check https://NileCodec.com
Also available as a PodCast

2. © 2020 Wael Badawy
Copyright © 2020 Wael Badawy. All rights reserved
n This video is subject to copyright owned by Wael Badawy “WB”. Any
reproduction or republication of all or part of this video is expressly prohibited
unless WB has explicitly granted its prior written consent. All other rights
reserved.
n This video is intended for education and information only and is offered AS IS,
without any warranty of the accuracy or the quality of the content. Any other
use is strictly prohibited. The viewer is fully responsible to verify the accuracy
of the contents received without any claims of costs or liability arising .
n The names, trademarks service marked as logos of WB or the sponsors
appearing in this video may not be used in any any product or service,
without prior express written permission from WB and the video sponsors
n Neither WB nor any party involved in creating, producing or delivering
information and material via this video shall be liable for any direction,
incidental, consequential, indirect of punitive damages arising out of access
to, use or inability to use this content or any errors or omissions in the
content thereof.
n If you will continue to watch this video, you agree to the terms above and
other terms that may be available on http://nu.edu.eg & https://caiwave.net
2

3. © 2020 Wael Badawy

4. © 2020 Wael Badawy
4
Turing’s thesis (1930):
Any computation carried out
by mechanical means
can be performed by a Turing Machine

5. © 2020 Wael Badawy
5
Algorithm:
An algorithm for a problem is a
Turing Machine which solves the problem
The algorithm describes the steps of
the mechanical means
This is easily translated to computation steps
of a Turing machine

6. © 2020 Wael Badawy
6
When we say: There exists an algorithm
We mean: There exists a Turing Machine
that executes the algorithm

7. 7
Variations
of the
Turing Machine
7

8. © 2020 Wael Badawy
8
Read-Write Head
Control Unit
àà a a c àà àb a cb b a a
Deterministic
The Standard Model
Infinite Tape
(Left or Right)

9. © 2020 Wael Badawy
Variations of the Standard
Model
9
• Stay-Option
• Semi-Infinite Tape
• Multitape
• Multidimensional
• Nondeterministic
Turing machines with:
Different Turing Machine Classes

10. © 2020 Wael Badawy
10
We will prove:
each new class has the same power
with Standard Turing Machine
Same Power of two machine classes:
both classes accept the
same set of languages
(accept Turing-Recognizable Languages)

11. © 2020 Wael Badawy
11
Same Power of two classes means:
for any machine of first class1M
there is a machine of second class2M
such that: )()( 21 MLML =
and vice-versa

12. © 2020 Wael Badawy
12
A technique to prove same power.Simulation:
Simulate the machine of one class
with a machine of the other class
First Class
Original Machine
1M 1M
2M
Second Class
Simulation Machine
simulates 1M

13. © 2020 Wael Badawy
13
Configurations in the Original Machine
have corresponding configurations
in the Simulation Machine
nddd !"!! 10Original Machine:
Simulation Machine: nddd ¢¢¢
***
!"!! 10
1M
2M
1M
2M

14. © 2020 Wael Badawy
14
the Simulation Machine
and the Original Machine
accept the same strings
fdOriginal Machine:
Simulation Machine:
fd¢
Accepting Configuration
)()( 21 MLML =

15. © 2020 Wael Badawy
Turing Machines with Stay-
Option
15
The head can stay in the same position
àà a a c àà àb a cb b a a
Left, Right, Stay
L,R,S: possible head moves

16. © 2020 Wael Badawy
16
Example:
àà a a c àà àb a cb b a a
Time 1
àà b a c àà àb a cb b a a
Time 2
1q 2q
1q
2q
Sba ,®

17. © 2020 Wael Badawy
17
Stay-Option machines
have the same power with
Standard Turing machines
Theorem:
Proof: 1. Stay-Option Machines
simulate Standard Turing machines
2. Standard Turing machines
simulate Stay-Option machines

18. © 2020 Wael Badawy
18
1. Stay-Option Machines
simulate Standard Turing machines
Trivial: any standard Turing machine
is also a Stay-Option machine

19. © 2020 Wael Badawy
19
2. Standard Turing machines
simulate Stay-Option machines
We need to simulate the stay head option
with two head moves, one left and one right

20. © 2020 Wael Badawy
20
1q 2q
Sba ,®
1q
Lba ,®
2q
Rxx ,®
Stay-Option Machine
Simulation in Standard Machine
For every possible tape symbol x

21. © 2020 Wael Badawy
21
1q 2q
Lba ,®
1q 2q
Lba ,®
Stay-Option Machine
Simulation in Standard Machine
Similar for Right moves
For other transitions nothing changes

22. © 2020 Wael Badawy
22
example of simulation
à àa a b a
1q
Stay-Option Machine:
1
à àb a b a
2q
2
1q 2qSba ,®
Simulation in Standard Machine:
à àa a b a
1q
1
à àb a b a
2q
2
à àb a b a
3q
3
END OF PROOF

23. © 2020 Wael Badawy
23
A useful trick: Multiple Track Tape
à
à
à
à
à
à
b
d
a
b
b
a
a
c
track 1
track 2
One symbol ),( ba
One head
helps for more complicated simulations
One Tape
It is a standard Turing machine, but each tape alphabet symbol
describes a pair of actual useful symbols

24. © 2020 Wael Badawy
24
à
à
à
à
à
à
b
d
a
b
b
a
a
c
track 1
track 2
1q 2q
Ldcab ),,(),( ®
1q
à
à
à
à
à
à
b
d
a
b
c
d
a
c
track 1
track 2
2q

25. © 2020 Wael Badawy
Semi-Infinite Tape
25
.........a b a c à à
• When the head moves left from the border,
it returns back to leftmost position
The head extends infinitely only to the right
• Initial position is the leftmost cell

26. © 2020 Wael Badawy
26
Semi-Infinite machines
have the same power with
Standard Turing machines
Theorem:
Proof:
2. Semi-Infinite Machines
simulate Standard Turing machines
1. Standard Turing machines
simulate Semi-Infinite machines

27. © 2020 Wael Badawy
27
1. Standard Turing machines simulate
Semi-Infinite machines:
a. insert special symbol
at left of input string
#
a b a c à à#
b. Add a self-loop
to every state
(except states with no
outgoing transitions)
R,##®
Standard Turing Machine
àà
Semi-Infinite machine modifications
..................

28. © 2020 Wael Badawy
28
2. Semi-Infinite tape machines simulate
Standard Turing machines:
Standard machine
.........
Semi-Infinite tape machine
..................
Squeeze infinity of both directions
to one direction

29. © 2020 Wael Badawy
29
Standard machine
.........
Semi-Infinite tape machine with two tracks
..................
reference point
#
#
Right part
Left part
à à àa b c d e
ac b
d e à à
à
à
à

30. © 2020 Wael Badawy
30
1q
2q
R
q2
L
q1
L
q2 R
q1
Left part Right part
Standard machine
Semi-Infinite tape machine

31. © 2020 Wael Badawy
31
1q 2q
Rga ,®
Standard machine
L
q1
L
q2
Lgxax ),,(),( ®
R
q1
R
q2
Rxgxa ),,(),( ®
Semi-Infinite tape machine
Left part
Right part
For all tape symbols x

32. © 2020 Wael Badawy
32
Standard machine
..................
à à àa b c d e
1q
.........
Semi-Infinite tape machine
#
#
Right part
Left part ac b
d e à à
à
à
à
L
q1
Time 1

33. © 2020 Wael Badawy
33
Time 2
à à àg b c d e
2q
#
#
Right part
Left part gc b
d e à à
à
à
à
L
q2
Standard machine
..................
.........
Semi-Infinite tape machine

34. © 2020 Wael Badawy
34
L
q1
R
q1
R),#,(#)#,(# ®
Semi-Infinite tape machine
Left part
At the border:
R
q1
L
q1
R),#,(#)#,(# ®Right part

35. © 2020 Wael Badawy
35
.........
Semi-Infinite tape machine
#
#
Right part
Left part gc b
d e à à
à
à
à
L
q1
.........#
#
Right part
Left part gc b
d e à à
à
à
à
R
q1
Time 1
Time 2
END OF PROOF

36. © 2020 Wael Badawy
Multi-tape Turing Machines
36
àà a b c àà e f g
Control unit
Tape 1 Tape 2
Input string
Input string appears on Tape 1
(state machine)

37. © 2020 Wael Badawy
37
àà a b c àà e f g
1q 1q
àà a g c àà e d g
2q 2q
Time 1
Time 2
RLdgfb ,),,(),( ®
1q 2q
Tape 1 Tape 2
Tape 1 Tape 2

38. © 2020 Wael Badawy
38
Multi-tape machines
have the same power with
Standard Turing machines
Theorem:
Proof: 1. Multi-tape machines
simulate Standard Turing machines
2. Standard Turing machines
simulate Multi-tape machines

39. © 2020 Wael Badawy
39
1. Multi-tape machines simulate
Standard Turing Machines:
Trivial: Use one tape

40. © 2020 Wael Badawy
40
2. Standard Turing machines simulate
Multi-tape machines:
• Uses a multi-track tape to simulate
the multiple tapes
• A tape of the Multi-tape machine
corresponds to a pair of tracks
Standard machine:

41. © 2020 Wael Badawy
41
àà a b c hà e f g à
Multi-tape Machine
Tape 1 Tape 2
Standard machine with four track tape
a b c
e f g
0 0
0 0
1
1
Tape 1
head position
Tape 2
head position
h
0

42. © 2020 Wael Badawy
42
Repeat for each Multi-tape state transition:
1. Return to reference point
2. Find current symbol in Track 1 and update
3. Return to reference point
4. Find current symbol in Tape 2 and update
a b c
e f g
0 0
0 0
1
1
Tape 1
head position
Tape 2
head position
h
0
#
#
#
#
Reference point
END OF PROOF

43. © 2020 Wael Badawy
43
( steps)
}{ nn
baL =
Standard Turing machine:
Go back and forth times)( 2
nO
2-tape machine:
1. Copy to tape 2n
b
2. Compare on tape 1
and on tape 2
)(nO
n
b
n
a
to match the a’s with the b’s
( steps))(nO
)( 2
nO time
)(nO time
Same power doesn’t imply same speed:

44. © 2020 Wael Badawy
Multidimensional Turing
Machines
44
x
y
a
b
c
2-dimensional tape
HEAD
Position: +2, -1
MOVES: L,R,U,D
U: up D: down
à
à
à
à

45. © 2020 Wael Badawy
45
Multidimensional machines
have the same power with
Standard Turing machines
Theorem:
Proof: 1. Multidimensional machines
simulate Standard Turing machines
2. Standard Turing machines
simulate Multi-Dimensional machines

46. © 2020 Wael Badawy
46
1. Multidimensional machines simulate
Standard Turing machines
Trivial: Use one dimension

47. © 2020 Wael Badawy
47
2. Standard Turing machines simulate
Multidimensional machines
Standard machine:
• Use a two track tape
• Store symbols in track 1
• Store coordinates in track 2

48. © 2020 Wael Badawy
48
x
y
a
b
cà
à
à
à
a
1
b
#
symbol
coordinates
2-dimensional machine
Standard Machine
1 # 2 # 1-
c
# -
1q
1q
1

49. © 2020 Wael Badawy
49
Repeat for each transition followed
in the 2-dimensional machine:
1. Update current symbol
2. Compute coordinates of next position
3. Find next position on tape
Standard machine:
END OF PROOF

50. © 2020 Wael Badawy
Nondeterministic Turing
Machines
50
Lba ,®
Rca ,®
1q
2q
3q
Allows Non Deterministic Choices
Choice 1
Choice 2

51. © 2020 Wael Badawy
51
a b cà à
1q
Lba ,®
Rca ,®
1q
2q
3q
Time 0
Time 1
b b cà à
2q
c b cà à
3q
Choice 1
Choice 2

52. © 2020 Wael Badawy
52
Input string is accepted if
there is a computation:
w
yqxwq f
*
!0
Initial configuration Final Configuration
Any accept state
There is a computation:

53. © 2020 Wael Badawy
53
Nondeterministic machines
have the same power with
Standard Turing machines
Theorem:
Proof: 1. Nondeterministic machines
simulate Standard Turing machines
2. Standard Turing machines
simulate Nondeterministic machines

54. © 2020 Wael Badawy
54
1. Nondeterministic Machines simulate
Standard (deterministic) Turing Machines
Trivial: every deterministic machine
is also nondeterministic

55. © 2020 Wael Badawy
55
2. Standard (deterministic) Turing machines
simulate Nondeterministic machines:
• Stores all possible computations
of the non-deterministic machine
on the 2-dimensional tape
Deterministic machine:
• Uses a 2-dimensional tape
(equivalent to standard Turing machine with one tape)

56. © 2020 Wael Badawy
56
All possible computation paths
Initial state
Step 1
Step 2
Step i
Step i+1
acceptreject
infinite
path

57. © 2020 Wael Badawy
57
The Deterministic Turing machine
simulates all possible computation paths:
•with breadth-first search
•simultaneously
•step-by-step
depth-first may result getting stuck at exploring
an infinite path before discovering the accepting path

58. © 2020 Wael Badawy
58
a b cà à
1q
Lba ,®
Rca ,®
1q
2q
3q
Time 0
NonDeterministic machine
Deterministic machine
a b c
1q
# # # # ##
#
#
# # #
#
#
# #
current
configuration

59. © 2020 Wael Badawy
59
Lba ,®
Rca ,®
1q
2q
3q
b b c
2q
# # # # ##
#
# #
#
# #
Computation 1
b b cà à
2q
Choice 1
c b cà à
3q
Choice 2
c b c
3q ##
Computation 2
NonDeterministic machine
Deterministic machine
Time 1

60. © 2020 Wael Badawy
60
Repeat
For each configuration in current step
of non-deterministic machine,
if there are two or more choices:
1. Replicate configuration
2. Change the state in the replicas
Deterministic Turing machine
Until either the input string is accepted
or rejected in all configurations

61. © 2020 Wael Badawy
61
If the non-deterministic machine accepts
the input string:
The deterministic machine accepts and halts too
The simulation takes in the worst case
exponential time compared to the
shortest length of an accepting path

62. © 2020 Wael Badawy
62
If the non-deterministic machine does not
accept the input string:
1. The simulation halts if all paths
reach a halting state
OR
2. The simulation never terminates
if there is a never-ending path (infinite loop)
In either case the deterministic machine
rejects too (1. by halting or 2. by simulating the infinite loop)
END OF PROOF