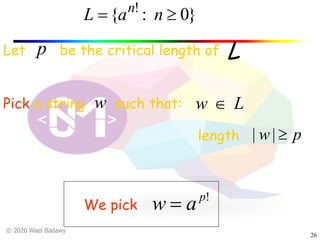
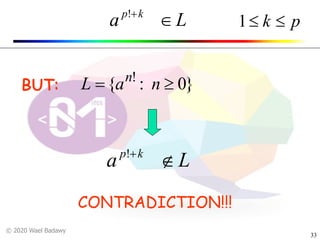
This document presents proofs that three languages are not regular using the pumping lemma. It first proves that the language {a^n b^n | n >= 0} is not regular by picking the string "abba" and showing it cannot be pumped. It then proves that the language {w | the number of a's is not equal to the number of b's} is not regular, again by picking a string and showing it cannot be pumped. Finally, it proves that the language of strings with an equal number of 1's and 0's is not regular using a similar pumping argument.

1. © 2020 Wael Badawy
1
More Applications of the Pumping Lemma
1
DISCLAIMER:
This video is optimized for HD large display using
patented and patent-pending “Nile Codec”, the first
Egyptian Video Codec for more information,
PLEASE check https://NileCodec.com
Also available as a PodCast

2. © 2020 Wael Badawy
Copyright © 2020 Wael Badawy. All rights reserved
n This video is subject to copyright owned by Wael Badawy “WB”. Any
reproduction or republication of all or part of this video is expressly prohibited
unless WB has explicitly granted its prior written consent. All other rights
reserved.
n This video is intended for education and information only and is offered AS IS,
without any warranty of the accuracy or the quality of the content. Any other
use is strictly prohibited. The viewer is fully responsible to verify the accuracy
of the contents received without any claims of costs or liability arising .
n The names, trademarks service marked as logos of WB or the sponsors
appearing in this video may not be used in any any product or service,
without prior express written permission from WB and the video sponsors
n Neither WB nor any party involved in creating, producing or delivering
information and material via this video shall be liable for any direction,
incidental, consequential, indirect of punitive damages arising out of access
to, use or inability to use this content or any errors or omissions in the
content thereof.
n If you will continue to watch this video, you agree to the terms above and
other terms that may be available on http://nu.edu.eg & https://caiwave.net
2

3. © 2020 Wael Badawy

4. © 2020 Wael Badawy
The Pumping Lemma:
4
• Given a infinite regular language L
• there exists an integer (critical length)p
• for any string with lengthLwÎ pw ³||
• we can write zyxw =
• with andpyx £|| 1|| ³y
• such that: Lzyx i
Î ...,2,1,0=i

5. © 2020 Wael Badawy
5
Regular languages
Non-regular languages *}:{ SÎ= vvvL R

6. © 2020 Wael Badawy
6
Theorem: The language
is not regular
Proof: Use the Pumping Lemma
*}:{ SÎ= vvvL R
},{ ba=S

7. © 2020 Wael Badawy
7
Assume for contradiction
that is a regular languageL
Since is infinite
we can apply the Pumping Lemma
L
*}:{ SÎ= vvvL R

8. © 2020 Wael Badawy
8
pppp
abbaw =We pick
Let be the critical length for
Pick a string such that:w Lw Î
pw ³||length
p
and
*}:{ SÎ= vvvL R
L

9. © 2020 Wael Badawy
9
we can write: zyxabbaw pppp
==
with lengths:
From the Pumping Lemma:
ababbabaaaaxyz ..................=
x y z
p p p p
1||,|| ³£ ypyx
pkay k
££= 1,Thus:
=w

10. © 2020 Wael Badawy
10
From the Pumping Lemma: Lzyx i
Î
...,2,1,0=i
Thus: Lzyx Î2
pppp
abbazyx = pkay k
££= 1,

11. © 2020 Wael Badawy
11
From the Pumping Lemma:
Lababbabaaaaaazxy ∈.....................=2
x y z
kp + p p p
y
Lzyx Î2
Thus: Labba pppkp
Î+
pppp
abbazyx = pkay k
££= 1,

12. © 2020 Wael Badawy
12
Labba pppkp
Ï+
BUT:
CONTRADICTION!!!
1³k
*}:{ SÎ= vvvL R
Labba pppkp
Î+

13. © 2020 Wael Badawy
13
Our assumption that
is a regular language is not true
L
Conclusion: L is not a regular language
Therefore:
END OF PROOF

14. © 2020 Wael Badawy
14
Regular languages
Non-regular languages
}0,:{ ³= +
lncbaL lnln

15. © 2020 Wael Badawy
15
Theorem: The language
is not regular
Proof: Use the Pumping Lemma
}0,:{ ³= +
lncbaL lnln

16. © 2020 Wael Badawy
16
Assume for contradiction
that is a regular languageL
Since is infinite
we can apply the Pumping Lemma
L
}0,:{ ³= +
lncbaL lnln

17. © 2020 Wael Badawy
17
ppp
cbaw 2
=We pick
Let be the critical length of
Pick a string such that:w Lw Î
pw ³||length
p
}0,:{ ³= +
lncbaL lnln
and
L

18. © 2020 Wael Badawy
18
We can write zyxcbaw ppp
== 2
With lengths
From the Pumping Lemma:
cccbcabaaaaaxyz ..................=
x y z
p p p2
1||,|| ³£ ypyx
Thus:
=w
pkay k
££= 1,

19. © 2020 Wael Badawy
19
From the Pumping Lemma: Lzyx i
Î
...,2,1,0=i
Thus:
ppp
cbazyx 2
=
Lxzzyx ∈=0
pkay k
££= 1,

20. © 2020 Wael Badawy
20
From the Pumping Lemma:
Lcccbcabaaaxz Î= ...............
x z
kp - p p2
Lxz Î
Thus: Lcba ppkp
Î- 2
ppp
cbazyx 2
= pkay k
££= 1,

21. © 2020 Wael Badawy
21
Lcba ppkp
Ï- 2
BUT:
CONTRADICTION!!!
}0,:{ ³= +
lncbaL lnln
1³kLcba ppkp
Î- 2

22. © 2020 Wael Badawy
22
Our assumption that
is a regular language is not true
L
Conclusion: L is not a regular language
Therefore:
END OF PROOF

23. © 2020 Wael Badawy
23
Regular languages
Non-regular languages }0:{ !
³= naL n

24. © 2020 Wael Badawy
24
Theorem: The language
is not regular
Proof: Use the Pumping Lemma
}0:{ !
³= naL n
nnn ×-×= )1(21! !

25. © 2020 Wael Badawy
25
Assume for contradiction
that is a regular languageL
Since is infinite
we can apply the Pumping Lemma
L
}0:{ !
³= naL n

26. © 2020 Wael Badawy
26
!p
aw =We pick
Let be the critical length of
Pick a string such that:w Lw Î
pw ³||length
p
}0:{ !
³= naL n
L

27. © 2020 Wael Badawy
27
We can write zyxaw p
== !
With lengths
From the Pumping Lemma:
aaaaaaaaaaaxyz p
...............!
==
x y z
p pp -!
1||,|| ³£ ypyx
pkay k
££= 1,Thus:
=w

28. © 2020 Wael Badawy
28
From the Pumping Lemma: Lzyx i
Î
...,2,1,0=i
Thus:
!p
azyx =
Lzyx Î2
pkay k
££= 1,

29. © 2020 Wael Badawy
29
From the Pumping Lemma:
Laaaaaaaaaaaazxy Î= ..................2
x y z
kp + pp -!
Thus:
!p
azyx = pkay k
££= 1,
Lzyx Î2
y
La kp
Î+!

30. © 2020 Wael Badawy
30
La kp
Î+!
!! zkp =+
}0:{ !
³= naL nSince:
pk ££1
There must exist such that:z

31. © 2020 Wael Badawy
31
However:
)!1(
)1(!
!!
!!
!
+=
+=
+<
+£
+£
p
pp
ppp
pp
ppkp +! for 1>p
)!1(! +<+ pkp
!! zkp ¹+ for any z

32. © 2020 Wael Badawy
32
for 1=p
we could pick string
!p
aw ¢
=
where pp >¢
and we would obtain the same conclusion:
!! zkp ¹+¢ for any z

33. © 2020 Wael Badawy
33
La kp
Î+!
La kp
Ï+!
BUT:
CONTRADICTION!!!
}0:{ !
³= naL n
pk ££1

34. © 2020 Wael Badawy
34
Our assumption that
is a regular language is not true
L
Conclusion: L is not a regular language
Therefore:
END OF PROOF