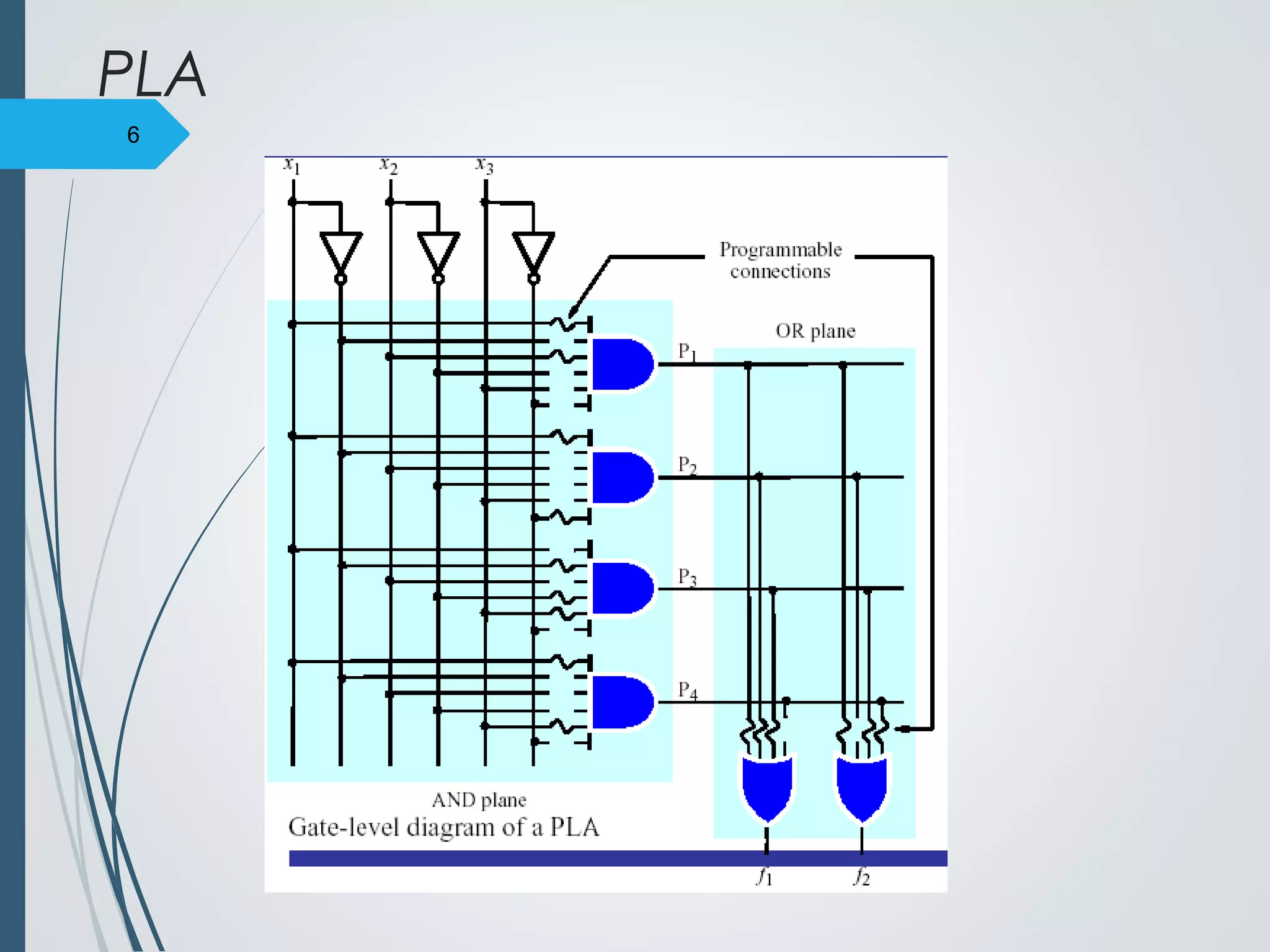
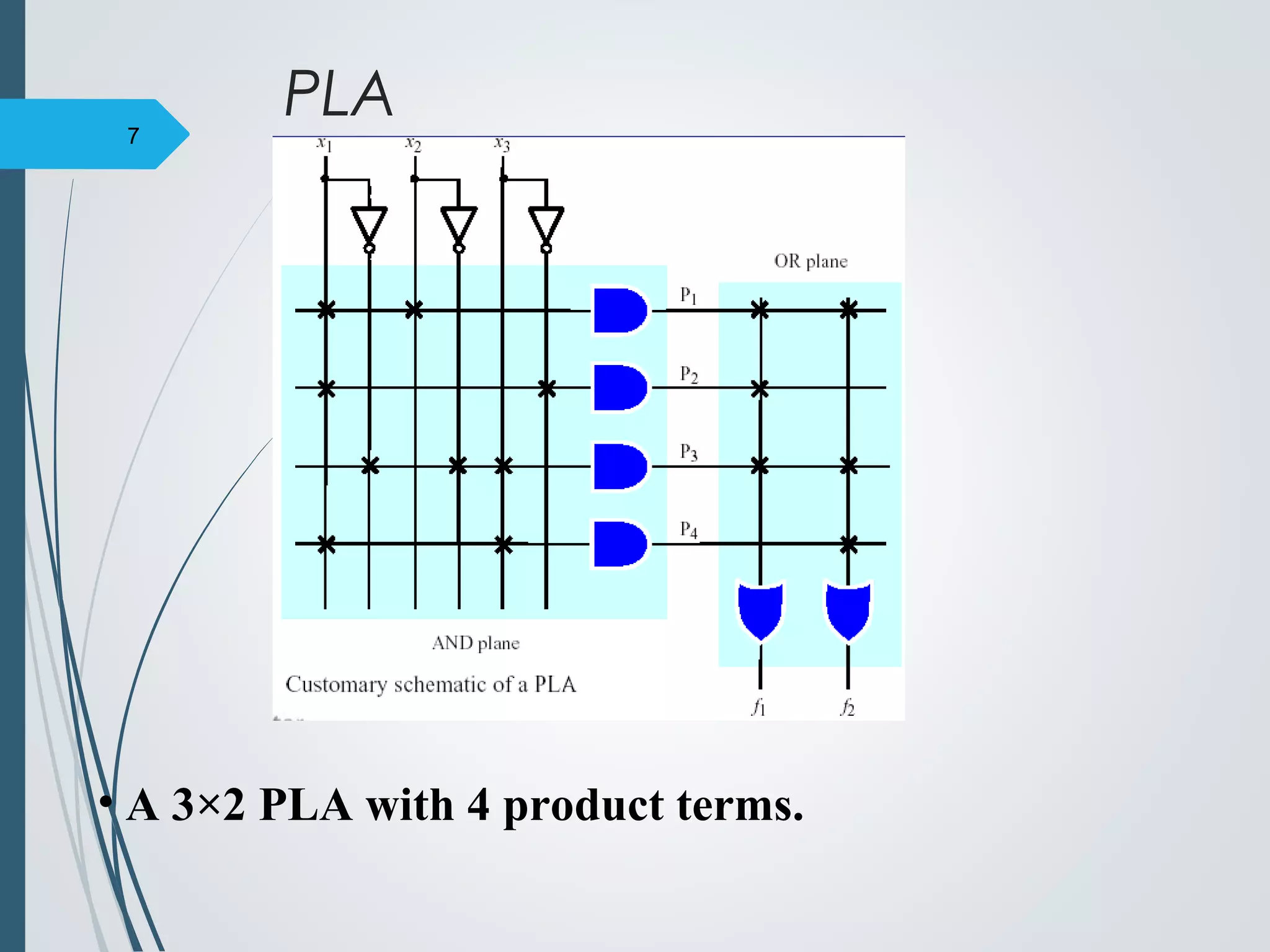
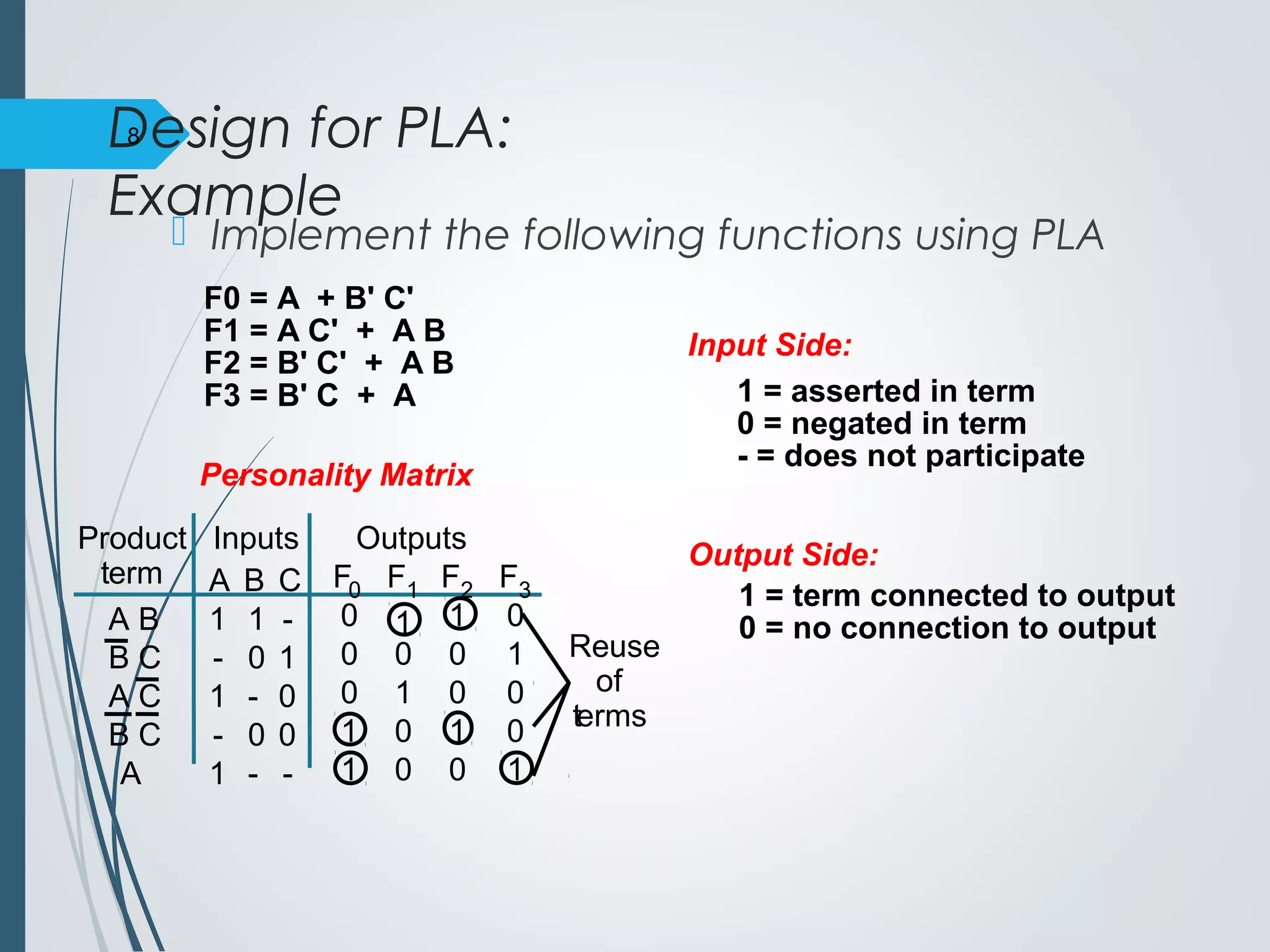
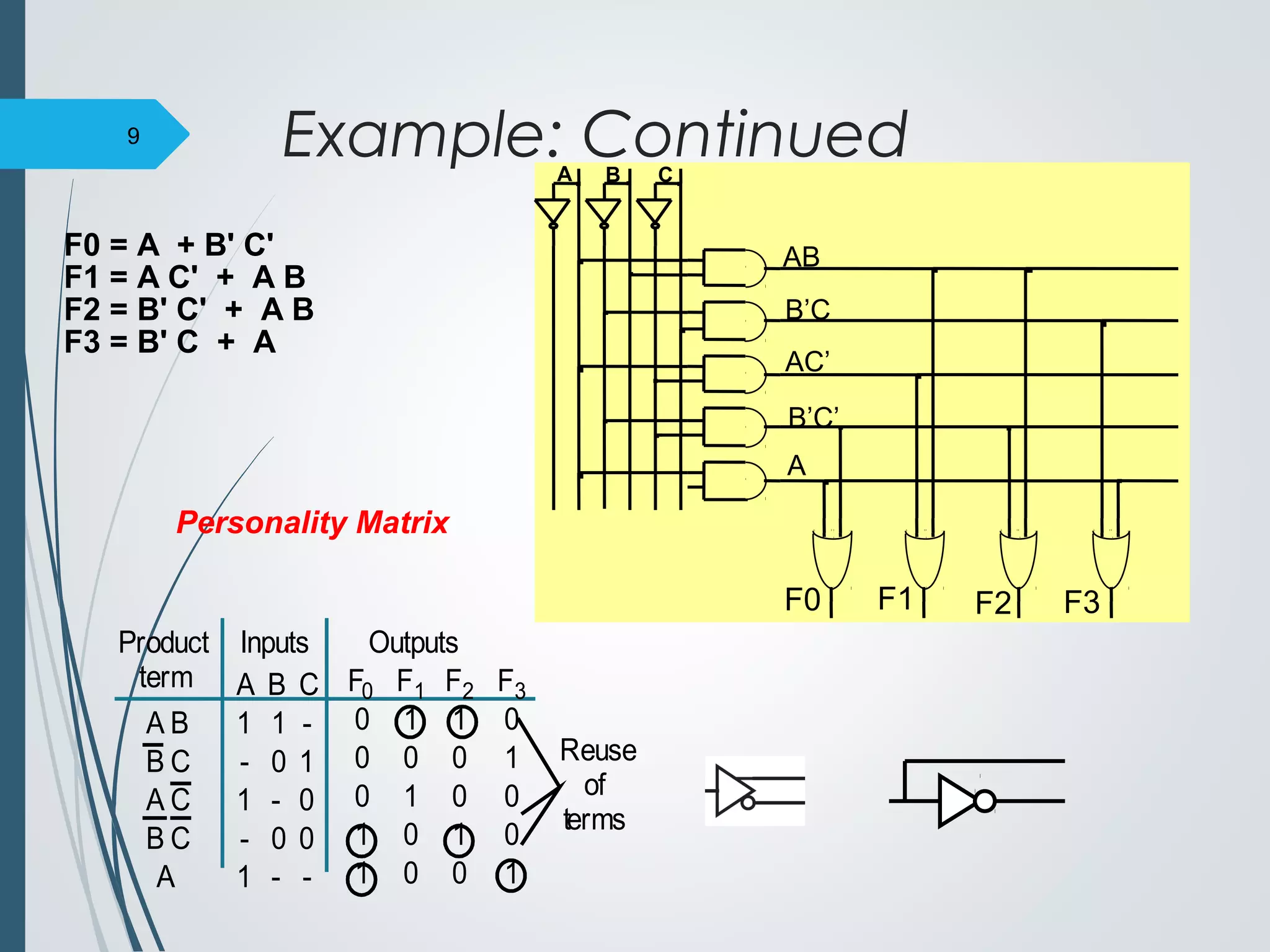
1. Programmable Logic Arrays (PLAs) are pre-fabricated logic blocks containing AND and OR gates that can be personalized by making or breaking connections between gates. This allows them to implement general purpose logic functions. 2. An example shows a 3x2 PLA implementing 4 logic functions through a personality matrix that defines which inputs are connected to each product term and which product terms are connected to each output. 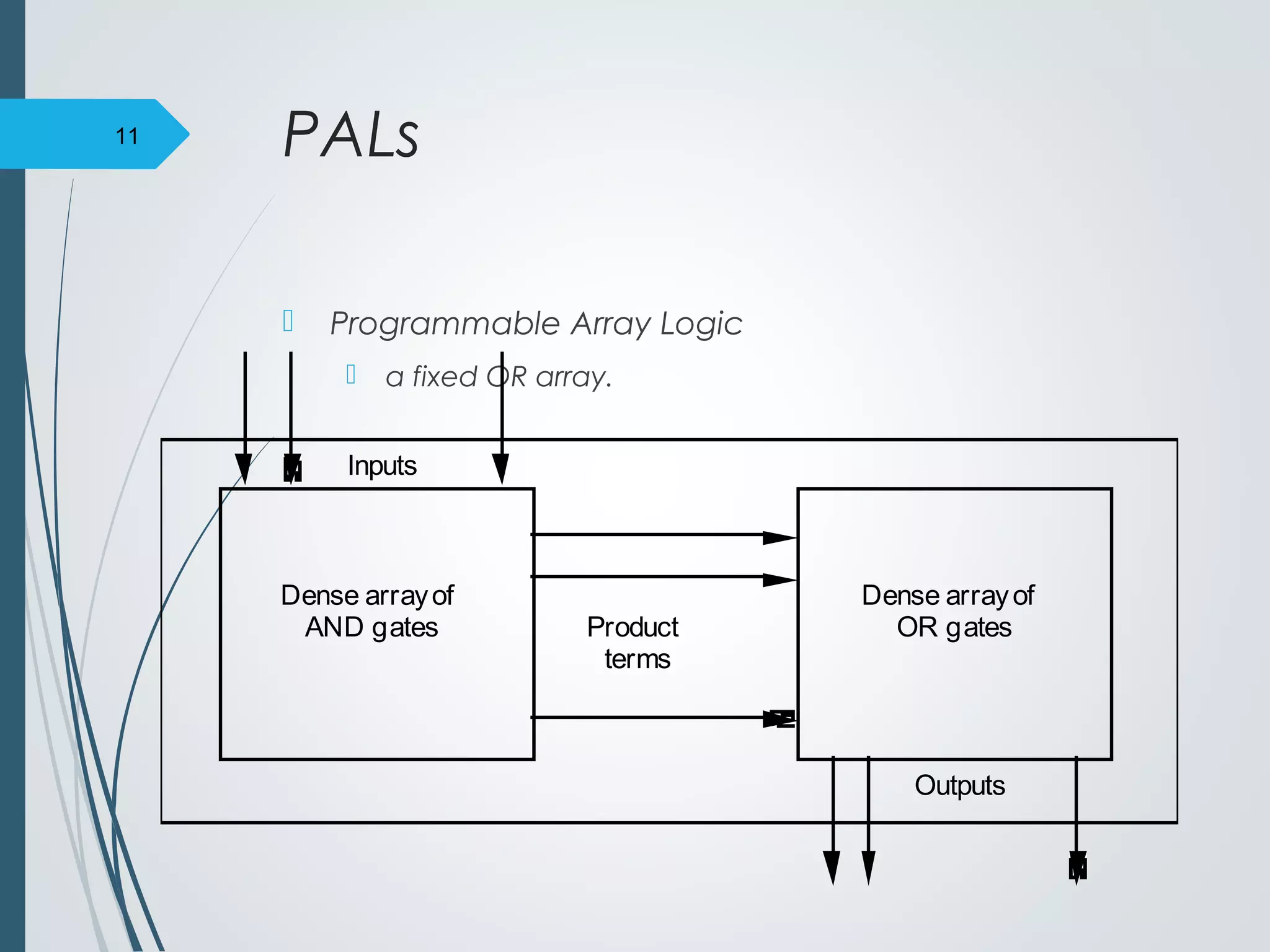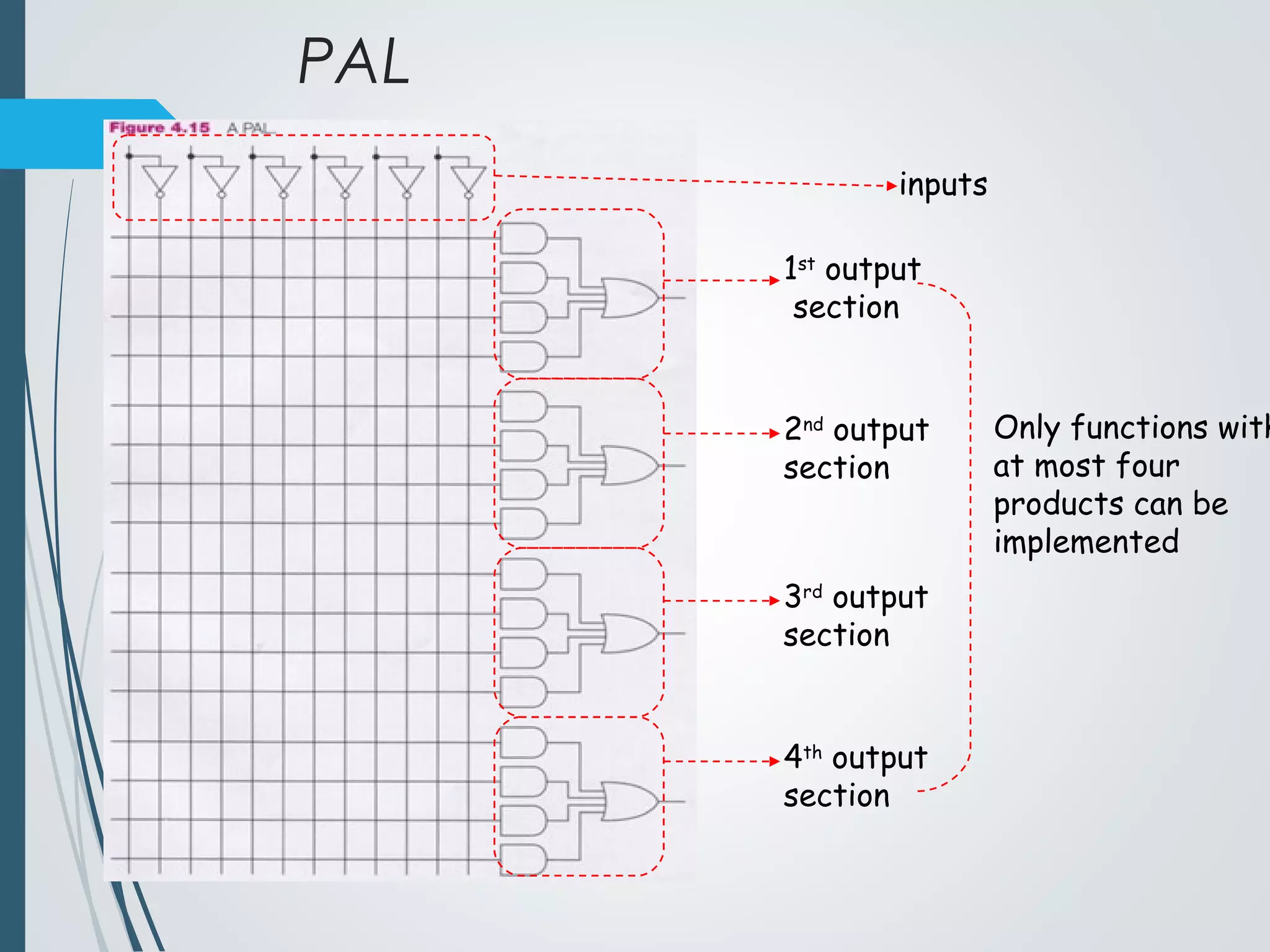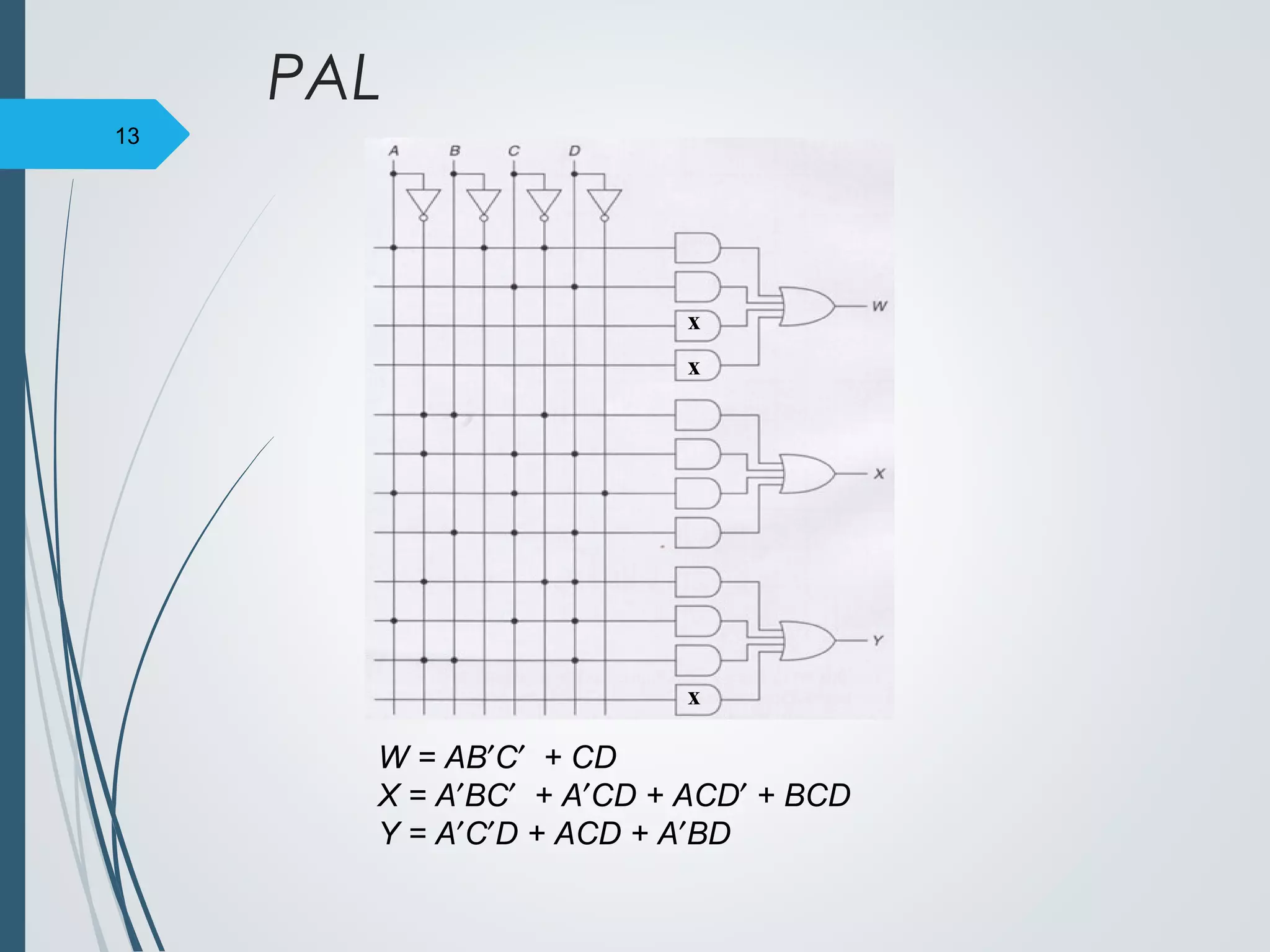3. PALs (Programmable Array Logic) are similar to PLAs but contain a fixed OR array, limiting them to functions with at most 4 products.

1. 1

2. 2

3. Programmable Logic
PAL, PLA

4. PLAs
Programmable Logic Array
 Pre-fabricated building block of
many AND/OR gates (or NOR, NAND)
"Personalized" by making/ breaking
connections among the gates.
 General purpose logic building
blocks.
4

5. PLA5
Inputs
Dense arrayof
AND gates Product
terms
Dense arrayof
OR gates
Outputs

6. PLA
6

7. PLA7
• A 3×2 PLA with 4 product terms.

8. Design for PLA:
Example
 Implement the following functions using PLA
8
F0 = A + B' C'
F1 = A C' + A B
F2 = B' C' + A B
F3 = B' C + A
Personality Matrix
1 = asserted in term
0 = negated in term
- = does not participate
Input Side:
1 = term connected to output
0 = no connection to output
Output Side:
OutputsInputsProduct
term
Reuse
of
terms
A
1
-
1
-
1
B
1
0
-
0
-
C
-
1
0
0
-
F0
0
0
0
1
1
F1
1
0
1
0
0
F2
1
0
0
1
0
F3
0
1
0
0
1
A B
B C
A C
B C
A

9. Example: Continued9
F0 = A + B' C'
F1 = A C' + A B
F2 = B' C' + A B
F3 = B' C + A
Personality Matrix
OutputsInputsProduct
term
Reuse
of
terms
A
1
-
1
-
1
B
1
0
-
0
-
C
-
1
0
0
-
F0
0
0
0
1
1
F1
1
0
1
0
0
F2
1
0
0
1
0
F3
0
1
0
0
1
A B
B C
A C
B C
A
A B C
F0 F1 F2 F3
AB
B’C
AC’
B’C’
A

10. Constants
 Sometimes a PLA output
must be programmed
to be a constant 1 or a
constant 0.
 P1 is always 1
because its product
line is connected to
no inputs and is
therefore always
pulled HIGH;
 this constant-1 term
drives the O1 output.
 No product term drives
the O2 output, which is
therefore always 0.
 Another method of
obtaining a constant-0
output is shown for O3.
10

11. PALs
 Programmable Array Logic
 a fixed OR array.
11
Inputs
Dense arrayof
AND gates Product
terms
Dense arrayof
OR gates
Outputs

12. PAL
12
inputs
1st
output
section
2nd
output
section
3rd
output
section
4th
output
section
Only functions with
at most four
products can be
implemented

13. PAL
13
W = AB′C′ + CD
X = A′BC′ + A′CD + ACD′ + BCD
Y = A′C′D + ACD + A′BD
x
x
x

14. 14

15. 15