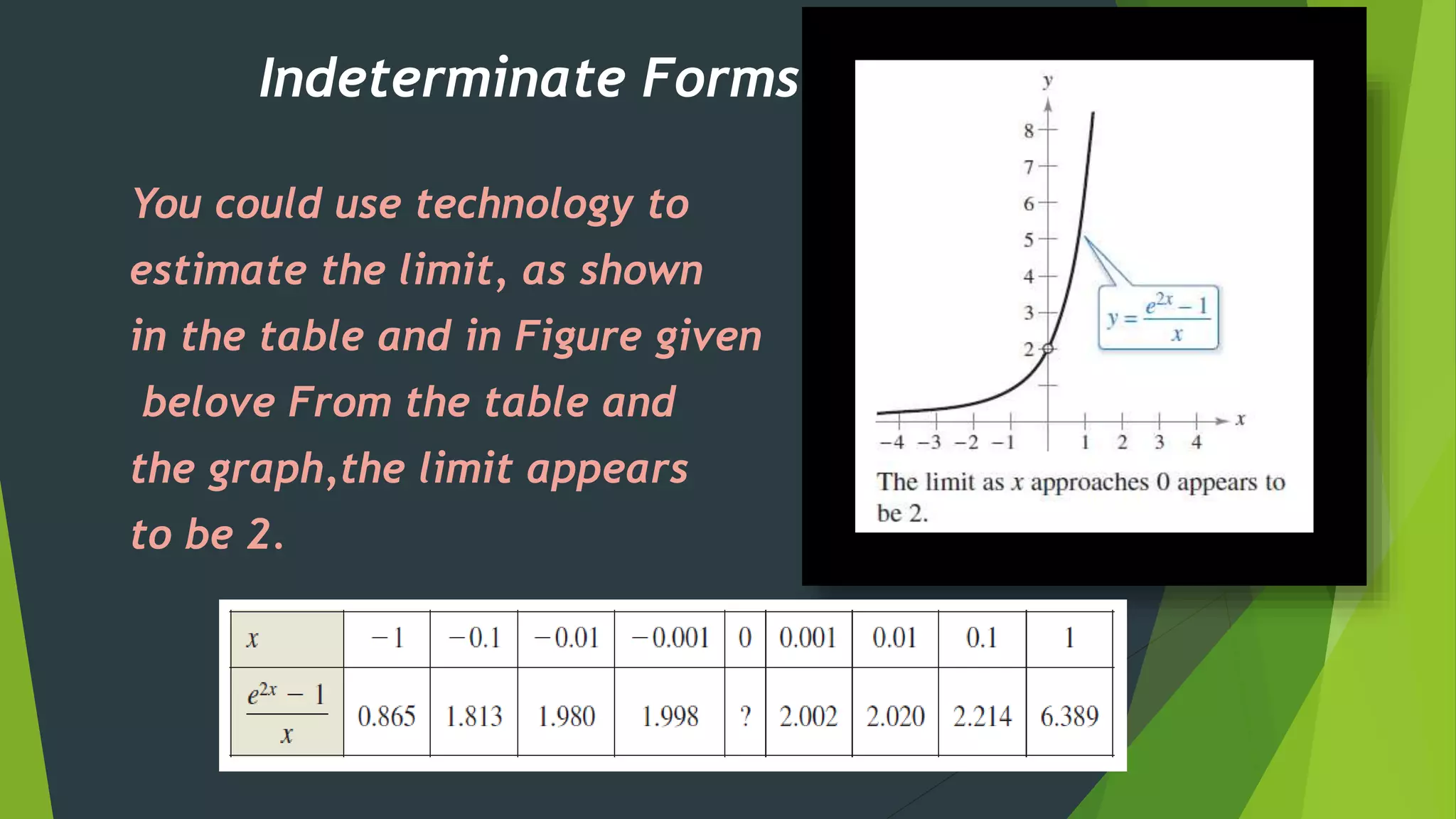
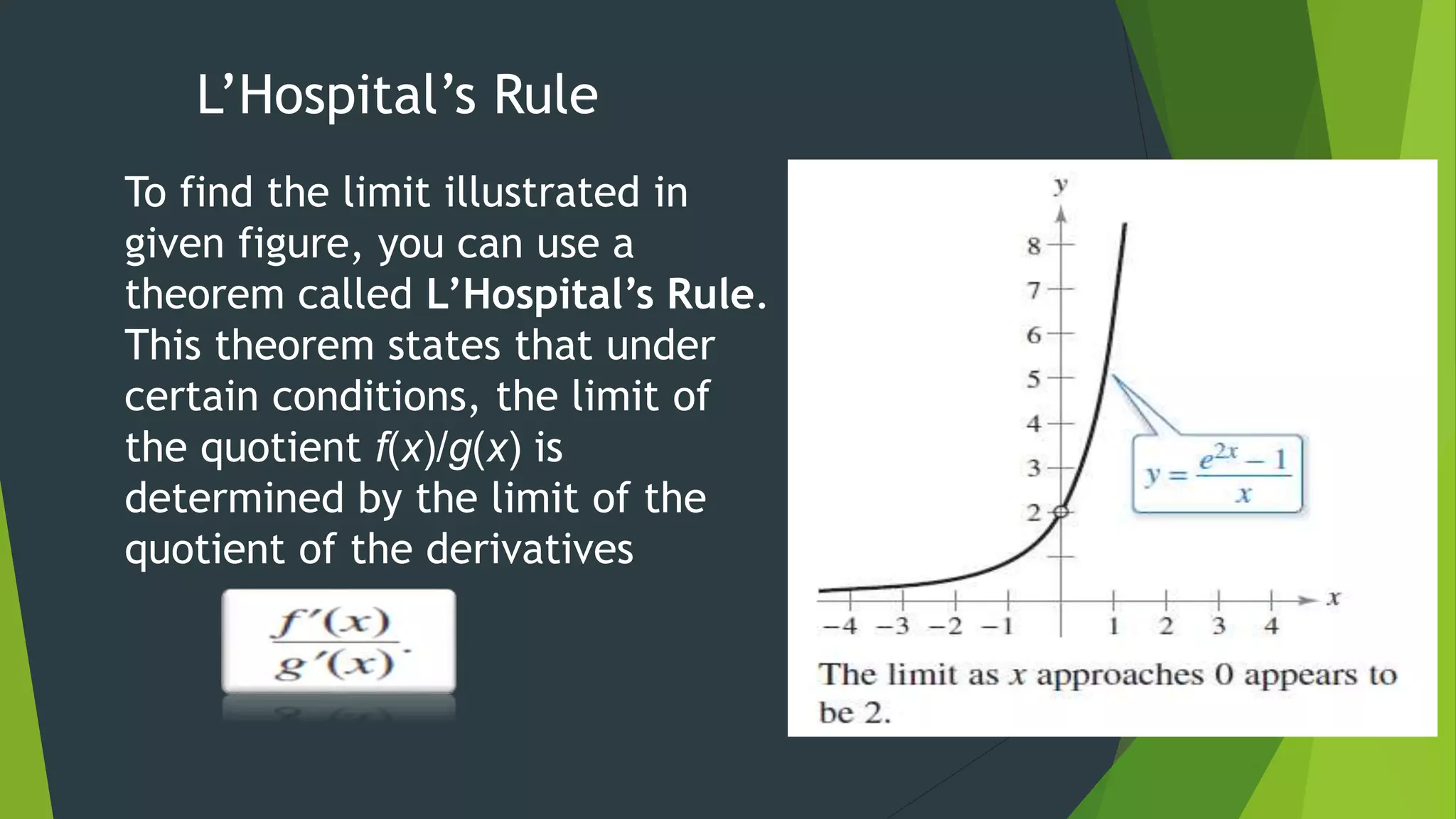
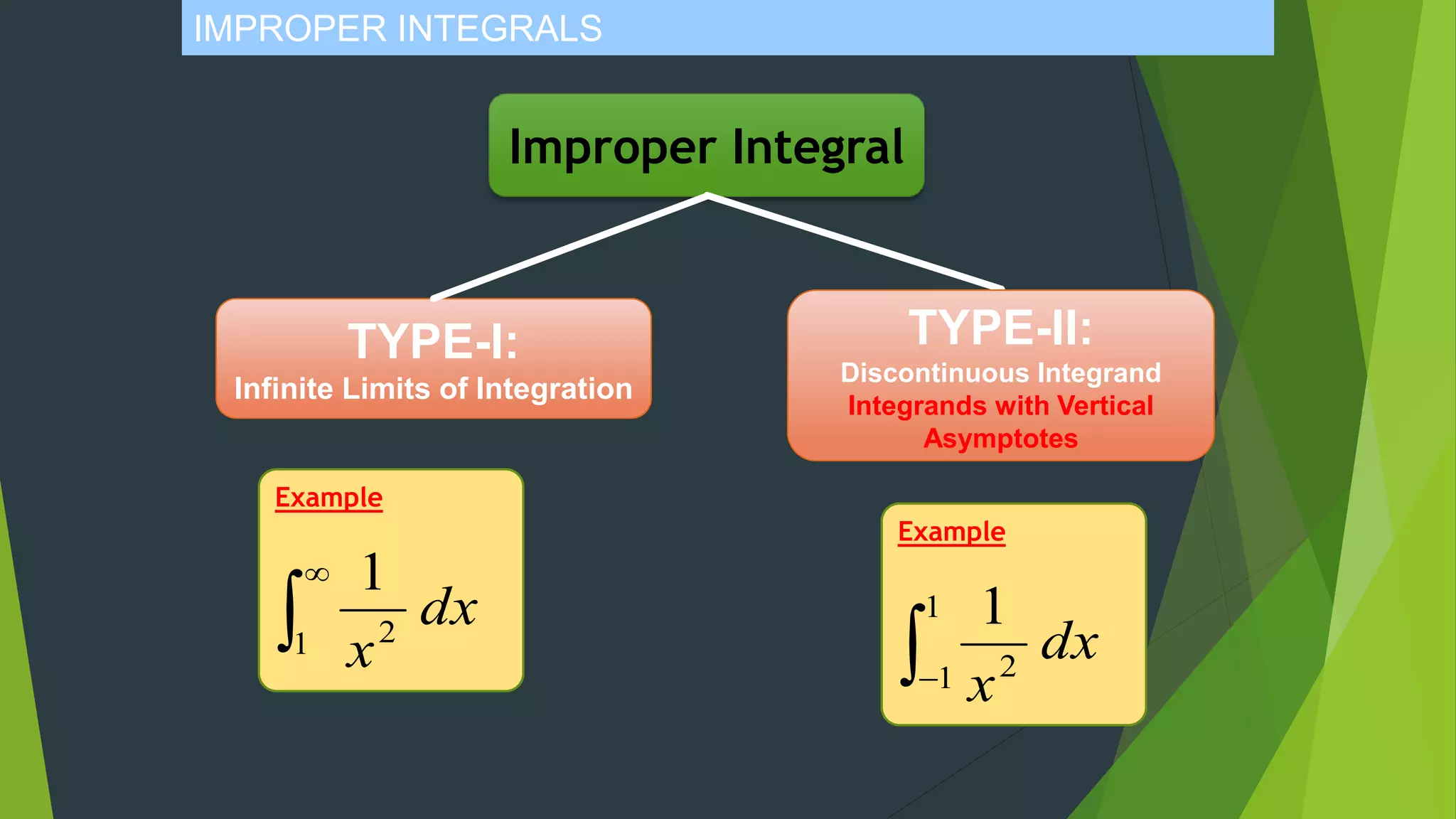
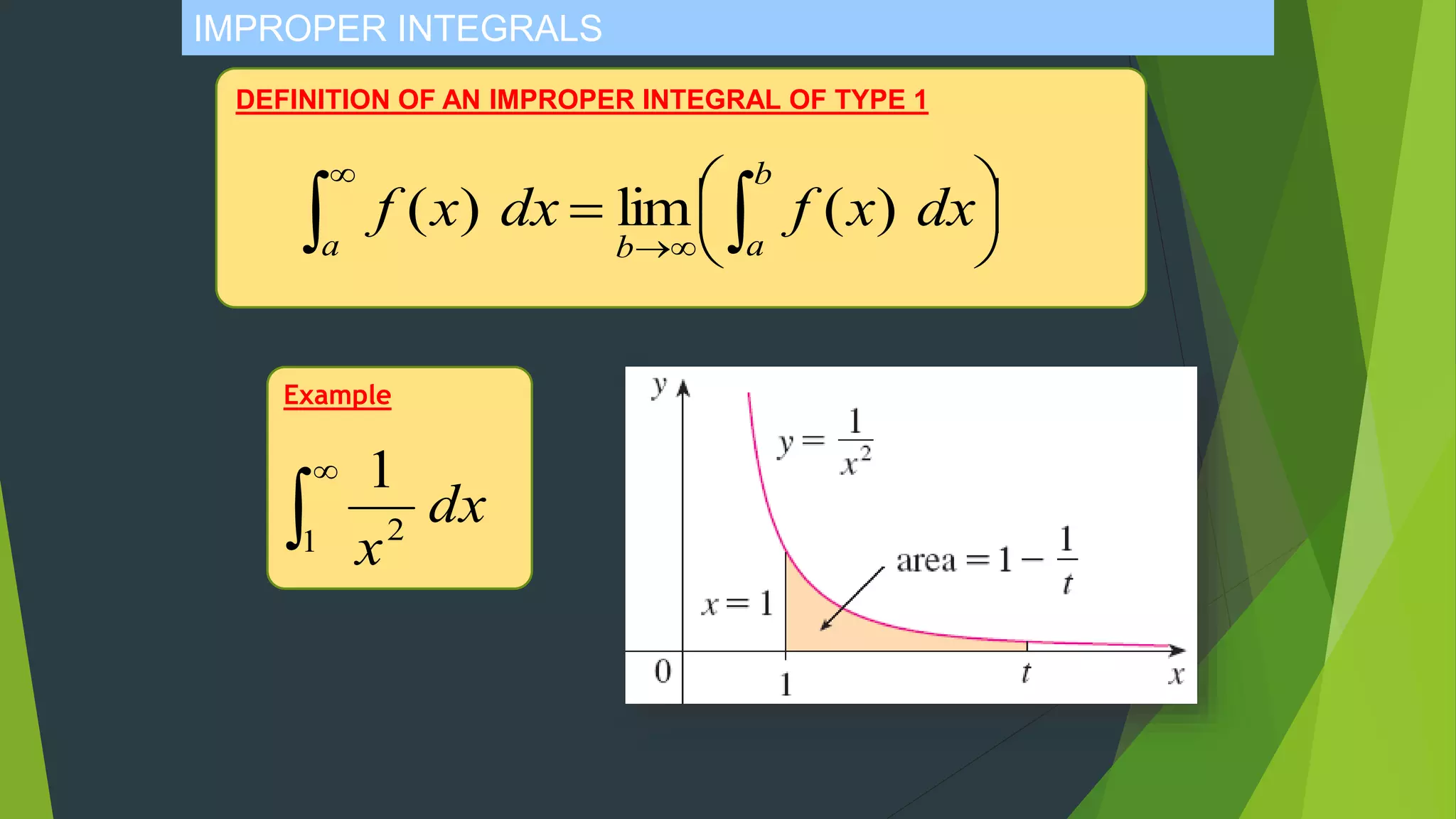
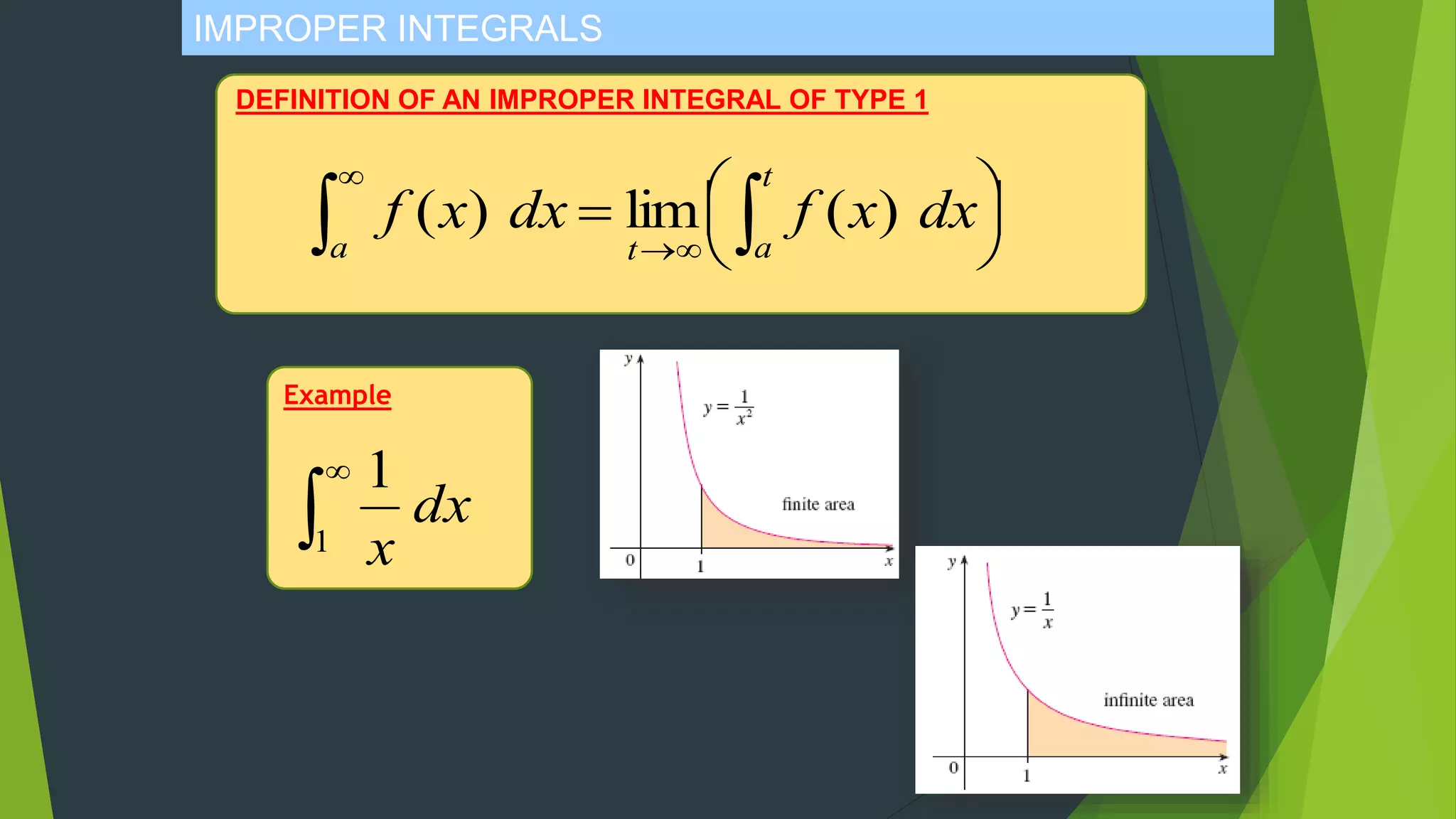
The document discusses indeterminate forms and improper integrals. It begins by defining indeterminate forms as limits that produce 0/0 or infinity/infinity, which do not guarantee a limit exists or indicate its value. It introduces L'Hopital's Rule, which can be used to evaluate certain indeterminate forms by taking the limit of the quotient of the derivatives. The document then defines improper integrals as integrals with infinite limits of integration or discontinuous integrands, and provides examples of how to calculate them.

2. 44
Ronak Sutariya

3. Inderminate forms
and improper
integrals

4. objectives
 Recognize limits that produce indeterminate forms.
 Apply L’Hôpital’s Rule to evaluate a limit.

5. Indeterminate Forms
The forms 0/0 and are called indeterminate because they
do not guarantee that a limit exists, nor do they indicate what
the limit is, if one does exist.
When you encountered one of these indeterminate forms earlier in
the text, you attempted to rewrite the expression by using
various algebraic techniques.

6. Indeterminate Forms
 Occasionally, you can extend these algebraic techniques
to find limits of transcendental functions. For instance,
the limit
 produces the indeterminate form 0/0. Factoring and then dividing produces

7. Indeterminate Forms
Not all indeterminate forms, however, can be evaluated by algebraic
manipulation. This is often true when both algebraic and transcendental
functions are involved.
For instance, the limit
produces the indeterminate form 0/0.
Rewriting the expression to obtain
merely produces another indeterminate form,

8. Indeterminate Forms
You could use technology to
estimate the limit, as shown
in the table and in Figure given
belove From the table and
the graph,the limit appears
to be 2.

9. L’Hospital’s Rule
To find the limit illustrated in
given figure, you can use a
theorem called L’Hospital’s Rule.
This theorem states that under
certain conditions, the limit of
the quotient f(x)/g(x) is
determined by the limit of the
quotient of the derivatives

10. Example 1 – Indeterminate Form 0/0
Evaluate
Solution:
Because direct substitution results in the
indeterminate form 0/0.

11. Example 1 – Solution
You can apply L’Hospital’s Rule, as shown
below.

12. L’Hospital’s Rule
The forms have
been identified as indeterminate. There are similar forms
that you should recognize as “determinate.”
As a final comment, remember that L’Hôpital’s Rule can be
applied only to quotients leading to the indeterminate forms
0/0 and

13. Example
IMPROPER INTEGRALS
Improper Integral
TYPE-I:
Infinite Limits of Integration


1 2
1
dx
x
Example

1
1 2
1
dx
x
TYPE-II:
Discontinuous Integrand
Integrands with Vertical
Asymptotes

14. IMPROPER INTEGRALS
DEFINITION OF AN IMPROPER INTEGRAL OF TYPE 1




  
 b
aba
dxxfdxxf )(lim)(
Example


1 2
1
dx
x

15. IMPROPER INTEGRALS
DEFINITION OF AN IMPROPER INTEGRAL OF TYPE 1




  
b
aa
b
dxxfdxxf )(lim)(
Example
 
0
dxxex

16. IMPROPER INTEGRALS
DEFINITION OF AN IMPROPER INTEGRAL OF TYPE 1




  
b
aa
b
dxxfdxxf )(lim)(




  
 b
aba
dxxfdxxf )(lim)(
The improper integrals
are called convergent if the corresponding limit exists
and divergent if the limit does not exist.


a
dxxf )(
 
a
dxxf )(

17. IMPROPER INTEGRALS
DEFINITION OF AN IMPROPER INTEGRAL OF TYPE 1




  
 t
ata
dxxfdxxf )(lim)(
Example


1
1
dx
x

18. IMPROPER INTEGRALS
DEFINITION OF AN IMPROPER INTEGRAL OF TYPE 1



dxxf )(
If both improper integrals
are convergent


a
dxxf )(  
a
dxxf )(
convergent



dxxf )( 



a
a
dxxfdxxf )()(
Example


 
dx
x 1
1
2

19. DEFINITION OF AN IMPROPER
INTEGRAL OF TYPE 2
Example
 
5
2
2
1
dx
x

20. Ronak Sutariya