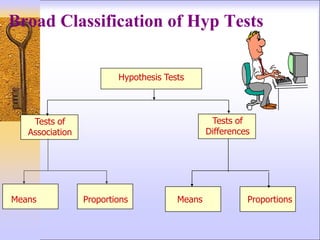
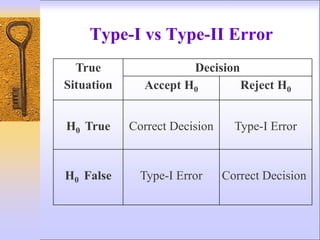
1) Hypothesis testing involves making an educated guess about a population parameter and designing a study to analyze sample data to determine if the population characteristic is likely or unlikely. 2) The null hypothesis states what is assumed to be true about the population parameter, while the alternative hypothesis is what would be accepted if the null is rejected. Type I and Type II errors occur when the wrong conclusion is reached. 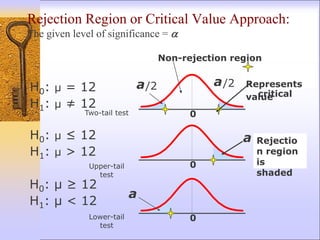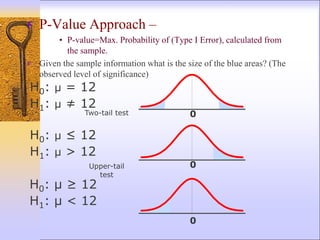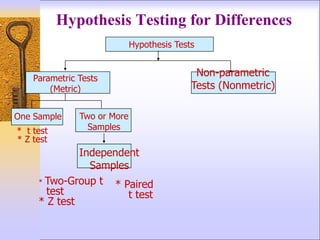3) Key aspects of hypothesis testing include defining the test statistic, rejection region, significance level, and whether a one-tailed or two-tailed test is appropriate based on the alternative hypothesis.

1. Hypothesis Testing

2. What is Hypothesis
• Hypothesis
• An educated guess
• A claim or statement about a property of
a population which may or may not be
true.
• The goal in Hypothesis Testing is to analyze a
sample in an attempt to distinguish between
population characteristics that are likely to
occur and population characteristics that are
unlikely to occur.

3. • Null Hypothesis vs.
Alternative
Hypothesis
• Type I vs. Type II
Error
The Basics

4. Null Hypothesis vs. Alternative
Hypothesis
Null Hypothesis
• Statement about the
value of a population
parameter
• Represented by H0
• Always stated as an
Equality
• It is hypothesis of no
effect
Alternative Hypothesis
• Statement about the value
of a population parameter
that must be accepted if the
null hypothesis is rejected
• Represented by H1
• Stated in one of three
forms
• >
• <
• 

5. Type-I vs Type-II Error
Type-I Error
• Rejecting null
hypothesis (H0) when
H0 is actually true.
• It is denoted by α
• α = probability of a
Type I error
Type-I Error
• Accepting null hypothesis
(H0) when H0 is actually
false.
• It is denoted by β
• β = probability of a Type-
II error

6. Type-I vs Type-II Error
True
Situation
Decision
Accept H0 Reject H0
H0 True Correct Decision Type-I Error
H0 False Type-I Error Correct Decision

7. Example
• In a court trial, the supposition of Law is that the accused
(the defendant) is innocent. This supposition may be
regarded as a kind of null hypothesis H0 that is to be
rejected or accepted.
• Suppose the accused is in fact innocent (i-e H0 is true),
but finding of the judge is guilty. He has rejected the true
null hypothesis and has made a Type-I Error.
• If, on the other hand, the accused is in fact guilty (i-e H0
is false), but finding of the judge is innocent. He has
accepted the false null hypothesis and has committed a
Type-II Error.

8. Alpha
 a is the probability of Type I error
 The experimenters (you and I) have the freedom to
set the -level for a particular hypothesis test.
That level is called the level of significance for
the test. Changing a can (and often does) affect
the results of the test—whether you reject or fail
to reject H0.

9. Test Statistic and Rejection
Region
• Test Statistic: The sample statistic on which we
base our decision to reject or not reject the null
hypothesis.
• Rejection Region: Range of values such that, if
the test statistic falls in that range, we will decide
to reject the null hypothesis, otherwise, we will
not reject the null hypothesis.

10. Rejection Region or Critical Value Approach:
The given level of significance = 
H0: μ ≥ 12
H1: μ < 12
0
H0: μ ≤ 12
H1: μ > 12
a
a
Represents
critical
value
Lower-tail
test
0
Upper-tail
test
Two-tail test
Rejectio
n region
is
shaded
/2
0
a
/2
a
H0: μ = 12
H1: μ ≠ 12
Non-rejection region

11. F P-Value Approach –
• P-value=Max. Probability of (Type I Error), calculated from
the sample.
F Given the sample information what is the size of the blue areas? (The
observed level of significance)
H0: μ ≥ 12
H1: μ < 12
H0: μ ≤ 12
H1: μ > 12
0
Upper-tail
test
Two-tail test 0
H0: μ = 12
H1: μ ≠ 12
0

12. One-tailed & Two-tailed Tests
One-tailed Test
• A test for which entire
rejection region is located
in only one of the two
tails- either in right tail or
in left tail of sampling
distribution of test-
statistic.
• A one-tailed test is used
when alternative
hypothesis is formulated
as
H1 : Ɵ > Ɵ0
H1 : Ɵ < Ɵ0
Two-tailed Test
• A test for which the
rejection region is divided
equally between the two
tails of the sampling
distribution of test-
statistic. In this case, the
alternative hypothesis is
set up as:
H1 : Ɵ  Ɵ0

13. When do we use a two-tail test?
when do we use a one-tail test?
F The answer depends on the question you are trying to
answer.
F A two-tail is used when the researcher has no idea
which direction the study will go, interested in both
direction. (example: testing a new technique, a new product, a new theory and
we don’t know the direction)
F A new machine is producing 12 fluid once can of soft drink. The quality control
manager is concern with cans containing too much or too little. Then, the test is a two-
tailed test. That is the two rejection regions in tails is most likely (higher probability) to
provide evidence of H1.
oz
12
:
H
oz
12
:
H
1
0





1
2

14. F One-tail test is used when the researcher is interested in the
direction.
F Example: The soft-drink company puts a label on cans
claiming they contain 12 oz. A consumer advocate desires
to test this statement. She would assume that each can
contains at least 12 oz and tries to find evidence to the
contrary. That is, she examines the evidence for less than
12 0z.
F What tail of the distribution is the most logical (higher
probability) to find that evidence? The only way to reject
the claim is to get evidence of less than 12 oz, left tail.
oz
12
:
H
oz
12
:
H
1
0





1
2
1
4
11.5

15. Broad Classification of Hyp Tests
Means Proportions
Tests of
Association
Tests of
Differences
Hypothesis Tests
Means Proportions

16. Hypothesis Testing for Differences
Independent
Samples
* Two-Group t
test
* Z test
* Paired
t test
Hypothesis Tests
One Sample Two or More
Samples
* t test
* Z test
Parametric Tests
(Metric)
Non-parametric
Tests (Nonmetric)

17. Test of Hypothesis for the Mean
The test statistic is:
n
S
μ
X
t 1
-
n


σ Unknown
σ known
The test statistic is:
n
σ
μ
X
Z



18. Seven Steps to Hypothesis
Testing

19. 1) Describe in words the population
characteristic about which hypotheses are to
be tested
2) State the null hypothesis, Ho
3) State the alternative hypothesis, H1 or Ha
4) Display the test statistic to be used
The Seven Steps…

20. 5) Identify the rejection region
• Is it an upper, lower, or two-tailed
test?
• Determine the critical value
associated with , the level of
significance of the test
6) Compute all the quantities in the test
statistic, and compute the test statistic
itself
The Seven Steps…

21. The Seven Steps…
7) State the conclusion.
• That is, decide whether to reject the null
hypothesis, Ho, or fail to reject the null
hypothesis. The conclusion depends on the
level of significance of the test. Also,
remember to state your result in the context of
the specific problem.

22. Interpreting the p-value…
• The smaller the p-value, the more statistical
evidence exists to support the alternative
hypothesis.
• If the p-value is less than 1%, there is
overwhelming evidence that supports the
alternative hypothesis.
• If the p-value is between 1% and 5%, there is a
strong evidence that supports the alternative
hypothesis.

23. 11.23
Interpreting the p-value…
• If the p-value is between 5% and 10% there is a
weak evidence that supports the alternative
hypothesis.
• If the p-value exceeds 10%, there is no evidence
that supports the alternative hypothesis.
• We observe a p-value of .0069, hence there is
overwhelming evidence to support H1: >170.