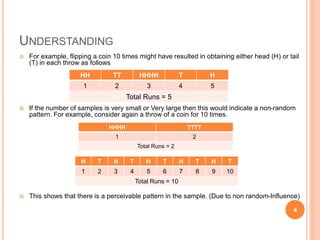
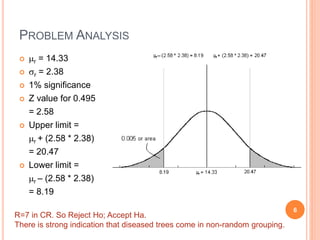
This document discusses a one sample runs test, which is used to determine if a sample is randomly drawn from a population. It defines a run as a series of like items. The document provides an example of coin flips and illustrates how different outcomes would indicate random or non-random patterns. It presents the formula for the runs test and applies it to an example of testing if diseased trees are randomly or non-randomly grouped. The requirements, advantages, and other applications of the runs test are outlined.

1. ONE SAMPLE RUNS TEST
Milind Gokhale
Nilesh Kataria
Kiran Itagi
Pratik Sharma
Rohit Murari
1

2. AGENDA
 Purpose of test and terminology
 Understanding Basic
 Formulae
 Problem
 Problem Analysis
 Requirements for One sample runs test
 Advantages
 Other applications
2

3. PURPOSE OF THE TEST AND TERMINOLOGY
 Quite often in research we may be interested in
finding out whether the sample is drawn at random,
so that we can generalise the sample results to the
population
 we can apply the technique called ‘Runs test’,
which is exclusively used for the purpose of
ensuring the randomness of parameters of interest
 “Run” is defined as a ‘series of like items‘.
3

4. UNDERSTANDING
 For example, flipping a coin 10 times might have resulted in obtaining either head (H) or tail
(T) in each throw as follows
 If the number of samples is very small or Very large then this would indicate a non-random
pattern. For example, consider again a throw of a coin for 10 times.
 This shows that there is a perceivable pattern in the sample. (Due to non random-Influence)
HH TT HHHH T H
1 2 3 4 5
Total Runs = 5
HHHH TTTT
1 2
Total Runs = 2
H T H T H T H T H T
1 2 3 4 5 6 7 8 9 10
Total Runs = 10
4

5. FORMULAE
 mr = (2n1n2 / n1+n2) +1
PROBLEM
 H= Healthy Tree D= Diseased Tree
 H0 = The trees are planted/placed randomly
 Ha = Diseased trees come in non-random grouping
HH DD HHHH DDD HHHH DDDDD HHHHHHHHH
1 2 3 4 5 6 7
Total Runs = 7
5

6. PROBLEM ANALYSIS
 mr = 14.33
 sr = 2.38
 1% significance
 Z value for 0.495
= 2.58
 Upper limit =
mr + (2.58 * 2.38)
= 20.47
 Lower limit =
mr – (2.58 * 2.38)
= 8.19
R=7 in CR. So Reject Ho; Accept Ha.
There is strong indication that diseased trees come in non-random grouping.
6

7. REQUIREMENTS
 This checks for randomness of the sample
selected.
 It is highly useful in checking the randomness of
residuals in regression or time series and
forecasting models.
ADVANTAGES
 This test checks for randomness of the sample
selected.
 It is highly useful in checking the randomness of
residuals in regression or time series and
forecasting models. 7

8. OTHER APPLICATIONS
 Thus a runs test is used to test the randomness
dichotomous observations like head/tail, yes/no,
men/women, married/single, high/low,
increasing/decreasing
 Possibly in stock market technical analyses or
Forecasting and Analyses.
 In time series analyses finding out whether the errors
(residuals) of the models are randomly distributed
 finding out the randomness of defective items in the
quality control process 8