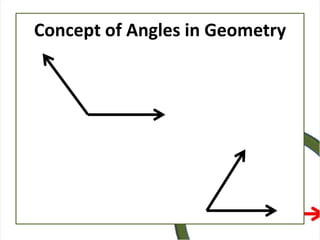
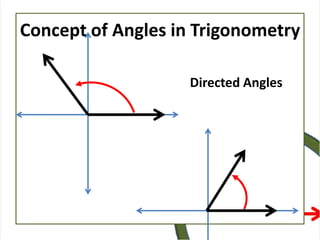
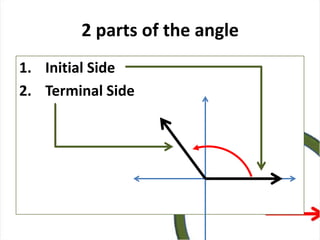
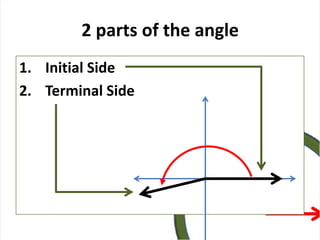
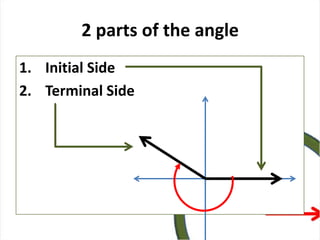
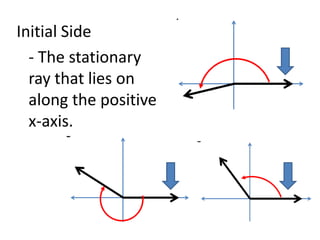
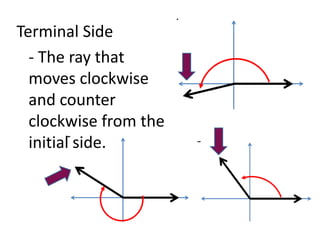
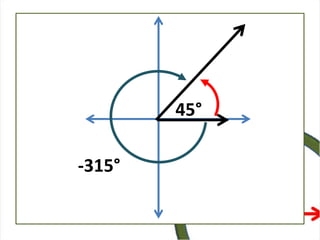
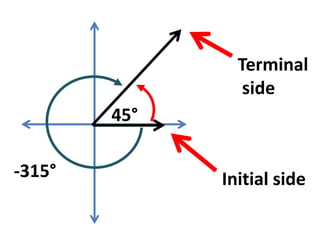
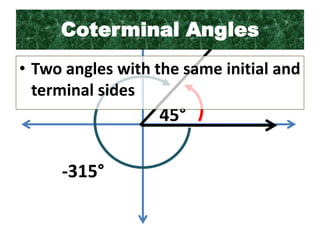
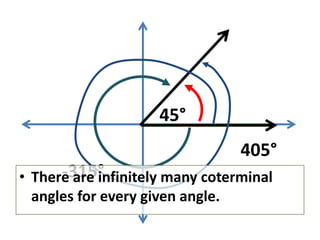
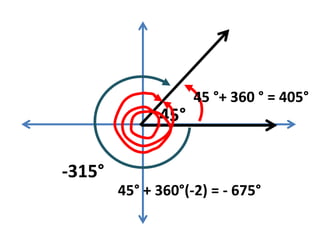
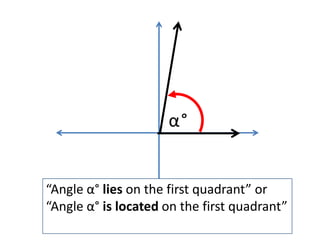
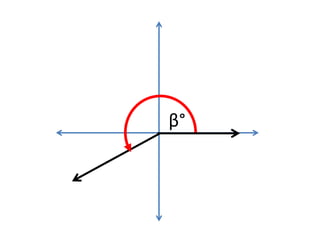
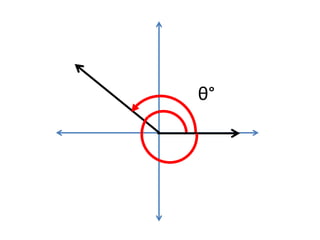
This document defines angles and angle measure in geometry and trigonometry. It explains that an angle is formed by two rays with a common endpoint, and can be measured in degrees from 0 to 360 degrees. The document discusses angle terminology like initial side, terminal side, standard position, coterminal angles, quadrantal angles, and locating angles by quadrant. It provides examples of finding coterminal angles and sketching angles in standard position. Exercises at the end have the reader practice finding coterminal angles, sketching angles, and determining angle locations.

2. Angles and Angle Measure

3. Is this an angle? Is this an angle?
Is this an angle?

4. Trigonometry
• Trigonometry is the
study of triangles and
the relationship
among their sides and
angles.

5. T r i g o n o m e t r y
• “gono” – angle
• “tria” - three
• “metria” - measure

6. Angles
An angle is formed by two rays,
one moving and one stationary that
have the same endpoint.

7. Concept of Angles in Geometry

8. Concept of Angles in Trigonometry
Directed Angles

9. 2 parts of the angle
1. Initial Side
2. Terminal Side

10. 2 parts of the angle
1. Initial Side
2. Terminal Side

11. 2 parts of the angle
1. Initial Side
2. Terminal Side

12. Initial Side
- The stationary
ray that lies on
along the positive
x-axis.

13. Terminal Side
- The ray that
moves clockwise
and counter
clockwise from the
initial side.

14. Angle on Standard Position
• An angle is in standard position if its
vertex coincides with the origin of
the coordinate plane and its initial
side coincides with the positive x –
axis.

15. 45°
-315°

16. • Positive angles are generated by
counterclockwise rotations and
negative angles are generated by
clockwise rotations.
• Angles are often named by Greek
letters such as α (Alpha), β (Beta), θ
(Theta)

17. 45°
-315° Initial side
Terminal
side

18. 45°
-315°
Coterminal Angles
• Two angles with the same initial and
terminal sides

19. 45°
-315°
405°
• There are infinitely many coterminal
angles for every given angle.

20. To find a coterminal angle,
• Use the formula:
Where:
θ1 is the coterminal angle
θ is the given angle
n is the number of positive or
negative revolutions
n3601
revolutions

21. Example:
• Find one positive after one revolution and one
negative coterminal after 2 revoltuions of 45
degrees.

22. 45°
-315°
45 °+ 360 ° = 405°
45° + 360°(-2) = - 675°

23. Angle Location
• If the terminal side of an angle lies in
a given quadrant, then the angle is
said to lie in that quadrant.

24. α°
“Angle α° lies on the first quadrant” or
“Angle α° is located on the first quadrant”

25. β°

26. θ°

27. Angle Location
• If the terminal side of an angle in
standard position coincides with a
coordinate axis, then the angle is
called a quadrantal angle.

29. Exercises

30. A. Sketch the following angles in
standard position. (3 pts. each)
1. -115°
2. 75°
B. Tell the location of each angle. (2
pts. each)
1. 70°
2. 195°

31. C. Find the coterminal angles of the ff.
by adding two positive and one
negative revolution. (2 pts. each)
1. 350° __________ __________
2. - 25° __________ __________
3. 125° __________ __________
4. - 76° __________ __________
5. 80° __________ __________

32. Answer key for C
• 1070, -10
• 695, -385
• 845, -235
• 644, -436
• 800, -280

33. Assignment:
Note: One revolution = 360°
1. Sketch the angle in standard
position: ¾ revolution (5 pts.)
2. Tell the location of the angle in
standard position: -(3/5)
revolution. (5 points)
3. Bring a protractor tomorrow.