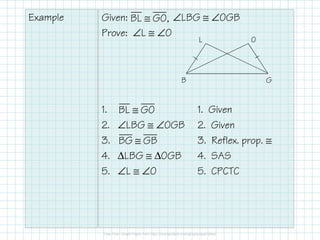
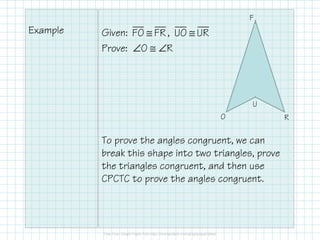
This document discusses the concept of CPCTC (Corresponding Parts of Congruent Triangles are Congruent). It states that once two triangles are proven to be congruent using SSS, SAS, ASA, AAS, or HL, then all corresponding parts of those triangles are also congruent due to CPCTC. It provides two examples of using CPCTC to prove corresponding angles are congruent after first showing the triangles are congruent using given information.

1. Obj. 19 CPCTC
The student will be able to (I can):
• Show that corresponding parts of congruent triangles are
congruent.
• Use CPCTC to solve problems

2. CPCTC
An abbreviation for “Corresponding Parts of
Congruent Triangles are Congruent.”
Once we know two triangles are congruent,
we then know that all of their corresponding
sides and angles are congruent.
To use CPCTC, first prove the triangles
congruent using SSS, SAS, ASA, AAS, or
HL, and then use CPCTC to state that the
other parts of the triangle are also
congruent.

3. Example
Given: BL ≅ GO, ∠LBG ≅ ∠OGB
Prove: ∠L ≅ ∠O
L
O
B
1.
2.
3.
4.
5.
G
BL ≅ GO
∠LBG ≅ ∠OGB
BG ≅ GB
∆LBG ≅ ∆OGB
∠L ≅ ∠O
1. Given
2. Given
3. Reflex. prop. ≅
4. SAS
5. CPCTC

4. F
Example
Given: FO ≅ FR , UO ≅ UR
Prove: ∠O ≅ ∠R
U
O
To prove the angles congruent, we can
break this shape into two triangles, prove
the triangles congruent, and then use
CPCTC to prove the angles congruent.
R

5. F
Example:
Given: FO ≅ FR , UO ≅ UR
Prove: ∠O ≅ ∠R
U
O
Statements
Reasons
1. FO ≅ FR
1. Given
2. UO ≅ UR
3. UF ≅ UF
2. Given
4.
FOU ≅ FRU
5. ∠O ≅ ∠R
3. Refl. prop. ≅
4. SSS
5. CPCTC
R