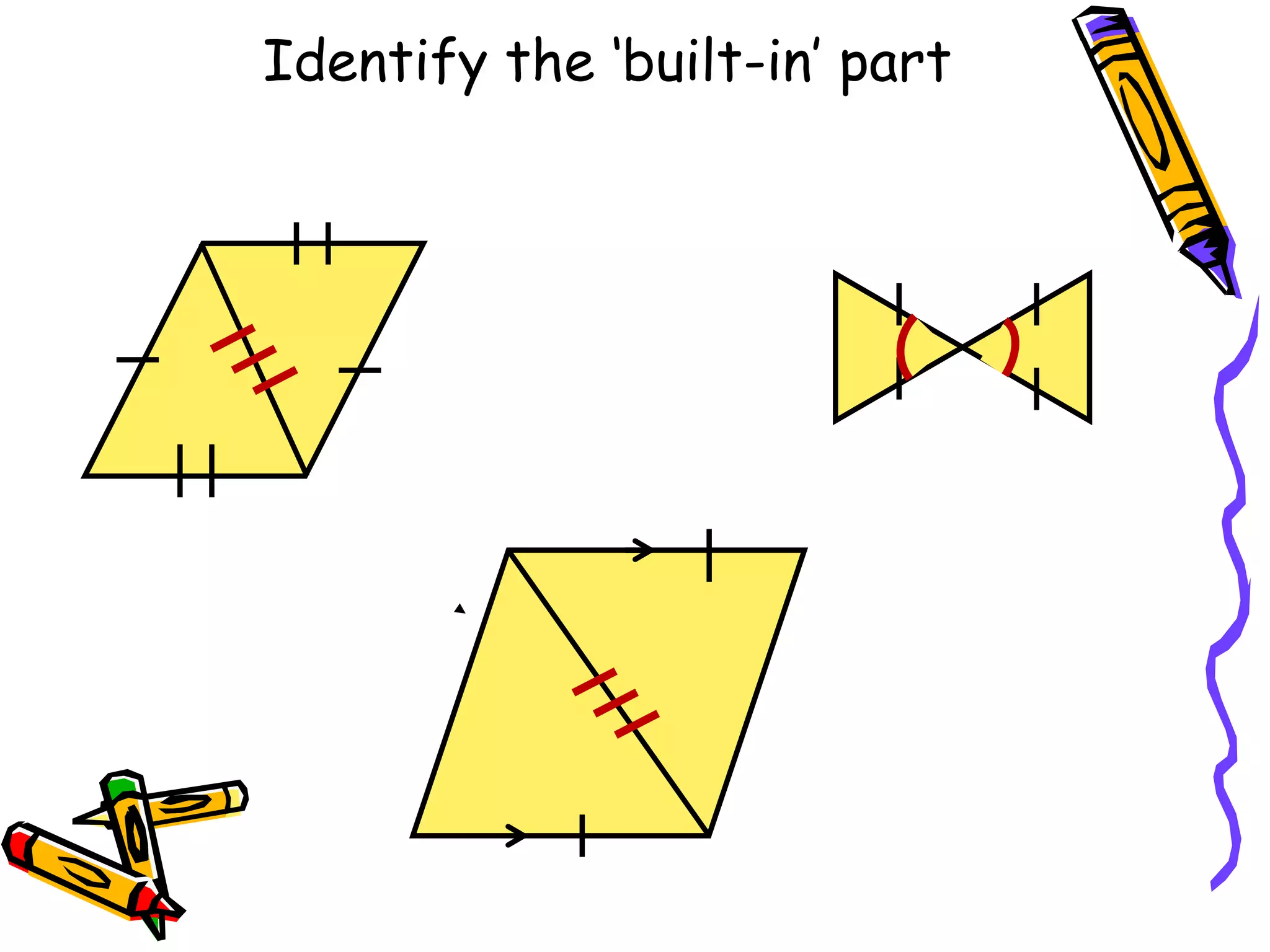
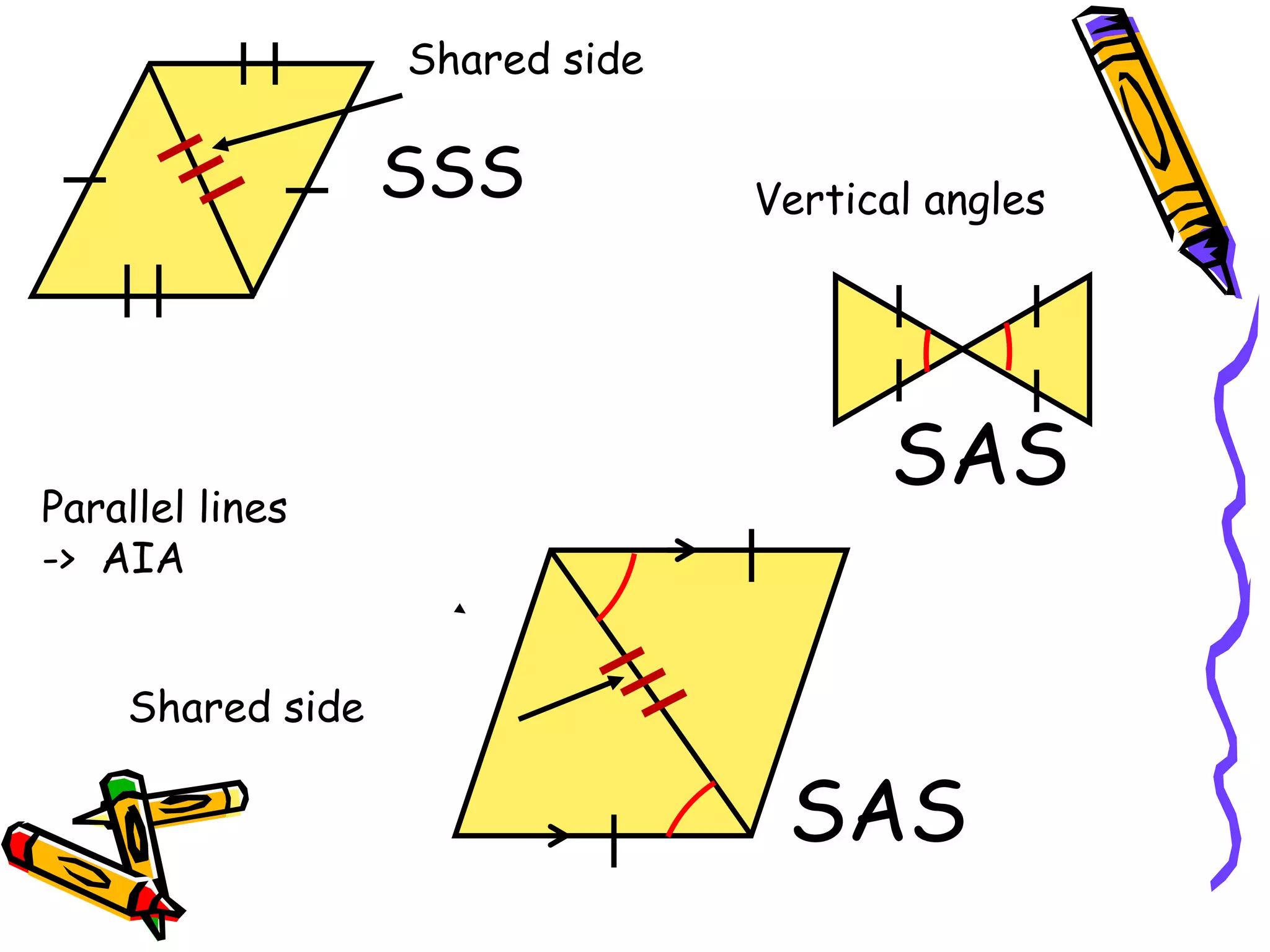
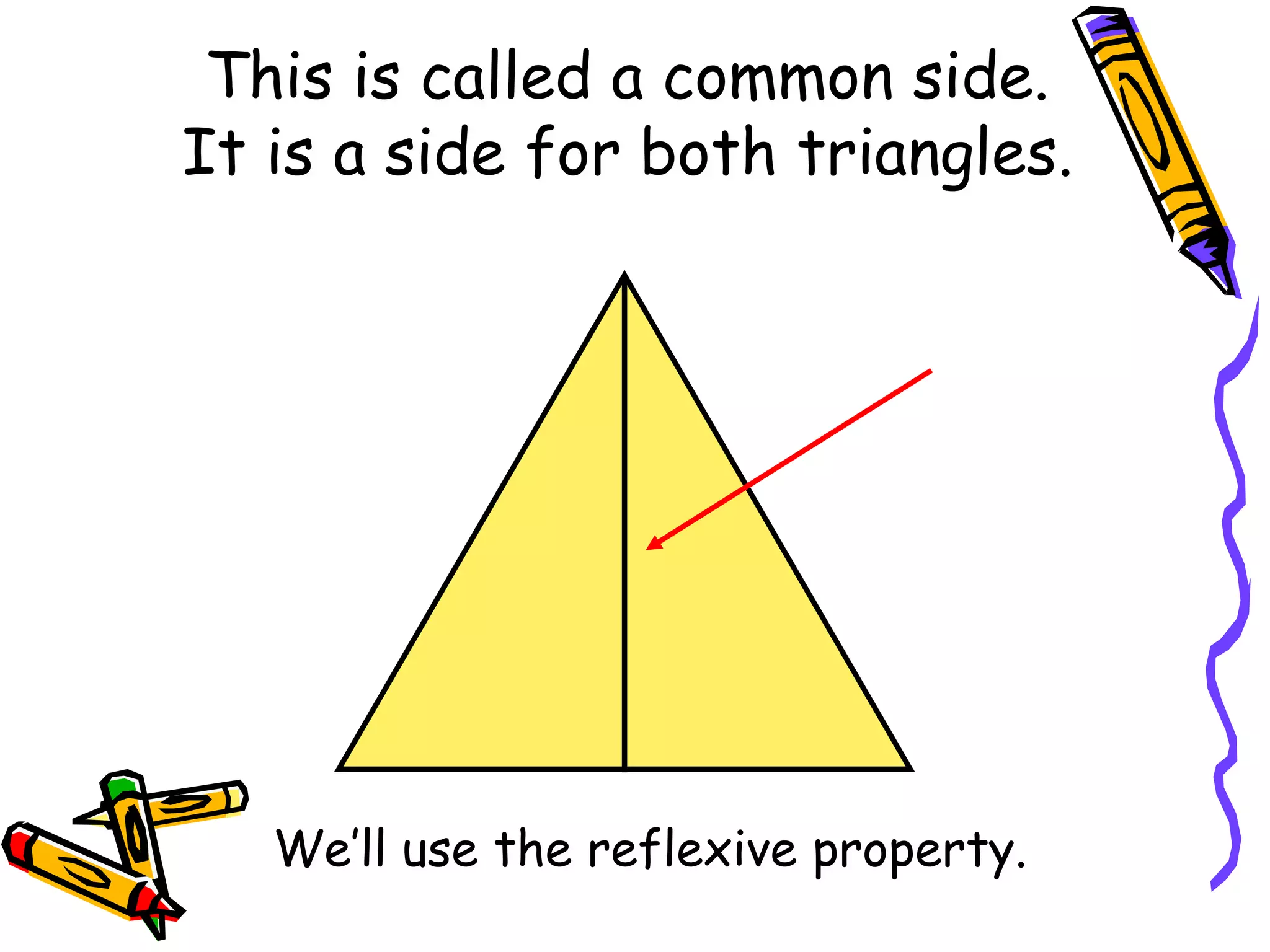
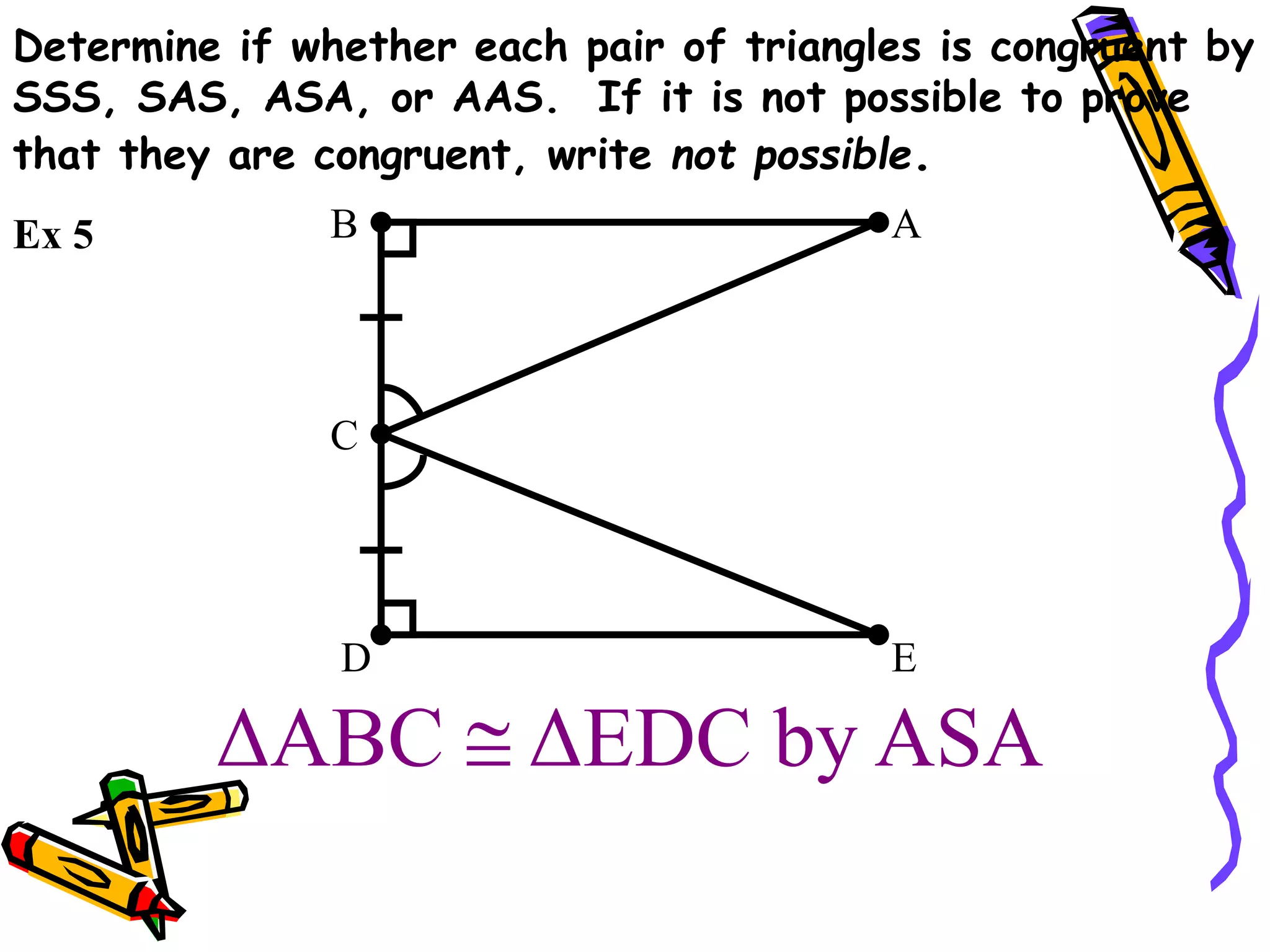
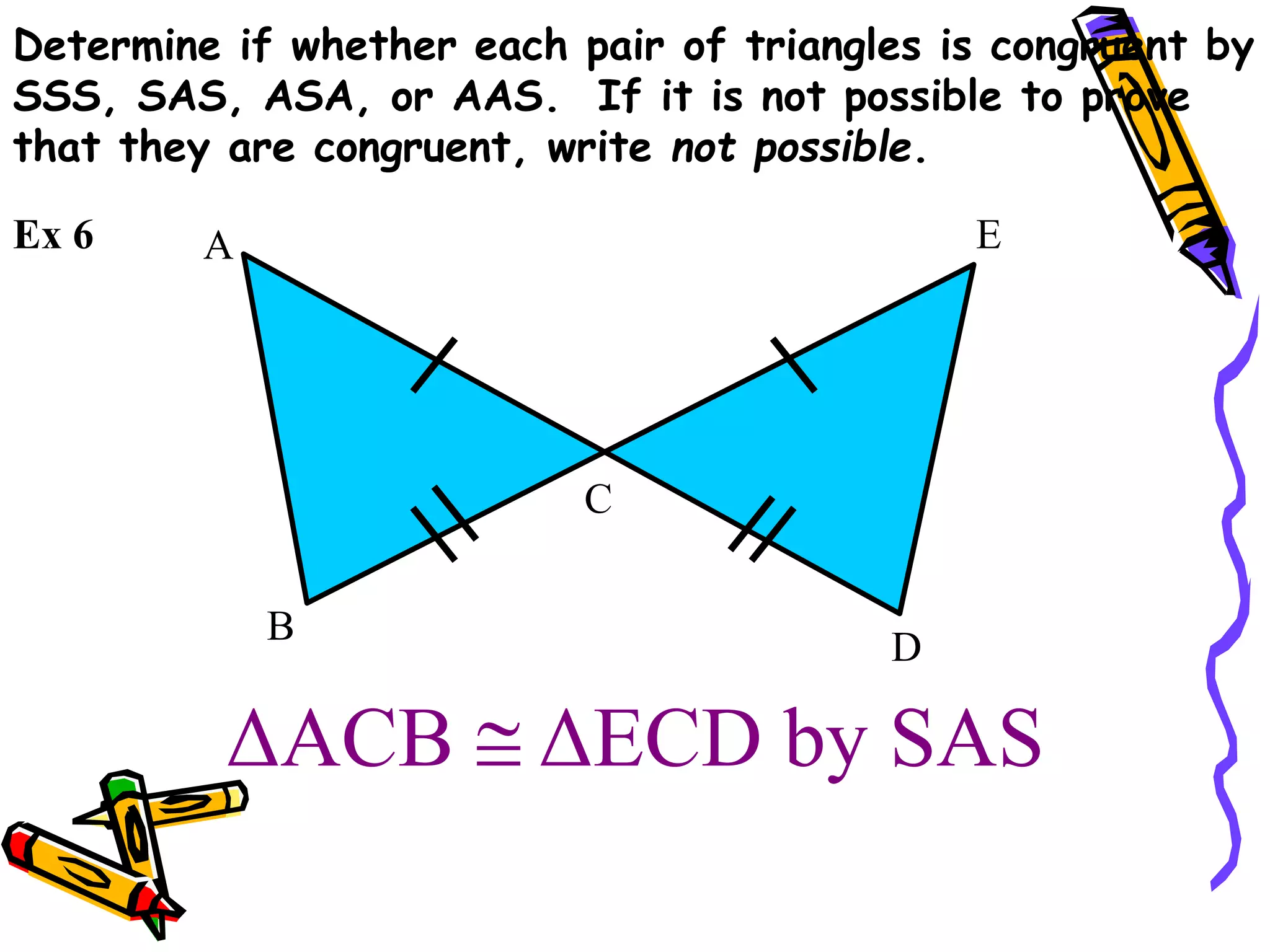
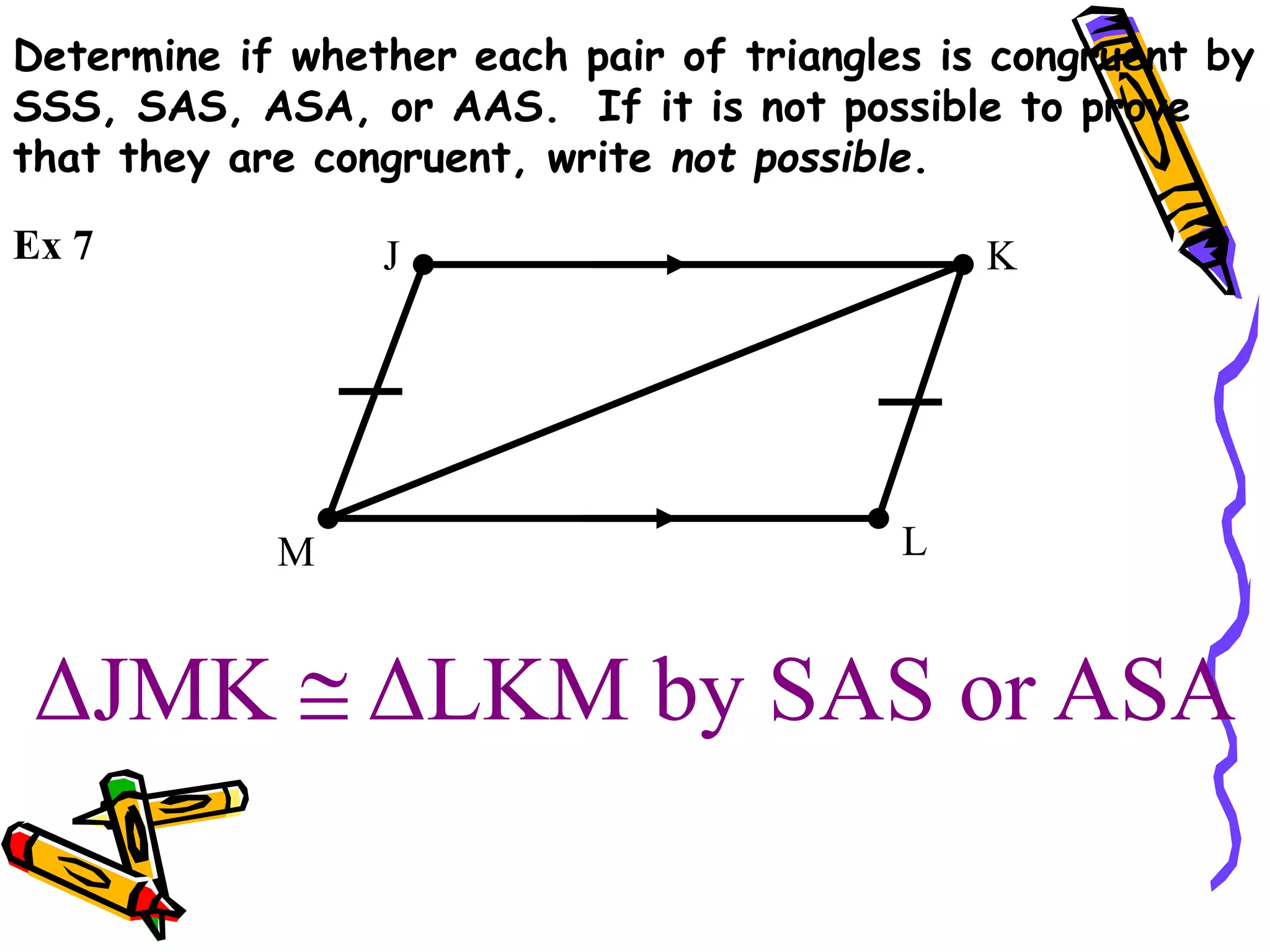
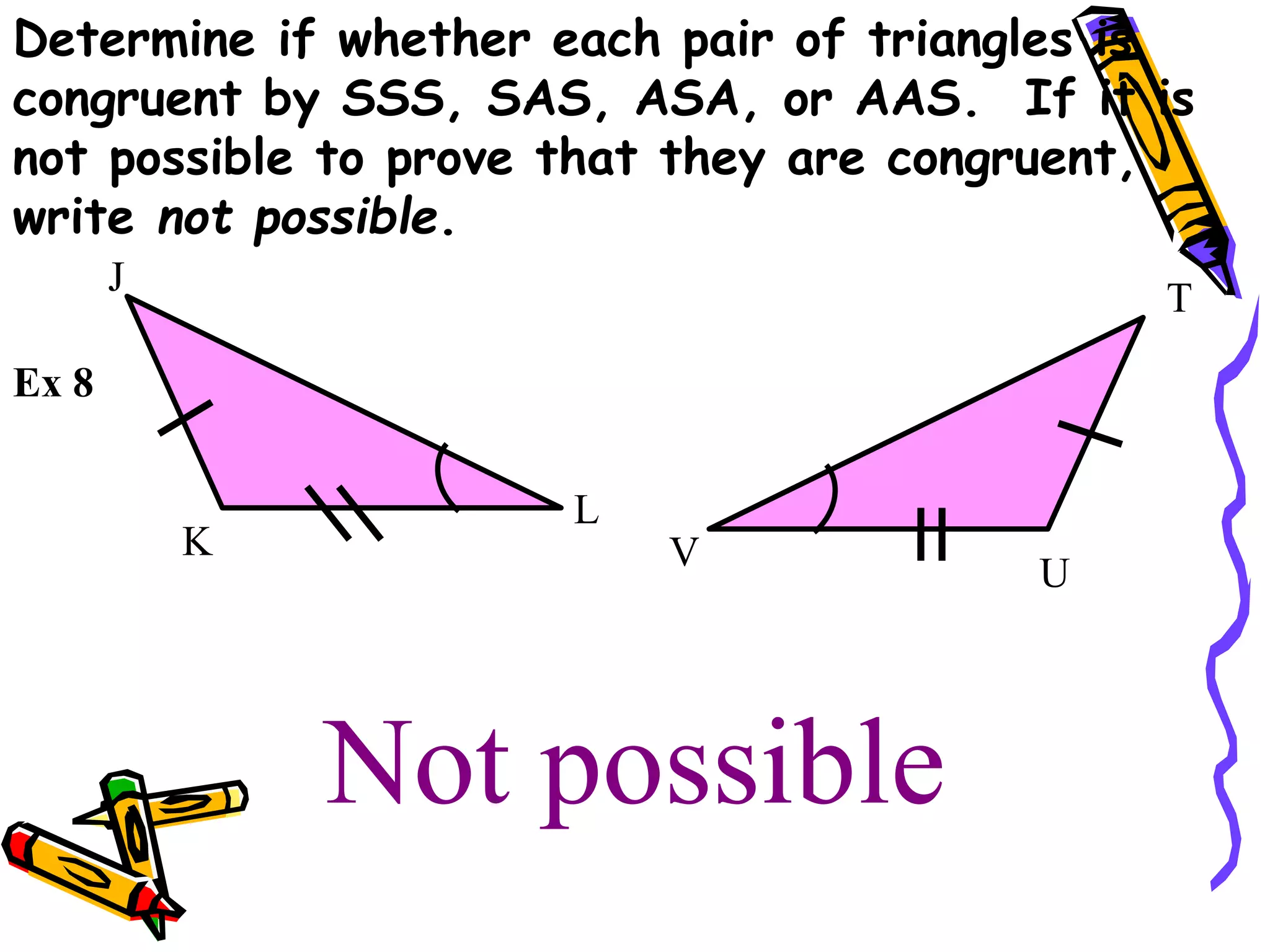
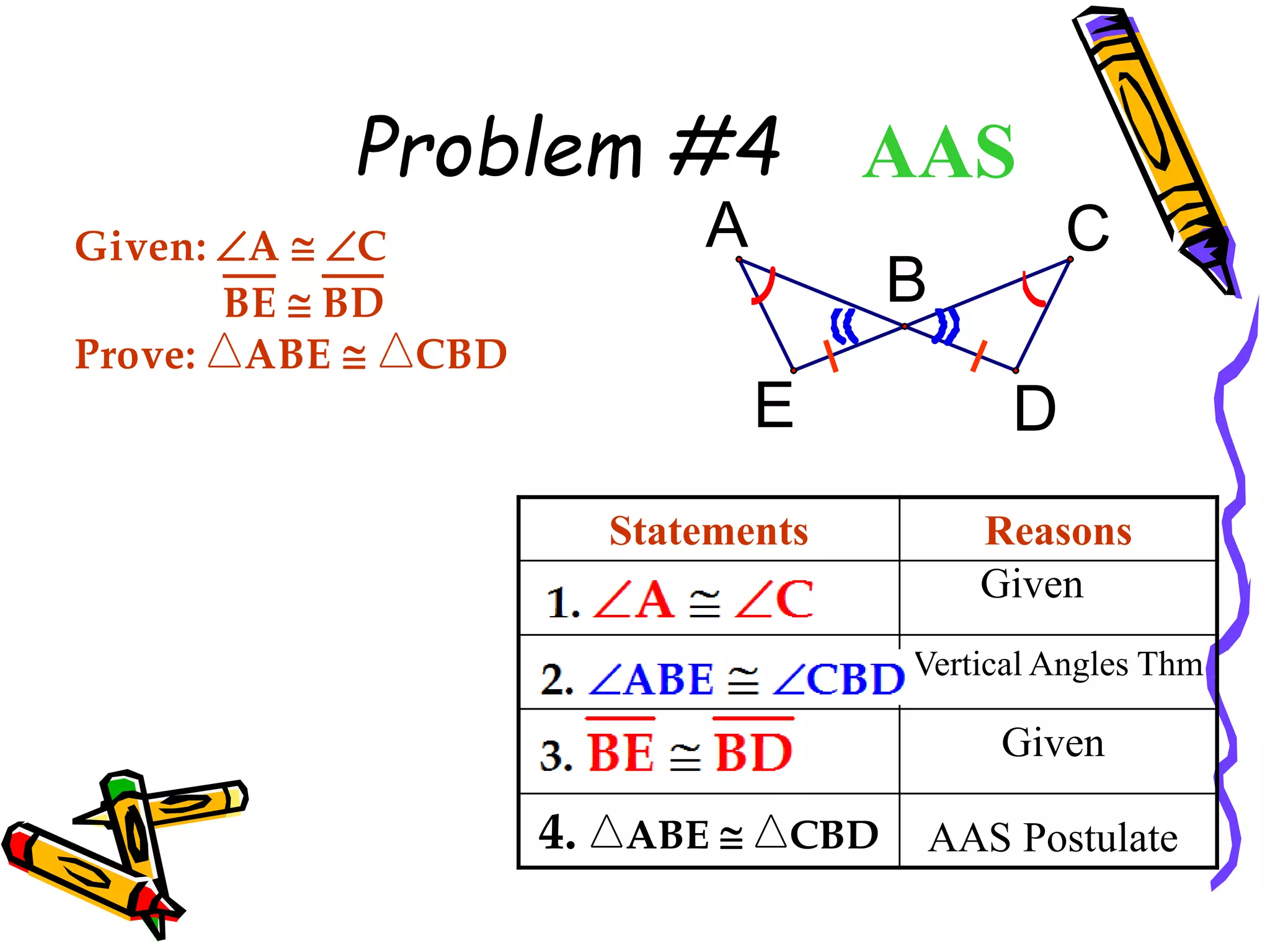
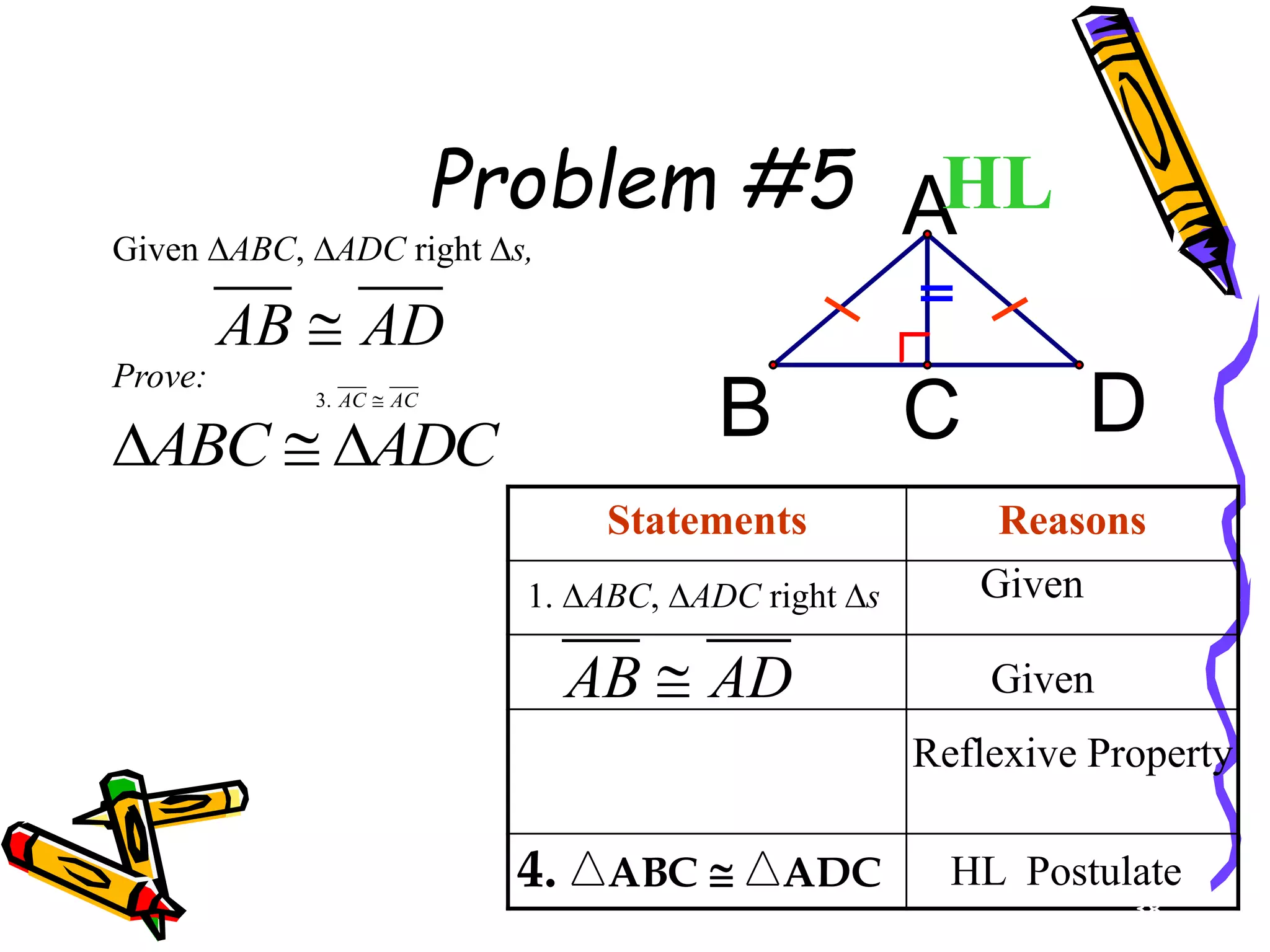
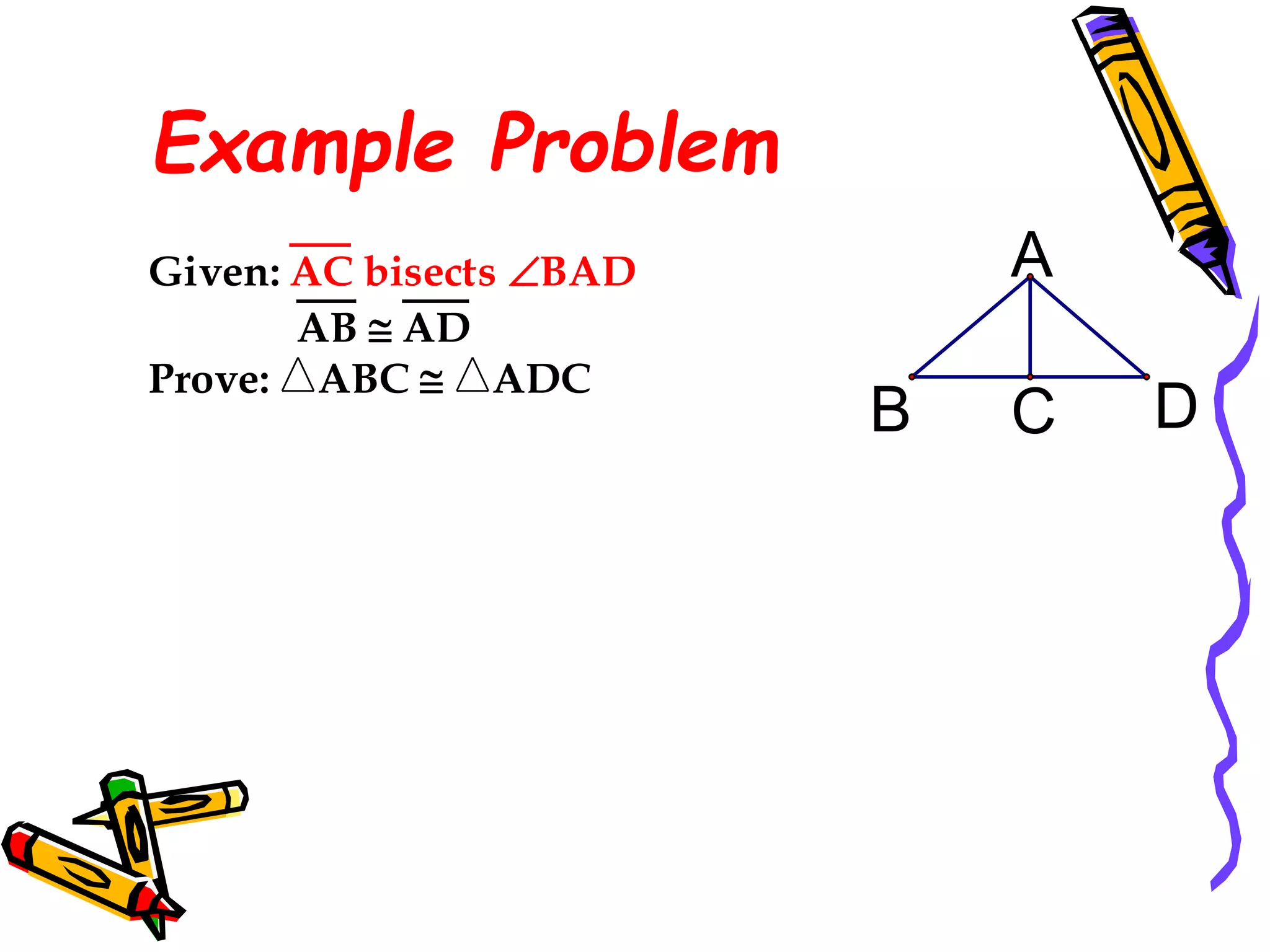
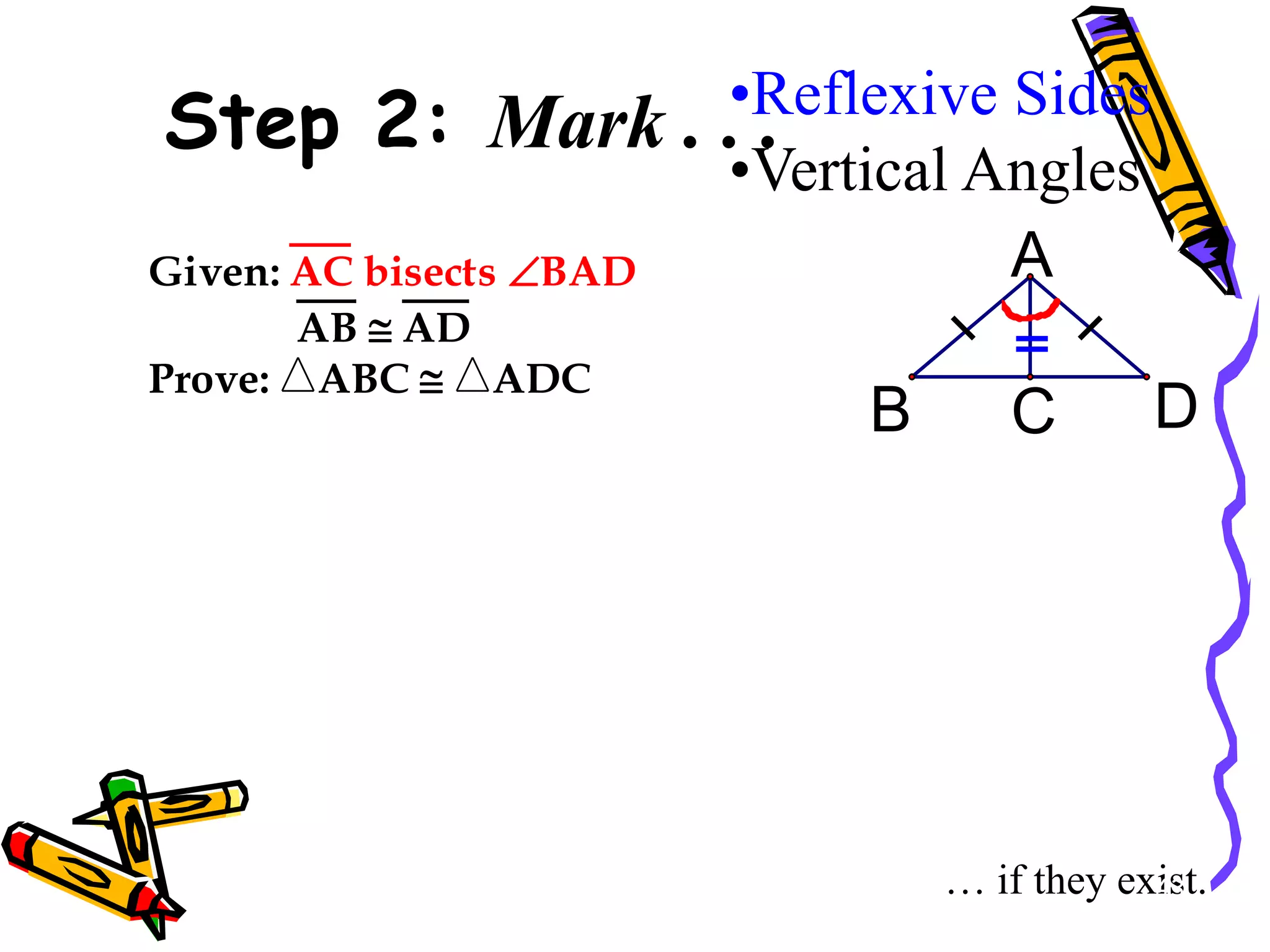
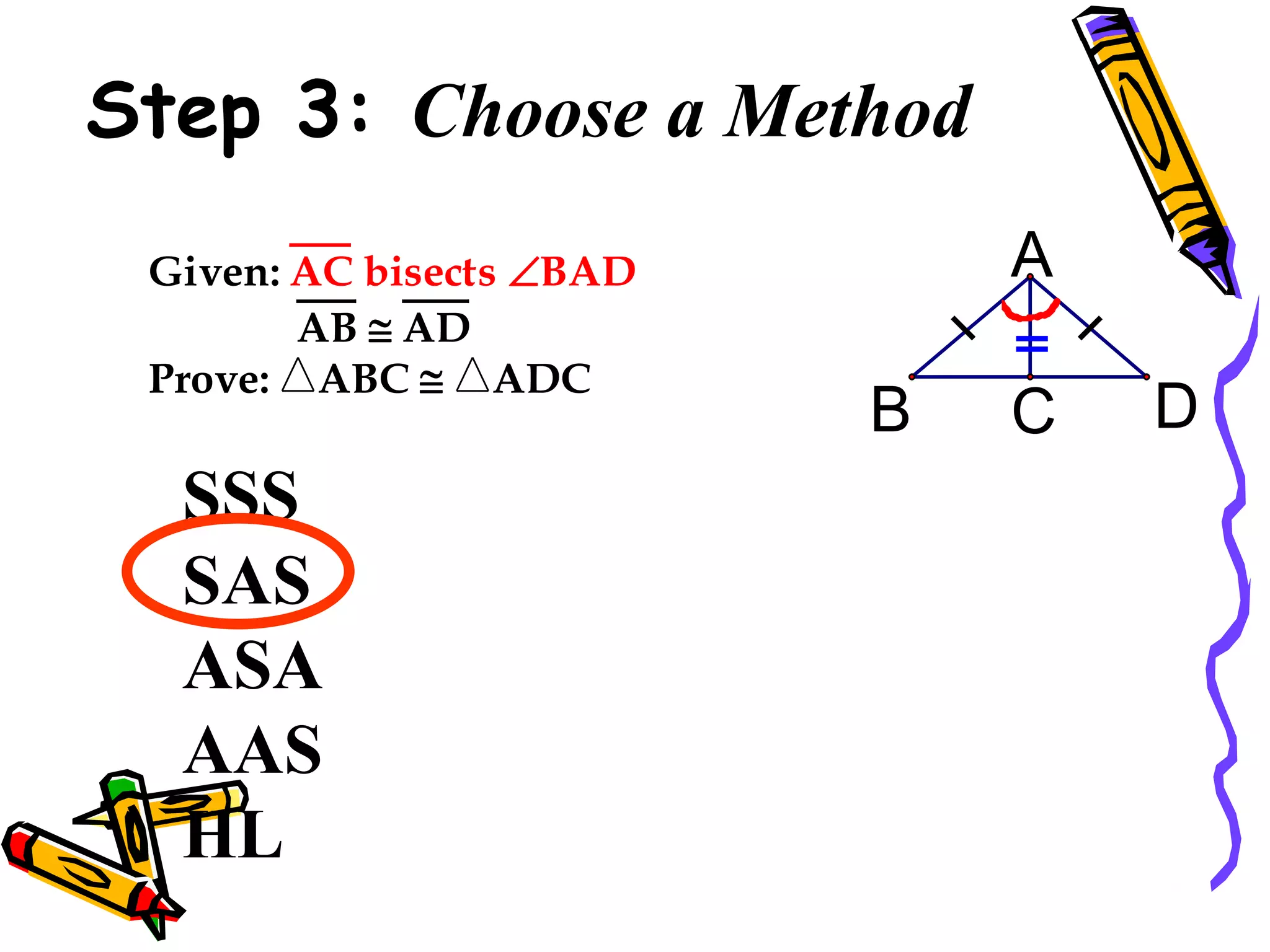
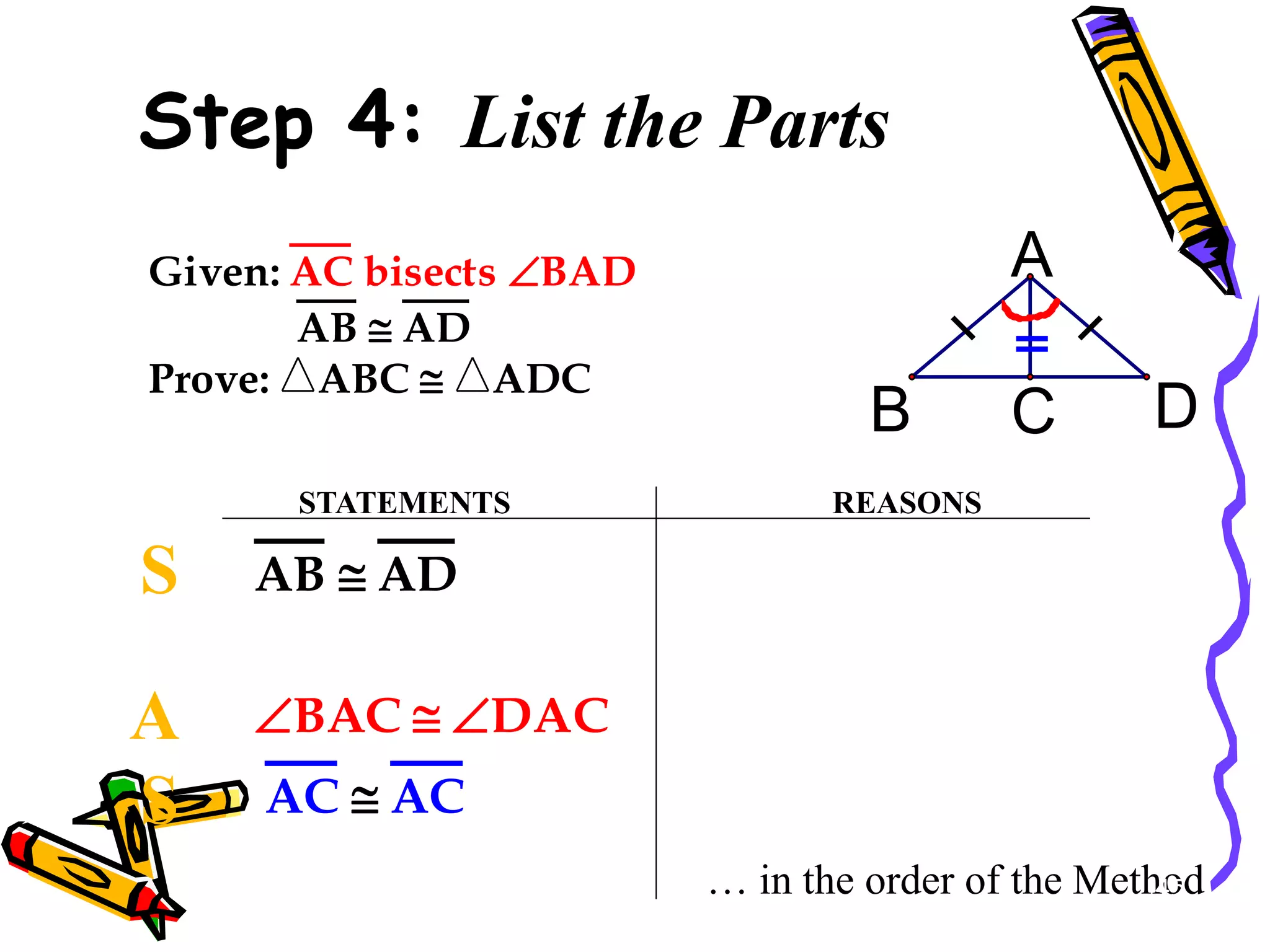
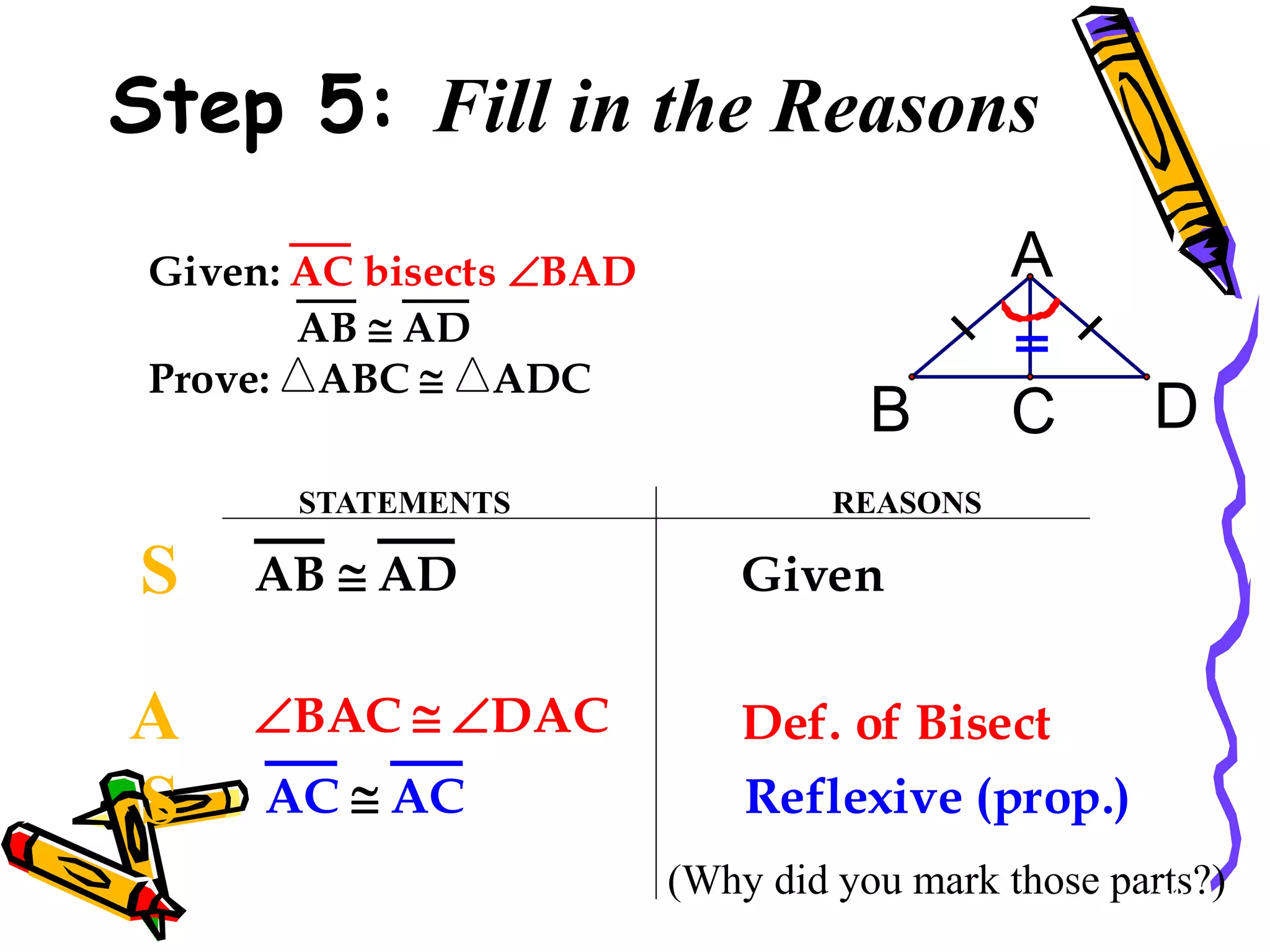
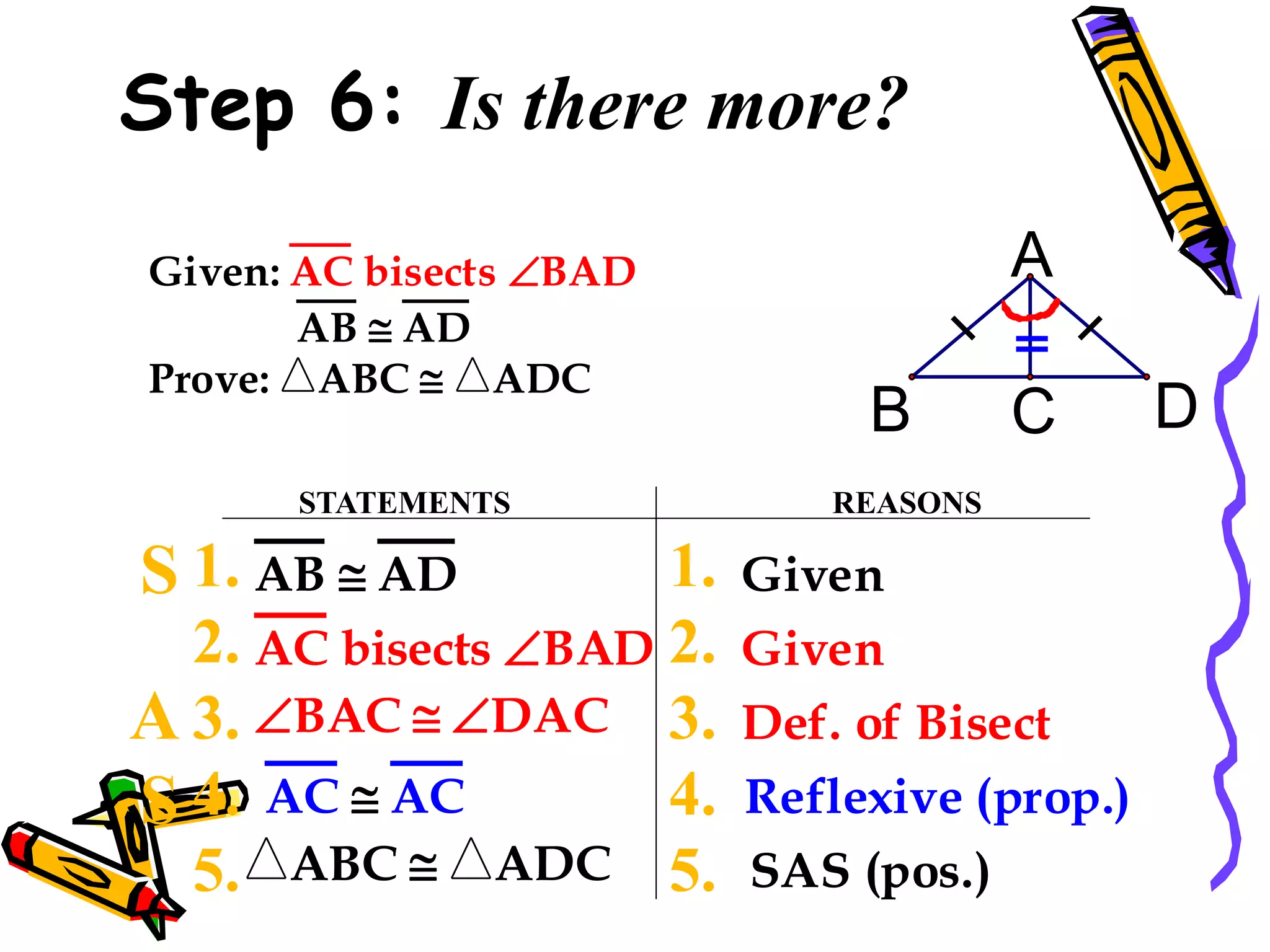
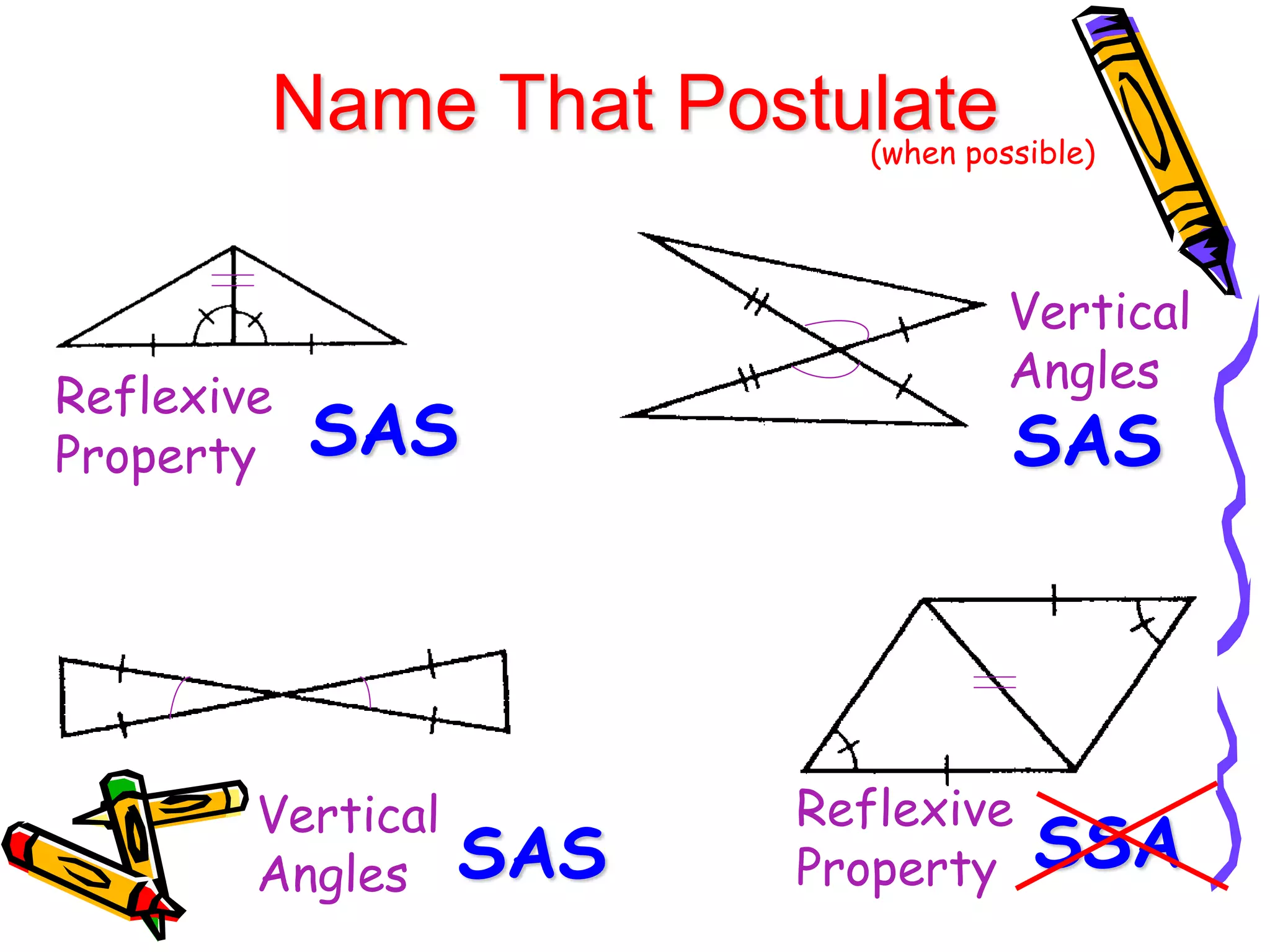
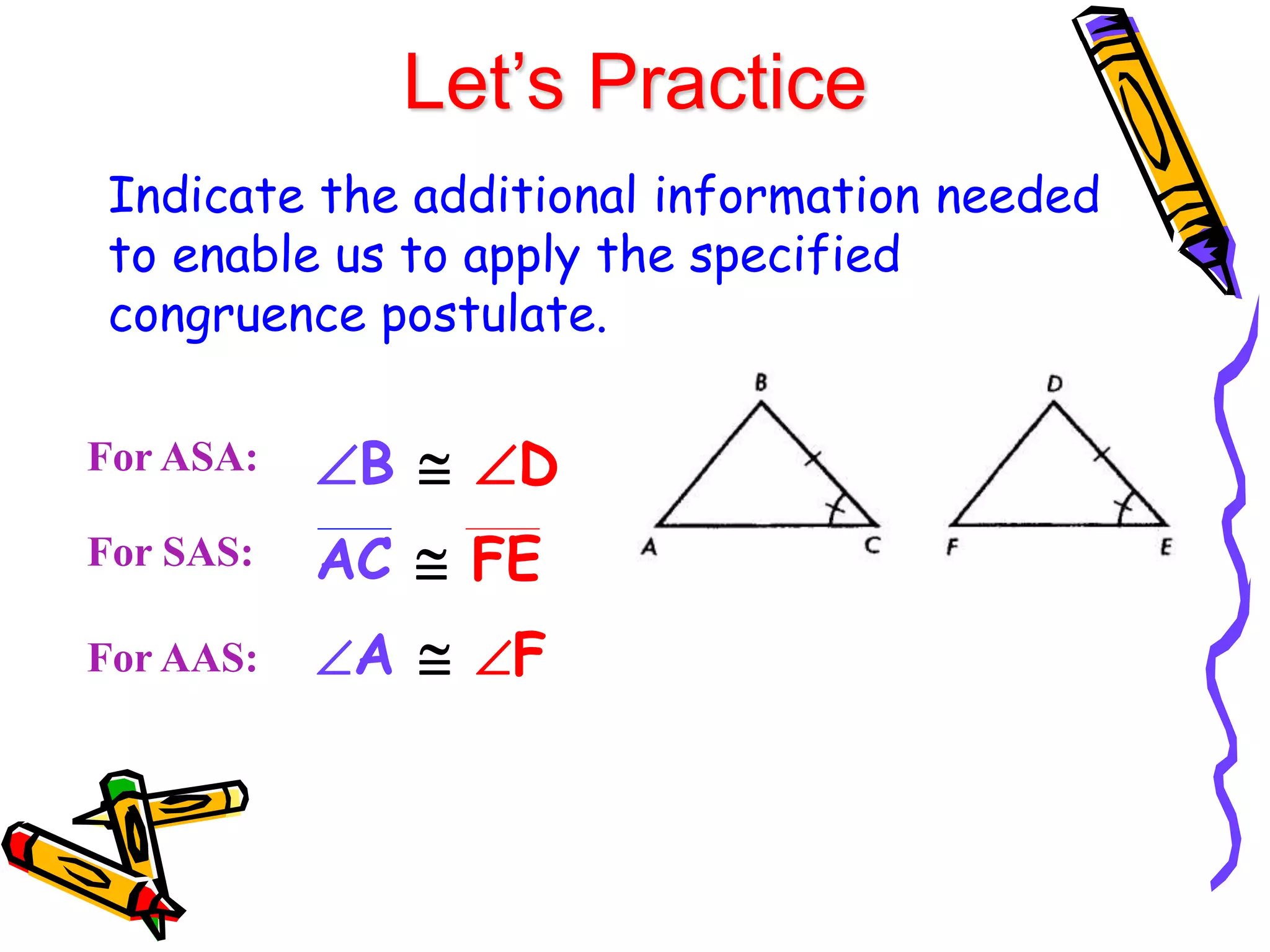
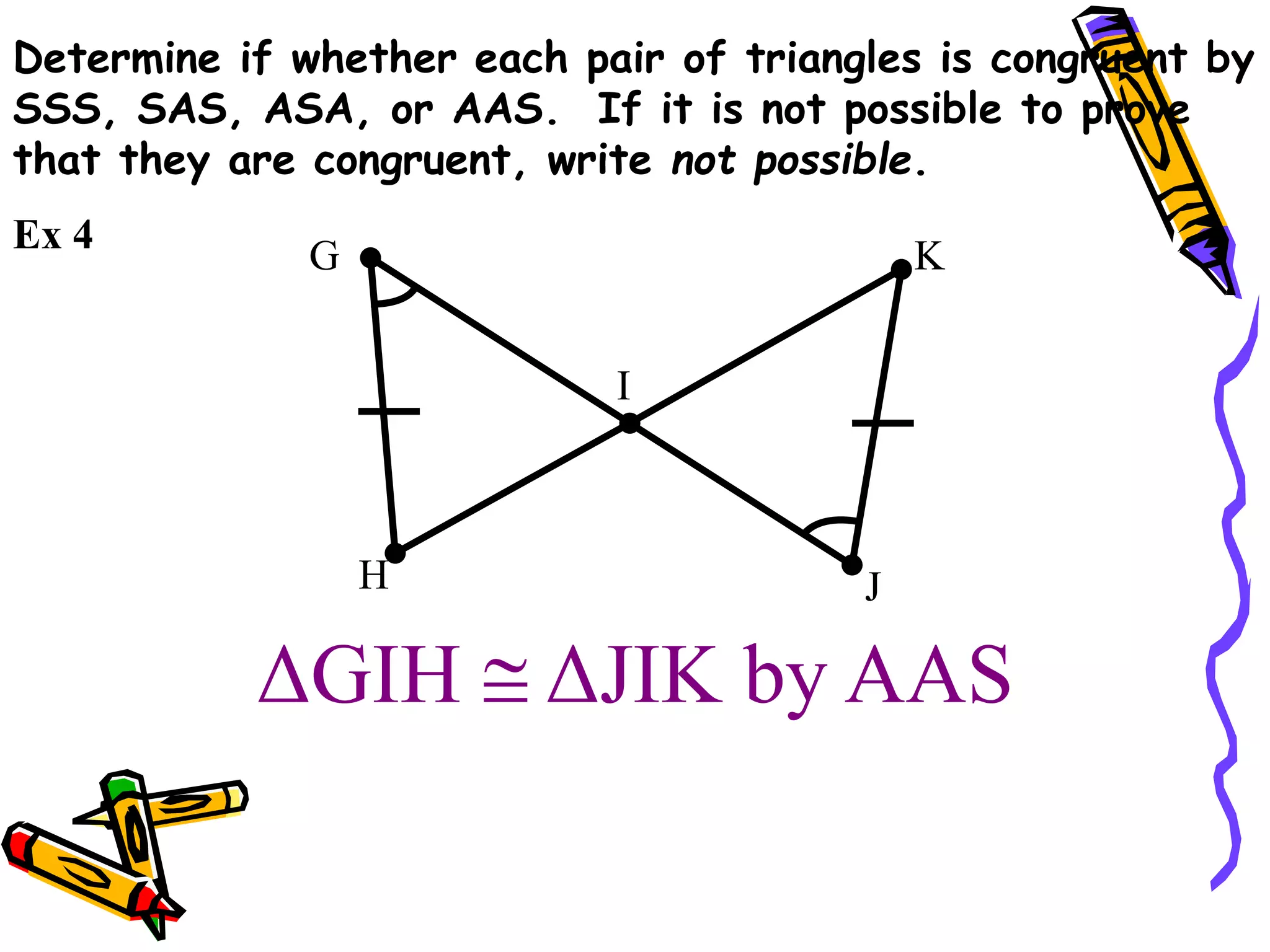
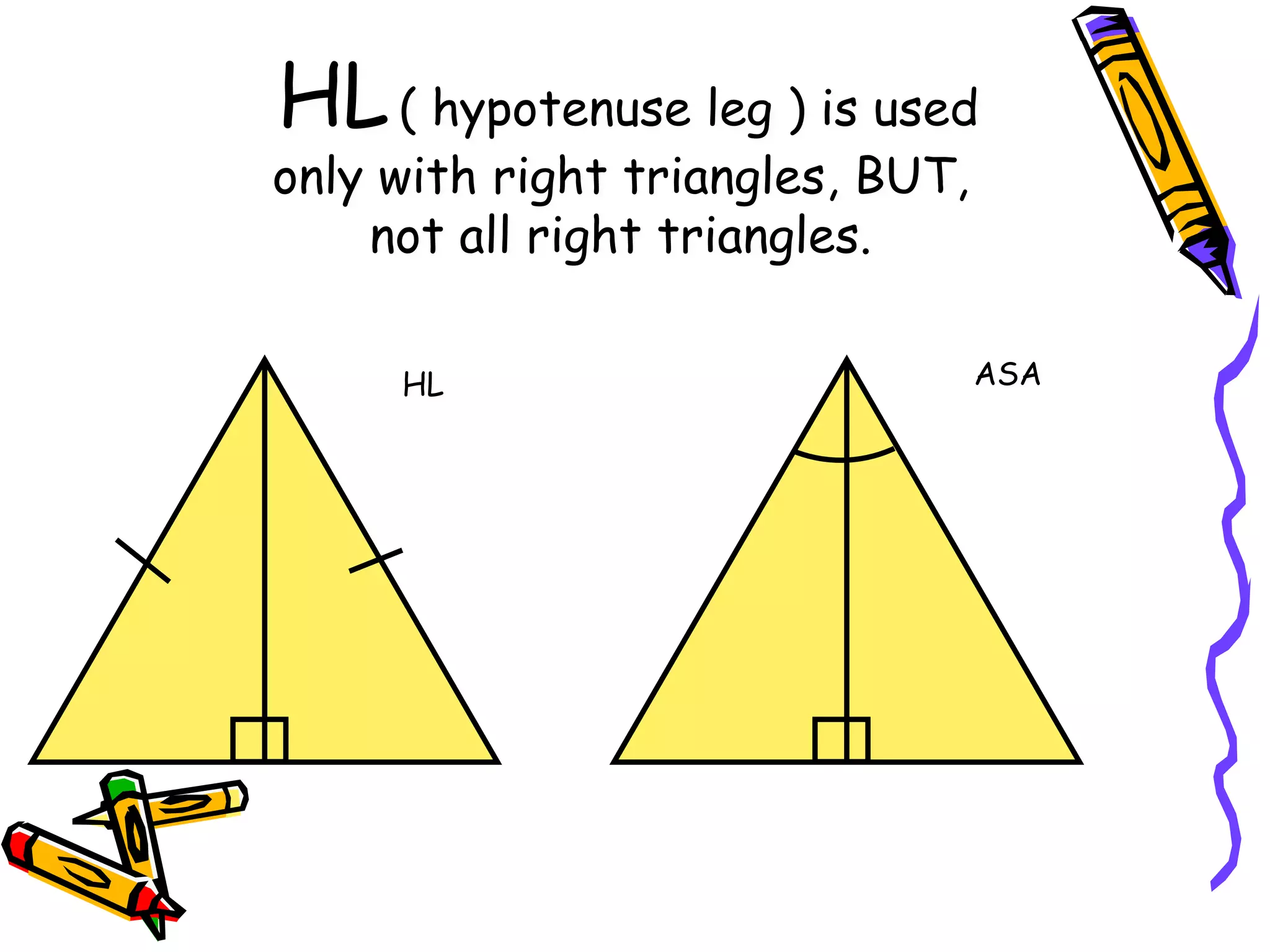
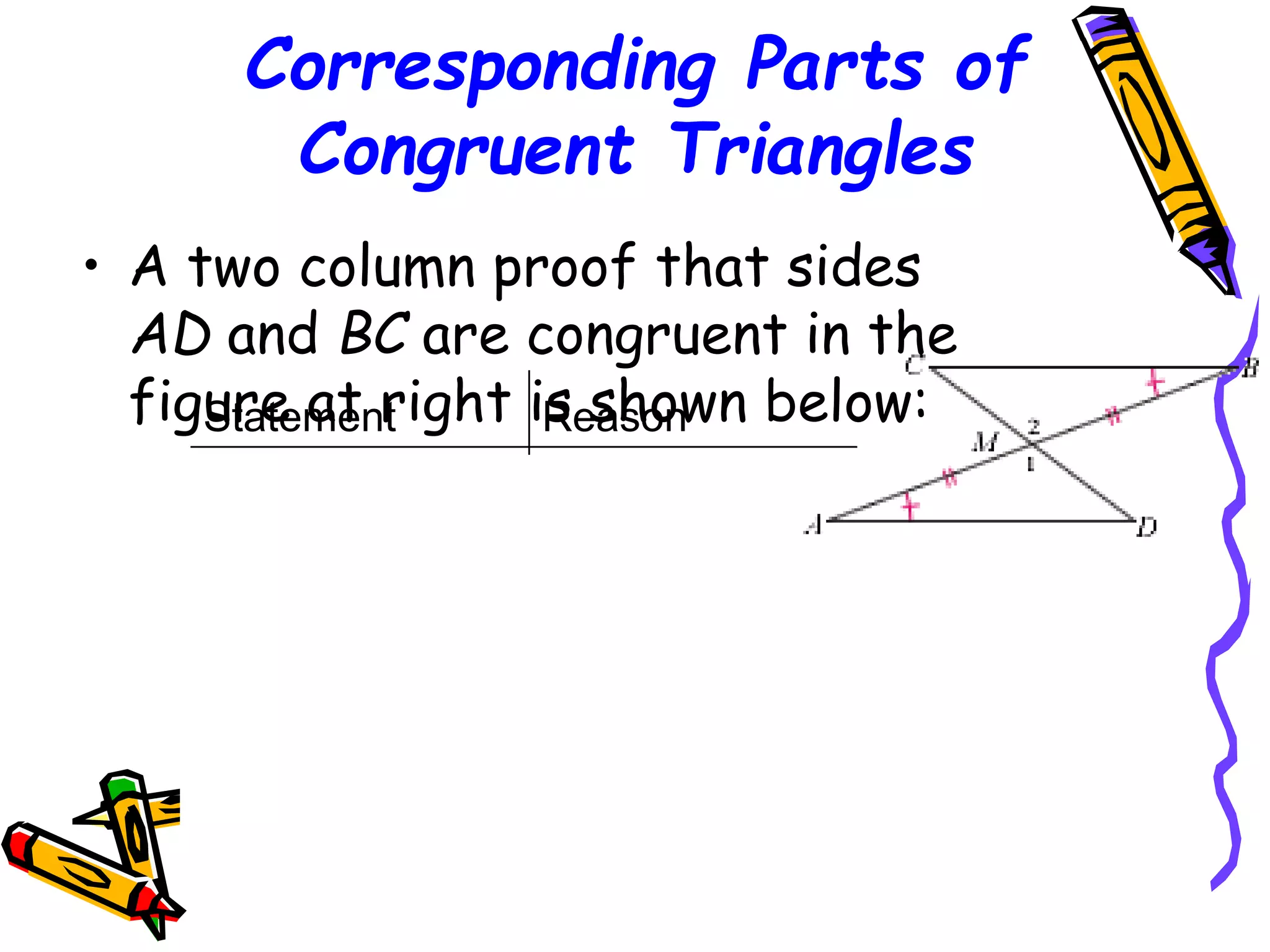
The document discusses different methods for proving triangles congruent: 1. SSS (side-side-side) 2. SAS (side-angle-side) 3. ASA (angle-side-angle) 4. AAS (angle-angle-side) 5. HL (hypotenuse-leg) for right triangles only. It provides examples of using these methods to determine if pairs of triangles are congruent or not. It also discusses using corresponding parts of congruent triangles (CPCTC) to prove additional parts are congruent if two triangles are already shown to be congruent.

1. Proving Triangles
Congruent

2. Triangle Congruency Short-Cuts
If you can prove one of the following short
cuts, you have two congruent triangles
1. SSS (side-side-side)
2. SAS (side-angle-side)
3. ASA (angle-side-angle)
4. AAS (angle-angle-side)
5. HL (hypotenuse-leg) right triangles only!

3. Built – In Information in
Triangles

4. Identify the ‘built-in’ part

5. Shared side
Parallel lines
-> AIA
Shared side
Vertical angles
SAS
SAS
SSS

6. SOME REASONS For Indirect
Information
• Def of midpoint
• Def of a bisector
• Vert angles are congruent
• Def of perpendicular bisector
• Reflexive property (shared side)
• Parallel lines ….. alt int angles
• Property of Perpendicular Lines

7. This is called a common side.
It is a side for both triangles.
We’ll use the reflexive property.

8. HL( hypotenuse leg ) is used
only with right triangles, BUT,
not all right triangles.
HL ASA

9. Name That Postulate
(when possible)
SAS
SAS
SAS
Reflexive
Property
Vertical
Angles
Vertical
Angles
Reflexive
Property SSA

10. Let’s Practice
Indicate the additional information needed
to enable us to apply the specified
congruence postulate.
For ASA:
For SAS:
B  D
For AAS: A  F
AC  FE

11. Determine if whether each pair of triangles is congruent by
SSS, SAS, ASA, or AAS. If it is not possible to prove
that they are congruent, write not possible.
ΔGIH  ΔJIK by AAS
G
I
H J
K
Ex 4

12. ΔABC  ΔEDC by ASA
B A
C
E
D
Ex 5
Determine if whether each pair of triangles is congruent by
SSS, SAS, ASA, or AAS. If it is not possible to prove
that they are congruent, write not possible.

13. ΔACB  ΔECD by SAS
B
A
C
E
D
Ex 6
Determine if whether each pair of triangles is congruent by
SSS, SAS, ASA, or AAS. If it is not possible to prove
that they are congruent, write not possible.

14. ΔJMK  ΔLKM by SAS or ASA
J K
L
M
Ex 7
Determine if whether each pair of triangles is congruent by
SSS, SAS, ASA, or AAS. If it is not possible to prove
that they are congruent, write not possible.

15. Not possible
K
J
L
T
U
Ex 8
Determine if whether each pair of triangles is
congruent by SSS, SAS, ASA, or AAS. If it is
not possible to prove that they are congruent,
write not possible.
V

16. Problem #4
Statements Reasons
AAS
Given
Given
Vertical Angles Thm
AAS Postulate
Given: A  C
BE  BD
Prove: ABE  CBD
E
C
D
A
B
4. ABE  CBD
37

17. Problem #5
3. AC AC

Statements Reasons
C
B D
AHL
Given
Given
Reflexive Property
HL Postulate
4. ABC  ADC
1. ABC, ADC right s
AB AD

Given ABC, ADC right s,
Prove:
AB AD

ABC ADC
  
38

18. Congruence Proofs
1. Mark the Given.
2. Mark …
Reflexive Sides or Angles / Vertical Angles
Also: mark info implied by given info.
3. Choose a Method. (SSS , SAS, ASA)
4. List the Parts …
in the order of the method.
5. Fill in the Reasons …
why you marked the parts.
6. Is there more?
39

19. Given implies Congruent
Parts
midpoint
parallel
segment bisector
angle bisector
perpendicular
segments

angles

segments

angles

angles

40

20. Example Problem
C
B D
A
Given: AC bisects BAD
AB  AD
Prove: ABC  ADC
41

21. Step 1: Mark the Given … and
what it
implies
C
B D
A
Given: AC bisects BAD
AB  AD
Prove: ABC  ADC
42

22. •Reflexive Sides
•Vertical Angles
Step 2: Mark . . .
… if they exist.
C
B D
A
Given: AC bisects BAD
AB  AD
Prove: ABC  ADC
43

23. Step 3: Choose a Method
SSS
SAS
ASA
AAS
HL
C
B D
A
Given: AC bisects BAD
AB  AD
Prove: ABC  ADC
44

24. Step 4: List the Parts
STATEMENTS REASONS
… in the order of the Method
C
B D
A
Given: AC bisects BAD
AB  AD
Prove: ABC  ADC
BAC  DAC
AB  AD
AC  AC
S
A
S
45

25. Step 5: Fill in the Reasons
(Why did you mark those parts?)
STATEMENTS REASONS
C
B D
A
Given: AC bisects BAD
AB  AD
Prove: ABC  ADC
BAC  DAC
AB  AD
AC  AC
Given
Def. of Bisector
Reflexive (prop.)
S
A
S
46

26. S
A
S
Step 6: Is there more?
STATEMENTS REASONS
C
B D
A
Given: AC bisects BAD
AB  AD
Prove: ABC  ADC
BAC  DAC
AB  AD
AC  AC
Given
AC bisects BAD Given
Def. of Bisector
Reflexive (prop.)
ABC  ADC SAS (pos.)
1.
2.
3.
4.
5.
1.
2.
3.
4.
5. 47

27. Congruent Triangles Proofs
1. Mark the Given and what it implies.
2. Mark … Reflexive Sides / Vertical Angles
3. Choose a Method. (SSS , SAS, ASA)
4. List the Parts …
in the order of the method.
5. Fill in the Reasons …
why you marked the parts.
6. Is there more?
53

28. Using CPCTC in Proofs
• According to the definition of congruence, if two
triangles are congruent, their corresponding parts
(sides and angles) are also congruent.
• This means that two sides or angles that are not
marked as congruent can be proven to be congruent
if they are part of two congruent triangles.
• This reasoning, when used to prove congruence, is
abbreviated CPCTC, which stands for
Corresponding Parts of Congruent Triangles are
Congruent.
54

29. Corresponding Parts of
Congruent Triangles
• For example, can you prove that sides AD and BC are
congruent in the figure at right?
• The sides will be congruent if triangle ADM is congruent
to triangle BCM.
– Angles A and B are congruent because they are marked.
– Sides MA and MB are congruent because they are marked.
– Angles 1 and 2 are congruent because they are vertical
angles.
– So triangle ADM is congruent to triangle BCM by ASA.
• This means sides AD and BC are congruent by CPCTC.
55

30. Corresponding Parts of
Congruent Triangles
• A two column proof that sides
AD and BC are congruent in the
figure at right is shown below:
Statement Reason
MA  MB Given
A  B Given
1  2 Vertical angles
ADM  BCM ASA
AD  BC CPCTC
56

31. Corresponding Parts of
Congruent Triangles
• A two column proof that sides
AD and BC are congruent in the
figure at right is shown below:
Statement Reason
MA  MB Given
A  B Given
1  2 Vertical angles
ADM  BCM ASA
AD  BC CPCTC
57

32. Corresponding Parts of
Congruent Triangles
• Sometimes it is necessary to add an
auxiliary line in order to complete a
proof
• For example, to prove ÐR @ ÐO in
this picture
Statement Reason
FR @ FO Given
RU @ OU Given
UF @ UF reflexive prop.
DFRU @ DFOU SSS
ÐR @ ÐO CPCTC
58

33. Corresponding Parts of
Congruent Triangles
• Sometimes it is necessary to add an
auxiliary line in order to complete a
proof
• For example, to prove ÐR @ ÐO in
this picture
Statement Reason
FR @ FO Given
RU @ OU Given
UF @ UF Same segment
DFRU @ DFOU SSS
ÐR @ ÐO CPCTC
59