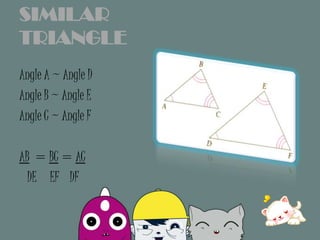
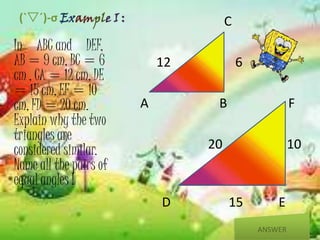
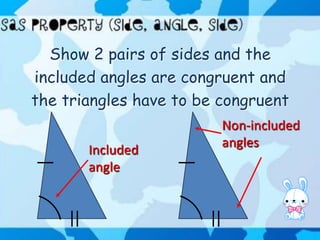
This document discusses similarity and congruence of geometric figures such as rectangles, triangles, and parallelograms. It defines similar figures as those that have the same shape but different sizes, with corresponding sides in proportion. Congruent figures are defined as having the same shape and size, with corresponding angles and sides equal. The document provides examples of proving triangles are similar using corresponding angles and side proportions (AAA), and proving triangles are congruent using corresponding parts (ASA, AAS).

1. SIMILARITY
AND CONGRUENCE

2. Insisivi Eka S
Mutiara Aura K
Sri Ayu Pujiati

3. SIMILARITY
CONGRUENCE

4. SIMILARITY ツ

5. SIMILAR FIGURES
SIMILAR FIGURES

6. SIMILAR FIGURES
Similar figures are two
figures that are the
same shape and whose
sides are proportional

7. ~ This is
the symbol
that means
“similar.”
These figures
are the same
shape but
different
sizes.

9. Example :
A 25 cm x 15 cm rectangle and a 10 cm x 6 cm
rectangle are given. Are the rectangles similar?
15 cm
6cm
10 cm
25 cm

10. ANSWER (≧∇≦)/
The two rectangles have equal corresponding angles
each of which is a right angle.
Ratio of the length = 25 cm : 10 cm = 5 : 2
Ratio of the width = 15 cm : 6 cm = 5 : 2
Thus, Two rectangles are similar . Because the
corresponding angles are equal and the
corresponding sides are proportional.

12. SIMILAR TRIANGLES
Similar
triangles
are two
triangles
that have
the same
shape but
not

13. TWO TRIANGLE ARE SIMILAR IF :
The Corresponding sides are in
proportion
Corresponding pairs of sides
are in proportion

14. SIMILAR
TRIANGLE
Angle A ~ Angle D
Angle B ~ Angle E
Angle C ~ Angle F
AB = BC = AC
DE EF DF

15. Proving
Similarity
(AAA) - Angle,
Angle, Angle
If three angles of one triangle
are congruent, respectively, to
three angles of a second
triangle, then the triangles are
similar.
AAA
AA

16. (`▽´)-σ Example I :
In ABC and DEF,
AB = 9 cm, BC = 6
cm , CA = 12 cm, DE
= 15 cm, EF = 10
cm, FD = 20 cm.
Explain why the two
triangles are
considered similar.
Name all the pairs of
equal angles !
C
12
A
6
B
F
20
D
10
15
E
ANSWER

17. ᾈňšὠὲ ŕ (•"̮•)
In △ABC :
AB = 9 cm
BC = 6 cm
CA = 12 cm
In △ DEF :
DE = 15 cm
EF = 10 cm
FD = 20 cm
AB : DE
= 9 cm : 15 cm
=3:5
BC : EF
= 6 cm : 10 cm
=3:5
CA : FD
= 12 cm : 20 cm
=3:5
Thus, △ABC and △FED are
similar since all the
corresponding sides are
proportional
• The Pairs of equal angles
are :
A=D,B=E, C=F

18. •

19. CONGRUENT
FIGURES
CONGRUENCE
CONGRUENCE
CONGRUENCE
CONGRUENCE
CONGRUENT
TRIANGLES

20. CONGRUENT FIGURES
Two figures are
congruent if
they have same
size and same
shape.

22. The Properties of Two
Congruent Figures
Has same shape and same
size
All corresponding pairs
of angles are congruent
Corresponding pairs of
sides are congruent.

23. D
C
H
G
E
A
B
‘
F

24. Since parallelogram ABCD and EFGH
are congruent :
EH = AB, thus AB = 7 cm
AD = GH , thus AD = 12 cm

26. When we talk about congruent
triangles,
we mean everything about
them Is congruent.
All 3 pairs of corresponding
angles are equal….
And all 3 pairs of corresponding sides are eq

27. Proving Triangles Congruent
• To prove that two triangles are
congruent it is only necessary to
B
show that some corresponding
parts are congruent.
• For example, suppose that in
AB DE
and in
that
and AC
DF
and A
D
C
A
E
• Then intuition tells us that the
remaining sides must be
congruent, and…
• The triangles themselves must be
congruent.
F
D

28. The properties of
congruent
triangle

29. If we can show all 3 pairs of corr.
sides are congruent, the triangles
have to be congruent.

30. Show 2 pairs of sides and the
included angles are congruent and
the triangles have to be congruent
Included
angle
Non-included
angles

31. AAA PROPERTY
(ANGLE,ANGLE, ANGLE)
THIS MEANS WE ARE
GIVEN ALL THREE
ANGLES OF A
TRIANGLE, BUT NO
SIDES.

32. ASA PROPERTY (ANGLE,SIDE, ANGLE)
C
A
F
D
IN TWO TRIANGLES, IF ONE PAIR OF ANGLES
ARE CONGRUENT, ANOTHER PAIR OF ANGLES
ARE CONGRUENT, AND THE PAIR OF SIDES IN
BETWEEN THE PAIRS OF CONGRUENT ANGLES
ARE CONGRUENT, THEN THE TRIANGLES ARE
CONGRUENT.
B
FOR EXAMPLE, IN THE FIGURE, IF THE
CORRESPONDING PARTS ARE CONGRUENT AS
MARKED, THEN
WE CITE “ANGLE-SIDE-ANGLE (ASA)” AS THE
E REASON THE TRIANGLES ARE CONGRUENT.

33. AAS PROPERTY
(ANGLE,ANGLE, SIDE)
C
B
A
F
D
E
In two triangles, if one pair
of angles are congruent,
another pair of angles are
congruent, and a pair of
sides not between the two
angles are congruent, then
the triangles are
congruent.
For example, in the figure,
if the corresponding parts
are congruent as marked,
then

34. THE END