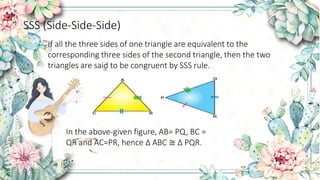
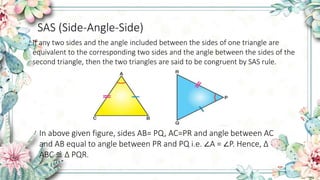
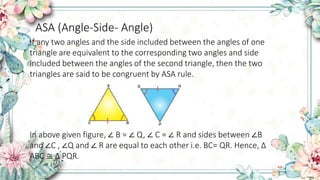
This document discusses different rules for determining if two triangles are congruent: - SSS (Side-Side-Side) rule says two triangles are congruent if all three sides are equal. - SAS (Side-Angle-Side) rule says two triangles are congruent if two sides and the angle between them are equal. - ASA (Angle-Side-Angle) rule says two triangles are congruent if two angles and the side between them are equal. - RHS (Right angle – Hypotenuse – Side) rule says two right triangles are congruent if the hypotenuse and one side are equal.

1. Congruency of
triangle
Reporter：
Christy Praveena
10/11/2022

2. CONTENTS
1 SSS
SSS (Side-Side-Side)
2 SAS
SAS (Side-Angle-Side)
3 ASA
ASA (Angle-Side- Angle)
4 RHS
RHS (Right angle –
Hypotenuse – Side)

3. Congruence of triangles: Two triangles
are said to be congruent if all three
corresponding sides are equal and all the
three corresponding angles are equal in
measure. These triangles can be slides,
rotated, flipped and turned to be looked
identical. If repositioned, they coincide
with each other. The symbol of
congruence is’ ≅’.

4. CPCT is the term, we come across when
we learn about the congruent triangle.
Let’s see the condition for triangles to be
congruent with proof.
CPCT

5. In the above figure, Δ ABC and Δ PQR are congruent triangles. This
means,
Vertices: A and P, B and Q, and C and R are the same.
Sides: AB=PQ, QR= BC and AC=PR;
Angles: ∠A = ∠P, ∠B = ∠Q, and ∠C = ∠R.
Congruent triangles are triangles having corresponding sides and
angles to be equal. Congruence is denoted by the symbol “≅”. From
the above example, we can write ABC ≅ PQR. They have the same area
and the same perimeter.

6. CPCT Full Form
CPCT is the term we come across when we learn about
the congruent triangle. CPCT means “Corresponding
Parts of Congruent Triangles”. As we know that the
corresponding parts of congruent triangles are equal.
While dealing with the concepts related to triangles
and solving questions, we often make use of the
abbreviation cpct in short words instead of full form.

7. SSS (Side-Side-Side)
If all the three sides of one triangle are equivalent to the
corresponding three sides of the second triangle, then the two
triangles are said to be congruent by SSS rule.
In the above-given figure, AB= PQ, BC =
QR and AC=PR, hence Δ ABC ≅ Δ PQR.

8. SAS (Side-Angle-Side)
If any two sides and the angle included between the sides of one triangle are
equivalent to the corresponding two sides and the angle between the sides of the
second triangle, then the two triangles are said to be congruent by SAS rule.
In above given figure, sides AB= PQ, AC=PR and angle between AC
and AB equal to angle between PR and PQ i.e. ∠A = ∠P. Hence, Δ
ABC ≅ Δ PQR.

9. ASA (Angle-Side- Angle)
If any two angles and the side included between the angles of one
triangle are equivalent to the corresponding two angles and side
included between the angles of the second triangle, then the two
triangles are said to be congruent by ASA rule.
In above given figure, ∠ B = ∠ Q, ∠ C = ∠ R and sides between ∠B
and ∠C , ∠Q and ∠ R are equal to each other i.e. BC= QR. Hence, Δ
ABC ≅ Δ PQR.

10. Theorem: In two right-angled triangles, if the length of
the hypotenuse and one side of one triangle, is equal
to the length of the hypotenuse and corresponding
side of the other triangle, then the two triangles are
congruent.
RHS (Right angle – Hypotenuse – Side)

15. Thank you